【算法】KMP-快速文本匹配
文章目录
- 一、KMP算法说明
- 二、详细实现
- 1. next数组定义
- 2. 使用next加速匹配
- 3. next数组如何快速生成
- 4. 时间复杂度O(m+n)的证明
- a) next生成的时间复杂度
- b) 匹配过程时间复杂度
- 三、例题
- 1. [leetcode#572](https://leetcode.cn/problems/subtree-of-another-tree/description/)
- 2. [leetcode#1367](https://leetcode.cn/problems/linked-list-in-binary-tree/description/)
一、KMP算法说明
要判断s1字符串是否包含s2字符串,如果包含返回s1中包含s2的最左开头位置,不包含返回-1
暴力方法就是s1的每个位置都做开头,然后去匹配s2整体,时间复杂度O(n*m),其中n为s1长度,m为s2长度
KMP算法可以做到时间复杂度O(n+m)
二、详细实现
1. next数组定义
字符串s的next数组为int数组,长度等于s的长度。next[i]表示在s中下标i之前子串的前缀和后缀的最大匹配长度(不包含整体)
以字符串"aabaabs"为例
// i=0,规定next[0]为-1
// i=1,由于s[1]之前只有a,除去整体,前缀和后缀只能是空,所以规定next[1]=0
// i=2, "aa",前缀"a",后缀"a",最大匹配长度1,next[2]=1
// i=3, "aab",没有可以匹配的前缀和后缀,next[3]=0
// i=4, "aaba", 前缀"a", 后缀"a", next[4]=1
// i=5, "aabaa", 前缀"aa", 后缀"aa", next[5]=2
// i=6, "aabaab", 前缀"aab", 后缀"aab", next[6]=3
// 扩充的next是可以多计算一位的
// i=7, "aabaabs",没有可以匹配的前缀和后缀,next[7]=0
2. 使用next加速匹配
func kmp(s1, s2 string) int {if len(s1) < len(s2) {return -1}next := nextArr(s2)x, y := 0, 0for x < len(s1) && y < len(s2) {if s1[x] == s2[y] {x++y++} else if y > 0 {y = next[y]} else {x++}}if y == len(s2) {return x - y} else {return -1}
}
3. next数组如何快速生成
func nextArr(s string) []int {if len(s) <= 1 {return []int{-1}}next := make([]int, len(s))next[0], next[1] = -1, 0cp := 0for i := 2; i < len(s); {if s[i-1] == s[cp] {cp++next[i] = cpi++} else if cp > 0 {cp = next[cp]} else {next[i] = 0i++}}return next
}
4. 时间复杂度O(m+n)的证明
a) next生成的时间复杂度
// for循环中我们关注i和i-cp
// i的范围是2~m
// i-cp的范围是0~m
// 分支1:i变大, i-cp不变
// 分支2:i-cp变大
// 分支3:i变大,i-cp变大
// 因此时间复杂度O(m)
b) 匹配过程时间复杂度
// for循环中关注x和x-y
// ...
// 同理时间复杂度O(n)
三、例题
1. leetcode#572
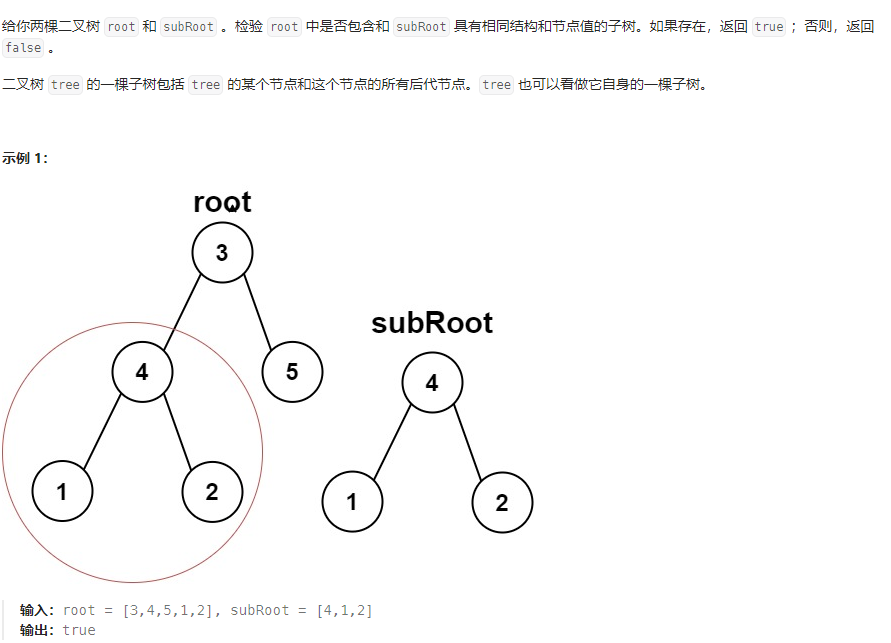
// 思路:将两棵树都序列化为sRoot和sSubRoot,然后判断sSubRoot是否为sRoot的子串func isSubtree(root *TreeNode, subRoot *TreeNode) bool {const nullVal = 1e4 + 1var s1, s2 []ints1 = encode(root, make([]int, 0), nullVal)s2 = encode(subRoot, make([]int, 0), nullVal)return kmp2(s1, s2) >= 0
}
func encode(root *TreeNode, list []int, nullVal int) []int {if root == nil {list = append(list, nullVal)return list}list = append(list, root.Val)list = encode(root.Left, list, nullVal)list = encode(root.Right, list, nullVal)return list
}
func kmp2(s1, s2 []int) int {if len(s1) < len(s2) {return -1}next := nextArrInt(s2)x, y := 0, 0for x < len(s1) && y < len(s2) {if s1[x] == s2[y] {x++y++} else if y > 0 {y = next[y]} else {x++}}if y == len(s2) {return x - y} else {return -1}
}
func nextArrInt(s []int) []int {if len(s) <= 1 {return []int{-1}}next := make([]int, len(s))next[0], next[1] = -1, 0cp := 0for i := 2; i < len(s); {if s[i-1] == s[cp] {cp++next[i] = cpi++} else if cp > 0 {cp = next[cp]} else {next[i] = 0i++}}return next
}2. leetcode#1367

func isSubPath(head *ListNode, root *TreeNode) bool {if head == nil {return true}if root == nil {return false}list := make([]int, 0)for head != nil {list = append(list, head.Val)head = head.Next}next := nextArrInt(list)return find(root, list, next, 0)
}func find(cur *TreeNode, list []int, next []int, index int) bool {if index == len(list) {return true}if cur == nil {return false}for index >= 0 && cur.Val != list[index] {index = next[index]}// index=-1 => index=0// 匹配 => index+1index++return find(cur.Left, list, next, index) || find(cur.Right, list, next, index)
}
相关文章:

【算法】KMP-快速文本匹配
文章目录 一、KMP算法说明二、详细实现1. next数组定义2. 使用next加速匹配3. next数组如何快速生成4. 时间复杂度O(mn)的证明a) next生成的时间复杂度b) 匹配过程时间复杂度 三、例题1. [leetcode#572](https://leetcode.cn/problems/subtree-of-another-tree/description/)2.…...

多维数组和交错数组笔记
1.) 关于数据的几个概念: Rank,即数组的维数,其值是数组类型的方括号之间逗号个数加上1。 Demo:利用一维数组显示斐波那契数列F(n) F(n-1) F(n-2) (n >2 ),每行显示5项,20项. static void Main(string[] args){int[] F n…...

Python(django)之单一接口展示功能前端开发
1、代码 建立apis_manage.html 代码如下: <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>测试平台</title> </head> <body role"document"> <nav c…...

【大模型】非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm
非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm bigdl-llmgithub地址环境安装依赖下载测试模型加载和优化预训练模型使用优化后的模型构建一个聊天应用 bigdl-llm IPEX-LLM is a PyTorch library for running LLM on Intel CPU and GPU (e.g., local P…...

Kubernetes示例yaml:3. service-statefulset.yaml
service-statefulset.yaml 示例 apiVersion: apps/v1 kind: statefulset metadata:...... spec:......volumeMounts:- name: pvcmountPath: /var/lib/arangodb3VolumeClaimTemplates:- metadata:name: pvcspec:accessModes: [ "ReadWriteOnce" ]storangeClassName: …...

Windows平台cmake编译QT源码库,使用VScode开发QT
不愿意安装庞大的QT开发IDE,可以编译QT源码库。 下载源码可以用国内镜像,如清华大学的:Index of /qt/archive/qt/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 我用的是 6.5.3,进去之后,不要下载整个源…...

腾讯云轻量8核16G18M服务器多少钱一年?
腾讯云轻量8核16G18M服务器多少钱一年?优惠价格4224元15个月,买一年送3个月。配置为轻量应用服务器、16核32G28M、28M带宽、6000GB月流量、上海/广州/北京、380GB SSD云硬盘。 腾讯云服务器有两个活动,一个是官方的主会场入口,还…...
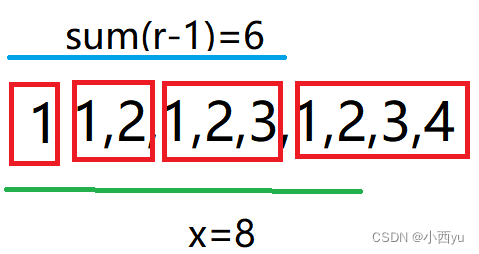
二分练习题——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
淘宝详情数据采集(商品上货,数据分析,属性详情,价格监控),海量数据值得get
淘宝详情数据采集涉及多个环节,包括商品上货、数据分析、属性详情以及价格监控等。在采集这些数据时,尤其是面对海量数据时,需要采取有效的方法和技术来确保数据的准确性和完整性。以下是一些关于淘宝详情数据采集的建议: 请求示…...
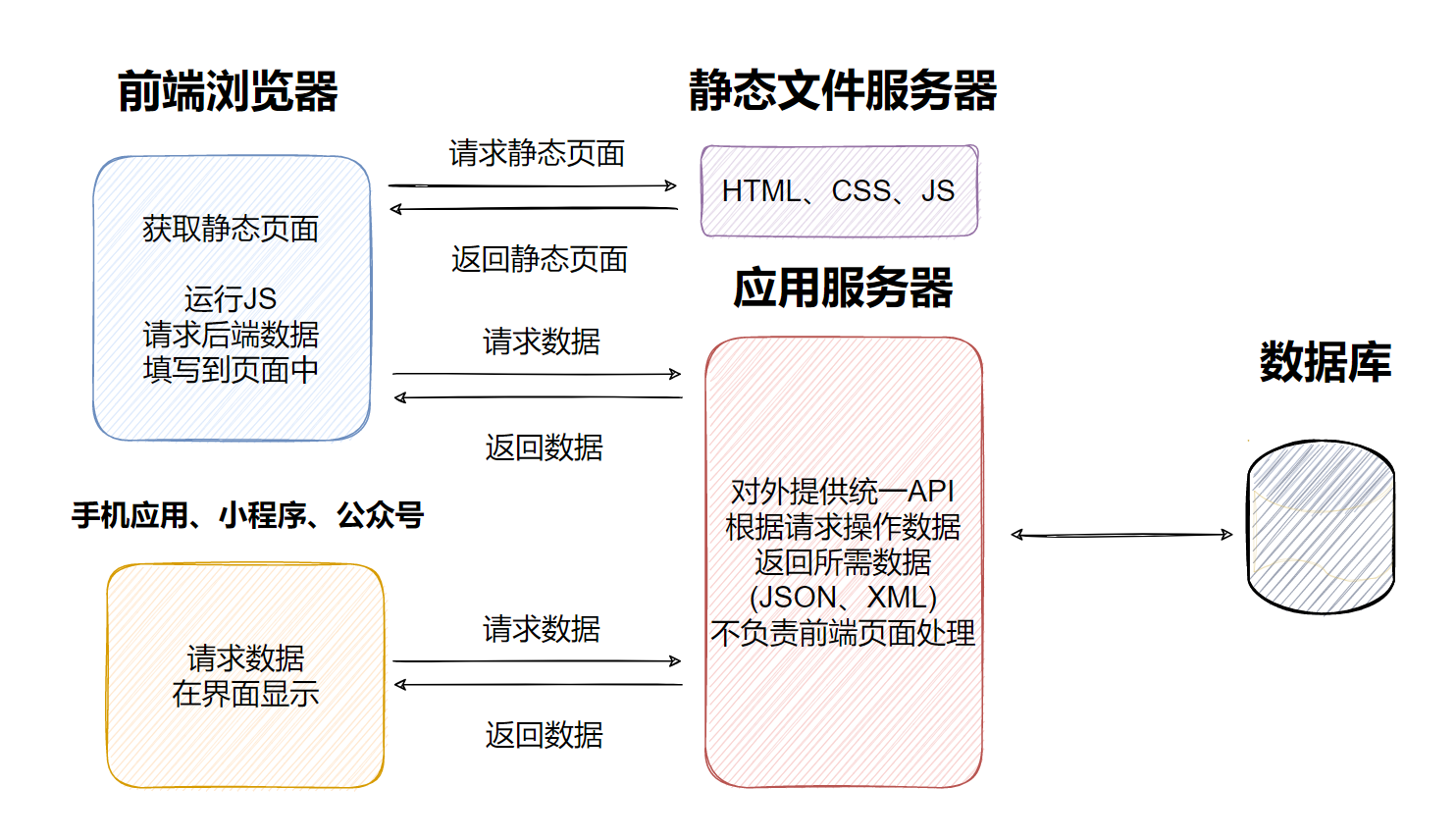
Django之Web应用架构模式
一、Web应用架构模式 在开发Web应用中,有两种模式 1.1、前后端不分离 在前后端不分离的应用模式中,前端页面看到的效果都是由后端控制,由后端渲染页面或重定向,也就是后端需要控制前端的展示。前端与后端的耦合度很高 1.2、前后端分离 在前后端分离的应用模式中,后端仅返…...

GPT提示词分享 —— 口播脚本
可用于撰写视频、直播、播客、分镜头和其他口语内容的脚本。 提示词👇 请以人的口吻,采用缩略语、成语、过渡短语、感叹词、悬垂修饰语和口语化语言,避免重复短语和不自然的句子结构,撰写一篇关于 [主题] 的文章。 GPT3.5&#…...
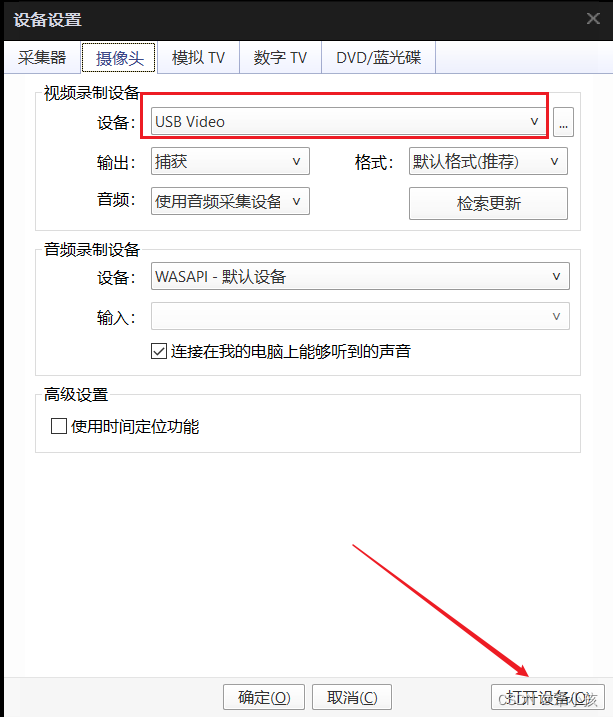
笔记本作为其他主机显示屏(HDMI采集器)
前言: 我打算打笔记本作为显示屏来用,连上工控机,这不是贼方便吗 操作: 一、必需品 HDMI采集器一个 可以去绿联买一个,便宜的就行,我的大概就长这样 win10下载 PotPlayer 软件 下载链接:h…...
02.percona Toolkit工具pt-archiver命令实践
1.命令作用 Percona Toolkit有的32个命令,可以分为7大类 工具类别 工具命令 工具作用 备注 开发类 pt-duplicate-key-checker 列出并删除重复的索引和外键 pt-online-schema-change 在线修改表结构 pt-query-advisor 分析查询语句,并给出建议&#x…...

【天狼启航者】研究计划
“造车”,预计在4月中旬展开(嵌入式蓝桥杯比赛结束后),这里先计划一下,不断更新。 基本要求: 使用STM32F407系列芯片,使用FreeRTOS系统。 驱动程序必须要有强大的可移植性、模块化、低耦合、简…...
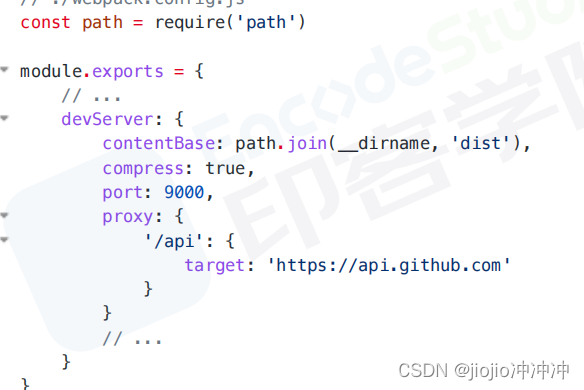
面试题 之 webpack
1.说说你对webpack理解?解决什么问题? Webpack 是实现前端项目的模块化,用于现代 JavaScript 应用程序的静态模块打包工具,被webpack 直接引用的资源打包进 bunde.js的资源,当webpack 处理应用程序时,它会在内部构建一…...

【机器学习之旅】概念启程、步骤前行、分类掌握与实践落地
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...
外星人m18R2国行中文版原厂预装23H2原装Win11系统恢复带F12恢复重置
戴尔外星人m18R2国行中文版原厂预装23H2系统恢复安装 远程恢复安装:https://pan.baidu.com/s/166gtt2okmMmuPUL1Fo3Gpg?pwdm64f 提取码:m64f 1.自带原厂预装系统各驱动,主题,Logo,Office带所有Alienware主题壁纸、Alienware软件驱动 2.带…...
libVLC 视频抓图
Windows操作系统提供了多种便捷的截图方式,常见的有以下几种: 全屏截图:通过按下PrtSc键(Print Screen),可以截取整个屏幕的内容。截取的图像会保存在剪贴板中,可以通过CtrlV粘贴到图片编辑工具…...

Docker搭建LNMP环境实战(06):Docker及Docker-compose常用命令
Docker搭建LNMP环境实战(06):Docker及Docker-compose常用命令 此处列举了docker及docker-compose的常用命令,一方面可以做个了解,另一方面可以在需要的时候进行查阅。不一定要强行记忆,用多了就熟悉了。 1、…...

ClickHouse10-ClickHouse中Kafka表引擎
Kafka表引擎也是一种常见的表引擎,在很多大数据量的场景下,会从源通过Kafka将数据输送到ClickHouse,Kafka作为输送的方式,ClickHouse作为存储引擎与查询引擎,大数据量的数据可以得到快速的、高压缩的存储。 Kafka大家…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
