多维数组和交错数组笔记
1.) 关于数据的几个概念:
Rank,即数组的维数,其值是数组类型的方括号之间逗号个数加上1。
Demo:利用一维数组显示斐波那契数列F(n) = F(n-1) + F(n-2) (n >=2 ),每行显示5项,20项.
static void Main(string[] args){int[] F = new int[20];F[0] = 1;F[1] = 1;//计算斐波那契数列每个元素值for (int i = 2; i < F.Length; i++) F[i] = F[i - 1] + F[i - 2];//循环显示斐波那契数列,每行显示5个for (int i = 0; i < F.Length; i++){//换行if (i >0 && i % 5 == 0)Console.Write("\n");Console.Write(F[i].ToString().PadLeft(6, ' '));}Console.ReadKey();}
2).多维数组
声明多维数组时,用逗号表示维数,一个逗号表示两维数组,两个逗号表示三维数组,以此类推。注意:在声明数组声明中即使没有指定维数的实际大小,也必须使用逗号分隔各个维,如:
//声明一个4行2列的二维数组
int[,] myArray = new int[4, 2];
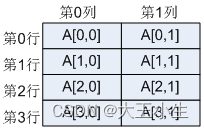
//声明一个3页,5行,2列的3维数组
int[,,] myArray_3 = new int[3, 5, 2];

编程形成并显示4行4列的二维矩形数组
//生成一个4*4的u矩阵int[,] myMatrix = new int[4, 4];int value = 0;for (int r = 0; r < myMatrix.GetLength(0); r++){for (int c = 0; c < myMatrix.GetLength(1); c++){myMatrix[r, c] = value++;Console.Write(value + "\t");if (value % 4 == 0)Console.Write("\n");}}3.)交错数组(jagged array):
数值数组元素的默认值设置为零,而引用元素的默认值设置为 null。
交错数组是数组的数组,因此,它的元素是引用类型,初始化为 null
交错数组元素的维度和大小可以不同,需要声明、实例化并且初始化后才能使用
//定义一个交错数组,有3个元素,然后再给三个元素分别赋值(一维数组)int[][] myJaggedArray = new int[3][];myJaggedArray[0] = new int[]{ 1,2,3,4};myJaggedArray[1] = new int[] { 4, 5,};myJaggedArray[2] = new int[] { 6, 7, 8 };//定义一个交错数组,有3个元素,声明交错数组时初始化一维交错数组的每个元素对应的一维数组int[][] myJaggedArray2 = new int[3][]{new int[]{1,2,3,4},new int[]{4,5},new int[]{6,7,8},};//循环取出交错数组的所有元素并显示出来for (int r = 0; r < myJaggedArray2.Length; r++){//myJaggedArray2[r]元素为一维数组,用Leng属性或GetLeng()方法获取数组长度//对于一维数组GetLength(0)和GetLength(),返回结果一样for (int c = 0; c < myJaggedArray2[r].GetLength(0); c++){Console.Write(myJaggedArray2[r][c] + "\t");}Console.WriteLine();}Console.WriteLine("------------------------------");//声明一个一维交错数组,其元素为大小不同的二维数组int[][,] myJaggedArray3 = new int[3][,]{new int[2,3]{{1,2,3},{4,5,6}},new int[,]{{11,12},{13,14}},new int[,]{{21,22},{ 23, 24},{ 25, 26},{27,28}},};//循环取出交错数组的所有元素并显示出来for (int r = 0; r < myJaggedArray3.Length; r++){//myJaggedArray3[r].GetLength(0)返回一维交错数组第r个元素的0维数组长度,即元素数组的行for (int j = 0; j < myJaggedArray3[r].GetLength(0); j++){//myJaggedArray3[r].GetLength(1)返回一维交错数组第r个元素的1维数组长度,即元素数组的列for (int k = 0; k < myJaggedArray3[r].GetLength(1); k++){Console.Write(myJaggedArray3[r][j, k] + "\t");}Console.WriteLine();}Console.WriteLine();}4.) 数组的基本操作和排序
数据常用操作:数组求和、求平均值、最值及其位置
Array类的常用操作:
Array.clear(数组名,起始元素,元素个数);
Array.Copy(源数组,目标数组,要复制的元素个数);
Array.Copy(源数组,目标数组,目标起始索引,要复制的元素个数);
Array.Reserve(数组名);
Array.Reserve(数组名,起始索引,元素个数);
Array.Sort(数组名);
数组对象的常用操作:
Clone(),CopyTo(),getLength(),GetLowerBound(), GetUpperBound()等方法
Leng,Rank等属性.
数组的常见排序方法,
冒泡法(bubble sort)、选择法(SelectSort);
以10个元素的一维数组升序排序为例,说明冒泡法排序:
将第一个元素与第二个元素比较,如果元素1>元素2,则交换顺序,然后依次每个元素与后面的一个元素比较,大的值往后移,直到9,10元素比较完,第一轮冒泡比较结束
然后开始第二轮,从第二个元素与相邻后面的元素比较,直到比较第8,9元素,
以此类推,比较10-1=9次,就完成了冒泡法升序排列.
选择法就是依次循环选择出最小值,从前往后依次放在的指定位置即可,不再多叙.
相关文章:

多维数组和交错数组笔记
1.) 关于数据的几个概念: Rank,即数组的维数,其值是数组类型的方括号之间逗号个数加上1。 Demo:利用一维数组显示斐波那契数列F(n) F(n-1) F(n-2) (n >2 ),每行显示5项,20项. static void Main(string[] args){int[] F n…...

Python(django)之单一接口展示功能前端开发
1、代码 建立apis_manage.html 代码如下: <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>测试平台</title> </head> <body role"document"> <nav c…...

【大模型】非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm
非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm bigdl-llmgithub地址环境安装依赖下载测试模型加载和优化预训练模型使用优化后的模型构建一个聊天应用 bigdl-llm IPEX-LLM is a PyTorch library for running LLM on Intel CPU and GPU (e.g., local P…...

Kubernetes示例yaml:3. service-statefulset.yaml
service-statefulset.yaml 示例 apiVersion: apps/v1 kind: statefulset metadata:...... spec:......volumeMounts:- name: pvcmountPath: /var/lib/arangodb3VolumeClaimTemplates:- metadata:name: pvcspec:accessModes: [ "ReadWriteOnce" ]storangeClassName: …...

Windows平台cmake编译QT源码库,使用VScode开发QT
不愿意安装庞大的QT开发IDE,可以编译QT源码库。 下载源码可以用国内镜像,如清华大学的:Index of /qt/archive/qt/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 我用的是 6.5.3,进去之后,不要下载整个源…...

腾讯云轻量8核16G18M服务器多少钱一年?
腾讯云轻量8核16G18M服务器多少钱一年?优惠价格4224元15个月,买一年送3个月。配置为轻量应用服务器、16核32G28M、28M带宽、6000GB月流量、上海/广州/北京、380GB SSD云硬盘。 腾讯云服务器有两个活动,一个是官方的主会场入口,还…...
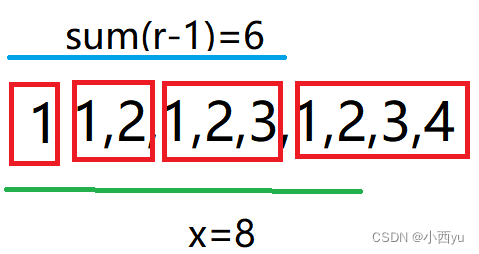
二分练习题——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
淘宝详情数据采集(商品上货,数据分析,属性详情,价格监控),海量数据值得get
淘宝详情数据采集涉及多个环节,包括商品上货、数据分析、属性详情以及价格监控等。在采集这些数据时,尤其是面对海量数据时,需要采取有效的方法和技术来确保数据的准确性和完整性。以下是一些关于淘宝详情数据采集的建议: 请求示…...
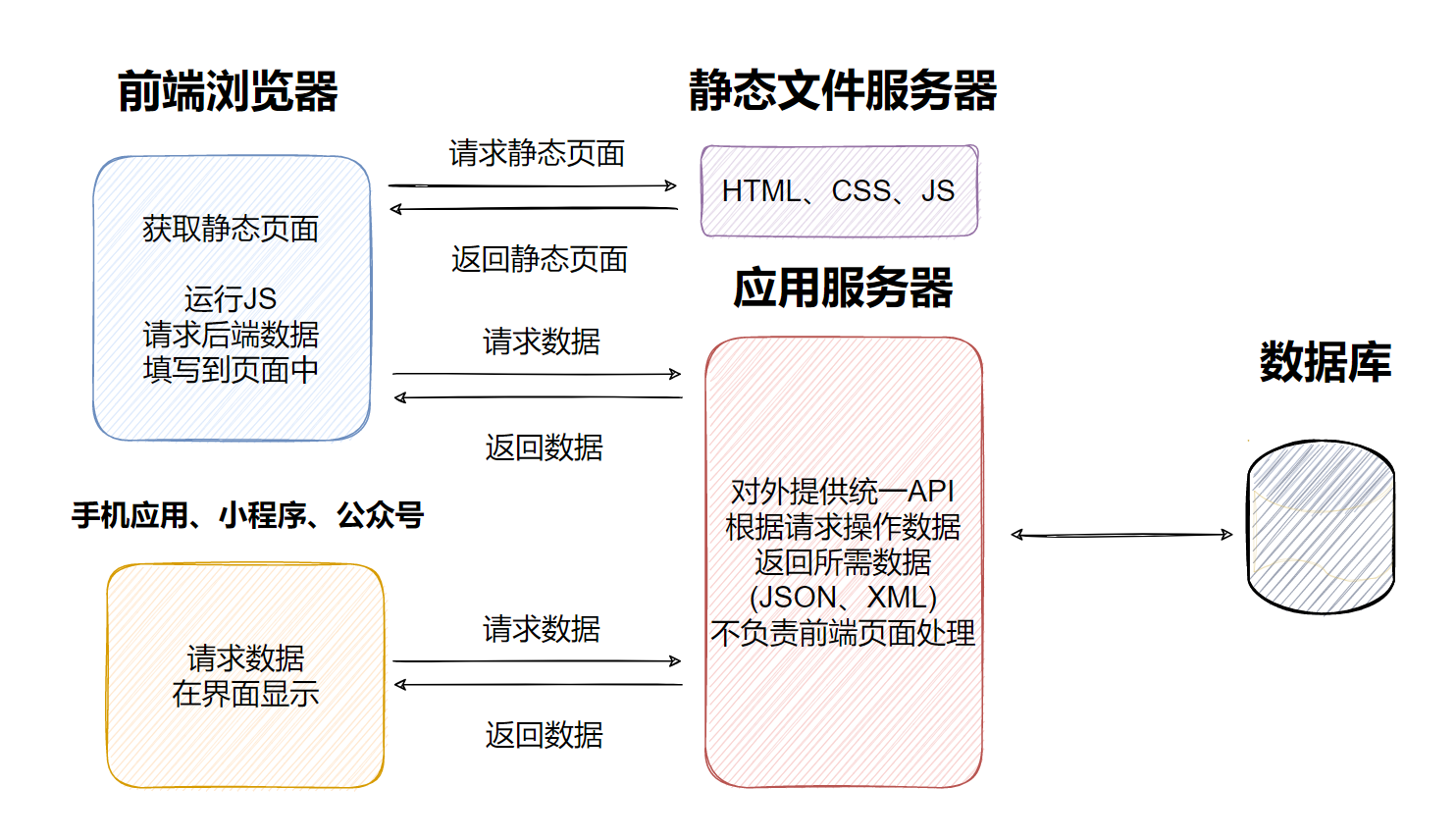
Django之Web应用架构模式
一、Web应用架构模式 在开发Web应用中,有两种模式 1.1、前后端不分离 在前后端不分离的应用模式中,前端页面看到的效果都是由后端控制,由后端渲染页面或重定向,也就是后端需要控制前端的展示。前端与后端的耦合度很高 1.2、前后端分离 在前后端分离的应用模式中,后端仅返…...

GPT提示词分享 —— 口播脚本
可用于撰写视频、直播、播客、分镜头和其他口语内容的脚本。 提示词👇 请以人的口吻,采用缩略语、成语、过渡短语、感叹词、悬垂修饰语和口语化语言,避免重复短语和不自然的句子结构,撰写一篇关于 [主题] 的文章。 GPT3.5&#…...
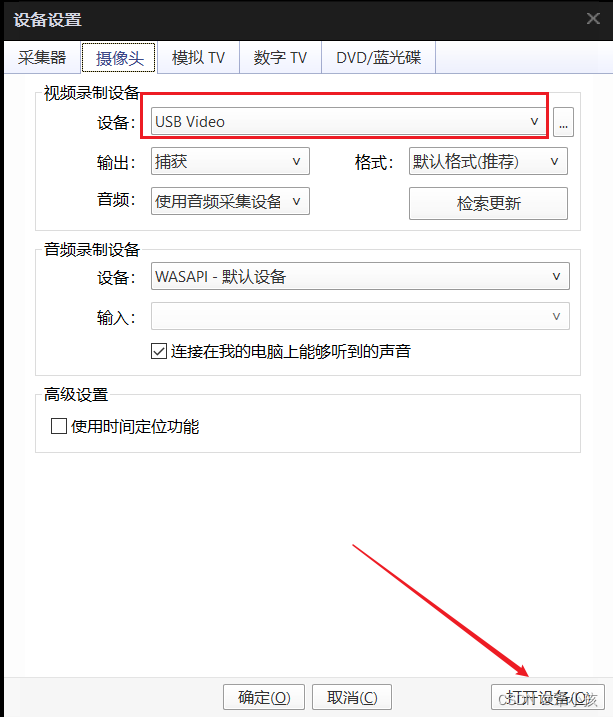
笔记本作为其他主机显示屏(HDMI采集器)
前言: 我打算打笔记本作为显示屏来用,连上工控机,这不是贼方便吗 操作: 一、必需品 HDMI采集器一个 可以去绿联买一个,便宜的就行,我的大概就长这样 win10下载 PotPlayer 软件 下载链接:h…...
02.percona Toolkit工具pt-archiver命令实践
1.命令作用 Percona Toolkit有的32个命令,可以分为7大类 工具类别 工具命令 工具作用 备注 开发类 pt-duplicate-key-checker 列出并删除重复的索引和外键 pt-online-schema-change 在线修改表结构 pt-query-advisor 分析查询语句,并给出建议&#x…...

【天狼启航者】研究计划
“造车”,预计在4月中旬展开(嵌入式蓝桥杯比赛结束后),这里先计划一下,不断更新。 基本要求: 使用STM32F407系列芯片,使用FreeRTOS系统。 驱动程序必须要有强大的可移植性、模块化、低耦合、简…...
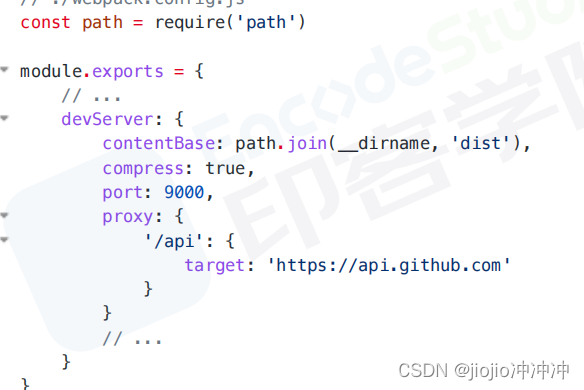
面试题 之 webpack
1.说说你对webpack理解?解决什么问题? Webpack 是实现前端项目的模块化,用于现代 JavaScript 应用程序的静态模块打包工具,被webpack 直接引用的资源打包进 bunde.js的资源,当webpack 处理应用程序时,它会在内部构建一…...

【机器学习之旅】概念启程、步骤前行、分类掌握与实践落地
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...
外星人m18R2国行中文版原厂预装23H2原装Win11系统恢复带F12恢复重置
戴尔外星人m18R2国行中文版原厂预装23H2系统恢复安装 远程恢复安装:https://pan.baidu.com/s/166gtt2okmMmuPUL1Fo3Gpg?pwdm64f 提取码:m64f 1.自带原厂预装系统各驱动,主题,Logo,Office带所有Alienware主题壁纸、Alienware软件驱动 2.带…...
libVLC 视频抓图
Windows操作系统提供了多种便捷的截图方式,常见的有以下几种: 全屏截图:通过按下PrtSc键(Print Screen),可以截取整个屏幕的内容。截取的图像会保存在剪贴板中,可以通过CtrlV粘贴到图片编辑工具…...

Docker搭建LNMP环境实战(06):Docker及Docker-compose常用命令
Docker搭建LNMP环境实战(06):Docker及Docker-compose常用命令 此处列举了docker及docker-compose的常用命令,一方面可以做个了解,另一方面可以在需要的时候进行查阅。不一定要强行记忆,用多了就熟悉了。 1、…...

ClickHouse10-ClickHouse中Kafka表引擎
Kafka表引擎也是一种常见的表引擎,在很多大数据量的场景下,会从源通过Kafka将数据输送到ClickHouse,Kafka作为输送的方式,ClickHouse作为存储引擎与查询引擎,大数据量的数据可以得到快速的、高压缩的存储。 Kafka大家…...

Encoding类
Encoding System.Text.Encoding 是 C# 中用于处理字符编码和字符串与字节之间转换的类。它提供了各种静态方法和属性,**用于在不同字符编码之间进行转换,**以及将字符串转换为字节数组或反之。 在处理多语言文本、文件、网络通信以及其他字符数据的场景…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
