刚刚,百度和苹果宣布联名
百度 × Apple
就在刚刚,财联社报道,百度将为苹果今年发布的 iPhone16、Mac 系统和 iOS18 提供 AI 功能。
苹果曾与阿里以及另外一家国产大模型公司进行过洽谈,最后确定由百度提供这项服务,苹果预计采取 API 接口的方式计费。
苹果将国行 iPhone 等设备采用国产大模型 AI 功能主要出于合规需求,因为苹果自身短期内还无法解决合规问题,但国外版 iPhone 等设备 AI 功能均来自苹果自己的大模型。
不是黑百度(我们要正视客观差距),相信大多数国行用户心理多少有点不是滋味,国产苹果味 🤣
为什么说大多数,而不是所有国行用户,剩下的小部分是什么人。
是持有「百度」股票的国行用户:
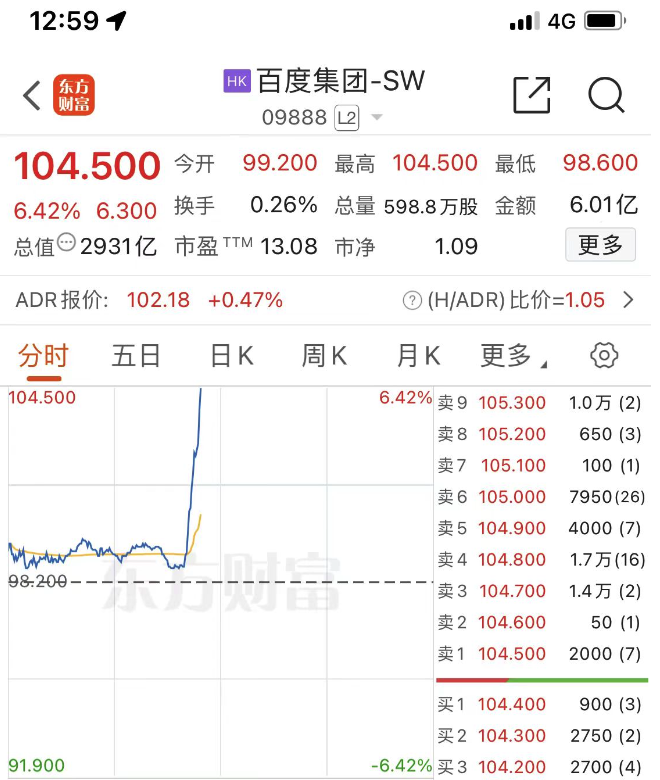
蹭上了果链,百度盘中上涨 6 个点。
本文发出的时候,H 股那边还没收盘,但基本可以断定结局。
中国公司,不管你是 A 股、H 股还是美股,都自带「出利好 = 高开低走」的传统艺能。
关于「百度」和「Apple」本次联名,你怎么看?是否会考虑放弃保修买入海外版?
...
回归主线。
来做一道和「百度」社招相关的算法面试题。
题目描述
平台:LeetCode
题号:649
Dota2 的世界里有两个阵营:Radiant(天辉)和 Dire(夜魇)。
Dota2 参议院由来自两派的参议员组成,现在参议院希望对一个 Dota2 游戏里的改变作出决定,他们以一个基于轮为过程的投票进行。
在每一轮中,每一位参议员都可以行使两项权利中的一项:
-
禁止一名参议员的权利:参议员可以让另一位参议员在这一轮和随后的几轮中丧失所有的权利 。 -
宣布胜利:如果参议员发现有权利投票的参议员都是同一个阵营的,他可以宣布胜利并决定在游戏中的有关变化。
给你一个字符串 s 代表每个参议员的阵营。字母 'R' 和 'D'分别代表了 Radiant(天辉)和 Dire(夜魇)。
然后,如果有 n 个参议员,给定字符串的大小将是 n。
以轮为基础的过程从给定顺序的第一个参议员开始到最后一个参议员结束,这一过程将持续到投票结束,所有失去权利的参议员将在过程中被跳过。
假设每一位参议员都足够聪明,会为自己的政党做出最好的策略,你需要预测哪一方最终会宣布胜利并在 Dota2 游戏中决定改变。
输出应该是 "Radiant" 或 "Dire"。
示例 1:
输入:s = "RD"
输出:"Radiant"
解释:
第 1 轮时,第一个参议员来自 Radiant 阵营,他可以使用第一项权利让第二个参议员失去所有权利。
这一轮中,第二个参议员将会被跳过,因为他的权利被禁止了。
第 2 轮时,第一个参议员可以宣布胜利,因为他是唯一一个有投票权的人。
示例 2:
输入:s = "RDD"
输出:"Dire"
解释:
第 1 轮时,第一个来自 Radiant 阵营的参议员可以使用第一项权利禁止第二个参议员的权利。
这一轮中,第二个来自 Dire 阵营的参议员会将被跳过,因为他的权利被禁止了。
这一轮中,第三个来自 Dire 阵营的参议员可以使用他的第一项权利禁止第一个参议员的权利。
因此在第二轮只剩下第三个参议员拥有投票的权利,于是他可以宣布胜利
提示:
-
-
-
senate[i]为'R'或'D'
基本分析
整理题意:每次选择对方的一个成员进行消除,直到所有剩余成员均为我方时,宣布胜利。
由于每个对方成员执行权利都意味着我方损失一名成员,因此最佳方式是 「尽量让对方的权利不执行,或延迟执行(意味着我方有更多执行权利的机会)」。因此,最优决策为 「每次都选择对方的下一个行权成员进行消除」。
贪心
这个找“最近一个”对方行权成员的操作既可以使用「有序集合」来做,也可以使用「循环队列」来做。
先说使用「有序集合」的做法。
起始我们先将 s 中的 Radiant 和 Dire 分别存入有序集合 rs 和 ds 当中,然后从前往后模拟消除过程,过程中使用 idx 代表当前处理到的成员下标,使用 set 记录当前哪些成员已被消除。
当轮到 s[idx] 行权时(若 s[idx] 已被消除,则跳过本轮),从对方的有序队列中取出 「首个大于等于 idx 的下标」(取出代表移除);若对方的有序序列不存在该下标,而行权过程又是循环进行的,说明此时下一个行权的对方成员是 「首个大于等于 」 的下标,我们对其进行取出消除,随后往后继续决策。
Java 代码:
class Solution {
public String predictPartyVictory(String s) {
TreeSet<Integer> rs = new TreeSet<>(), ds = new TreeSet<>();
int n = s.length();
for (int i = 0; i < n; i++) {
if (s.charAt(i) == 'R') rs.add(i);
else ds.add(i);
}
Set<Integer> set = new HashSet<>();
int idx = 0;
while (rs.size() != 0 && ds.size() != 0) {
if (!set.contains(idx)) {
TreeSet<Integer> temp = null;
if (s.charAt(idx) == 'R') temp = ds;
else temp = rs;
Integer t = temp.ceiling(idx);
if (t == null) t = temp.ceiling(0);
set.add(t);
temp.remove(t);
}
idx = (idx + 1) % n;
}
return rs.size() != 0 ? "Radiant" : "Dire";
}
}
不难发现,虽然将所有成员存入有序集合和取出的复杂度均为 ,但整体复杂度仍是大于 。
因为我们在每一轮的消除中,从 idx 位置找到下一个决策者,总是需要遍历那些已被消除的位置,而该无效遍历操作可使用「循环队列」优化。
优化
使用循环队列 rd 和 dd 来取代有序集合 rs 和 ds。起始将各个成员分类依次入队,每次从两队列队头中取出成员,假设从 rs 中取出成员下标为 a,从 dd 中取出成员下标为 b,对两者进行比较:
-
若有 a < b,说明a先行权,且其消除对象为b,a行权后需等到下一轮,对其进行大小为 的偏移后重新添加到rd尾部(含义为本次行权后需要等到下一轮); -
若有 b < a,同理,将a消除后,对b进行大小为 的偏移后重新添加到dd尾部。
Java 代码:
class Solution {
public String predictPartyVictory(String s) {
Deque<Integer> rd = new ArrayDeque<>(), dd = new ArrayDeque<>();
int n = s.length();
for (int i = 0; i < n; i++) {
if (s.charAt(i) == 'R') rd.addLast(i);
else dd.addLast(i);
}
while (rd.size() != 0 && dd.size() != 0) {
int a = rd.pollFirst(), b = dd.pollFirst();
if (a < b) rd.addLast(a + n);
else dd.addLast(b + n);
}
return rd.size() != 0 ? "Radiant" : "Dire";
}
}
C++ 代码:
class Solution {
public:
string predictPartyVictory(string s) {
deque<int> rd, dd;
int n = s.length();
for (int i = 0; i < n; i++) {
if (s[i] == 'R') rd.push_back(i);
else dd.push_back(i);
}
while (!rd.empty() && !dd.empty()) {
int a = rd.front(), b = dd.front();
rd.pop_front();
dd.pop_front();
if (a < b) rd.push_back(a + n);
else dd.push_back(b + n);
}
return !rd.empty() ? "Radiant" : "Dire";
}
};
Python 代码:
from collections import deque
class Solution:
def predictPartyVictory(self, s: str) -> str:
rd, dd = deque(), deque()
n = len(s)
for i in range(n):
if s[i] == 'R':
rd.append(i)
else:
dd.append(i)
while rd and dd:
a, b = rd.popleft(), dd.popleft()
if a < b:
rd.append(a + n)
else:
dd.append(b + n)
return "Radiant" if rd else "Dire"
TypeScript 代码:
function predictPartyVictory(s: string): string {
let rd: Array<number> = [], dd: Array<number> = [];
let n: number = s.length;
for (let i = 0; i < n; i++) {
if (s.charAt(i) == 'R') rd.push(i);
else dd.push(i);
}
while (rd.length != 0 && dd.length != 0) {
let a: number = rd.shift()!, b: number = dd.shift()!;
if (a < b) rd.push(a + n);
else dd.push(b + n);
}
return rd.length != 0 ? "Radiant" : "Dire";
};
-
时间复杂度:将所有成员进行分队,复杂度为 ;每个回合会有一名成员被消除,最多有 个成员,复杂度为 。整体复杂度为 -
空间复杂度:
最后
给大伙通知一下 📢 :
全网最低价 LeetCode 会员目前仍可用!!!
📅 年度会员:有效期加赠两个月!!; 季度会员:有效期加赠两周!!
🧧 年度会员:获 66.66 现金红包!!; 季度会员:获 22.22 现金红包!!
🎁 年度会员:参与当月丰厚专属实物抽奖(中奖率 > 30%)!!
专属链接:https://leetcode.cn/premium/?promoChannel=acoier
更多详情请戳 这里 。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
相关文章:

刚刚,百度和苹果宣布联名
百度 Apple 就在刚刚,财联社报道,百度将为苹果今年发布的 iPhone16、Mac 系统和 iOS18 提供 AI 功能。 苹果曾与阿里以及另外一家国产大模型公司进行过洽谈,最后确定由百度提供这项服务,苹果预计采取 API 接口的方式计费。 苹果将…...

HTTP系列之HTTP缓存 —— 强缓存和协商缓存
文章目录 HTTP缓存强缓存协商缓存状态码区别缓存优先级如何设置强缓存和协商缓存使用场景 HTTP缓存 HTTP缓存时利用HTTP响应头将所请求的资源在浏览器进行缓存,缓存方式分两种:强缓存和协商缓存。 浏览器缓存是指将之前请求过的资源在浏览器进行缓存&am…...
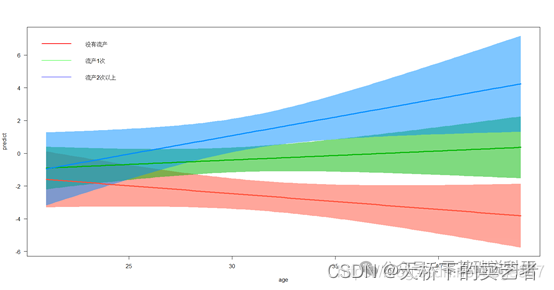
代码+视频,R语言logistic回归交互项(交互作用)的可视化分析
交互作用效应(p for Interaction)在SCI文章中可以算是一个必杀技,几乎在高分的SCI中必出现,因为把人群分为亚组后再进行统计可以增强文章结果的可靠性,不仅如此,交互作用还可以使用来进行数据挖掘。在既往文章中,我们已…...

实验3 中文分词
必做题: 数据准备:academy_titles.txt为“考硕考博”板块的帖子标题,job_titles.txt为“招聘信息”板块的帖子标题,使用jieba工具对academy_titles.txt进行分词,接着去除停用词,然后统计词频,最…...
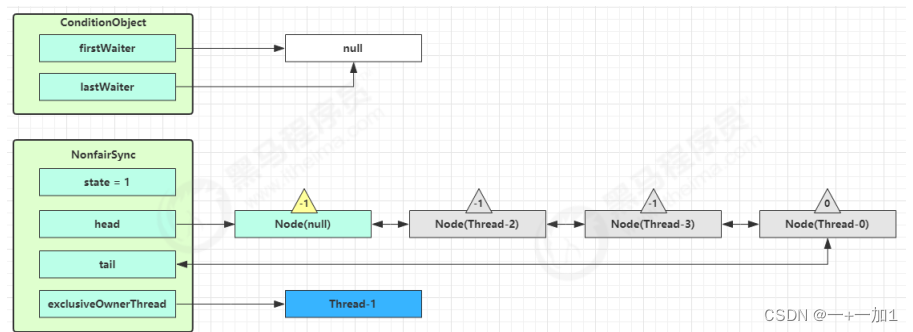
ReentrantLock 原理
(一)、非公平锁实现原理 1、加锁解锁流程 先从构造器开始看,默认为非公平锁实现 public ReentrantLock() {sync new NonfairSync(); } NonfairSync 继承自 AQS 没有竞争时 加锁流程 构造器构造,默认构造非公平锁(无竞争,第一个线程尝试…...
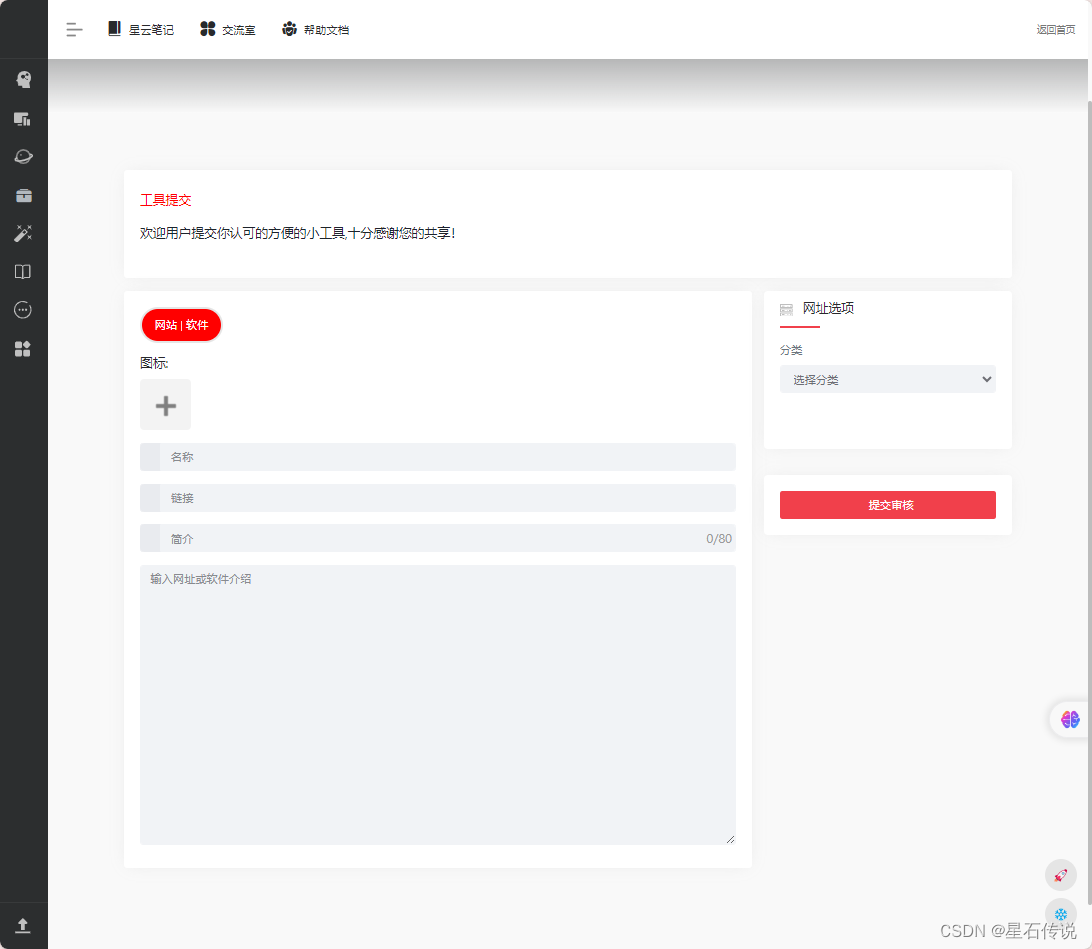
星云小窝项目1.0——项目介绍(一)
星云小窝项目1.0——项目介绍(一) 文章目录 前言1. 介绍页面2. 首页2.1. 游客模式2.2. 注册用户后 3. 星云笔记3.1. 星云笔记首页3.2. 星云笔记 个人中心3.2. 星云笔记 系统管理3.3. 星云笔记 文章展示3.3. 星云笔记 新建文章 4. 数据中心5. 交流评论6. …...

VR虚拟仿真在线模拟旅游专业情景
旅游专业运用VR虚拟仿真教学的教学优势主要包括: 1. 增强教学效果:VR技术能够提供身临其境的体验,使学生更容易理解和记住某些概念和理论。例如,学生可以通过虚拟旅行来了解某个国家的文化、历史和景点,这将比传统的课…...
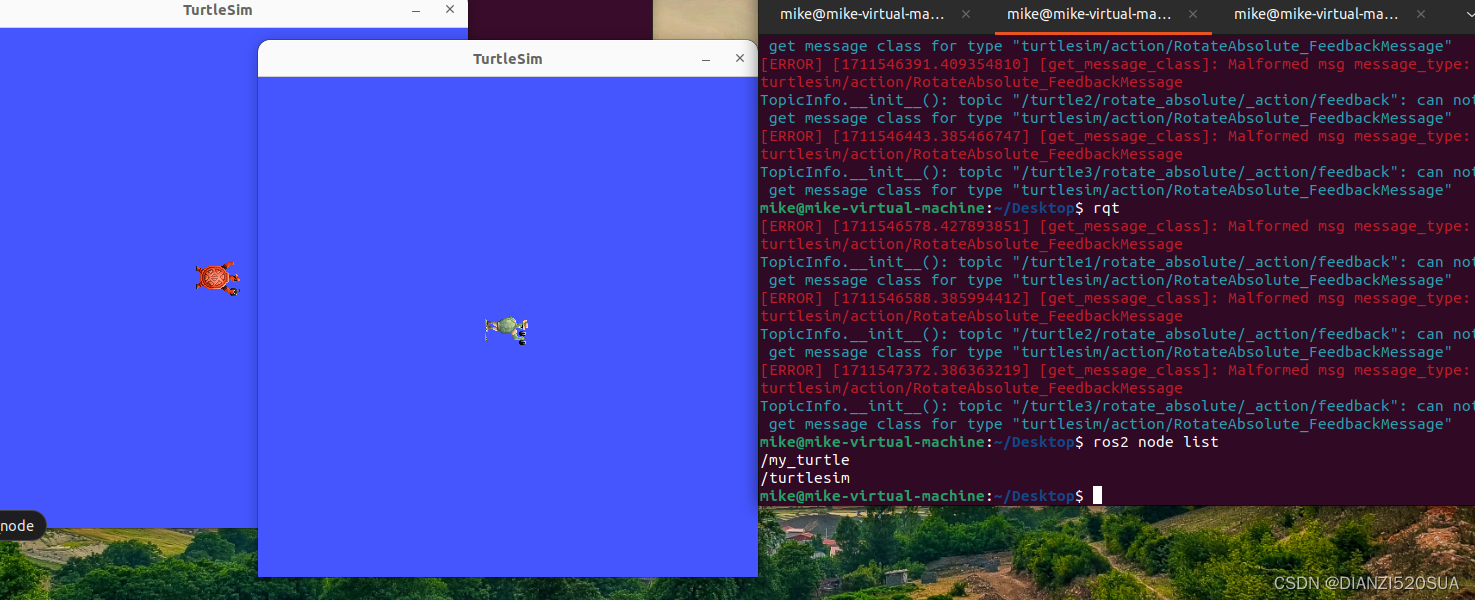
ROS 2边学边练(3)-- 何为节点(nodes)
在接触节点这个概念之前,我们先来看看下面这张动态图,更方便我们理解一些概念和交互过程。 (相信大家的英文基础哈) 概念 如上图所示,这里面其实涉及到了三个概念(功能),分别是节点…...

MySQL的主从复制和读写分离
目录 相关知识: 1. 主从复制和读写分离 2. mysql 支持的复制类型 对比: 一. 主从复制 1. 原理和工作过程 工作过程: 注意: 中继日志(Relay Log): 2. 一些理解问题 2.1 为什么要复制 …...

C# 多态 派生类 abstract virtual new
静态多态函数重载运算符重载 动态多态abstract 和 virtual的区别定义与用途:成员实现:继承与重写:与接口的区别: 使用抽象类的好处主要体现在以下几个方面:代码重用:设计灵活性:接口定义&#x…...
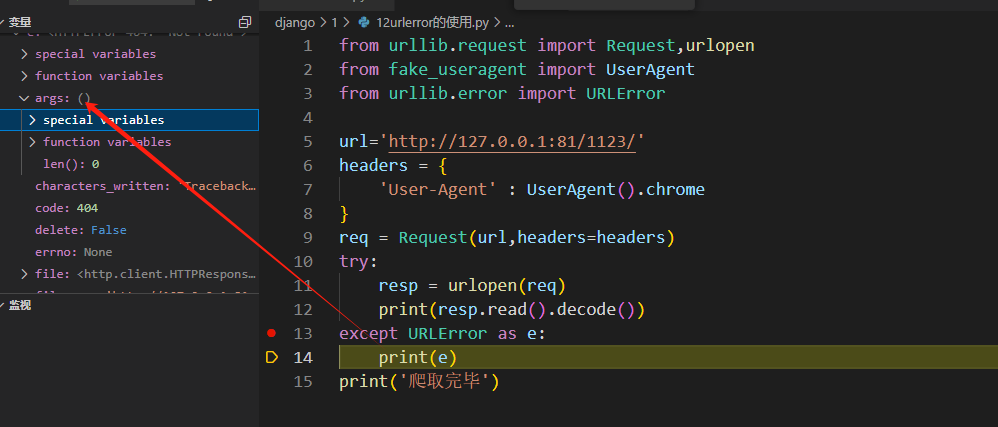
【爬虫基础】第10讲 urlerror的使用及捕获异常
URLError是Python中的一个异常类,用于处理与URL相关的错误。它是urllib.error模块中的一个类。 URLError通常在以下情况下被引发: 网络连接问题:例如无法连接到服务器、超时等。URL不正确:例如无效的URL、无法解析主机名等。服务…...

绍兴越城中墙建材蒸压加气混凝土砌块使用注意事项可送塔山府山北海蕺山城南稽山迪荡灵芝东湖皋埠马山斗门鉴湖东浦孙端陶堰富盛
绍兴越城中墙建材蒸压加气混凝土砌块使用注意事项可送塔山府山北海蕺山城南稽山迪荡灵芝东湖皋埠马山斗门鉴湖东浦孙端陶堰富盛 使用蒸压加气混凝土砌块时需要注意以下事项: 选择符合国家标准的产品:选购时应查看产品质量证明书,确保产品符合…...

吴渔夫:AI技术引领游戏产业革命,小团队有大作为
AI技术的突飞猛进,游戏产业正在经历一场前所未有的变革。中国网游先锋,火石控股创始人吴渔夫,近日在接受第一财经日报的采访,对AI在游戏制作中的应用和未来趋势有着深刻的见解。 吴渔夫指出,AI技术的引入极大地降低了游…...
)
深入探索C++对象模型(二)
类对象占用的空间 #include "pch.h" #include <iostream> using namespace std;class A {public: };//类对象所占用的空间 int main() {//std::cout << "Hello World!\n"; A obja;int ilen = sizeof(obja); cout << ilen << endl…...

【javaWeb 第三篇】Vue快速入门
VUE vue是一套前端框架,免除原生的js的DOM操作,简化书写 基于MVVM(model-view-viewmodel)思想,实现数据的双向绑定,将编程的关注放在数据上。 什么是框架: 框架相当于一个半成品,是一…...
命令记录)
非root用户安装git lfs(git大文件)命令记录
背景 最近在看LLAMA2的模型,想直接从Huggingface下载模型到本地,但是却发现服务器上没有安装git lfs命令。查询了一些资料完成了非root用户安装git lfs命令的操作,特此记录。 Git LFS下载与解压 下载 Git LFS 二进制文件 访问 Git LFS 发布…...

PTA 道路管制
乌拉乌拉国有n个城市和m条道路,城市编号为1∼n。由于乌拉乌拉国每一个城市都在创城(创建文明城市),因此,城市之间的道路通行施行道路交通管制: 已知从城市ui到城市vi的道路,需要时间ti。…...
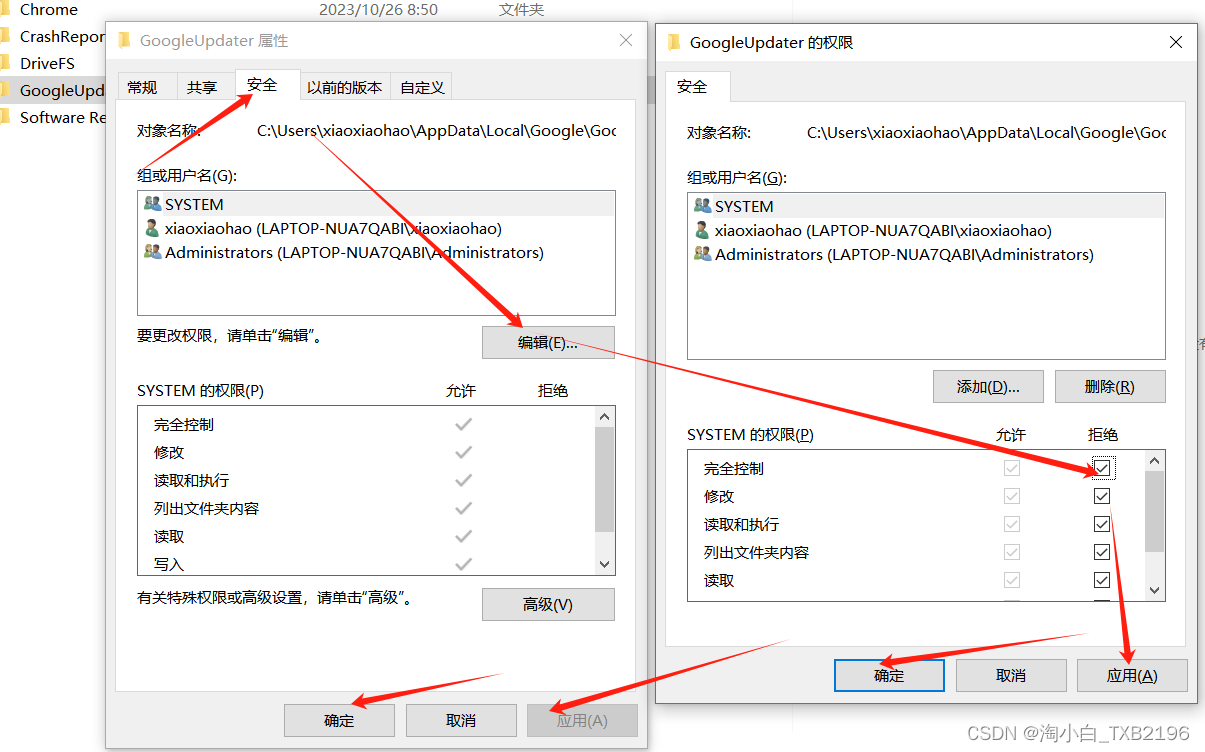
自媒体用ChatGPT批量洗稿软件V5.9环境配置/软件设置教程【汇总】
大家好,我是淘小白~ 首先,感谢大家的支持~~ ChatGPT采集洗稿软件V5.9版本更新,此次版本更新修改增加了一些内容: 1、自定义多条指令,软件自动判断指令条数,进行输入 2、增加谷歌浏览多账号轮询…...

【WPF应用7】 基本控件-Grid 布局的详解与示例
引言 WPF(Windows Presentation Foundation)是.NET框架的一部分,它提供了一个用于创建桌面应用程序用户界面的框架。在WPF中,Grid布局是一个非常强大的布局工具,它允许开发者创建复杂的、响应迅速的用户界面布局。Grid…...

flink-connector-redis支持select查询
EN 1 项目介绍 基于bahir-flink二次开发,相对bahir调整的内容有: 1.使用Lettuce替换Jedis,同步读写改为异步读写,大幅度提升了性能 2.增加了Table/SQL API,增加select/维表join查询支持 3.增加关联查询缓存(支持增量与全量) 4…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
