【滑动窗口】Leetcode 串联所有单词的子串
题目解析
30. 串联所有单词的子串

本题的意思就是在目标串s中寻找能够找到的words字符串的全排列,返回起始位置
算法讲解

我们可以将这道题转化为寻找目标串的words字母的异位词,按照上一次讲解的【滑动窗口】Leetcode 找到字符串中所有字母异位词我们还是使用同样的做法,哈希表 + 滑动窗口
但是这道题有以下注意事项:滑动窗口的移动次数
每一次left和right一开始都指向同一个位置,当滑动窗口移动到字符串s结束的时候,需要将left+1,开始继续滑动下一次的循环
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {unordered_map<string, int> Hash_words;vector<int>ret;int left = 0;int right = 0;//将words放进Hashfor (auto str : words){Hash_words[str]++;}int count = 0;int cnt = 0;//窗口一次移动完成之后再从一开始的下一个位置反复while (cnt < words[0].size()){//这是一次完整的移动unordered_map<string, int> hash2; // 维护窗⼝内单词的频次for (int left = cnt, right = cnt, count = 0; right + words[0].size() <= s.size(); right += words[0].size()){// 进窗⼝ + 维护 countstring temp = s.substr(right, words[0].size());hash2[temp]++;//这里hash2[temp] == Hash_words[temp]时,还需要再count++,因为有可能遇到s中连续相同的串,我要确保当前位置的串和后面的串能利用上if (Hash_words.count(temp) && hash2[temp] <= Hash_words[temp]){count++;}// 判断if (right - left + 1 > (words.size() * words[0].size())){// 出窗⼝ + 维护 countstring out = s.substr(left, words[0].size());if (Hash_words.count(out) && hash2[out] <= Hash_words[out]) count--;hash2[out]--;left += words[0].size();}// 更新结果if (count == words.size()){ret.push_back(left);}}cnt++;}return ret;
}
};
相关文章:

【滑动窗口】Leetcode 串联所有单词的子串
题目解析 30. 串联所有单词的子串 本题的意思就是在目标串s中寻找能够找到的words字符串的全排列,返回起始位置 算法讲解 我们可以将这道题转化为寻找目标串的words字母的异位词,按照上一次讲解的【滑动窗口】Leetcode 找到字符串中所有字母异位词我们…...

golang channel实践代码及注意事项
在使用Go语言(Golang)的通道(Channel)时,有几个重要的注意点可以帮助开发者更安全、高效地使用它们进行并发编程。以下是一些关键的注意事项: 选择正确的通道类型:Go语言提供了两种类型的通道&…...

面试题:RabbitMQ 消息队列中间件
1. 确保消息不丢失 生产者确认机制 确保生产者的消息能到达队列,如果报错可以先记录到日志中,再去修复数据持久化功能 确保消息未消费前在队列中不会丢失,其中的交换机、队列、和消息都要做持久化消费者确认机制 由spring确认消息处理成功后…...

wpf中引用自定义字体
在WPF(Windows Presentation Foundation)中,FontFamily属性用于指定控件或文本元素使用的字体。它是一个非常基础且重要的属性,影响着用户界面的视觉呈现和可读性。以下是关于WPF中FontFamily属性的一些关键信息和使用方法&#x…...

高效准确!指甲剪盖片视觉检测技术解密
指甲剪的盖片是指指甲剪的一端,通常用来盖住另一端的刀刃部分。指甲剪盖片是指甲剪的重要部分,除了保护刀刃外,还起到美观和便捷的作用。正确使用和保养指甲剪盖片可以延长指甲剪的使用寿命。 本案是对指甲剪盖片最大尺寸长75mm*宽10mm*高3mm…...

分布式IO模块PLC扩展模拟量模块
BL200是一款结构紧凑、体积小的分布式IO耦合器,支持ModbusTCP协议,采用嵌入式硬件,主频380Mhz,基于LinuxOS,采用独特的MAC层数据交换技术的双网口技术实现级联,中间设备宕机不影响后面设备的数据传输,可支持高达32个AI、DI、DO、热电阻、热电偶、RS485等种类的IO板,广泛应用于工…...

Qt事件系统
第三章Qt事件系统 文章目录 第三章Qt事件系统1.事件系统事件是如何传递的事件类型事件处理发送事件 2.事件传播机制事件接受和忽略事件分发事件过滤 3.事件和信号的区别 1.事件系统 在Qt中,事件是派生抽象QEvent类的对象,它表示应用程序内发生的事情&am…...

C++STL--排序算法
sort 使用快速排序,平均性能好O(nlogn),但最差情况可能很差O(n^2)。不稳定。 sort(v.begin(),v.end());//对v容器进行排序,默认升序 sort(v.begin(),v.end(),greater<int>());//降序排序对于支持随机访问的迭代器的容器, 都可以利用sort算法直接对其进行排序…...

CEF的了解
(14 封私信 / 80 条消息) CEF和Electron的区别是什么? - 知乎 (zhihu.com) Electron面向的开发者:会用JavaScript,HTML,CSS,不会C CEF面向的开发者:会用JavaScript,HTML,CSS,会C (14 封私信 / 80 条消息) liulun - …...

基于OrangePi Zero2的智能家居项目(开发阶段)
智能家居项目的软件实现 紧接上文 基于OrangePi Zero2的智能家居项目(准备阶段)-CSDN博客 目录 一、项目整体设计 1.1项目整体设计 1.2具体划分 二、开发工作的前期准备 1、进行分类,并用Makefile文件进行管理 参考:自己创…...

数据结构记录
之前记录的数据结构笔记,不过图片显示不了了 数据结构与算法(C版) 1、绪论 1.1、数据结构的研究内容 一般应用步骤:分析问题,提取操作对象,分析操作对象之间的关系,建立数学模型。 1.2、基本概念和术语 数据&…...
从零到一:基于 K3s 快速搭建本地化 kubeflow AI 机器学习平台
背景 Kubeflow 是一种开源的 Kubernetes 原生框架,可用于开发、管理和运行机器学习工作负载,支持诸如 PyTorch、TensorFlow 等众多优秀的机器学习框架,本文介绍如何在 Mac 上搭建本地化的 kubeflow 机器学习平台。 注意:本文以 …...

kettle使用MD5加密增量获取接口数据
kettle使用MD5加密增量获取接口数据 场景介绍: 使用JavaScript组件进行MD5加密得到Http header,调用API接口增量获取接口数据,使用json input组件解析数据入库 案例适用范围: MD5加密可参考、增量过程可参考、调用API接口获取…...
PS入门|黑白色的图标怎么抠成透明背景
前言 抠图可以算是PS的入门必备操作,开始学习PS的小伙伴可以根据本帖子推荐一步步学习哦!但切勿心急~ 今天给小伙伴们带来:黑白色的图标抠图教程 抠图有很多种方法,但根据类型的不同,使用适当的方法很重…...
apexd 启动)
android 14 apexd分析(2)apexd 启动
1. class main进程一起启动, apexservice是他提供的binderservice,这也第二阶段的最主要的作用 /system/apex/apexd/apexd.rc?r3c8e8603c640fc41e0406ddcf981381803447cfb#1 1 service apexd /system/bin/apexd 2 interface aidl apexservice …...

微信小程序怎么制作?制作一个微信小程序需要多少钱?
随着移动互联网的快速发展,微信小程序已成为连接用户与服务的重要桥梁。它以其便捷性和易用性,为各类企业和个人提供了一个全新的展示和交易平台。那么,如何制作一个微信小程序?又需要投入多少资金呢?本文将为您提供全…...
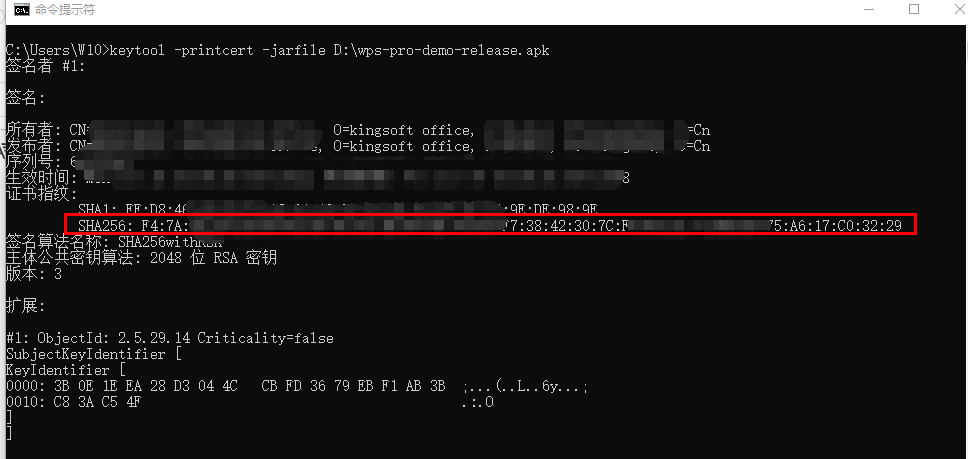
WPS二次开发专题:如何获取应用签名SHA256值
作者持续关注WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 在申请WPS SDK授权版时候需要开发者提供应用包名和签…...

Flink SQL系列之:基于Flink SQL查询Topic中序列化的Debezium数据格式字段
Flink SQL系列之:基于Flink SQL查询Topic中序列化的Debezium数据格式字段 一、表结构二、查询Topic中表的数据三、反序列化字段一、表结构 CREATE TABLE IF NOT EXISTS record_rt (id decimal(20,0) COMMENT "主键",follow_entity_type <...

【WPF应用30】WPF中的ListBox控件详解
WPF(Windows Presentation Foundation)是.NET框架的一个组成部分,用于构建桌面应用程序的用户界面。ListBox是WPF中一个非常常用的控件,用于显示一系列的项,用户可以选择单个或多个项。 1.ListBox的基本概念 ListBox…...

Chatgpt掘金之旅—有爱AI商业实战篇(二)
演示站点: https://ai.uaai.cn 对话模块 官方论坛: www.jingyuai.com 京娱AI 一、前言: 成为一名商业作者是一个蕴含着无限可能的职业选择。在当下数字化的时代,作家们有着众多的平台可以展示和推广自己的作品。无论您是对写书、文…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...
