CF756div3 vp
又被薄纱了,rk就不放了,好丢人QwQ
Dashboard - Codeforces Round 756 (Div. 3) - Codeforces
A. Make Even
小分类讨论
题意:
给定一个数,每次操作可以选取其前缀然后翻转其前缀,问你最少操作几次可以把该数变为偶数
思路:
对次数分类讨论即可
如果本来就是偶数,就是0次
如果s[1]是偶数,翻转一整个就行
如果没有偶数位,就是-1
其余都是两次
Code:
#include <bits/stdc++.h>
//#define int long long
#define LL long long
const int mxn=1e6+10;
const int mxe=2e5+10;
const int mod=1e9+7;
using namespace std;string s;
void solve(){s.clear();cin>>s;int n=s.size();s=" "+s;if((s[n]-'0')%2==0) cout<<0<<'\n';else if((s[1]-'0')%2==0) cout<<1<<'\n';else{int ok=0;for(int i=1;i<=n;i++){if((s[i]-'0')%2==0) ok=1;}if(ok) cout<<2<<'\n';else cout<<-1<<'\n';}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;cin>>__;//p_init(1e6);while(__--)solve();return 0;
}B. Team Composition: Programmers and Mathematicians
贪心
题意:
有a个数学家和b个计算机学家,4个人一组组队,每组至少包含两种学科,问最多能组几队
谢谢,不会小学数学
思路:
要使队伍数尽可能多,就让少的那个学科每队派一人,然后和另一个队组队
那么答案就是min(min(a,b),(a+b)/4)
Code:
#include <bits/stdc++.h>
//#define int long long
#define LL long long
const int mxn=1e6+10;
const int mxe=2e5+10;
const int mod=1e9+7;
using namespace std;int a,b;
void solve(){cin>>a>>b;cout<<min(min(a,b),(a+b)/4)<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;cin>>__;//p_init(1e6);while(__--)solve();return 0;
}C. Polycarp Recovers the Permutation
构造+排列
题意:

思路:
一开始写了一小时的双指针模拟操作,然后写了一坨错了
这是构造题,考虑将一些一般条件特殊化,一般来说这种一般条件都是比较难处理的,像之前过年那会有个子序列,它就直接选了一整个序列,对于这种难处理的一般条件,我们考虑将其特殊化
注意到答案的排列(即原来的排列)的两端一定是最大值,否则就是无解
这道题就是把 双指针每次选小的那个 这个条件 转化成 固定一个指针动另一个,固定的那个指针大小一定为n,直接将其翻转即可
Code:
#include <bits/stdc++.h>
using namespace std;
//#pragma GCC optimize(2)
#define close(); ios::sync_with_stdio(false);
#define endl '\n'
#define rep(i, l, r) for(int i = l; i <= r; i++)
#define dwn(i, r, l) for(int i = r; i >= l; i--)
typedef long long LL;
const int N = 3e5+100;
int a[N];
int b[N];
void solve()
{int n; cin >> n;rep(i, 1, n) cin >> a[i];if(a[1] == n || a[n] == n){dwn(i, n, 1) cout << a[i] << " "; cout << endl;}else cout << -1 << endl;}int main()
{close();int T; cin >> T;while(T--) solve();// system("pause");
}F. ATM and Students
尺取法
题意:
找出最长的连续子串使得其前缀和+s>=0
思路:
尺取法模板题,这道题居然有*1800,逆
Code:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mxn=2e5+10;int n,s;
int a[mxn],sum[mxn];
void solve(){memset(sum,0,sizeof(sum));cin>>n>>s;for(int i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i];int ans=-1,ansl,ansr;for(int l=1,r=1;l<=n;l++){while(r<=n&&sum[r]-sum[l-1]>=-s) r++;r--;if(ans<r-l+1){ans=r-l+1;ansl=l;ansr=r;}}if(ans==-1||ansl>ansr) cout<<-1<<'\n';else cout<<ansl<<" "<<ansr<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;cin>>__;while(__--)solve();return 0;
}D. Weights Assignment For Tree Edges
构造
题意:
给定一棵树
又给了一个排列,对于p[i]满足dis[p[i]]>dis[p[i-1]]
dis是该结点的树上前缀和,w是边权
要你给这棵树的边权w赋值,使得能满足p排列的条件

思路:
模拟一下样例发现,我们可以遍历p[i]排列,把边权变成公差为1 的等差数列(特殊化边权)
如果父亲结点在p[i]中出现的id大于结点i,那么父亲结点的dis必然小于结点i,矛盾,所以这种情况无解
否则就去递推出p[i]的dis和w
Code:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mxn=2e5+10;int n,rt;
int fa[mxn],w[mxn],dis[mxn],id[mxn],p[mxn];
void solve(){memset(dis,0,sizeof(dis));memset(w,0,sizeof(w));cin>>n;for(int i=1;i<=n;i++){cin>>fa[i];if(fa[i]==i) rt=i;}for(int i=1;i<=n;i++){cin>>p[i];id[p[i]]=i;}if(p[1]!=rt) cout<<-1<<'\n';else{int ok=1;for(int i=2;i<=n;i++){if(id[p[i]]<id[fa[p[i]]]) ok=0;w[p[i]]=dis[p[i-1]]+1-dis[fa[p[i]]];dis[p[i]]=dis[fa[p[i]]]+w[p[i]];}if(!ok) cout<<-1<<'\n';else{for(int i=1;i<=n;i++) cout<<w[i]<<" \n"[i==n];}}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;cin>>__;while(__--)solve();return 0;
}E1. Escape The Maze (easy version)
BFS
题意:
有一棵树,Vlad和n个朋友玩游戏,Vlad位于节点1,n个朋友位于其他节点,第i个朋友位于xi。每个时刻,每个人都能沿着树边到达另一个点,或者留在原地。如果Vlad到达叶子节点,则Vlad赢。如果在其到达叶子前和其他人碰面(叶子也不能有其他人),则Vlad输。问最少需要保留多少个人能够保证Vlad输,即选取朋友的一个最小的子集,使得Vlad不能赢。
思路:
直接去BFS模拟过程,一格格染色,如果能把叶子结点染成1就是赢
Code:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mxn=2e5+10;
const int mxe=2e5+10;
struct ty{int to,next;
}edge[mxe<<1];
queue<int> q;int n,k,u,v;
int tot=0,ok=0;
int x[mxn],d[mxn],head[mxn],mark[mxn],vis[mxn];
void add(int u,int v){edge[tot].to=v;edge[tot].next=head[u];head[u]=tot++;
}
void init(){tot=0;ok=0;for(int i=0;i<=n;i++){x[i]=0;head[i]=-1;d[i]=0;mark[i]=0;vis[i]=0;}
}
bool bfs(){for(int i=1;i<=k;i++) q.push(x[i]),vis[x[i]]=1;q.push(1);vis[1]=1;mark[1]=1;while(!q.empty()){int u=q.front();q.pop();if(d[u]==1&&mark[u]==1&&u!=1) ok=1;for(int i=head[u];~i;i=edge[i].next){if(vis[edge[i].to]) continue;vis[edge[i].to]=1;q.push(edge[i].to);mark[edge[i].to]=mark[u];}}return ok;
}
void solve(){cin>>n>>k;init();for(int i=1;i<=k;i++) cin>>x[i];for(int i=1;i<=n-1;i++){cin>>u>>v;add(u,v);add(v,u);d[v]++;d[u]++;}//for(int i=1;i<=n;i++) if(d[i]==1) cout<<i<<'\n';if(bfs()) cout<<"YES"<<'\n';else cout<<"NO"<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;cin>>__;while(__--)solve();return 0;
}相关文章:

CF756div3 vp
又被薄纱了,rk就不放了,好丢人QwQDashboard - Codeforces Round 756 (Div. 3) - CodeforcesA. Make Even小分类讨论题意:给定一个数,每次操作可以选取其前缀然后翻转其前缀,问你最少操作几次可以把该数变为偶数思路&am…...
Linux命令·less
less 工具也是对文件或其它输出进行分页显示的工具,应该说是linux正统查看文件内容的工具,功能极其强大。less 的用法比起 more 更加的有弹性。在 more 的时候,我们并没有办法向前面翻, 只能往后面看,但若使用了 less …...

修改redis改key值不改过期时间
今天在做图片验证码的时候遇到一个问题。用redis的生命周期来存放,用户输入错误次数。 三十秒内输错三次就,等待三十分钟。 那么问题来了,如果说第一次输入错误,应该是 key为用户用,value 为 次数2 ex就为30秒 &…...

Spark的DataFrame使用
内容目录创建SparkSession对象从CSV文件中读取从JSON文件中读取从Parquet文件中读取从数据列表中创建DataFrame从字典列表中创建DataFrame选择一列选择多列过滤年龄大于30的数据过滤名字为Alice的数据可以使用and、or、not等操作符进行组合查询按照年龄分组并计算平均年龄和最大…...

【Flutter】入门Dart语言:操作符的基本用法
文章目录 一、前言二、常用的操作符1.算术操作符2.关系操作符3.逻辑操作符4.赋值操作符5.三元运算符三、总结一、前言 当我们在编写Flutter应用程序时,操作符是我们不可或缺的工具。它们是用于执行各种操作的关键字和符号,可以帮助我们简化代码并提高效率。熟练掌握各种类型…...
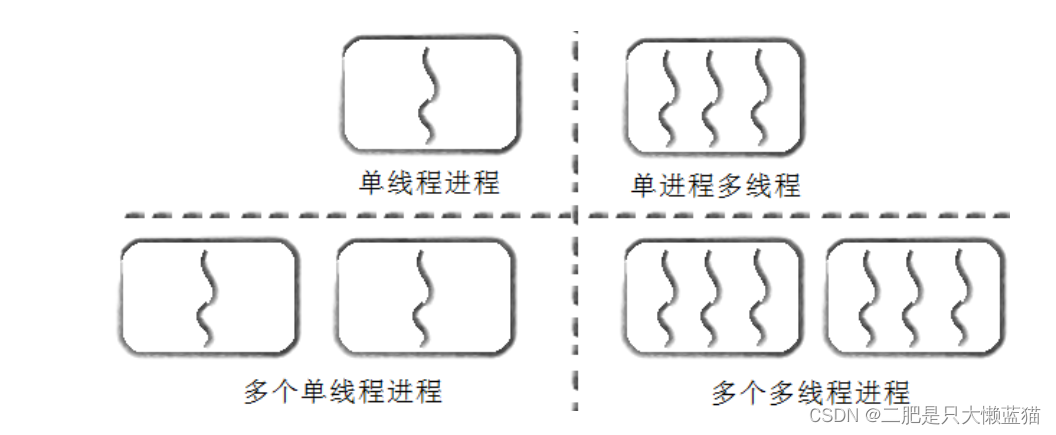
Linux线程概念
重新认识一下进程 在之前写过的与进程相关的博文中,都把进程看作是只有一个PCB的进程。如图: 而实际上,在Linux中,进程不止一个执行流,而是可能会有几个或很多个。同一个进程中,每一个执行流都指向同一个虚…...

C#基础教程10 方法
C#方法 方法的语法访问修饰符:返回类型:方法名称:参数列表:方法体:返回值:方法的调用参数传递按值传递按引用传递输出参数方法的重载总结方法是C#中最基本的代码结构之一。方法是一组可重复使用的代码,它接受输入,执行一些操作并返回结果。在本教程中,我们将深入了解C…...
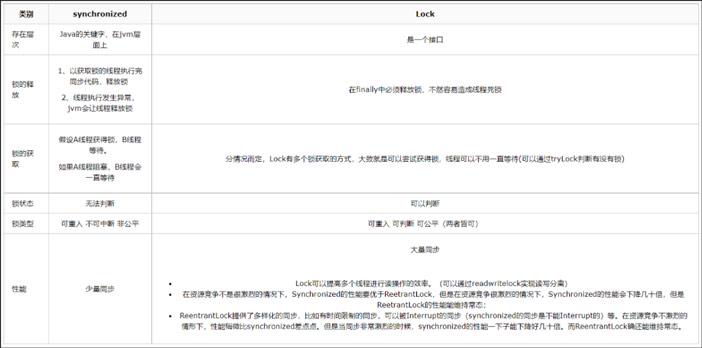
java高性能并发计数器之巅峰对决
并发计数器各个方案介绍方案概述1. jdk5提供的原子更新长整型类 AtomicLong2. synchronized3. jdk8提供的 LongAdder 【单机推荐】4. Redisson分布式累加器【分布式推荐】方案介绍jdk5提供的原子更新长整型类 AtomicLong在JDK1.5开始就新增了并发的Integer/Long的操作工具类Ato…...

HTTPS简介
HTTPS是HTTP开启TLS传输协议,客户端要拿到服务端的公钥,用公钥加密数据后再进行传输,防止数据泄露后背篡改。它要解决两个问题:怎么保证公钥可信怎么加密数据公钥可信问题客户端从服务端获取公钥的时候,存在请求被拦截…...

K-means聚类
原理说明 Kmeans是一种常见的聚类算法,用于将相似的数据点归类到不同的群组中。Kmeans的原理如下: 初始化:Kmeans算法首先需要初始化一个用户指定数量的聚类中心点,通常是随机选取K个数据点作为聚类中心点。 分配:对…...

04-SQL基础(表管理,约束,多表连接,子查询)
本文章主要内容 1、表的管理:创建表,修改表结构,删除字段,修改字段,添加字段,删除表,添加表约束; 2、数据管理:新增记录,修改记录,删除记录&…...
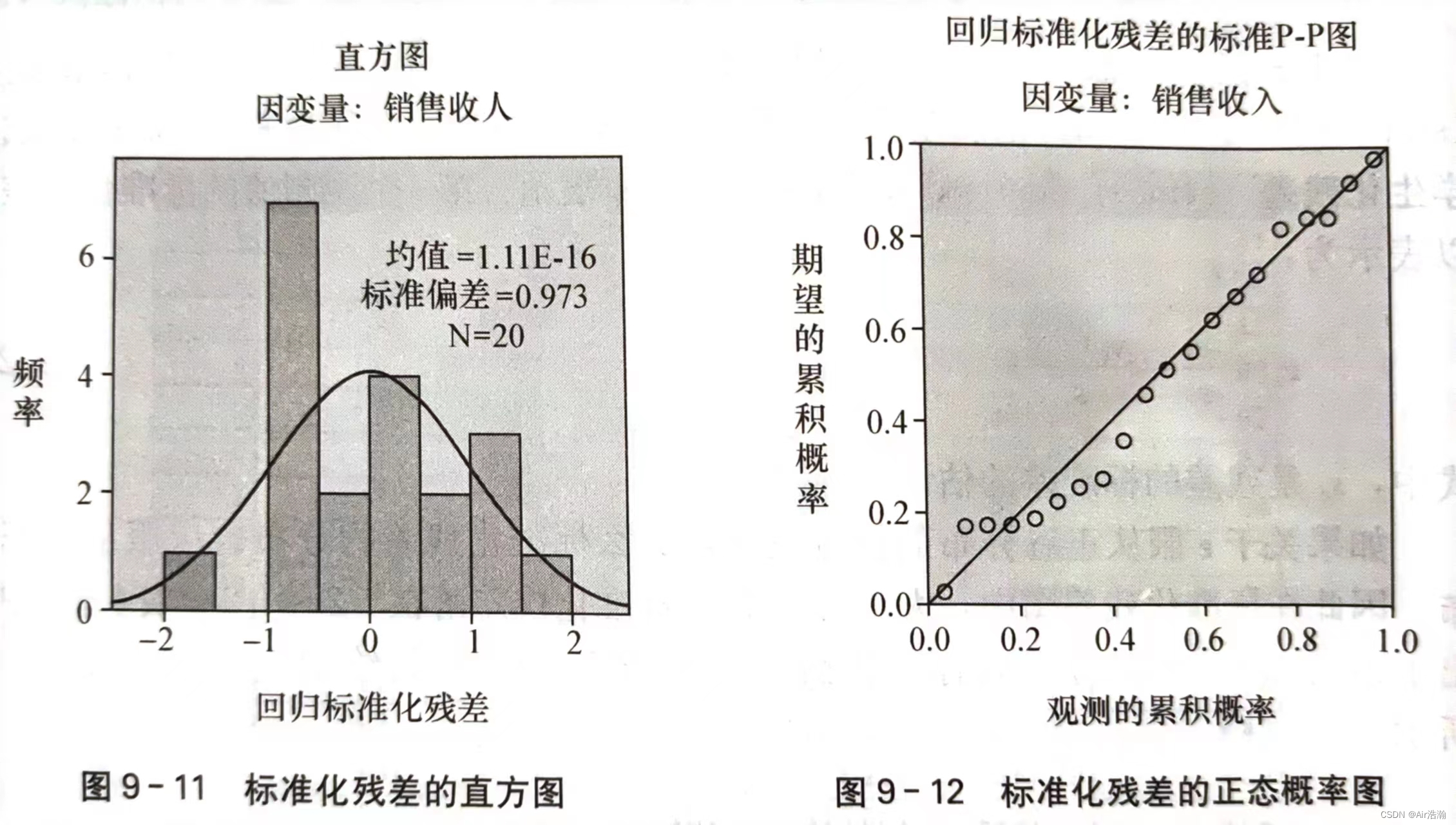
统计学 一元线性回归
统计学 一元线性回归 回归(Regression):假定因变量与自变量之间有某种关系,并把这种关系用适当的数学模型表达出来,利用该模型根据给定的自变量来预测因变量 线性回归:因变量和自变量之间是线性关系 非线…...

【软件开发】基于PyQt5开发的标注软件
这里是基于PyQt5写的面向目标检测的各类标注PC端软件系统。目前现有的labelme软件和labelImg开源软件无法满足特殊数据集的标注要求,而且没有标注顺序的报错提示。当然我设计的软件就会不具有适用性了(毕竟从下面开发的软件可以明显看出来我做的基本上是…...

CSS3新特性
CSS3新特性前言css3选择器边框特性背景参考前言 css3作为css的升级版本,css3提供了更加丰富实用的规范。新特性有: css3选择器边框特性多背景图颜色与透明度多列布局与弹性盒模型布局盒子的变形过渡与动画web字体媒体查询阴影 css3选择器 css3选择器…...

35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
文章目录35 openEuler搭建repo(yum)服务器-创建、更新本地repo源35.1 获取ISO发布包35.2 挂载ISO创建repo源35.3 创建本地repo源35.4 更新repo源35 openEuler搭建repo(yum)服务器-创建、更新本地repo源 使用mount挂载,…...
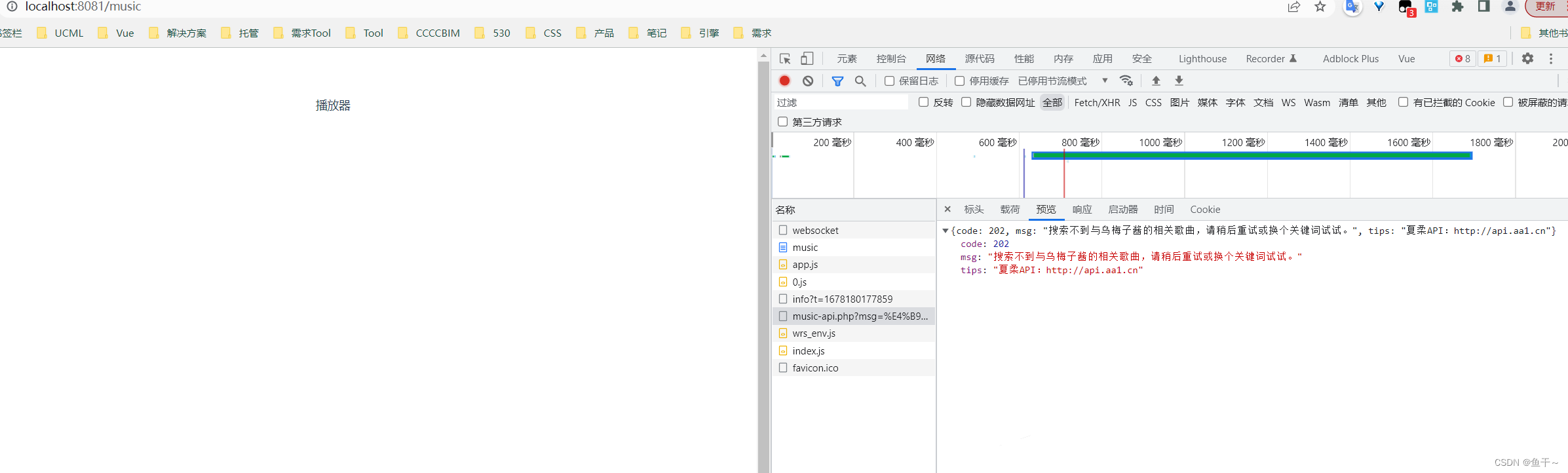
【三.项目引入axios、申明全局变量、设置跨域】
根据前文《二.项目使用vue-router,引入ant-design-vue的UI框架,引入less》搭建好脚手架后使用 需求: 1.项目引入axios 2.申明全局变量 3.设置跨域 简介:axios本质上还是对原生XMLHttpRequest的封装,可用于浏览器和nodejs的HTTP客…...

启动u盘还原成普通u盘(Windows Diskpart)
使用windows系统的diskpart 命令解决系统盘恢复成普通U盘的问题:1. 按Windows R键打开运行窗口。在搜索框中输入“ Diskpart ”,然后按 Enter 键。2. 现在输入“ list disk ”并回车。3. 然后输入“ select disk X ”(将 X 替换为可启动U盘的…...
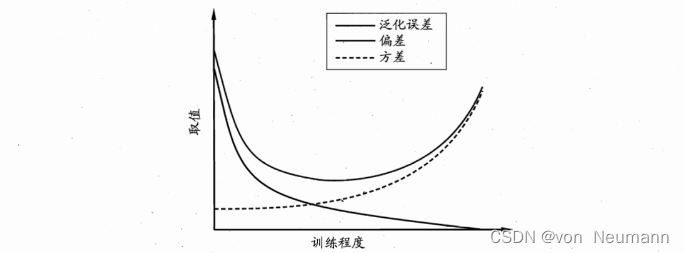
深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录 偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学…...

分布式新闻项目实战 - 13.项目部署_持续集成(Jenkins) ^_^ 完结啦 ~
欲买桂花同载酒,终不似,少年游。 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)自媒体文章审核延迟任务kafka及文章上下架App端文章搜索后台系统管理Long类型精度丢失问题定时计算热点文章(xxl-Job…...

Linux c/c++技术方向分析
一、C与C介绍 1.1 说明 c语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发,如嵌入式。C语言能以简易的方式编译、处理低级存储器。是一种高效率程序设计语言。 c(c plus plus)是一种计算机高级程序设计语言&a…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
