蓝桥杯gcd汇总
gcd3014
问题描述
小明和小红是一对恋人,他们相爱已经三年了,在今年的七夕节,小明准备给小红一个特殊的礼物。他想要送给小红一些数字,让小红算出有多少对正整数 (a,b) 满足以下条件:
c×lcm(a,b)−d×gcd(a,b)=x其中 c,d,x 是小明给出的数gcd(a,b) 为 a,b 的最大公因lcm(a,b) 为 a,b 的最小公倍数 。
小明希望这个问题能够考察小红对于数论基础知识的理解和运用,同时也希望小红能够在这个特殊的日子里感受到他对她的深情。请你帮助小明实现他的想法吧!
输入格式
第一行包含一个正整数 T(1≤T≤103),表示询问的组数。
接下来 T 行,每行包含三个正整数 c,d,x(1≤c,d,x≤105)。
输出格式
对于每组询问,输出一个正整数表示满足条件的(a,b) 对数。
样例输入
2
2 3 6
4 5 7
样例输出
4
2解析
需要理解gcd(最大公因数)和lcm(最小公倍数)的性质,并且能够遍历所有可能的正整数对(a, b),计算满足条件的数量。然而,直接遍历所有可能的(a, b)对会导致时间复杂度过高,因此我们需要观察题目中所给的不等式。
代码
package lanqiaoyun; import java.util.*; public class gcd3014 {public static void main(String args[]) {Scanner scanner=new Scanner(System.in);int T = scanner.nextInt();while (T-- > 0) {int c = scanner.nextInt();int d = scanner.nextInt();int x = scanner.nextInt();System.out.println(countPairs(c, d, x));}scanner.close();}private static int countPairs(int c, int d, int x) {int count = 0;// gcd中所有的可能的元素for (int g = 1; g * g <= x; g++) {if (x % g != 0) continue; // Skip if g does not divide xint n = (x + d * g) / c; // 计算a*bif (n % g != 0) continue; // Skip if g does not divide nint phi = eulerPhi(n / g); // Calculate phi(n/g), the count of numbers coprime with n/gcount += phi; // Add phi(n/g) to the count for each valid g}return count;}// Calculate Euler's totient function phi(n)private static int eulerPhi(int n) {int result = n;for (int i = 2; i * i <= n; i++) {if (n % i == 0) {while (n % i == 0) {n /= i;}result -= result / i;}}if (n > 1) {result -= result / n;}return result;}public static long gcd(long a,long b) {return b==0?a:gcd(b,a%b);}public static long lcm(long a,long b) {return a/gcd(a,b)*b;} }
gcd368
在社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果。例如,对某一观点表示支持的有 1498 人,反对的有 902 人,那么赞同与反对的比例可以简单的记为 1498:902。
不过,如果把调查结果就以这种方式呈现出来,大多数人肯定不会满意。因为这个比例的数值太大,难以一眼看出它们的关系。对于上面这个例子,如果把比例记为 5:3,虽然与真实结果有一定的误差,但依然能够较为准确地反映调查结果,同时也显得比较直观。
现给出支持人数 A,反对人数 B,以及一个上限 L,请你将 A 比 B 化简为 ′A′ 比 ′B′,要求在 ′A′和 ‘B′均不大于 L 且 ′A′和 ′B′互质(两个整数的最大公约数是 1)的前提下,A′/B′≥A/B且A′/B′−A/B 的值尽可能小。
输入描述
输入共一行,包含三个整数 A,B,L,每两个整数之间用一个空格隔开,分别表示支持人数、反对人数以及上限。
其中,1≤A≤106,1≤B≤106,1≤L≤100,A/B≤L。
输出描述
输出共一行,包含两个整数 ′A′,B′,中间用一个空格隔开,表示化简后的比例。
输入输出样例
示例
输入
1498 902 10
输出
5 3代码
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);//在此输入您的代码...double a=scan.nextDouble();double b=scan.nextDouble();double l=scan.nextDouble();double min=100;int res1=0;int res2=0;for(int i=0;i<l;i++){for(int j=1;j<l;j++){double m=(double) a*1.0/b;double p=(double) i*1.0/j;if(p>=m&&gcd(i,j)==1&&p-m<=min){min=(p-m);//持续寻找更小的min,并更新res1=i;res2=j;}}}if(l==1) {res1=1;res2=1;System.out.println(res1+" "+res2);}else {System.out.println(res1+" "+res2);}scan.close();}public static double gcd(double a,double b ){return b==0?a:gcd(b,a%b);}}gcd520
题目描述
Hanks 博士是 BT (Bio-Tech,生物技术) 领域的知名专家,他的儿子名叫 Hankson。现在,刚刚放学回家的 Hankson 正在思考一个有趣的问题。
今天在课堂上,老师讲解了如何求两个正整数c1 和 c2 的最大公约数和最小公倍数。现在 Hankson 认为自己已经熟练地掌握了这些知识,他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”,这个问题是这样的:已知正整数a0,a1,b0,b1,设某未知正整数 x 满足:
-
x 和 a0 的最大公约数是 a1;
-
x 和 b0 的最小公倍数是 b1。
Hankson 的“逆问题”就是求出满足条件的正整数 x。但稍加思索之后,他发现这样的 x 并不唯一,甚至可能不存在。因此他转而开始考虑如何求解满足条件的 x 的个数。请你帮助他编程求解这个问题。
输入描述
第一行为一个正整数 n,表示有 n 组输入数据。
接下来的 n 行每行一组输入数据,为四个正整数a0,a1,b0,b1,每两个整数之间用一个空格隔开。输入数据保证 a0 能被 a1 整除,b1 能被 b0 整除。
其中,保证有1≤a0,a1,b0,b1≤2×109且n≤2000。
输出描述
输出共 n 行。每组输入数据的输出结果占一行,为一个整数。
对于每组数据:若不存在这样的 x,请输出 0;若存在这样的 x,请输出满足条件的 x 的个数;
输入输出样例
示例 1
输入
2
41 1 96 288
95 1 37 1776
输出
6
2代码
package lanqiaoyun;
import java.util.*;
public class gcd520 {public static void main(String[] args) {// TODO Auto-generated method stubScanner scan = new Scanner(System.in);//在此输入您的代码...int n=scan.nextInt();while(n-->0){long a0=scan.nextLong();long a1=scan.nextLong();long b0=scan.nextLong();long b1=scan.nextLong();int count=0;for(int x=0;x<=b1;x++){if(gcd(x,a0)==a1&&lcm(x,b0)==b1){count++;}}System.out.println(count);}scan.close();}public static long gcd(long x,long a0){return a0==0?x:gcd(a0,x%a0);}public static long lcm(long x,long b0){return x/gcd(x,b0)*b0;}
}(后期持续更新)
相关文章:

蓝桥杯gcd汇总
gcd3014 问题描述 小明和小红是一对恋人,他们相爱已经三年了,在今年的七夕节,小明准备给小红一个特殊的礼物。他想要送给小红一些数字,让小红算出有多少对正整数 (a,b) 满足以下条件: clcm(a,b)−dgcd(a,b)x其中 c,…...
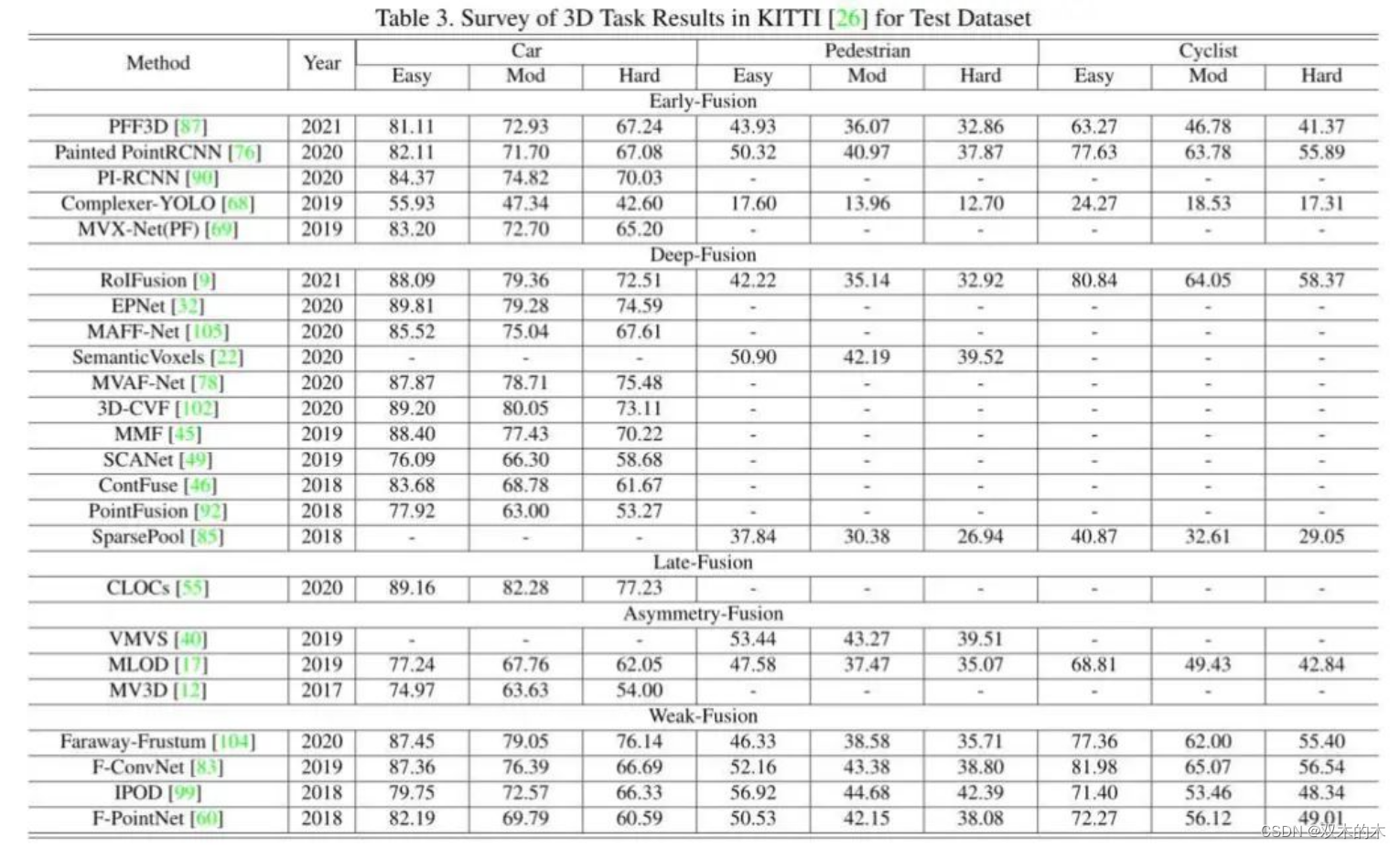
极市平台 | 综述:一文详解50多种多模态图像融合方法
本文来源公众号“极市平台”,仅用于学术分享,侵权删,干货满满。 原文链接:综述:一文详解50多种多模态图像融合方法 0 极市导读 本工作总结了50篇论文中Lidar和camera的多模态融合的一些概念方法。笔者结合原文以及自…...

数据结构系列-队列的结构和队列的实现
🌈个人主页:羽晨同学 💫个人格言:“成为自己未来的主人~” 队列 队列的概念及结构 队列:只允许在一端进行插入数据操作,在另一端进行删除删除数据操作的特殊线性表,队列具有先进先出FIFO,…...

MySQL——查询数据的处理
一、并列 连接两个数据列的值,并进行输出的格式化处理(显示为一种统一的格式) concat( 列 1 格式化字 符 ) mysql> select concat(vend_name, vend_country) from vendors; --------------------------------- | concat(vend_name, ve…...
【机器学习300问】59、计算图是如何帮助人们理解反向传播的?
在学习神经网络的时候,势必会学到误差反向传播,它对于神经网络的意义极其重大,它是训练多层前馈神经网络的核心算法,也是机器学习和深度学习领域中最为重要的算法之一。要正确理解误差反向传播,不妨借助一个工具——计…...

ctfshow web入门 php特性 web108--web115
web108 ereg函数相当于而preg_match()函数 ereg函数的漏洞:00截断。%00截断及遇到%00则默认为字符串的结束 strrev函数就是把字符串倒过来 就是说intval处理倒过来的传参c0x36d(877)?ca%00778 web109 异常处理类 通过异常处理类Excepti…...
京东API接口采集商品详情数据(测试入口如下)
京东API接口采集商品详情数据 请求示例,API接口接入Anzexi58 在当今数字化时代,电商平台的API接口成为了获取商品详情数据的重要途径之一。作为中国最大的自营式电商企业,京东提供了丰富的API接口供开发者使用,以便获取京东平台上…...

Mac brew 安装软件
Mac brew 安装软件 homebrew 速度慢 将brew 切换到国内镜像源 # 速度一般 # 步骤一 cd "$(brew --repo)" git remote set-url origin https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git# 步骤二 cd "$(brew --repo)/Library/Taps/homebrew/homebr…...

【顶部距离计算】计算元素顶部与浏览器顶部的距离
在开发中,我们常常需要计算某个元素顶部与浏览器视口顶部的距离,只需要一个方法即可计算 解决:使用getBoundingClientRect()方法 代码示例: 接收一个参数element表示需要计算的元素 // 计算该元素的顶部距离浏览器的顶部距离 c…...

守护人类健康:人工智能赋能医疗领域创新应用
编者按:每年的4月7日是世界卫生日,又称世界健康日,旨在引起世界各国人民对卫生、健康工作的关注,提高人们对卫生领域的素质和认识,强调健康对于劳动创造和幸福生活的重要性。那么,如果医疗技术能够更加智能…...
——cat、more、cp)
linux常用指令(一)——cat、more、cp
cat命令: 用于查询看文件内容 语法:cat linux路径 参数必填,表示要查看文件的目录的路径,(相对,绝对,特殊路径符都可以使用) more命令: 用于查看文件内容,…...
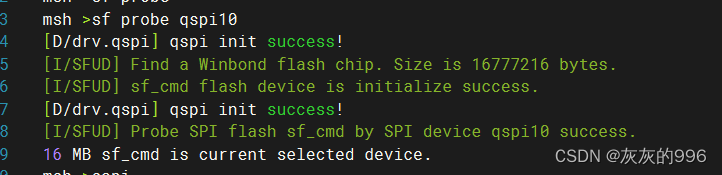
基于RTThread的学习(三):正点原子潘多拉 QSPI 通信 W25Q128 实验
1、基于芯片创建工程 2、QSPI配置 2.1、RTThing_setting 设置组件 2.2、配置board.h 文件 2.3、cubemx生成QSPI的硬件初始化代码;HAL_QSPI_MapInit; 这里注意:你所买的开发板对应的qspi 连接的是否是cubemx 上边显示的,如果不是你需要将引脚…...
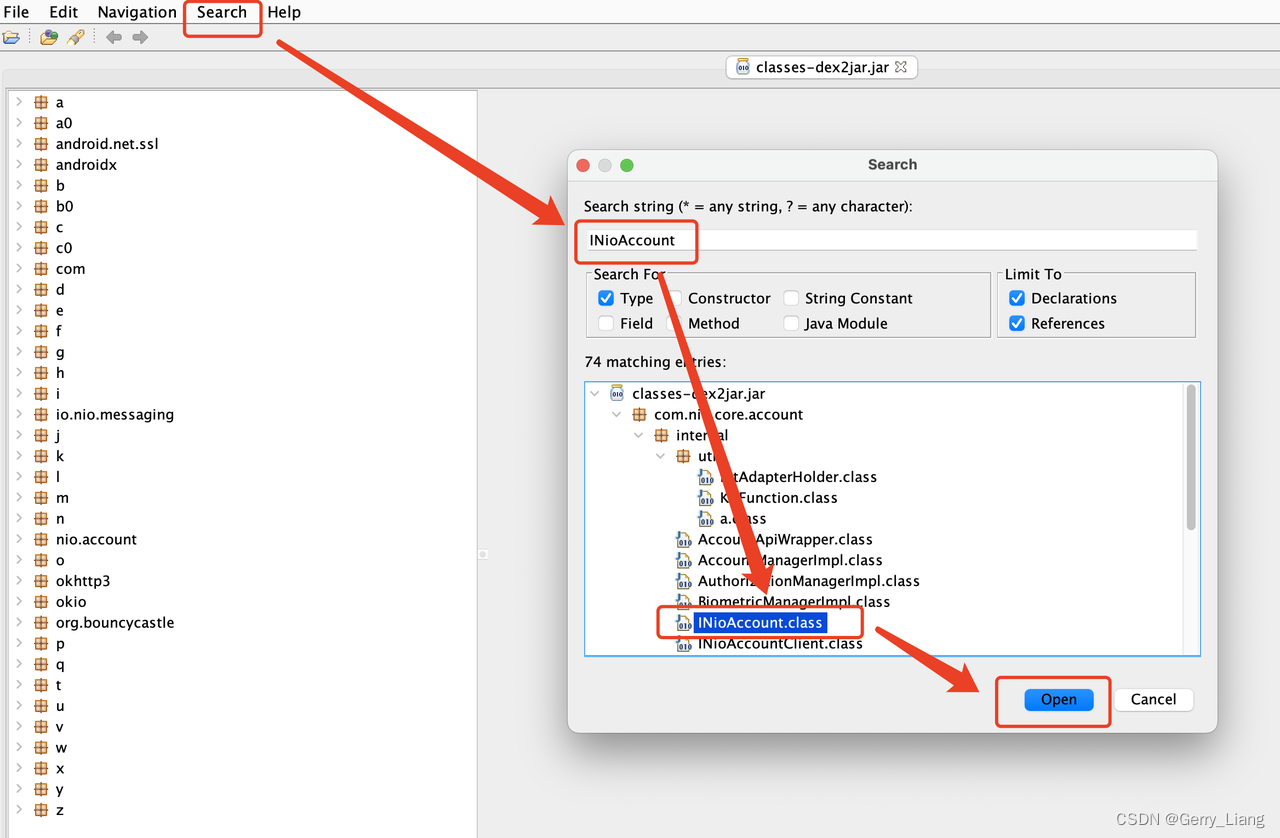
Mac反编译APK
文章目录 第一种方式: brew installapktool 使用说明dex2jar 使用说明 第二种方式: 下载安装包apktool 使用说明 (根据官方介绍没有操作成功,后续成功再更新这里)dex2jar 使用说明 安装 JD-GUI 查看jar包中的class文件JD-GUI 使用说明 第一种方式: brew install 安装过程可能很…...

Java数据结构-队列
目录 1. 队列概念2. 模拟实现队列2.1 链式队列2.2 循环队列 3. 双端队列4. 队列的应用4.1 用队列实现栈4.2 用栈实现队列 1. 队列概念 队列是一种只能在一端进行插入数据操作,另一端进行删除数据操作的数据结构,插入数据的叫队尾,删除数据的…...

JVM专题——类文件结构
本文部分内容节选自Java Guide和《深入理解Java虚拟机》, Java Guide地址: https://javaguide.cn/java/jvm/class-file-structure.html 🚀 基础(上) → 🚀 基础(中) → 🚀基础(下&am…...

零基础10 天入门 Web3之第2天
10 天入门 Web3之第2天Web3 是互联网的下一代,它将使人们拥有自己的数据并控制自己的在线体验。Web3 基于区块链技术,该技术为安全、透明和可信的交易提供支持。我准备做一个 10 天的学习计划,可帮助大家入门 Web3: 一、这是第二…...
Vue和FastAPI实现前后端分离
前言 近期接触了一些开源大模型应用服务,发现很多用的都是FastAPI web框架,于是乎研究了一下它的优势,印象最深有两个:一个是它的异步处理性能比较好,二是它可以类似java swagger的API交互文档,这个对应前…...

34470A是德科技34470A数字万用表
181/2461/8938产品概述: Truevolt数字万用表(34460A、34461A、34465A、34470A)利用是德科技的新专利技术,使您能够快速获得见解、测量低功耗设备并保持校准的测量结果。Truevolt提供全方位的测量能力,具有更高的精度、…...

iOS 开发中上传 IPA 文件的方法(无需 Mac 电脑
引言 在 iOS 开发中,将 IPA 文件上传到苹果开发者中心是一个重要的步骤。通常情况下,我们需要使用 Mac 电脑上的 Xcode 或 Application Loader 工具来完成这个任务。然而,如果你没有 Mac 电脑,也没有关系,本文将介绍一…...
c语言多媒体文件管理及检索系统220
定制魏:QTWZPW,获取更多源码等 目录 选题 程序设计题1:基于数据分析的小区电量扩容推荐程序 程序设计题2:神气的盒子 程序设计题3:多媒体文件管理及检索系统 程序设计题4: 计算24点游戏 程序设计题…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
