【机器学习300问】59、计算图是如何帮助人们理解反向传播的?
在学习神经网络的时候,势必会学到误差反向传播,它对于神经网络的意义极其重大,它是训练多层前馈神经网络的核心算法,也是机器学习和深度学习领域中最为重要的算法之一。要正确理解误差反向传播,不妨借助一个工具——计算图。
一、计算图是什么?
(1)计算图的定义
计算图是一种用来表示数学表达式和计算流程的数据结构(有向图),是一个将复杂计算过程可视化的图形模型。计算图中有节点(vertices)和边(edges)的概念,节点通常表示计算操作或者函数,而边表示数据或参数的流动,一个节点的输出可以成为另一个节点的输入。
(2)举例说明
举例说明一下,假设有这样一个数据表达式 它的计算图可以画成这样:

现在,在这个操作的前后分别再加上个操作 和
,那么这个新的复杂一点的计算图可以画成这样:
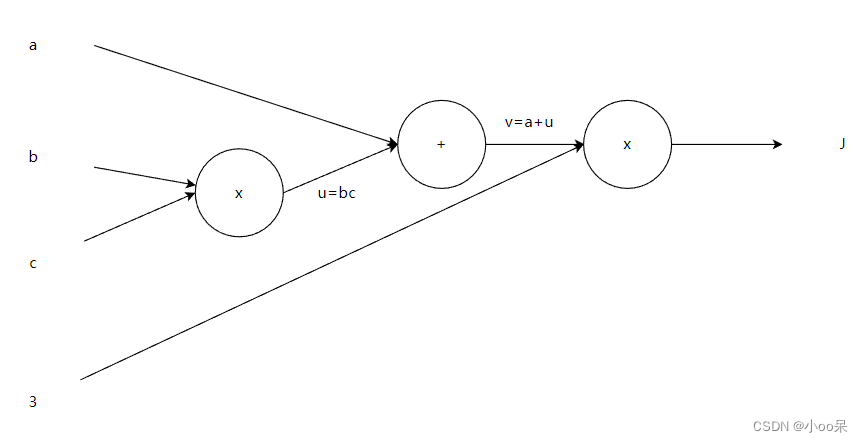
(3)计算图的主要用途和优点
① 直观的表现计算关系
计算图中的节点代表数值或者变量,而边则表示节点之间的依赖关系,例如加法、乘法或其他复杂操作。这种图形化的表示方式直观展示了计算步骤及其顺序。
② 进行局部计算
无论全局计算是多么的复杂,都可以通过局部计算使各个节点致力于简单的计算,从而简化问题。
③ 内存优化和提升计算效率
计算图可以缓存中间计算结果,避免重复计算,提高内存使用效率和减少运行时间。
④ 自动微分和计算梯度
在训练神经网络时,需要计算损失函数相对于所有权重的梯度来进行优化。计算图能够轻松实现自动微分,因为每一步计算的梯度可以通过链式法则从输出反向传播至输入,这一过程被称为反向传播。
二、计算图怎么实现正向传播?
(1)正向传播的过程
- 初始化节点值:在计算图中,输入层的每一个节点都会被赋予一个初始值,这通常是实际输入数据,比如一组特征向量。
- 应用权重和偏置:在计算到达隐藏层之前,输入层的节点值与对应的权重(weights)相乘。此外,每个隐藏层节点都会加上一个偏置值(bias)。这个操作对应计算图中的一个节点,其上一层的所有输出都会汇聚到这个点。
- 激活函数:在隐藏层节点加上权重和偏置之后,通过一个激活函数(如ReLU或Sigmoid)来引入非线性。激活函数的选择对网络的性能有着直接影响。此操作通常在计算图中表示为另外一个节点。
- 传递到下一层:经过激活函数处理后的值被传递到下一层,如果有多个隐藏层,则这一过程会重复进行,直到达到输出层。
- 输出层的计算:最后,当信息流到达输出层,相同的过程(加权、求和、添加偏置以及激活)会得到一个输出值。在分类任务中,这个值通常会通过softmax函数被转换成概率分布。
- 得出预测结果:这个最终经过激活处理的输出层的值就是网络的预测结果。对于不同的任务,比如分类、回归或其他,输出层会以不同的方式处理这些值来适应特定任务的需求。
(2)正向传播举例
以逻辑回归任务为例,来介绍一下上述过程的具体实现。先把逻辑回归所用到的公式说明一下:
假设数据样本只有两个特征和
,为了计算
,我们需要输入参数
,因此
的公式如上所示。逻辑回归模型的公式定义如下,其中
是预测值,
是sigmoid函数:
逻辑回归的损失函数定义如下,为了简单理解我给出的是单个样本的代价函数:
其中,a是逻辑回归的输出,y是样本的标签值(真实值)。现在我们画出这个计算图。

(3)人话理解正向传播
正向传播很好理解,就是你把数值带入上面这个图,从左向右正向一次计算每一个节点中的数学表达式,就得到了最终的输出。 虽然很好理解,但我在这里特意说明一下,在正向传播过程中,“传播”的实际上是信号数据(就是你通过节点式子算出来的值)。
中间怎么算的你可以忽略,正向传播就是在干这样一件事情,输入一组样本加上对应权重和偏置,得到一个最终的损失函数值。进一步理解就是说,不同的一组样本+权重+偏置会得到不同的损失函数值。因为神经网络学习的目的就是得到最优的权重和偏置(w,b合称参数),所以我把每次输入的训练样本都设成一样,但是允许更换许多许多组不同的权重+偏置的组合,就会得到许多许多不同的损失函数值。
我想要做的事情就是想得知:当损失函数值最小的时候,对应的权重+偏置是多少,此时的参数就是最优参数。要想达成这个目的就需要误差反向传播。
三、计算图怎么实现反向传播?
(1)反向传播的过程
计算图在实现反向传播的过程中扮演了关键角色,它提供了一种结构化的表示,使得能够高效且准确地计算神经网络中所有参数相对于损失函数的梯度。下面是利用计算图进行反向传播的基本步骤:
- 计算损失函数值:反向传播的起点是损失函数,使用预测结果和实际标签计算损失函数的值。损失函数衡量模型预测结果与真实值之间的差距。
- 初始化梯度:在损失节点处,对自身的梯度进行初始化,通常这个梯度是1,因为损失函数关于自身的导数是1。初始化所有参数(权重和偏置)的梯度为零。
- 利用链式法则计算每个节点梯度:从输出层开始,根据损失函数的梯度(即损失函数对输出层节点的导数),利用链式法则,将计算得到的梯度沿着计算图反向传播到每个权重和偏置。每个节点的梯度是其下游节点梯度与其本地导数的乘积累积而成。
- 梯度聚合:在计算图中,一个节点可能有多个输入,每个权重可能会受到多条路径上的梯度影响,需要将所有这些影响累积起来,得到最终的梯度值。
- 参数更新:当所有参数的梯度都通过反向传播计算出来后,根据优化算法(如梯度下降法或其变种)使用这些梯度来更新相应的权重和偏置。
(2)反向传播举例
以一个输入节点的输入层、一个sigmoid作为激活函数的隐藏层,一个输出节点的输出层为例。先给出他的正向传播计算图:
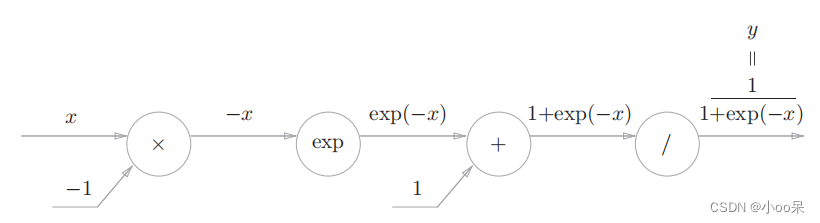
除了乘法和加法节点之外,还出现了自然数e为底的幂运算和除法节点。除法节点处的导数公式是:
反向传播时,会将上游的值乘上后再传给下游。计算图如下:
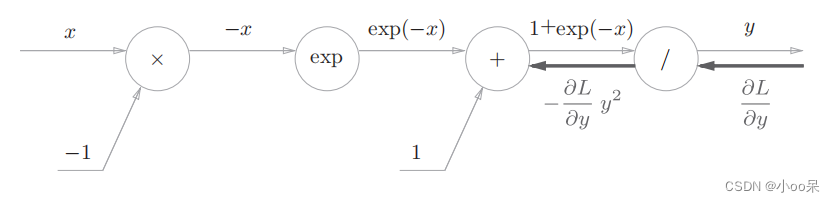
加法节点会原封不动的传给下游,计算图如下图所示:

exp节点的它的导数就是它自己,所以上游的值要乘上这个exp(-x)后再传给下游,计算图如下所示:
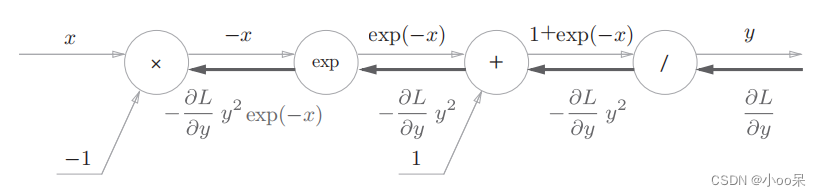
乘法节点将正向传播时的值翻转后做乘法,因此这里需要乘以-1,计算图如下所示:
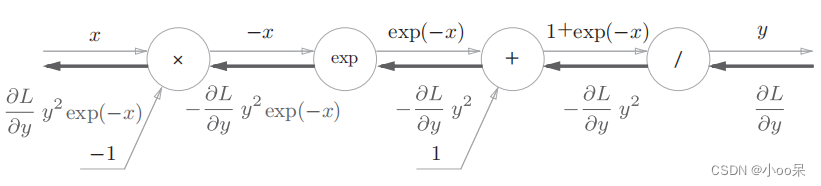
(3)人话理解反向传播
既然神经网络学习的目的是学到最优权重w和偏置b(合称参数),这个“最优”怎么定义?就是指能让损失函数值最小的参数,就是最优参数。要想得到最优参数,那么我就得回答这样一个问题,即怎么根据现在误差值来调整w和b才能让误差值变小呢?这个问题可以拆解成另外两个小问题:
① 误差和参数之间它们是怎么互相影响对方的?
建立参数与误差值之间的公式,也就是损失函数。通过损失函数就找到了他们之间的桥梁,就能知道误差想要表小,参数该如何变化。
② 如果误差变化了参数该如何变化?
为了使误差减小,我们需要根据损失函数关于参数的梯度来调整参数。梯度给出了损失函数在当前参数值处的斜率,指向损失函数值下降最快的方向。这里有必要重提一下导数的定义:“一函数在某一点的导数描述了这个函数在这一点附近的变化率”,也就是自变量变,函数值跟着变,还不是简单的跟着变多少,还知道变的快慢。假设我有三个参数,对损失函数求偏导就能知道每一个参数,它对应要变化多快或多慢,将这种变化率
反向传给原来的
,就能指导参数变化的具体值:
所以反向传播,“传播”的是误差信号在神经网络中的梯度(就是指导参数该怎么变的变化率)。具体来说,它并不是传播实际的输入数值或预测结果,而是传播从输出层到输入层的损失函数相对于网络中每个参数的梯度(梯度就是偏导数的向量表示)。这些梯度信息表明了在当前参数设置下,损失函数增大或减小的趋势。也就是说,告诉我们应当如何调整权重和偏置才能降低损失函数的值。
③ 举个小孩儿做题的例子
反向传播就好比你正在教一个小孩做一道复杂的数学题。小孩做完题后,你会检查答案是否正确,如果不对,你会告诉他哪里错了,让他改正。在这个过程中:
-
正向传播:就像是小孩按照步骤一步步计算题目。比如说他要计算
(a+b) × c,他先算出a+b的结果,然后再把这个结果乘以c得到最后的答案。
-
损失函数:相当于你用来判断小孩答案对错的标准。如果他的答案离正确答案差很多,你就有一个衡量错误程度的“分数”。
-
反向传播:是你指导小孩如何改正错误的过程。假设他最后的答案错了,你会告诉他:“你计算的最后一步有问题,你需要知道是因为
c值没乘对还是前面a+b的结果就不对。”于是你从最后一个步骤开始,告诉小孩每一步对他最后答案的影响有多大(也就是计算梯度),这样他才能有针对性地调整自己的计算步骤,以便下次做得更好。
这里的关键就在于,你没有告诉他正确答案(也就是损失函数最小的时候对应的参数,有时候正确答案你自己都不知道),而是通过提示让他自己一步步去找到正确答案。
相关文章:
【机器学习300问】59、计算图是如何帮助人们理解反向传播的?
在学习神经网络的时候,势必会学到误差反向传播,它对于神经网络的意义极其重大,它是训练多层前馈神经网络的核心算法,也是机器学习和深度学习领域中最为重要的算法之一。要正确理解误差反向传播,不妨借助一个工具——计…...

ctfshow web入门 php特性 web108--web115
web108 ereg函数相当于而preg_match()函数 ereg函数的漏洞:00截断。%00截断及遇到%00则默认为字符串的结束 strrev函数就是把字符串倒过来 就是说intval处理倒过来的传参c0x36d(877)?ca%00778 web109 异常处理类 通过异常处理类Excepti…...
京东API接口采集商品详情数据(测试入口如下)
京东API接口采集商品详情数据 请求示例,API接口接入Anzexi58 在当今数字化时代,电商平台的API接口成为了获取商品详情数据的重要途径之一。作为中国最大的自营式电商企业,京东提供了丰富的API接口供开发者使用,以便获取京东平台上…...

Mac brew 安装软件
Mac brew 安装软件 homebrew 速度慢 将brew 切换到国内镜像源 # 速度一般 # 步骤一 cd "$(brew --repo)" git remote set-url origin https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git# 步骤二 cd "$(brew --repo)/Library/Taps/homebrew/homebr…...

【顶部距离计算】计算元素顶部与浏览器顶部的距离
在开发中,我们常常需要计算某个元素顶部与浏览器视口顶部的距离,只需要一个方法即可计算 解决:使用getBoundingClientRect()方法 代码示例: 接收一个参数element表示需要计算的元素 // 计算该元素的顶部距离浏览器的顶部距离 c…...

守护人类健康:人工智能赋能医疗领域创新应用
编者按:每年的4月7日是世界卫生日,又称世界健康日,旨在引起世界各国人民对卫生、健康工作的关注,提高人们对卫生领域的素质和认识,强调健康对于劳动创造和幸福生活的重要性。那么,如果医疗技术能够更加智能…...
——cat、more、cp)
linux常用指令(一)——cat、more、cp
cat命令: 用于查询看文件内容 语法:cat linux路径 参数必填,表示要查看文件的目录的路径,(相对,绝对,特殊路径符都可以使用) more命令: 用于查看文件内容,…...
基于RTThread的学习(三):正点原子潘多拉 QSPI 通信 W25Q128 实验
1、基于芯片创建工程 2、QSPI配置 2.1、RTThing_setting 设置组件 2.2、配置board.h 文件 2.3、cubemx生成QSPI的硬件初始化代码;HAL_QSPI_MapInit; 这里注意:你所买的开发板对应的qspi 连接的是否是cubemx 上边显示的,如果不是你需要将引脚…...
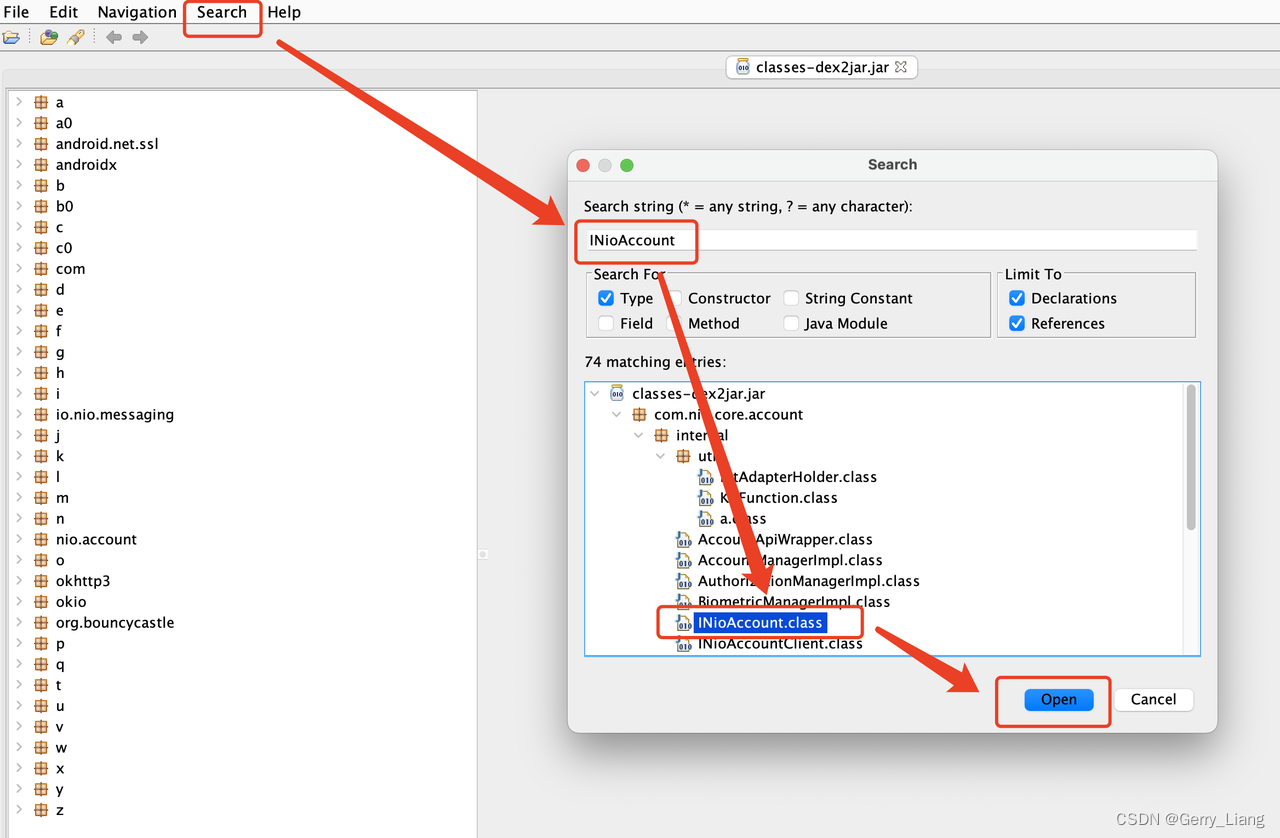
Mac反编译APK
文章目录 第一种方式: brew installapktool 使用说明dex2jar 使用说明 第二种方式: 下载安装包apktool 使用说明 (根据官方介绍没有操作成功,后续成功再更新这里)dex2jar 使用说明 安装 JD-GUI 查看jar包中的class文件JD-GUI 使用说明 第一种方式: brew install 安装过程可能很…...

Java数据结构-队列
目录 1. 队列概念2. 模拟实现队列2.1 链式队列2.2 循环队列 3. 双端队列4. 队列的应用4.1 用队列实现栈4.2 用栈实现队列 1. 队列概念 队列是一种只能在一端进行插入数据操作,另一端进行删除数据操作的数据结构,插入数据的叫队尾,删除数据的…...

JVM专题——类文件结构
本文部分内容节选自Java Guide和《深入理解Java虚拟机》, Java Guide地址: https://javaguide.cn/java/jvm/class-file-structure.html 🚀 基础(上) → 🚀 基础(中) → 🚀基础(下&am…...

零基础10 天入门 Web3之第2天
10 天入门 Web3之第2天Web3 是互联网的下一代,它将使人们拥有自己的数据并控制自己的在线体验。Web3 基于区块链技术,该技术为安全、透明和可信的交易提供支持。我准备做一个 10 天的学习计划,可帮助大家入门 Web3: 一、这是第二…...
Vue和FastAPI实现前后端分离
前言 近期接触了一些开源大模型应用服务,发现很多用的都是FastAPI web框架,于是乎研究了一下它的优势,印象最深有两个:一个是它的异步处理性能比较好,二是它可以类似java swagger的API交互文档,这个对应前…...

34470A是德科技34470A数字万用表
181/2461/8938产品概述: Truevolt数字万用表(34460A、34461A、34465A、34470A)利用是德科技的新专利技术,使您能够快速获得见解、测量低功耗设备并保持校准的测量结果。Truevolt提供全方位的测量能力,具有更高的精度、…...

iOS 开发中上传 IPA 文件的方法(无需 Mac 电脑
引言 在 iOS 开发中,将 IPA 文件上传到苹果开发者中心是一个重要的步骤。通常情况下,我们需要使用 Mac 电脑上的 Xcode 或 Application Loader 工具来完成这个任务。然而,如果你没有 Mac 电脑,也没有关系,本文将介绍一…...
c语言多媒体文件管理及检索系统220
定制魏:QTWZPW,获取更多源码等 目录 选题 程序设计题1:基于数据分析的小区电量扩容推荐程序 程序设计题2:神气的盒子 程序设计题3:多媒体文件管理及检索系统 程序设计题4: 计算24点游戏 程序设计题…...
链表之双向链表的实现
铁汁们大家好,我们上一篇博客学习了单链表,这节课让我们继续往深学习,学习一下双线链表,话不多说,我们开始吧! 目录 1.双向链表 2.顺序表和链表的优缺点 3.双向链表的实现 1.双向链表 1.我们要实现的双线…...

小白学大模型:什么是生成式人工智能?
什么是生成式人工智能? 在过去几年中,机器学习领域取得了迅猛进步,创造了人工智能的一个新的子领域:生成式人工智能。这些程序通过分析大量的数字化材料产生新颖的文本、图像、音乐和软件,我将这些程序简称为“GAIs”…...

并发编程01-深入理解Java并发/线程等待/通知机制
为什么我们要学习并发编程? 最直白的原因,因为面试需要,我们来看看美团和阿里对 Java 岗位的 JD: 从上面两大互联网公司的招聘需求可以看到, 大厂的 Java 岗的并发编程能力属于标配。 而在非大厂的公司, 并…...
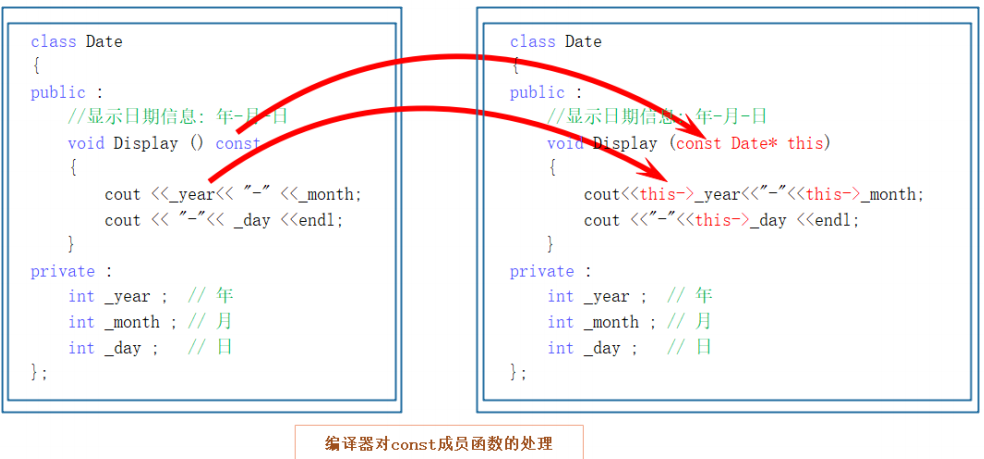
3.类与对象(中篇)介绍了类的6个默认构造函数,列举了相关案例,实现了一个日期类
1.类的6个默认成员函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,编译器会…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
