pytorch中的nn.MSELoss()均方误差损失函数
一、nn.MSELoss()是PyTorch中的一个损失函数,用于计算均方误差损失。
均方误差损失函数通常用于回归问题中,它的作用是计算目标值和模型预测值之间的平方差的平均值。
具体来说,nn.MSELoss()函数的输入是两个张量,即模型的真实值和预测值,输出是一个标量,表示两个张量之间的均方误差。在训练神经网络时,通常将该损失函数作为优化器的目标函数,通过反向传播算法来更新模型的参数,以最小化均方误差损失。
使用nn.MSELoss()函数时,通常需要传入两个参数:目标值和预测值。预测值可以是模型的输出值,目标值可以是训练集中的真实标签。
二、nn.MSELoss()的损失函数公式为:
MSE Loss = 1/N * sum( (target - output)² / 2)。
其中,N为batch size,即样本点的数量;target为真实值,即目标值;output为模型预测值,即模型的输出值。
这个公式表示对模型预测值与真实值之间的差距进行平方,并求取平均值,因此该损失函数可以衡量模型预测值与真实值之间的距离。通过最小化这个损失函数,可以优化模型的参数,使模型的预测值更接近真实值。
在PyTorch中,nn.MSELoss()函数用于计算均方误差损失,通常用于回归问题的模型训练和评估。需要注意的是,该函数会对输入的所有元素进行逐个计算,因此输入张量的形状需要匹配。
总之,nn.MSELoss()是一个常用的均方误差损失函数的实现,可以用于模型训练和评估。
相关文章:
均方误差损失函数)
pytorch中的nn.MSELoss()均方误差损失函数
一、nn.MSELoss()是PyTorch中的一个损失函数,用于计算均方误差损失。 均方误差损失函数通常用于回归问题中,它的作用是计算目标值和模型预测值之间的平方差的平均值。 具体来说,nn.MSELoss()函数的输入是两个张量,即模型的真实值…...

三国游戏(贪心 排序)
三国游戏 利用贪心、排序、前缀和的计算方法,特别注意不要数据溢出了,sum 加long long s[i] x[i]-y[i]-z[i]输入: 3 1 2 2 2 3 2 1 0 7输出: 2#include <bits/stdc.h> using namespace std;const int N 1e5100;typedef long long ll;bool cm…...

GPU环境安装与虚拟环境安装(适用于Windows下的李沐GPU)
之前我是用的都是VMware的虚拟机且安装的是cpu的pytorch版本,因为想要使用GPU,最终实现了在Windows上使用GPU,并且相关原理也在参考文章或视频内,可以通过原理自行挑选自己所需的配置并安装。 文章目录 1.GPU安装1.1 名词解释1.2 卸载旧版本的CUDA1.3 版本选择步骤(Nivida显卡…...

Http Download
Http / Https 下载文件,startWith不能验证https,测试地址:https://storage.googleapis.com/golang/go1.7.3.windows-amd64.msi private static final Logger logger Logger.getLogger(MethodHandles.lookup().lookupClass());private static…...

【Android】Glide加载SVG,SVG转PNG
Dependency plugins {id kotlin-kapt }dependencies {api com.github.bumptech.glide:glide:4.12.0kapt com.github.bumptech.glide:compiler:4.12.0api com.caverock:androidsvg:1.4 }SvgDecoder 负责解码SVG资源 import com.bumptech.glide.load.Options import com.bumpte…...

Spring、SpringMVC、Springboot三者的区别和联系
1.背景 最近有人问面试的一个问题:Spring、SpringMVC、Springboot三者的区别和联系,个人觉得:万变不离其宗,只需要理解其原理,回答问题信手拈来。 2.三者区别和联系 2.1 先了解Spring基础 Spring 框架就像一个家族…...

一点点安全资料:网络安全扩展
协议扩展 加密协议SSL/TLS 简介 SSL(Secure Sockets Layer)和TLS(Transport Layer Security)是加密协议,设计用来提供网络通信的安全性和数据完整性。尽管TLS是SSL的后继者,但两者的核心目标相同&#x…...
vscode的源码插件GitHub Repositories
打铁还需自身硬,需要不断提升自我,提升自我的一种方式就是看源码,站在更高的维度去理解底层原理,以便以后更好的开发和解决问题,由于源码一个动不动就是几个G甚至十几个G,如果一个个源码下载下来࿰…...

如何定义快速开发平台框架?有何突出优势?
作为提质增效的利器软件,快速开发平台框架如何能在众多同行中取胜?又是凭借什么优势特点在激烈的市场竞争中获得众多客户的青睐与信任?不管是从企业角度、服务商角度,还是使用者的角度来说,做好流程化进程,…...

二分练习题——奶牛晒衣服
奶牛晒衣服 题目分析 这里出现了“弄干所有衣服的最小时间”,那么可以考虑用二分去做。 第一阶段二段性分析 假设当前需要耗费的时间为mid分钟,如果mid分钟内可以烘干这些衣服,那么我们可以确定右边界大于mid的区间一定也可以。但是此时我…...

python工具包【1】 -- 不同操作系统路径转换
python工具包【1】 – 不同操作系统路径转换 以下的工具类的作用是根据不同的操作系统,将代码中的路径转换成适应操作系统的路径。 代码 import osclass Base_Tools_Cls:def BasePathConvert_func(self, path):根据不同的操作系统,将路径进行转换为不…...

JAVA中@FunctionalInterface 注解使用
FunctionalInterface是Java 8引入的一个注解,用于标记一个接口为函数式接口。函数式接口是指只有一个抽象方法(除了Object类中的默认方法如equals、hashCode等)的接口。在Java 8及以后版本中,函数式接口可以与lambda表达式配合使用…...
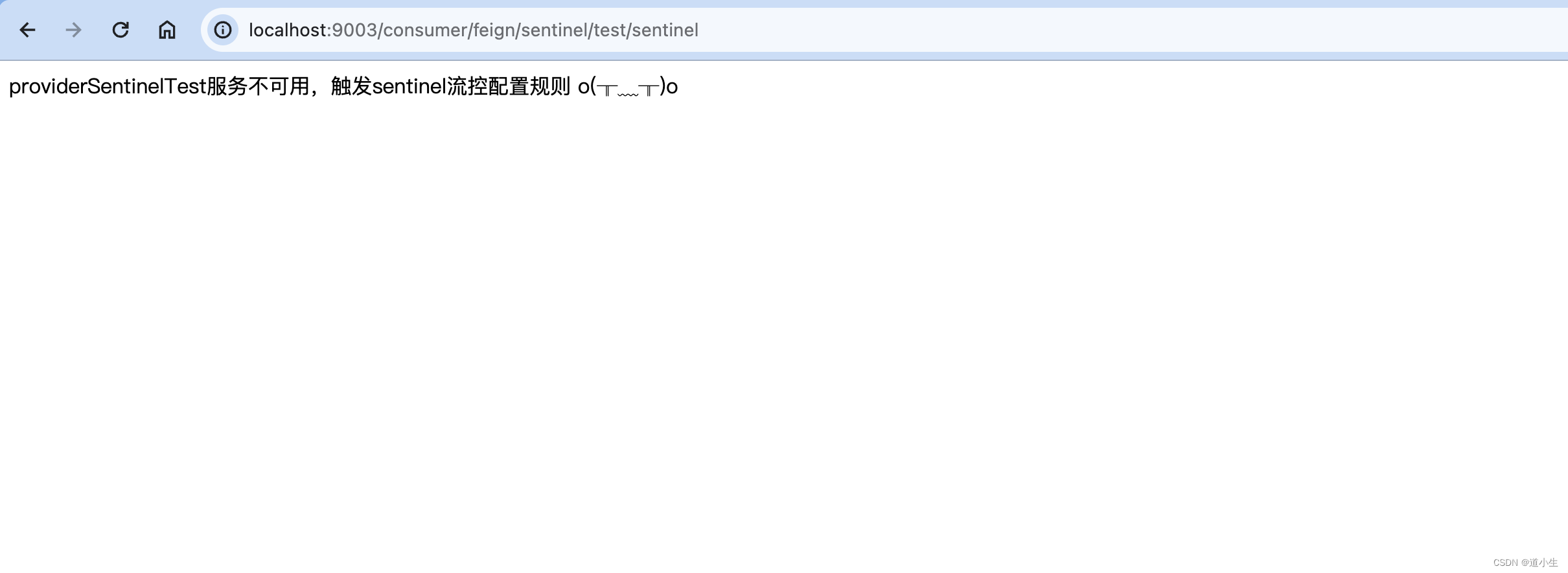
【Spring Cloud Alibaba】9 - OpenFeign集成Sentinel实现服务降级
目录 一、简介Sentinel 是什么如何引入Sentinel 二、服务搭建1.安装Sentinel控制台1.1 下载1.2 启动1.3 访问 2.改造服务提供者cloud-provider服务2.1 引入依赖2.2 添加API2.3 添加配置文件 3.改造cloud-consumer-feign服务3.1 引入依赖3.2 添加Feign接口3.3 添加服务降级类3.4…...

Chrome浏览器如何跟踪新开标签的网络请求?
在测试一个东西的时候,它虽然是a链接,但是,是由前端在js里写跳转的。我又必须要知道它的跳转链接,只能用截屏的方式来捕捉浏览器的地址栏链接 打开浏览器控制台(F12)点击红色箭头打钩为弹出式窗口自动打开DevTools 英文版调试参…...
html写一个登录注册页面
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>注册登录界面Ⅰ</title><link rel"stylesheet" href"https://cdnjs.cloudflare.com/ajax/libs/normalize/8.0.1/normalize.mi…...

Stable Diffusion|Ai赋能电商 Inpaint Anything
1. 背景介绍 随着人工智能技术的不断发展,其在电商领域的应用也越来越广泛。其中,图像修复技术在电商领域有着重要的应用价值。例如,在商品图片处理中,去除图片中的水印、瑕疵等,可以提高商品图片的质量和美观度。 2…...

启明智显M系列--工业级HMI芯片选型表
本章主要介绍启明智显M系列HMI主控芯片: 纯国产自主, RISC-V 内核,配备强大的 2D 图形加速处理器、PNG/JPEG 解码引擎、H.264解码;工业宽温,提供全开源SDK;1秒快速开机启动的特性,极大地提高了…...
C语言面试题之最小高度树
最小高度树 实例要求 1、给定一个有序整数数组,元素各不相同且按升序排列;2、编写一个算法,创建一棵高度最小的二叉搜索树;示例: 给定有序数组: [-10,-3,0,5,9],一个可能的答案是:[0,-3,9,-10,null,5],它…...

【随笔】Git 高级篇 -- 整理提交记录(上)cherry-pick(十五)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...
上门服务小程序|上门服务系统|上门服务软件开发流程
在如今快节奏的生活中,上门服务小程序的需求越来越多。它们向用户提供了方便、高效的服务方式,解决了传统服务行业中的很多痛点。如果你也想开发一个上门服务小程序,以下是开发流程和需要注意的事项。 1、确定需求:在开始开发之前…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

IP选择注意事项
IP选择注意事项 MTP、FTP、EFUSE、EMEMORY选择时,需要考虑以下参数,然后确定后选择IP。 容量工作电压范围温度范围擦除、烧写速度/耗时读取所有bit的时间待机功耗擦写、烧写功耗面积所需要的mask layer...
