二分练习题——奶牛晒衣服
奶牛晒衣服
题目分析
这里出现了“弄干所有衣服的最小时间”,那么可以考虑用二分去做。
第一阶段二段性分析
假设当前需要耗费的时间为mid分钟,如果mid分钟内可以烘干这些衣服,那么我们可以确定右边界大于mid的区间一定也可以。但是此时我需要找的是最短时间,那么mid一定比大于mid的值更小,所以大于mid的值我就不用管了,也就是我可以确定我能够舍弃掉mid右边的值。我还想要确定比mid更小的值是否也满足条件,所以我要在mid的左边继续二分。
if(check(mid)) {r = mid;}//因为mid是符合条件的,所以我要留着它,而不是r=mid-1
假设当前需要耗费的时间为mid分钟,如果mid分钟内不可以烘干这些衣服,那么我们可以确定右边界小于mid的区间一定也不可以。所以小于mid的值我就不用管了,也就是我可以确定我能够舍弃掉mid左边的值。我还想要找比mid更大的值是否可以满足条件,所以我要在mid的右边继续二分。
else {l = mid + 1;}//因为mid是不符合条件的,所以我不要留着它,而不是l=mid
综上该题满足二段性,可以用二分,二分的板子就不说了,接下来说一下check函数如何写。
第二阶段写check函数
check(mid)要实现的作用是检查能否在mid分钟内烘干这些衣服。对于一个衣服的湿度w[i],如果w[i]/a大于mid(注意这里要采用函数实现上取整的话,应该使用double类型,所以在java里使用函数实现上取整时,用 a ∗ 1.0 a*1.0 a∗1.0将整数类型转化为浮点数类型),就需要使用烘干机,使用的时间是(a[i]-mid*a)/b,a是自然烘干每分钟可以减少的湿度,b是烘干机烘干每分钟额外减少的湿度。因为烘干衣服不足1分钟也要按一分钟算,所以这里要上取整。
java
static boolean check(int mid){long s = 0;for (int i = 0; i < n; i++) {if (Math.ceil(w[i]/(a*1.0))>mid){s += Math.ceil((w[i]-a*mid)/(b*1.0));}}return s <= mid;
}
c++
//这里的w[i]+a-1和w[i] - a * x + b - 1,即比正常多出来的+a-1和+b-1都是为了实现上取整。
bool check(int x){long sum = 0;for (int i = 0; i < n; i ++){if ((w[i]+a-1) / a <= x)continue;sum += (w[i] - a * x + b - 1) / b;}if (sum <= x)return true;else return false;
}
第三阶段二分范围确定
烘干的时间最长就是不使用烘干机,自然风干需要a[i]分钟,而a[i]最大是1e9,所以l=0,r=1e9。
注意一个特殊情况,如果k=1,那么其实烘干机有和没有都一样,自然风干所需要的时间就是所有衣服中最大的湿度。
题目代码
#include <iostream>
#include <stdbool.h>
#define N 500010int n, a, b;
int w[N];bool check(int x){long sum = 0;for (int i = 0; i < n; i ++){if ((w[i]+a-1) / a <= x)continue;sum += (w[i] - a * x + b - 1) / b;}if (sum <= x)return true;else return false;
}
int main(){scanf("%d%d%d",&n, &a, &b);for (int i = 0; i < n; i ++){scanf("%d", &w[i]);}int l = 0;int r = 5e5 + 5;while (l < r){int mid = (l + r) / 2;if (check(mid))r = mid;elsel = mid + 1;}printf("%d", l);return 0;
}
import java.util.Scanner;
public class Main{static int a;static int b;static int n;static int[] w;public static void main(String[] args) {Scanner scan = new Scanner(System.in);n = scan.nextInt();w = new int[n];a = scan.nextInt();b = scan.nextInt();
// int max = a+b;for (int i = 0; i <n; i++) {w[i]= scan.nextInt();
// max= Math.max(max, w[i]);}int l = 0;int r = 500005;while (l<r){int mid=(l+r)/2;if(check(mid)){r=mid;}else {l=mid+1;}}System.out.println(l);}static boolean check(int mid){long s = 0;for (int i = 0; i < n; i++) {if (Math.ceil(w[i]/(a*1.0))>mid){s += Math.ceil((w[i]-a*mid)/(b*1.0));}}return s <= mid;}
}
相关文章:

二分练习题——奶牛晒衣服
奶牛晒衣服 题目分析 这里出现了“弄干所有衣服的最小时间”,那么可以考虑用二分去做。 第一阶段二段性分析 假设当前需要耗费的时间为mid分钟,如果mid分钟内可以烘干这些衣服,那么我们可以确定右边界大于mid的区间一定也可以。但是此时我…...

python工具包【1】 -- 不同操作系统路径转换
python工具包【1】 – 不同操作系统路径转换 以下的工具类的作用是根据不同的操作系统,将代码中的路径转换成适应操作系统的路径。 代码 import osclass Base_Tools_Cls:def BasePathConvert_func(self, path):根据不同的操作系统,将路径进行转换为不…...

JAVA中@FunctionalInterface 注解使用
FunctionalInterface是Java 8引入的一个注解,用于标记一个接口为函数式接口。函数式接口是指只有一个抽象方法(除了Object类中的默认方法如equals、hashCode等)的接口。在Java 8及以后版本中,函数式接口可以与lambda表达式配合使用…...
【Spring Cloud Alibaba】9 - OpenFeign集成Sentinel实现服务降级
目录 一、简介Sentinel 是什么如何引入Sentinel 二、服务搭建1.安装Sentinel控制台1.1 下载1.2 启动1.3 访问 2.改造服务提供者cloud-provider服务2.1 引入依赖2.2 添加API2.3 添加配置文件 3.改造cloud-consumer-feign服务3.1 引入依赖3.2 添加Feign接口3.3 添加服务降级类3.4…...

Chrome浏览器如何跟踪新开标签的网络请求?
在测试一个东西的时候,它虽然是a链接,但是,是由前端在js里写跳转的。我又必须要知道它的跳转链接,只能用截屏的方式来捕捉浏览器的地址栏链接 打开浏览器控制台(F12)点击红色箭头打钩为弹出式窗口自动打开DevTools 英文版调试参…...
html写一个登录注册页面
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>注册登录界面Ⅰ</title><link rel"stylesheet" href"https://cdnjs.cloudflare.com/ajax/libs/normalize/8.0.1/normalize.mi…...

Stable Diffusion|Ai赋能电商 Inpaint Anything
1. 背景介绍 随着人工智能技术的不断发展,其在电商领域的应用也越来越广泛。其中,图像修复技术在电商领域有着重要的应用价值。例如,在商品图片处理中,去除图片中的水印、瑕疵等,可以提高商品图片的质量和美观度。 2…...

启明智显M系列--工业级HMI芯片选型表
本章主要介绍启明智显M系列HMI主控芯片: 纯国产自主, RISC-V 内核,配备强大的 2D 图形加速处理器、PNG/JPEG 解码引擎、H.264解码;工业宽温,提供全开源SDK;1秒快速开机启动的特性,极大地提高了…...
C语言面试题之最小高度树
最小高度树 实例要求 1、给定一个有序整数数组,元素各不相同且按升序排列;2、编写一个算法,创建一棵高度最小的二叉搜索树;示例: 给定有序数组: [-10,-3,0,5,9],一个可能的答案是:[0,-3,9,-10,null,5],它…...

【随笔】Git 高级篇 -- 整理提交记录(上)cherry-pick(十五)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...
上门服务小程序|上门服务系统|上门服务软件开发流程
在如今快节奏的生活中,上门服务小程序的需求越来越多。它们向用户提供了方便、高效的服务方式,解决了传统服务行业中的很多痛点。如果你也想开发一个上门服务小程序,以下是开发流程和需要注意的事项。 1、确定需求:在开始开发之前…...

Vuex(vue 项目中实现 频繁、大范围数据共享的技术方案)
参考文档(点击查看) 好处 1.数据的存取一步到位,不需层层传递 2.数据的流动非常清晰 3.存储在Vuex中的数据都是响应式的(数据更新后,使用数据的组件都会自动更新) Vuex基础配置 npm i vuex3.6.2state中用来存储数据,…...

【Spring Cloud】服务容错中间件Sentinel入门
文章目录 什么是 SentinelSentinel 具有以下特征:Sentinel分为两个部分: 安装 Sentinel 控制台下载jar包,解压到文件夹启动控制台访问了解控制台的使用原理 微服务集成 Sentinel添加依赖增加配置测试用例编写启动程序 实现接口限流总结 欢迎来到阿Q社区 …...

算法刷题记录 Day36
算法刷题记录 Day36 Date: 2024.04.02 lc 416. 分割等和子集 //2. 一维数组 class Solution { public:bool canPartition(vector<int>& nums) {// 将问题转化为从数组中任意取数,使得容量为数组总和一半的背包内的价值尽可能大。// dp[j]表示容积为j的…...

面试必问 - CSS 中元素居中小技巧
在网页设计中,居中是一个至关重要的布局技巧,能够确保你的页面在不同设备和屏幕尺寸上呈现出优雅的样式。 在这篇文章中,将介绍一些 CSS 居中的基本技巧,适用于各种场景。 1. 水平居中 文本水平居中 通过设置 text-align: cen…...

Chatgpt润色论文
使用ChatGPT进行论文润色时的指令 1.英语学术润色 模板:Below is a paragraph from an academic paper. Polish the writing to meet the academic style,improve the spelling, grammar, clarity, concision and overall readability. When necessary, rewrite th…...
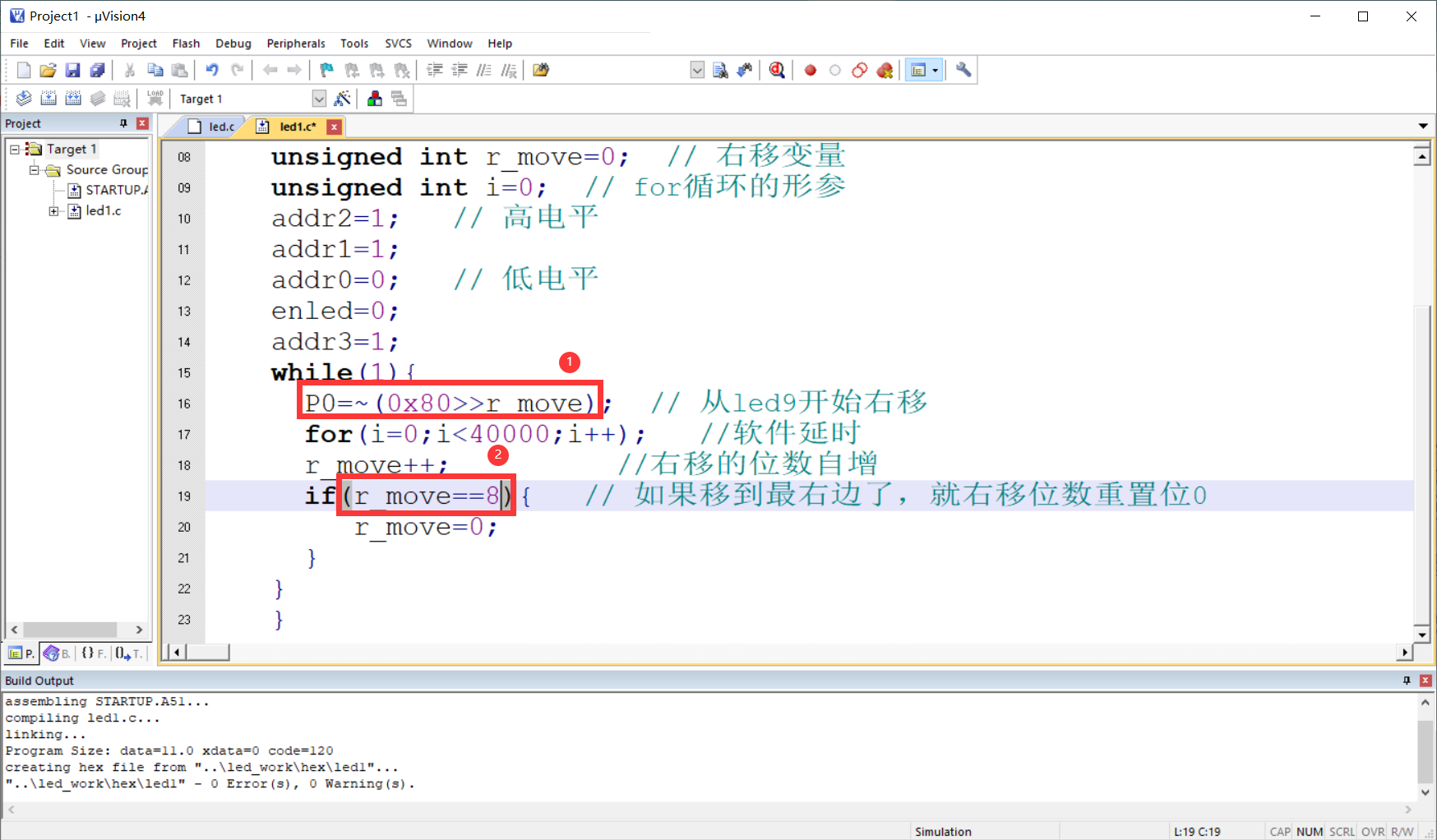
51单片机实验02- P0口流水灯实验
目录 一、实验的背景和意义 二、实验目的 三、实验步骤 四、实验仪器 五、实验任务及要求 1,从led4开始右移 1)思路 ①起始灯 (led4) ②右移 2)效果 3)代码☀ 2,从其他小灯并向右依…...
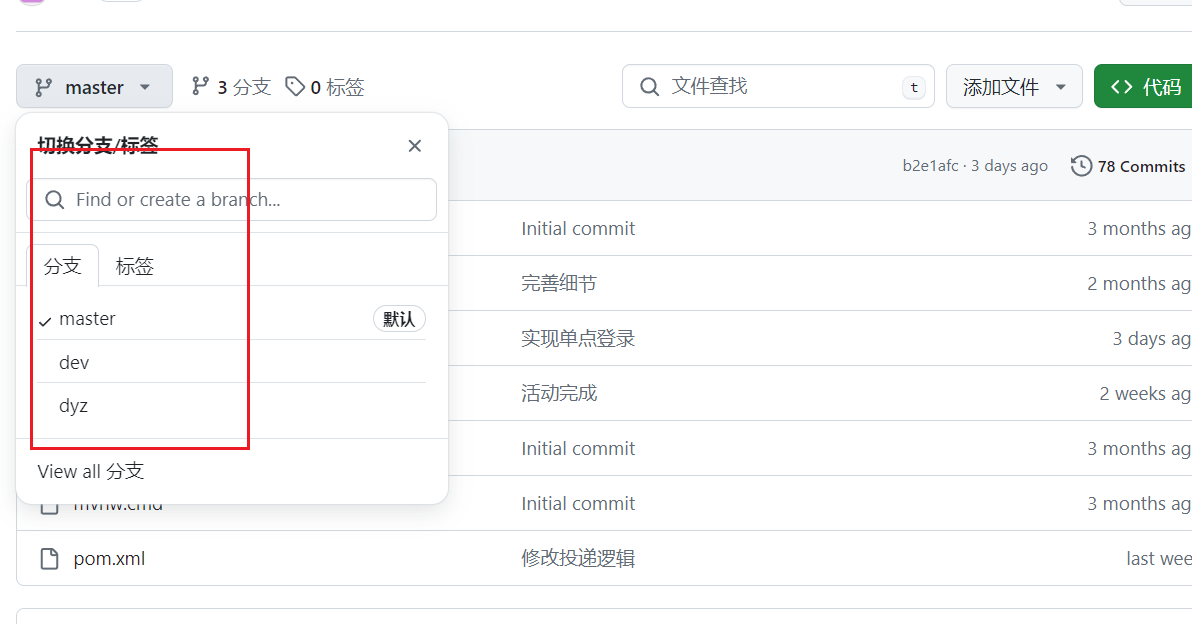
使用git 和 github协作开发
文章目录 github浏览器汉化插件github新建仓库git安装以及ssh配置团队创建及基本命令的使用创建团队基本命令 分支管理快速切换远程仓库地址 如何使用git && github进行协作开发,包括git常见基础命令 github浏览器汉化插件 在刚开始使用github的时候&#…...
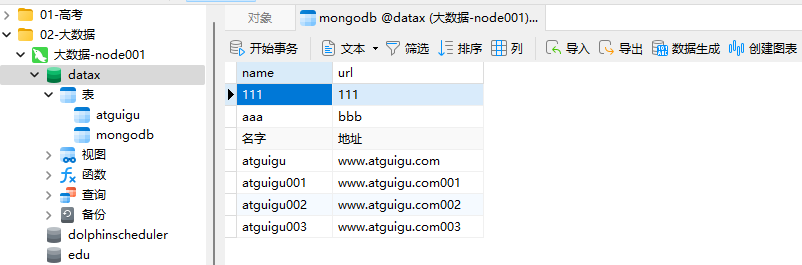
DataX,MongoDB数据导入hdfs与mysql
【尚硅谷】Alibaba开源数据同步工具DataX技术教程【尚硅谷】Alibaba开源数据同步工具DataX技术教程_哔哩哔哩_bilibili 目录 1、MongoDB 1.1、MongoDB介绍 1.2、MongoDB基本概念解析 1.3、MongoDB中的数据存储结构 1.4、MongoDB启动服务 1.5、MongoDB小案例 2、DataX导入…...
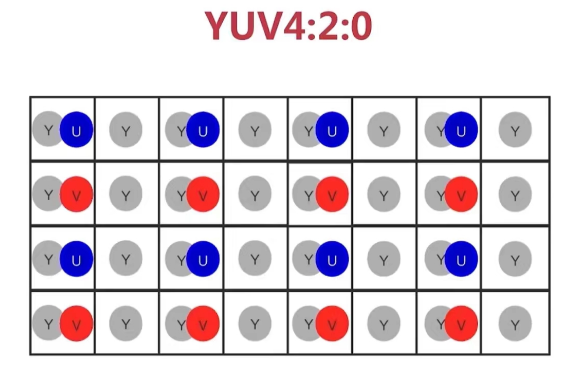
【OpenCV-颜色空间】
OpenCV-颜色空间 ■ RGB■ BGR■ HSV■ HSL■ HUE■ YUV ■ RGB ■ BGR BGR 就是RGB R和B调换位置。 OpenCV 默认使用BGR ■ HSV ■ HSL ■ HUE ■ YUV...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
