LeetCode 994—— 腐烂的橘子
阅读目录
- 1. 题目
- 2. 解题思路
- 3. 代码实现
1. 题目

2. 解题思路
- 1.记录下初始新鲜橘子的位置到
notRotting,我们按照行把二维数组拉成一维,所以,一个vector就可以实现了; - 2.如果没有新鲜橘子,那么第 0 分钟所有橘子已经腐烂,直接返回;
- 3.如果有新鲜橘子,那么我们遍历每一个新鲜橘子,查看它的上下左右是否有腐烂的橘子,如果有,代表这一分钟这个新鲜橘子会被腐烂,记录到
cur_Rotting,否则,这一分钟这个橘子仍然保持新鲜,记录到cur_notRotting; - 4.遍历完后,分钟数增加
1,然后,我们把这一分钟腐烂的橘子对应的位置置为2; - 5.如果这一分钟之后,没有腐烂的橘子总数没有变化,也就是没有橘子被腐蚀,那么跳出循环,因为余下的没有腐烂的橘子永远也不会腐烂了;
- 6.如果这一分钟有橘子被腐烂,那么,更新未被腐烂的橘子
cur_notRotting到notRotting,重复步骤 3-6; - 7.如果
notRotting为空,代表所有橘子都被腐烂,返回分钟数,否则,有橘子不会被腐烂,返回-1;
3. 代码实现
class Solution {
public:int orangesRotting(vector<vector<int>>& grid) {int row = grid.size();int col = grid[0].size();vector<int> notRotting;// 记录初始未腐烂的橘子位置for (int i = 0; i < row; ++i) {for (int j = 0; j < col; ++j) {if (grid[i][j] == 1) {notRotting.push_back(i * col + j);}}}if (notRotting.empty()) {return 0;}int minute = 0;while (!notRotting.empty()) {vector<int> cur_notRotting; // 这一分钟仍然没有腐烂的橘子vector<int> cur_Rotting; // 这一分钟腐烂的橘子for (int k = 0; k < notRotting.size(); ++k) {int i = notRotting[k] / col;int j = notRotting[k] % col;// 上下左右有腐烂的橘子,那么这个新鲜橘子会被腐烂if (i-1 >= 0 && grid[i-1][j] == 2) {cur_Rotting.push_back(notRotting[k]);continue;}if (i+1 < row && grid[i+1][j] == 2) {cur_Rotting.push_back(notRotting[k]);continue;}if (j-1 >= 0 && grid[i][j-1] == 2) {cur_Rotting.push_back(notRotting[k]);continue;}if (j+1 < col && grid[i][j+1] == 2) {cur_Rotting.push_back(notRotting[k]);continue;}// 否则,这个橘子继续保持新鲜cur_notRotting.push_back(notRotting[k]);}// 这一分钟腐烂的橘子更新状态for (int k = 0; k < cur_Rotting.size(); ++k) {int i = cur_Rotting[k] / col;int j = cur_Rotting[k] % col;grid[i][j] = 2;}minute += 1;// 这一分钟没有橘子被腐烂,跳出循环if (cur_notRotting.size() == notRotting.size()) {break;}// 更新未腐烂橘子的位置notRotting = cur_notRotting;}if (!notRotting.empty()) {return -1;} else {return minute;}}
};
时间复杂度为 O ( m n ) O(mn) O(mn),空间复杂度为 O ( m n ) O(mn) O(mn)。
相关文章:

LeetCode 994—— 腐烂的橘子
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 1.记录下初始新鲜橘子的位置到 notRotting,我们按照行把二维数组拉成一维,所以,一个vector 就可以实现了;2.如果没有新鲜橘子,那么第 0 分钟所有橘子已经…...

向上向下采样
在数字图像处理中,向上采样(upsampling)和向下采样(downsampling)是两种常见的操作,用于改变图像的分辨率。 向上采样(Upsampling): 向上采样是指增加图像的分辨率&…...

Leetcode面试经典150_Q169多数元素
题目: 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊n/2⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 解题思路: 1. 注意“大于 ⌊n/2⌋”,…...

Spring Cloud微服务入门(五)
Sentinel的安装与使用 安装部署Sentinel 下载Sentinel: https://github.com/alibaba/Sentinel/releases Sentinel控制台 https://localhost:8080 用户和密码为sentinel 使用Sentinel 加依赖: 写配置: 输入: java -Dserver.po…...

负荷预测 | Matlab基于TCN-GRU-Attention单输入单输出时间序列多步预测
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab基于TCN-GRU-Attention单输入单输出时间序列多步预测; 2.单变量时间序列数据集,采用前12个时刻预测未来96个时刻的数据; 3.excel数据方便替换,运行环境matlab20…...

SpringBoot整合Spring Data JPA
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉🍎个人主页:Leo的博客💞当前专栏: 循序渐进学SpringBoot ✨特色专栏: MySQL学习 🥭本文内容: SpringBoot整合Spring Data JPA 📚个人知识库: Leo知识库,欢迎大家访问 1.…...

机器学习(五) -- 监督学习(2) -- k近邻
系列文章目录及链接 目录 前言 一、K近邻通俗理解及定义 二、原理理解及公式 1、距离度量 四、接口实现 1、鸢尾花数据集介绍 2、API 3、流程 3.1、获取数据 3.2、数据预处理 3.3、特征工程 3.4、knn模型训练 3.5、模型评估 3.6、结果预测 4、超参数搜索-网格搜…...

【.NET全栈】ZedGraph图表库的介绍和应用
文章目录 一、ZedGraph介绍ZedGraph的特点ZedGraph的缺点使用注意事项 二、ZedGraph官网三、ZedGraph的应用四、ZedGraph的高端应用五、、总结 一、ZedGraph介绍 ZedGraph 是一个用于绘制图表和图形的开源.NET图表库。它提供了丰富的功能和灵活性,可以用于创建各种…...

vivado 设计调试
设计调试 对 FPGA 或 ACAP 设计进行调试是一个多步骤迭代式流程。与大多数复杂问题的处理方式一样 , 最好先将 FPGA 或 ACAP 设计调试流程细分为多个小部分 , 以便集中精力使设计中的每一小部分能逐一正常运行 , 而不是尝试一次性让整 个…...

Python3 replace()函数使用详解:字符串的艺术转换
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

【C++】用红黑树封装map和set
我们之前学的map和set在stl源码中都是用红黑树封装实现的,当然,我们也可以模拟来实现一下。在实现之前,我们也可以看一下stl源码是如何实现的。我们上篇博客写的红黑树里面只是一个pair对象,这对于set来说显然是不合适的ÿ…...

一些好玩的东西
这里写目录标题 递归1.递归打印数组和链表?代码实现原理讲解二叉树的 前 中 后 序位置 参考文章 递归 1.递归打印数组和链表? 平常我们打印数组和链表都是 迭代 就好了今天学到一个新思路–>不仅可以轻松正着打印数组和链表 , 还能轻松倒着打印(用的是二叉树的前中后序遍…...

微电网优化:基于巨型犰狳优化算法(Giant Armadillo Optimization,GAO)的微电网优化(提供MATLAB代码)
一、微电网优化模型 微电网是一个相对独立的本地化电力单元,用户现场的分布式发电可以支持用电需求。为此,您的微电网将接入、监控、预测和控制您本地的分布式能源系统,同时强化供电系统的弹性,保障您的用电更经济。您可以在连接…...

java锁
乐观锁 乐观锁是一种乐观思想,即认为读多写少,遇到并发写的可能性低,每次去拿数据的时候都认为别人不会修改,所以不会上锁,但是在更新的时候会判断一下在此期间别人有没有去更新这个数据,采取在写时先读出…...

QA测试开发工程师面试题满分问答6: 如何判断接口功能正常?从QA的角度设计测试用例
判断接口功能是否正常的方法之一是设计并执行相关的测试用例。下面是从测试QA的角度设计接口测试用例的一些建议,包括功能、边界、异常、链路、上下游和并发等方面: 通过综合考虑这些测试维度,并设计相应的测试用例,可以更全面地评估接口的功能、性能、安全性、数据一致…...

vue 双向绑定
双向绑定:双方其中一方改变,另外一方也会跟着改变。 data() { return {inputValue: ,list: [],message: hello,checked: true,radio: ,select: [],options: [{text: A, value:{value: A}},{text: B, value:{value: B}},{text: C, value:{value: C}}], }…...

python--异常处理
异常处理 例一: try: #可能出现异常代码 except: #如果程序异常,则立刻进入这儿 [finally: #不管是否捕获异常,finally语法快必须要执行!!! #资源关闭,等各种非常重要的操作&…...
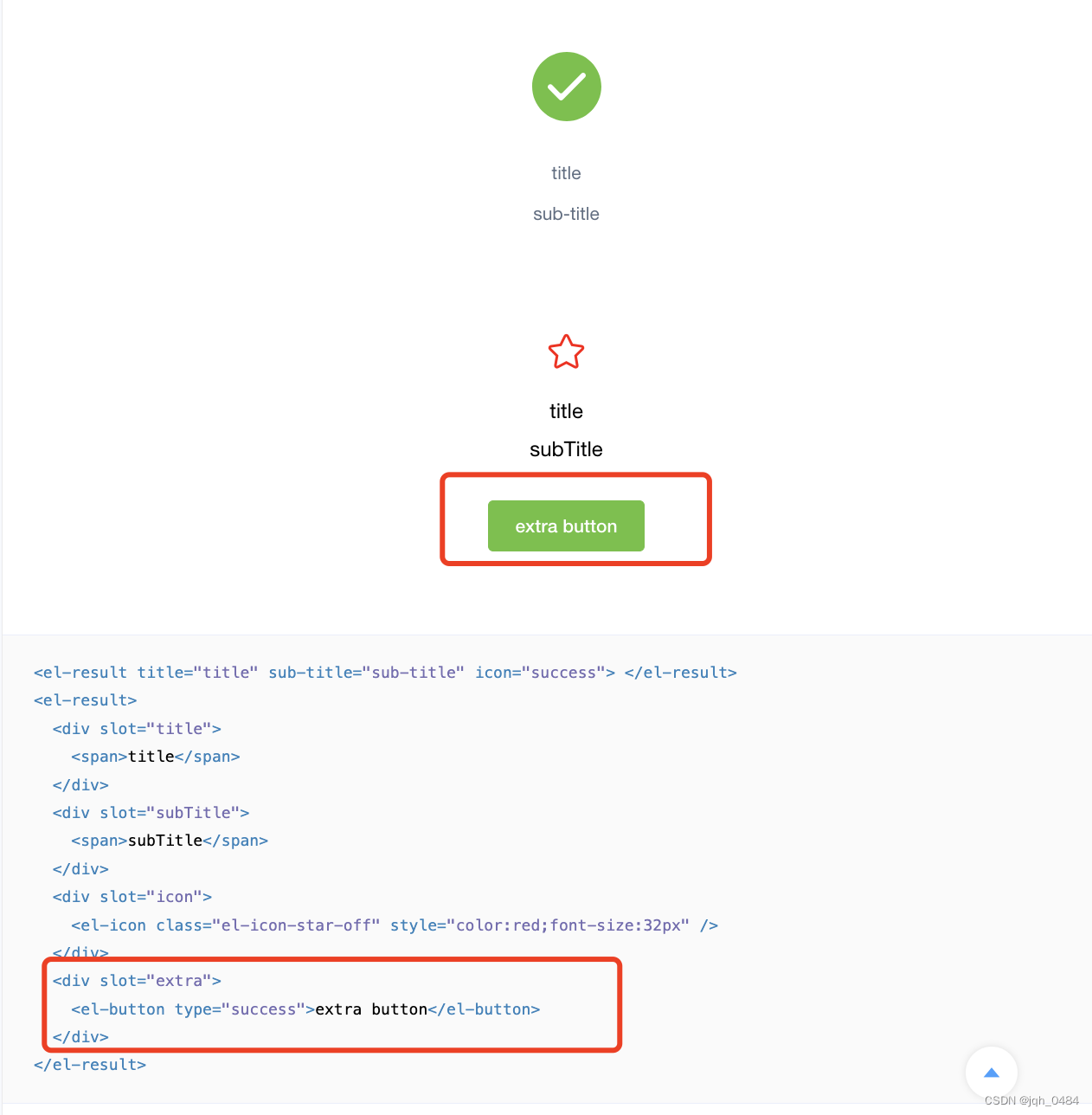
element-ui result 组件源码分享
今日简单分享 result 组件的源码实现,主要从以下三个方面: 1、result 组件页面结构 2、result 组件属性 3、result 组件 slot 一、result 组件页面结构 二、result 组件属性 2.1 title 属性,标题,类型 string,无默…...

VRRP虚拟路由实验(思科)
一,技术简介 VRRP(Virtual Router Redundancy Protocol)是一种网络协议,用于实现路由器冗余,提高网络可靠性和容错能力。VRRP允许多台路由器共享一个虚拟IP地址,其中一台路由器被选为Master,负…...
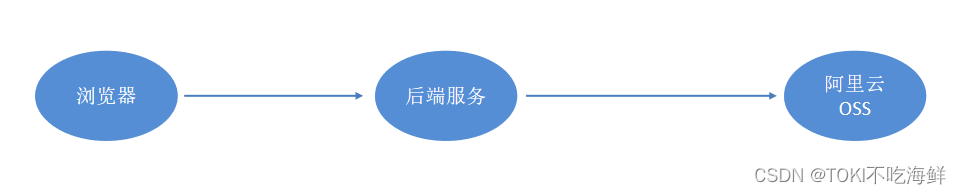
SpringBoot通用模块--文件上传开发(阿里云OSS)
文件上传,是指将本地图片、视频、音频等文件上传到服务器上,可以供其他用户浏览或下载的过程。文件上传在项目中应用非常广泛,我们经常发抖音、发朋友圈都用到了文件上传功能。 实现文件上传服务,需要有存储的支持,那…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
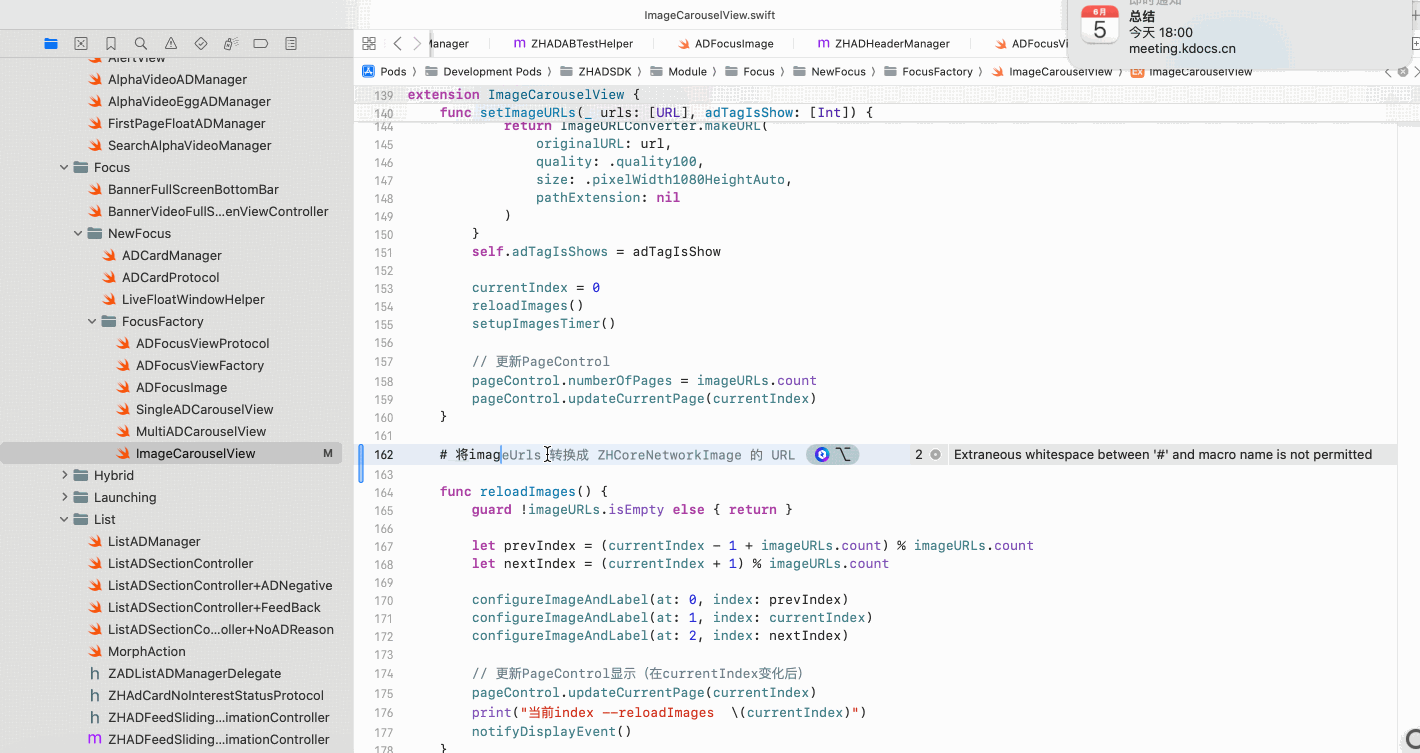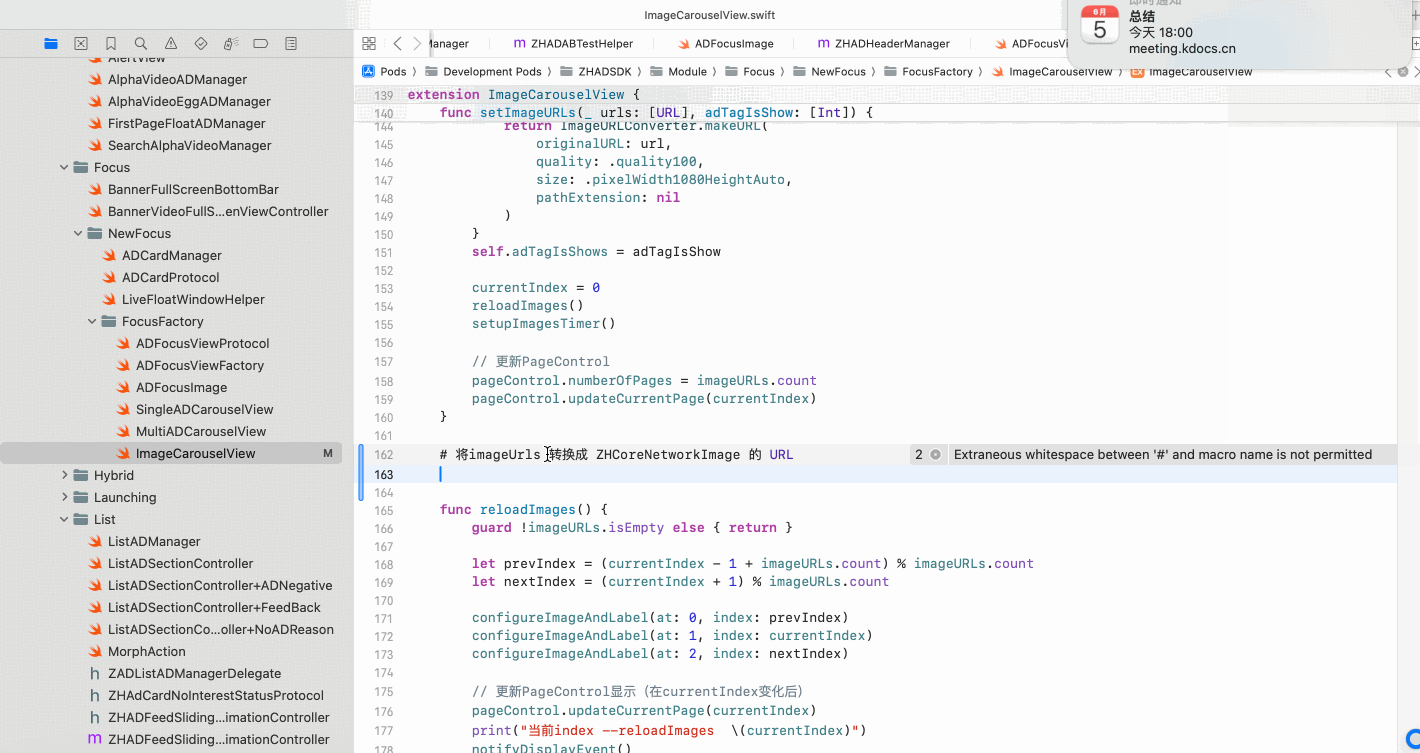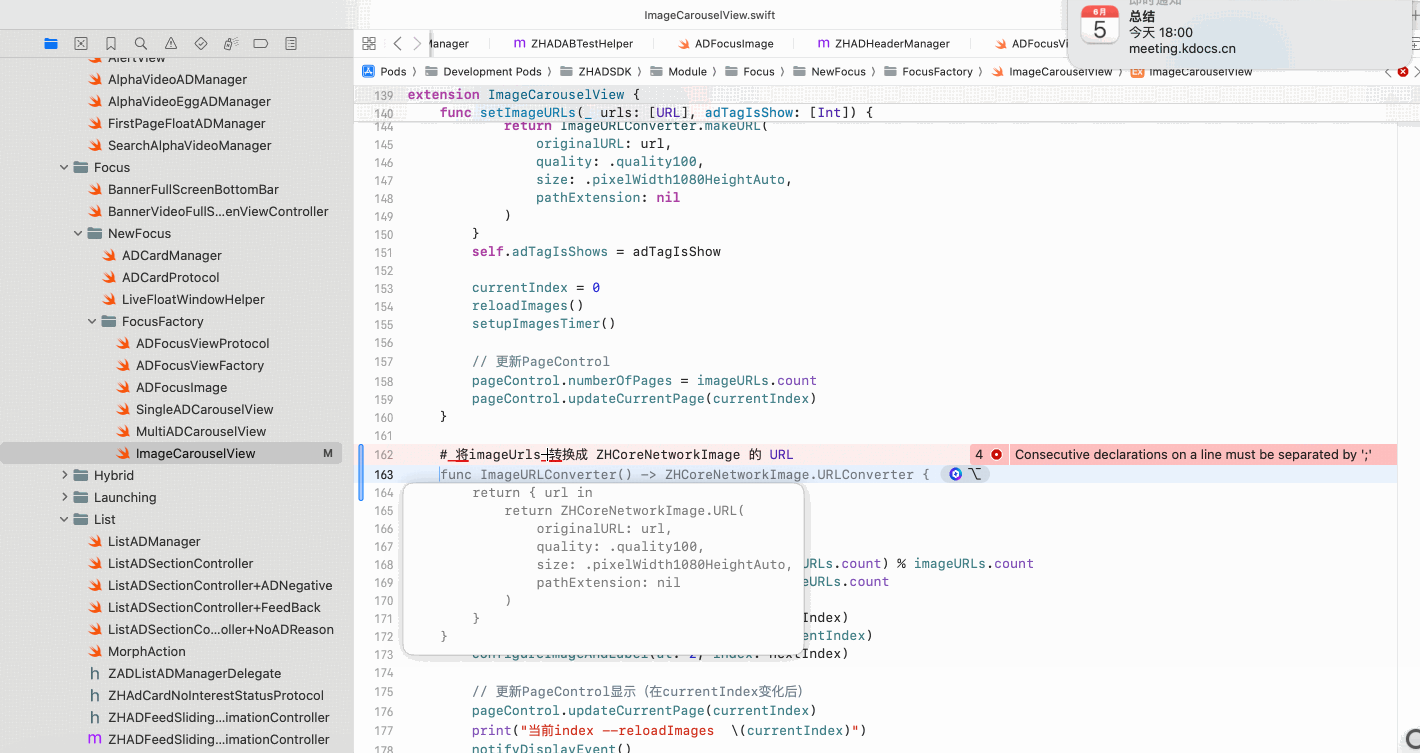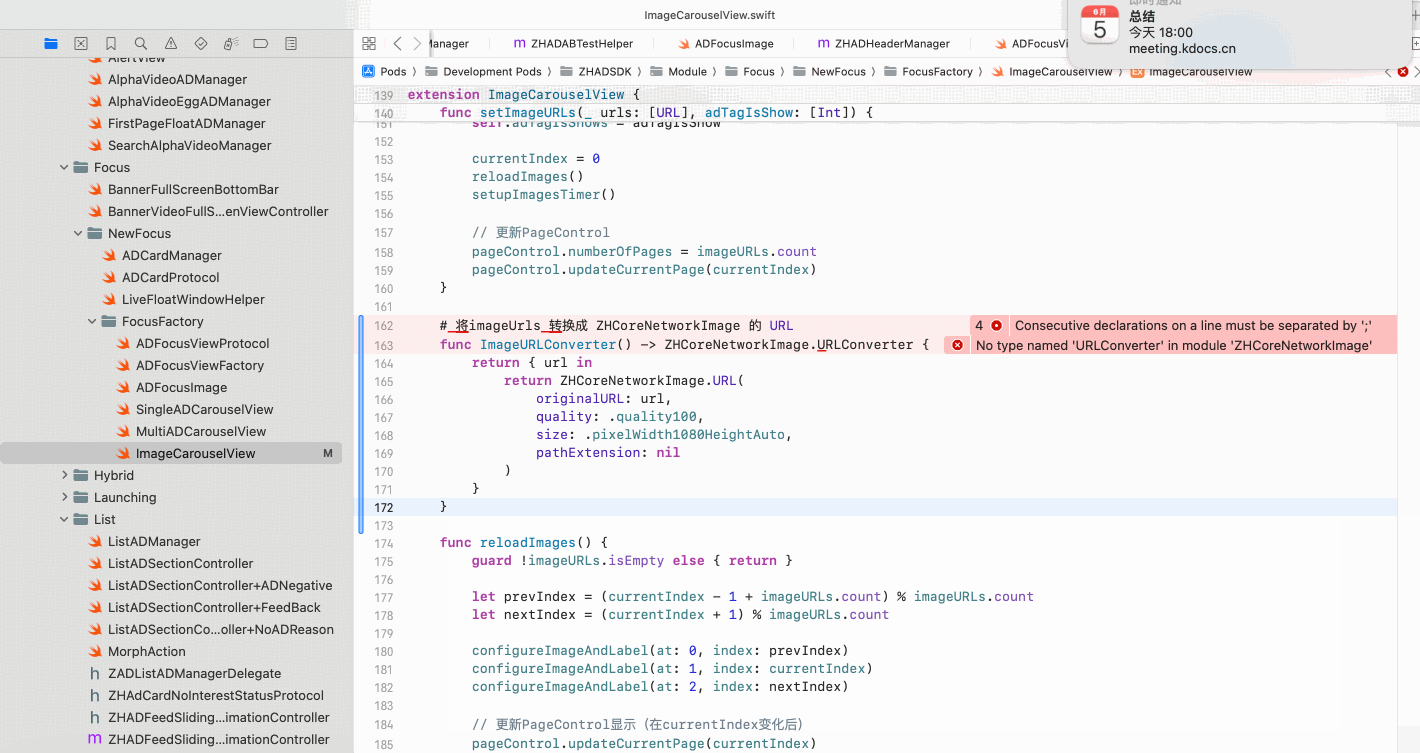
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

大模型智能体核心技术:CoT与ReAct深度解析
**导读:**在当今AI技术快速发展的背景下,大模型的推理能力和可解释性成为业界关注的焦点。本文深入解析了两项核心技术:CoT(思维链)和ReAct(推理与行动),这两种方法正在重新定义大模…...

2025 cs144 Lab Checkpoint 3: TCP Receiver
文章目录 1 关于TCP Sender1.1 关键机制重传超时(RTO)与定时器 2 实现TCP Sender2.1 void push( const TransmitFunction& transmit );const TransmitFunction& transmit 函数型参数?从哪里读取字节࿱…...
