每日OJ题_两个数组dp⑤_力扣10. 正则表达式匹配
目录
力扣10. 正则表达式匹配
解析代码
力扣10. 正则表达式匹配
10. 正则表达式匹配
难度 困难
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa", p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab", p = ".*" 输出:true 解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
提示:
1 <= s.length <= 201 <= p.length <= 20s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。- 保证每次出现字符
*时,前面都匹配到有效的字符
class Solution {
public:bool isMatch(string s, string p) {}
};解析代码
状态表示:
对于两个字符串之间的 dp 问题,一般的思考方式如下:
选取第⼀个字符串的 [0, i] 区间以及第⼆个字符串的 [0, j] 区间当成研究对象,结合题目的要求来定义状态表示。然后根据两个区间上最后一个位置的字符,来进行分类讨论,从而确定状态转移方程。
dp[i][j] 表示:字符串 p 的 [0, j] 区间和字符串 s 的 [0, i] 区间是否可以匹配。
状态转移方程:
根据最后一个位置的元素,结合题目要求,分情况讨论:
- 当 p[j] 不是特殊字符,且不与 s[i] 相等时,无法匹配。
- 当 s[i] == p[j] 或 p[j] == '.' 的时候,此时两个字符串匹配上了当前的一个字符, 只能从 dp[i - 1][j - 1] 中看当前字符前面的两个子串是否匹配。只能继承上个状态中的匹配结果, dp[i][j] = dp[i - 1][j - 1] ;
- b. 当 p[j] == '*' 的时候,和力扣44. 通配符匹配稍有不同的是,上道题 "*" 本身便可匹配 0 ~ n 个字符,但此题是要带着 p[j - 1] 的字符⼀起,匹配 0 ~ n 个和 p[j - 1] 相同的字符。此时,匹配策略有两种选择:
- 一种选择是: p[j - 1]* 匹配空字符串,直接继承状态 dp[i][j - 2] ,此时 dp[i][j] = dp[i][j - 2] ;
- 另一种选择是: p[j - 1]* 向前匹配 1 ~ n 个字符(与力扣44. 通配符匹配不同,此时p[j - 1]与s[i] 要相等 或者 p[j - 1] 为点),直至匹配上整个 s 串。此时相当于从 dp[k][j - 2] (0 < k <= i) 中所有匹配情况中,选择性继承可以成功的情况。此时 dp[i][j] = dp[k][j - 2] (0 < k <= i 且 s[k]~s[i] = p[j - 1]) ;
三种情况加起来,就是所有可能的匹配结果。 综上所述,状态转移方程为:
- 当s[i] == p[j] 或 p[j] == '.' 时: dp[i][j] = dp[i][j - 1] ;
- 当 p[j] == '*' 时,有多种情况需要讨论: dp[i][j] = dp[i][j - 2] ; dp[i][j] = dp[k][j - 1] (0 <= k <= i) ;
这个状态转移方程时间复杂度为O(N^3),要想想优化。
优化:当发现计算一个状态的时候,需要一个循环才能搞定的时候,我们要想到去优化。优化的方向就是用一个或者两个状态来表示这一堆的状态。通常就是把它写下来,然后用数学的方式做一下等价替换:
当 p[j] == '*' 时,状态转移方程为:dp[i][j] = dp[i][j - 2] || dp[i - 1][j - 2] || dp[i - 2][j - 2] ......
发现 i 是有规律的减小的,因此我们去看看 dp[i - 1][j] ,列出 dp[i - 1][j] = dp[i - 1][j - 1] || dp[i - 2][j - 1] || dp[i - 3][j - 1] ......
然后就能发现, dp[i][j] 的状态转移方程里面除了第一项以外,其余的都可以用dp[i -1][j] 替代。因此优化我们的状态转移方程为: dp[i][j] = dp[i][j - 2] || dp[i - 1][j]。
初始化、填表顺序、返回值:
初始化:空串是有研究意义的,因此我们将原始 dp 表的规模多加上一行和一列,表示空串。由于 dp 数组的值设置为是否匹配,为了不与答案值混淆,我们需要将整个数组初始化为false 。由于需要用到前一行和前一列的状态,初始化第一行、第一列即可。
dp[0][0] 表示两个空串能否匹配,答案是显然的, 初始化为 true 。
第一行表示 s 是一个空串, p 串和空串只有一种匹配可能,即 p 串表示为 "任一字符+*" ,此时也相当于空串匹配上空串。所以可以遍历 p 串,把所有前导为 "任一字符+*" 的 p 子串和空串的 dp 值设为 true 。
第一列表示 p 是一个空串,不可能匹配上 s 串,跟随数组初始化成false即可。
填表顺序:从上往下填写每一行,每一行从左往右,最后返回dp[m][n]。
class Solution {
public:bool isMatch(string s, string p) {// dp[i][j]表示字符串p的[0, j]区间和字符串s的[0, i]区间是否可以匹配int m = s.size(), n = p.size();s = " " + s, p = " " + p;vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false));dp[0][0] = true;for(int j = 2; j <= n; j += 2){if(p[j] == '*')dp[0][j] = true;elsebreak;}for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){if(s[i] == p[j] || p[j] == '.'){dp[i][j] = dp[i - 1][j - 1];}else if(p[j] == '*'){ // j-1为点 或者 和s[i]相等才可以匹配dp[i - 1][j]if(p[j - 1] == '.' || p[j - 1] == s[i])dp[i][j] = dp[i][j - 2] || dp[i - 1][j];else // 匹配空串的dp[i][j] = dp[i][j - 2];}}}return dp[m][n];}
};
相关文章:

每日OJ题_两个数组dp⑤_力扣10. 正则表达式匹配
目录 力扣10. 正则表达式匹配 解析代码 力扣10. 正则表达式匹配 10. 正则表达式匹配 难度 困难 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 . 和 * 的正则表达式匹配。 . 匹配任意单个字符* 匹配零个或多个前面的那一个元素 所谓匹配,…...
开源区块链系统/技术 总结(欢迎补充,最新)
一、联盟链 1. FISCO BCOS FISCO BCOS 2.0 技术文档 — FISCO BCOS 2.0 v2.9.0 文档https://fisco-bcos-documentation.readthedocs.io/ 2. ChainMaker(长安链) 文档导航 — chainmaker-docs v2.3.2 documentationhttps://docs.chainmaker.org.cn/v2…...

LeetCode 994—— 腐烂的橘子
阅读目录 1. 题目2. 解题思路3. 代码实现 1. 题目 2. 解题思路 1.记录下初始新鲜橘子的位置到 notRotting,我们按照行把二维数组拉成一维,所以,一个vector 就可以实现了;2.如果没有新鲜橘子,那么第 0 分钟所有橘子已经…...

向上向下采样
在数字图像处理中,向上采样(upsampling)和向下采样(downsampling)是两种常见的操作,用于改变图像的分辨率。 向上采样(Upsampling): 向上采样是指增加图像的分辨率&…...

Leetcode面试经典150_Q169多数元素
题目: 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊n/2⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 解题思路: 1. 注意“大于 ⌊n/2⌋”,…...

Spring Cloud微服务入门(五)
Sentinel的安装与使用 安装部署Sentinel 下载Sentinel: https://github.com/alibaba/Sentinel/releases Sentinel控制台 https://localhost:8080 用户和密码为sentinel 使用Sentinel 加依赖: 写配置: 输入: java -Dserver.po…...

负荷预测 | Matlab基于TCN-GRU-Attention单输入单输出时间序列多步预测
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab基于TCN-GRU-Attention单输入单输出时间序列多步预测; 2.单变量时间序列数据集,采用前12个时刻预测未来96个时刻的数据; 3.excel数据方便替换,运行环境matlab20…...

SpringBoot整合Spring Data JPA
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉🍎个人主页:Leo的博客💞当前专栏: 循序渐进学SpringBoot ✨特色专栏: MySQL学习 🥭本文内容: SpringBoot整合Spring Data JPA 📚个人知识库: Leo知识库,欢迎大家访问 1.…...

机器学习(五) -- 监督学习(2) -- k近邻
系列文章目录及链接 目录 前言 一、K近邻通俗理解及定义 二、原理理解及公式 1、距离度量 四、接口实现 1、鸢尾花数据集介绍 2、API 3、流程 3.1、获取数据 3.2、数据预处理 3.3、特征工程 3.4、knn模型训练 3.5、模型评估 3.6、结果预测 4、超参数搜索-网格搜…...

【.NET全栈】ZedGraph图表库的介绍和应用
文章目录 一、ZedGraph介绍ZedGraph的特点ZedGraph的缺点使用注意事项 二、ZedGraph官网三、ZedGraph的应用四、ZedGraph的高端应用五、、总结 一、ZedGraph介绍 ZedGraph 是一个用于绘制图表和图形的开源.NET图表库。它提供了丰富的功能和灵活性,可以用于创建各种…...

vivado 设计调试
设计调试 对 FPGA 或 ACAP 设计进行调试是一个多步骤迭代式流程。与大多数复杂问题的处理方式一样 , 最好先将 FPGA 或 ACAP 设计调试流程细分为多个小部分 , 以便集中精力使设计中的每一小部分能逐一正常运行 , 而不是尝试一次性让整 个…...

Python3 replace()函数使用详解:字符串的艺术转换
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

【C++】用红黑树封装map和set
我们之前学的map和set在stl源码中都是用红黑树封装实现的,当然,我们也可以模拟来实现一下。在实现之前,我们也可以看一下stl源码是如何实现的。我们上篇博客写的红黑树里面只是一个pair对象,这对于set来说显然是不合适的ÿ…...

一些好玩的东西
这里写目录标题 递归1.递归打印数组和链表?代码实现原理讲解二叉树的 前 中 后 序位置 参考文章 递归 1.递归打印数组和链表? 平常我们打印数组和链表都是 迭代 就好了今天学到一个新思路–>不仅可以轻松正着打印数组和链表 , 还能轻松倒着打印(用的是二叉树的前中后序遍…...

微电网优化:基于巨型犰狳优化算法(Giant Armadillo Optimization,GAO)的微电网优化(提供MATLAB代码)
一、微电网优化模型 微电网是一个相对独立的本地化电力单元,用户现场的分布式发电可以支持用电需求。为此,您的微电网将接入、监控、预测和控制您本地的分布式能源系统,同时强化供电系统的弹性,保障您的用电更经济。您可以在连接…...

java锁
乐观锁 乐观锁是一种乐观思想,即认为读多写少,遇到并发写的可能性低,每次去拿数据的时候都认为别人不会修改,所以不会上锁,但是在更新的时候会判断一下在此期间别人有没有去更新这个数据,采取在写时先读出…...

QA测试开发工程师面试题满分问答6: 如何判断接口功能正常?从QA的角度设计测试用例
判断接口功能是否正常的方法之一是设计并执行相关的测试用例。下面是从测试QA的角度设计接口测试用例的一些建议,包括功能、边界、异常、链路、上下游和并发等方面: 通过综合考虑这些测试维度,并设计相应的测试用例,可以更全面地评估接口的功能、性能、安全性、数据一致…...

vue 双向绑定
双向绑定:双方其中一方改变,另外一方也会跟着改变。 data() { return {inputValue: ,list: [],message: hello,checked: true,radio: ,select: [],options: [{text: A, value:{value: A}},{text: B, value:{value: B}},{text: C, value:{value: C}}], }…...

python--异常处理
异常处理 例一: try: #可能出现异常代码 except: #如果程序异常,则立刻进入这儿 [finally: #不管是否捕获异常,finally语法快必须要执行!!! #资源关闭,等各种非常重要的操作&…...
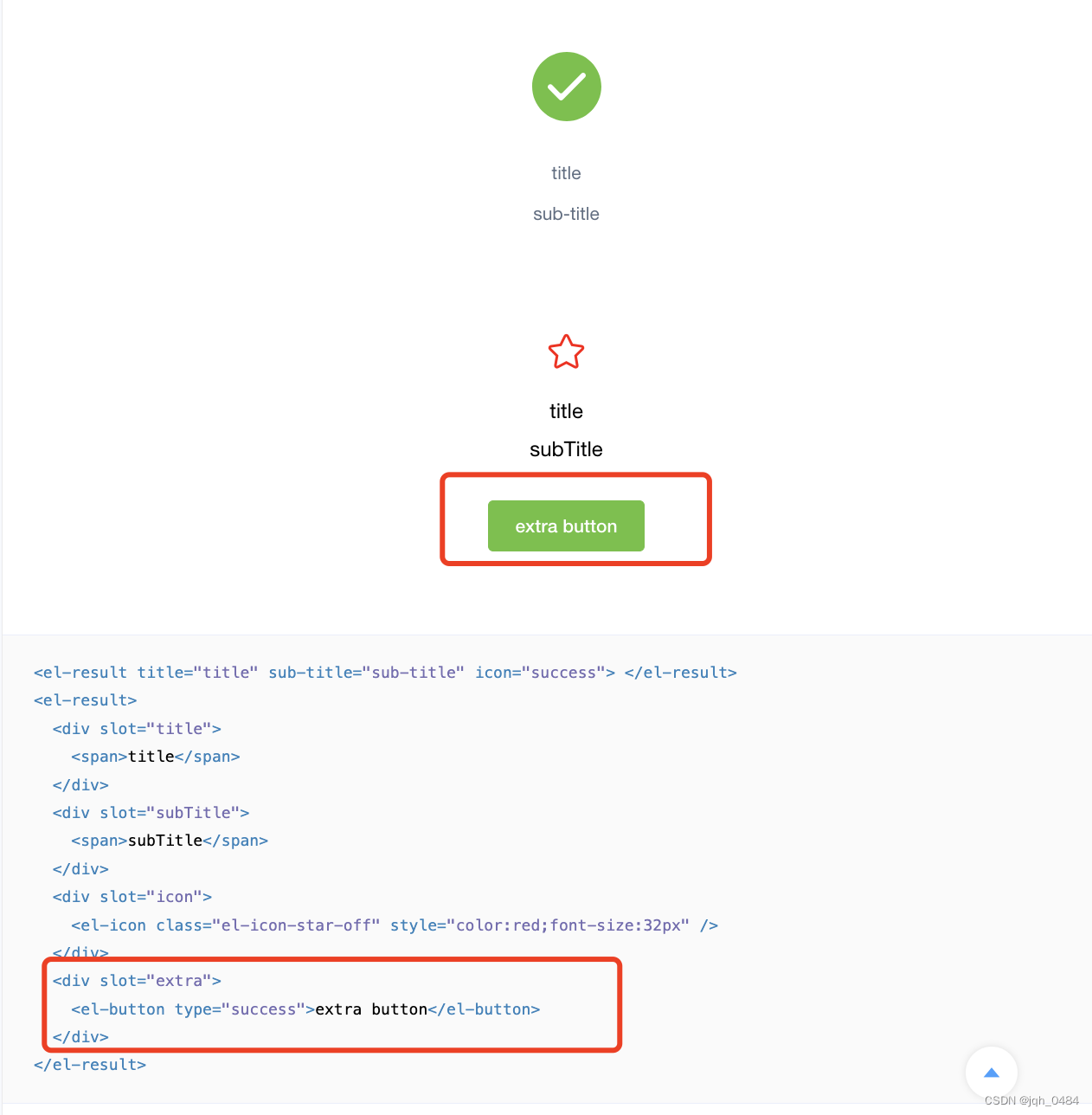
element-ui result 组件源码分享
今日简单分享 result 组件的源码实现,主要从以下三个方面: 1、result 组件页面结构 2、result 组件属性 3、result 组件 slot 一、result 组件页面结构 二、result 组件属性 2.1 title 属性,标题,类型 string,无默…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
