leetcode刷题-代码训练营-第7章-回溯算法1
回溯法模板
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
理解
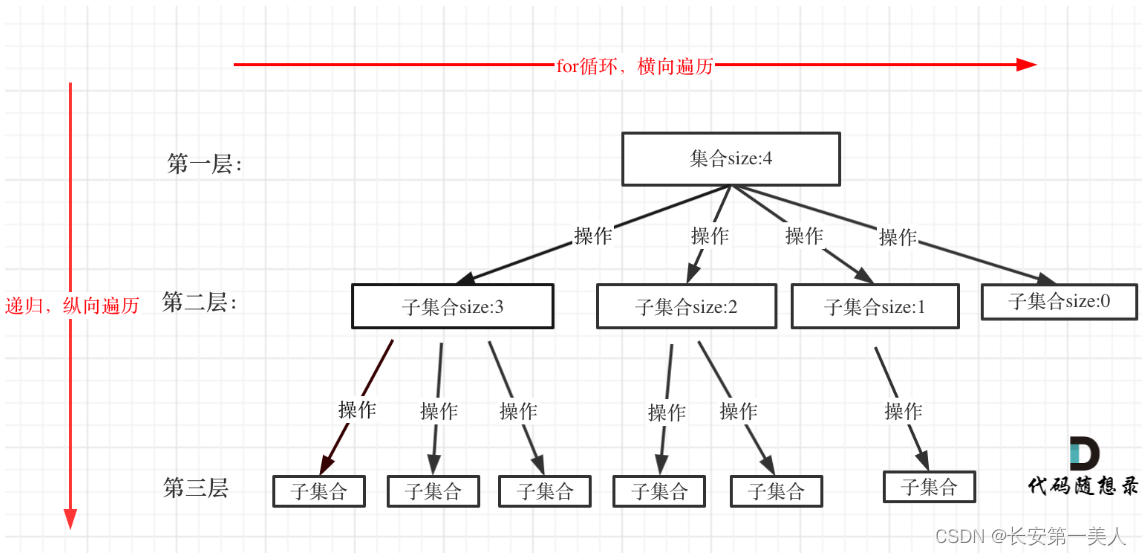
从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了
回溯法解决的问题都可以抽象为树形结构(N叉树),用树形结构来理解回溯就容易多了
第77题. 组合

理解

回溯代码
class Solution {
private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点 backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {result.clear(); // 可以不写path.clear(); // 可以不写backtracking(n, k, 1);return result;}
};
剪枝操作
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方path.push_back(i); // 处理节点backtracking(n, k, i + 1);path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};216.组合总和III

思路

回溯算法
class Solution {
private:vector<vector<int>> result; // 存放结果集vector<int> path; // 符合条件的结果// targetSum:目标和,也就是题目中的n。// k:题目中要求k个数的集合。// sum:已经收集的元素的总和,也就是path里元素的总和。// startIndex:下一层for循环搜索的起始位置。void backtracking(int targetSum, int k, int sum, int startIndex) {if (path.size() == k) {if (sum == targetSum) result.push_back(path);return; // 如果path.size() == k 但sum != targetSum 直接返回}for (int i = startIndex; i <= 9; i++) {sum += i; // 处理path.push_back(i); // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯}}public:vector<vector<int>> combinationSum3(int k, int n) {result.clear(); // 可以不加path.clear(); // 可以不加backtracking(n, k, 0, 1);return result;}
};剪枝操作
class Solution {
private:vector<vector<int>> result; // 存放结果集vector<int> path; // 符合条件的结果void backtracking(int targetSum, int k, int sum, int startIndex) {if (sum > targetSum) { // 剪枝操作return; // 如果path.size() == k 但sum != targetSum 直接返回}if (path.size() == k) {if (sum == targetSum) result.push_back(path);return;}for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝sum += i; // 处理path.push_back(i); // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯}}public:vector<vector<int>> combinationSum3(int k, int n) {result.clear(); // 可以不加path.clear(); // 可以不加backtracking(n, k, 0, 1);return result;}
};17.电话号码的字母组合

39. 组合总和

思路
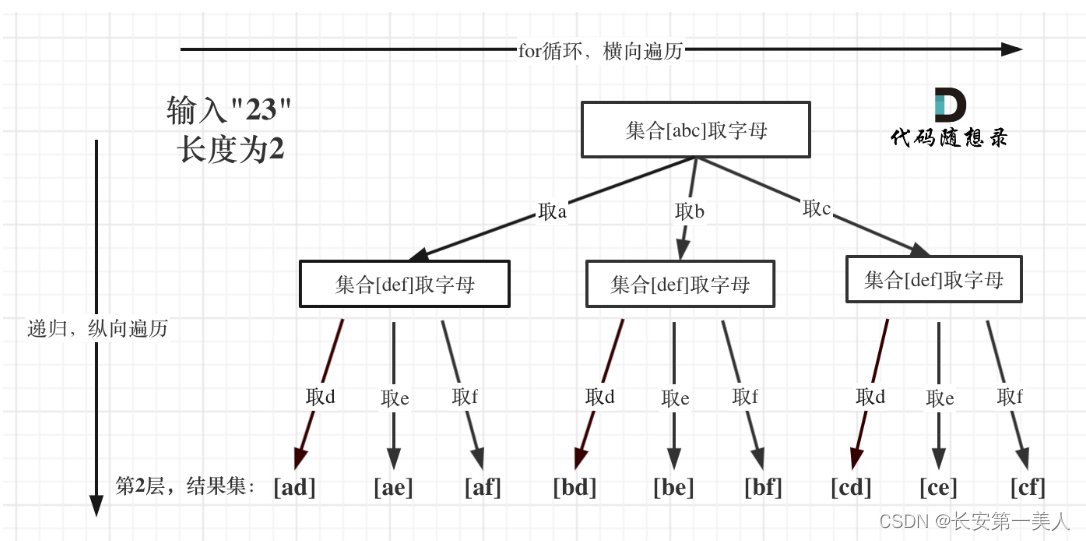
回溯法代码
// 版本一
class Solution {
private:const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};
public:vector<string> result;string s;void backtracking(const string& digits, int index) {if (index == digits.size()) {result.push_back(s);return;}int digit = digits[index] - '0'; // 将index指向的数字转为intstring letters = letterMap[digit]; // 取数字对应的字符集for (int i = 0; i < letters.size(); i++) {s.push_back(letters[i]); // 处理backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了s.pop_back(); // 回溯}}vector<string> letterCombinations(string digits) {s.clear();result.clear();if (digits.size() == 0) {return result;}backtracking(digits, 0);return result;}
};思路
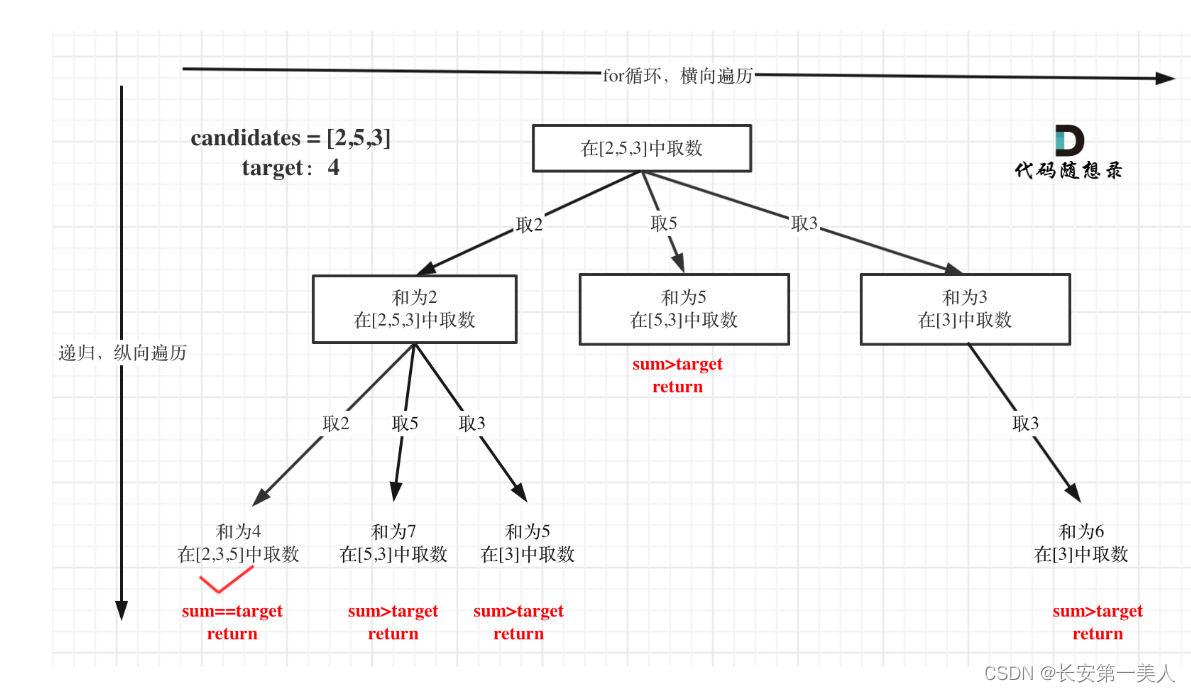
回溯算法
// 版本一
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum > target) {return;}if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();backtracking(candidates, target, 0, 0);return result;}
};优化代码
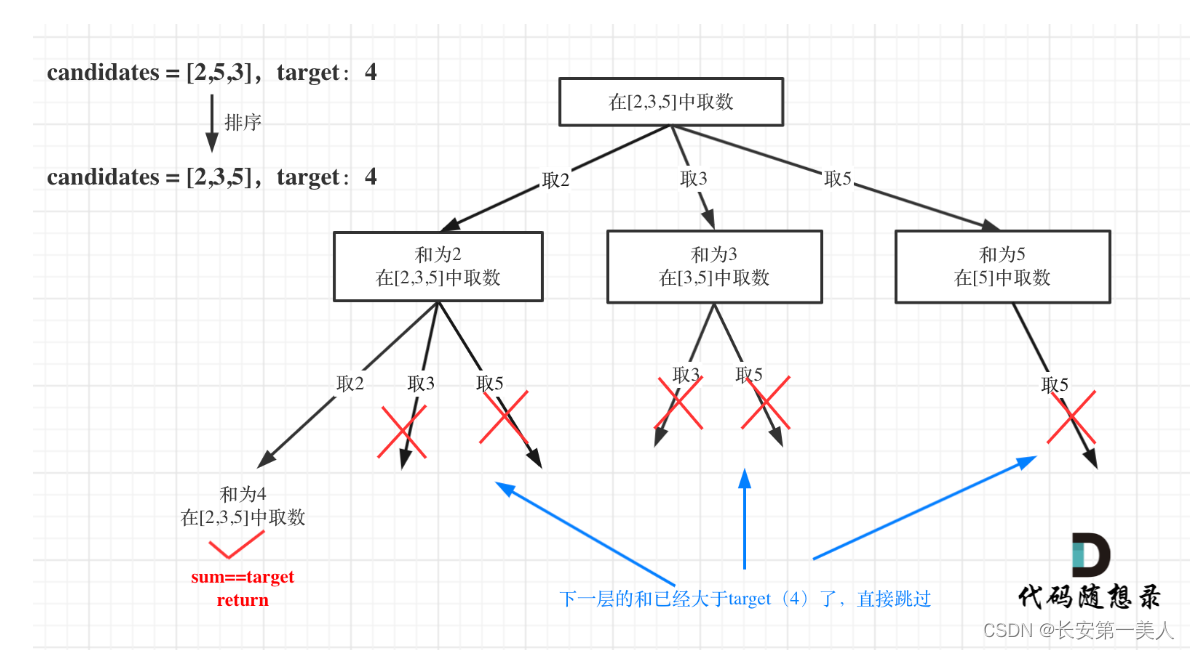
对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
在求和问题中,排序之后加剪枝是常见的套路!
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum == target) {result.push_back(path);return;}// 如果 sum + candidates[i] > target 就终止遍历for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i);sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();sort(candidates.begin(), candidates.end()); // 需要排序backtracking(candidates, target, 0, 0);return result;}
};相关文章:

leetcode刷题-代码训练营-第7章-回溯算法1
回溯法模板 void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果} }理解 从…...

三种常见webshell工具的流量特征分析
又来跟师傅们分享小技巧了,这次简单介绍一下三种常见的webshell流量分析,希望能对参加HW蓝队的师傅们有所帮助。 什么是webshell webshell就是以asp、php、jsp或者cgi等网页文件形式存在的一种代码执行环境,主要用于网站管理、服务器管理、…...

pkg打包nodejs程序用动态require路由出现问题
动态路由问题 pkg打包的时候会自动生成一个虚拟路径/snapshot/…会导致你的路径出现一些问题 而项目中依据route文件夹下的文件动态use相应的router,这就需要动态require,但是这个require的路径会被虚拟路径代替导致取不到,所以可以使用写死…...
行为型之策略模式)
设计模式(018)行为型之策略模式
策略模式是一种行为设计模式,它定义了一系列算法,将每个算法封装成一个对象,并使它们可以互换。策略模式使得算法的变化可以独立于使用算法的客户端。在策略模式中,有三个核心角色:策略接口(Strategy&#…...

c++关键字: =delete和=default
delete 概述 delete关键字是c11新增的关键字,主要用于的场景是:当我们不希望类中的函数被类对象在外部调用的时候,我们就可以使用这个关键字。 其实,之前我们实现这种功能是将这些函数放在private修饰符下,但是这种方…...

JSON
文章目录 JSONJSON 的定义格式快速入门JSON 对象和字符串对象转换JSON 在 java 中使用JSON与java对象的转换JSON与List集合的转换JSON与Map的转换 JSON JSON 指的是 JavaScript 对象表示法(JavaScript Object Notation) JSON 是轻量级的文本数据交换格式…...
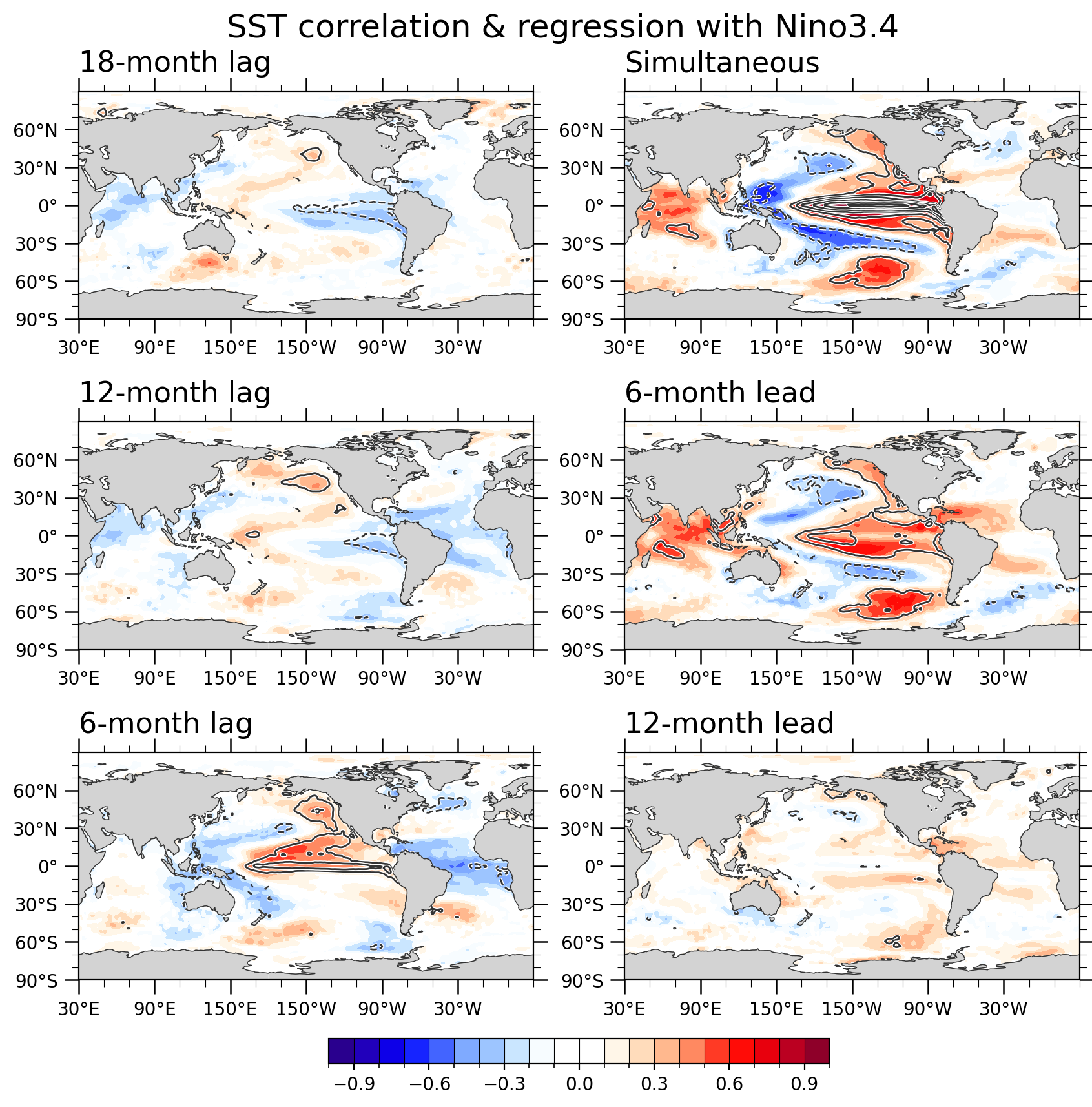
Python | 超前滞后分析
Nino SST Indices (Nino 12, 3, 3.4, 4; ONI and TNI) 有几个指标用于监测热带太平洋,所有这些指标都是基于海表温度(SST)异常在一个给定的区域的平均值。通常,异常是相对于30年的周期来计算的。厄尔尼诺3.4指数(Nio 3.4 index)和海洋厄尔尼诺指数(Ocea…...

Linux CPU利用率
Linux CPU利用率 在线上服务器观察线上服务运行状态的时候,绝大多数人都是喜欢先用 top 命令看看当前系统的整体 cpu 利用率。例如,随手拿来的一台机器,top 命令显示的利用率信息如下 这个输出结果说简单也简单,说复杂也不是那么…...

vue3实现导出pdf、png功能
准备做的系统中出现了 想导出当前页面的png或者pdf设计数据较多后端做可能比较麻烦 就自己研究了一下 1、安装html2canvas 、jspdf包 npm install --save html2canvas // 可以将dom元素转为一张图片 npm install --save jspdf // 导出为PDF格式 2、vue组件中引用&#x…...

what is tty?
waht is tty? 黑话:TTY 为什么使用Linux的时候CtrlC就会终止一个命令运行,ta是如何设置的? stty -a 桌面切换 CTRL ALT F1 – 锁屏 CTRL ALT F2 – 桌面环境 CTRL ALT F3 – TTY3 CTRL ALT F4 – TTY4 CTRL ALT F5 – TTY5 CTRL ALT F6 – TTY6...

在vite中限制node版本
1.修改package.json文件 {"name": "wine-store-frontend","version": "0.0.0","private": true,"type": "module","scripts": {"dev": "vite --open","build"…...

07 Php学习:运算符
PHP 算术运算符 在 PHP 中,算术运算符用于执行基本的数学运算,包括加法、减法、乘法、除法、取余数,负数运算、取反和并置运算。以下是这些运算符的详细解释和示例: 加法运算符 :用于将两个数值相加。 $a 5; $b 3;…...

做了多年前端,有没有想在python,go,nodejs,.net,java,c++中学一门后端,推荐
作为一名经验丰富的前端开发者,选择学习后端技术是一个重要的职业发展决策。Python、Go、Node.js、.NET、Java和C都是强大的后端开发语言,每门语言都有其特定的优势和应用场景。以下是对这些技术的分析,以帮助你做出选择: 目录 …...

JR-SMD201-P便携式网络解码器
详细介绍: JR-SMD201-P便携式网络解码器采用1/2U设计,支持AVS/H.265/H.264/MPEG2解码,支持IP输入,支持1080P/1080I/720P/576I/480I多种分辨率,支持DRA/AC3/EAC3/AAC/MPEG等音频。 产品特点 支持输入方式IP 接口丰富&a…...

线程池阻塞队列的选择
一、背景 想起前两年被问到阻塞队列怎么选,有界是必然的, ArrayBlockingQueue、LinkedBlockingQueue怎么选呢。 二、打开源码看看 ArrayBlockingQueue arrayBlockingQueue new ArrayBlockingQueue(3);LinkedBlockingQueue linkedBlockingQueue new Lin…...
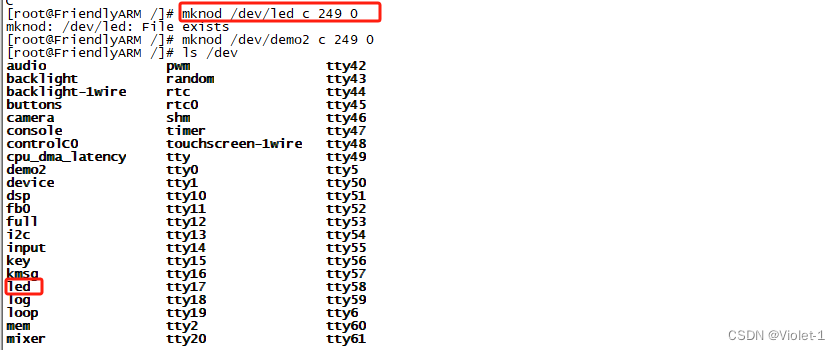
linux内核驱动-在内核代码里添加设备结点
linux中,一切皆文件 我们在用户层用一些系统函数(如:fopen等等)时,会进入内核,内核会在字符注册了的设备号链表中查找。如果找到就运行我们写的设备文件的(驱动)函数 我们在前面已经…...

【算法优选】 动态规划之简单多状态dp问题——贰
文章目录 🎋前言🌴[买卖股票的最佳时机含冷冻期](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/description/)🚩题目描述🚩算法思路:🎈状态表示:🎈…...

【算法刷题 | 二叉树 06】4.10( 路径总和、路径总和 || )
文章目录 13.路径总和13.1问题13.2解法一:递归13.2.1递归思路(1)确定递归函数参数以及返回值(2)确定终止条件(3)确定递归逻辑 13.2.2代码实现 14.路径总和 ||14.1问题14.2解法一:递归…...
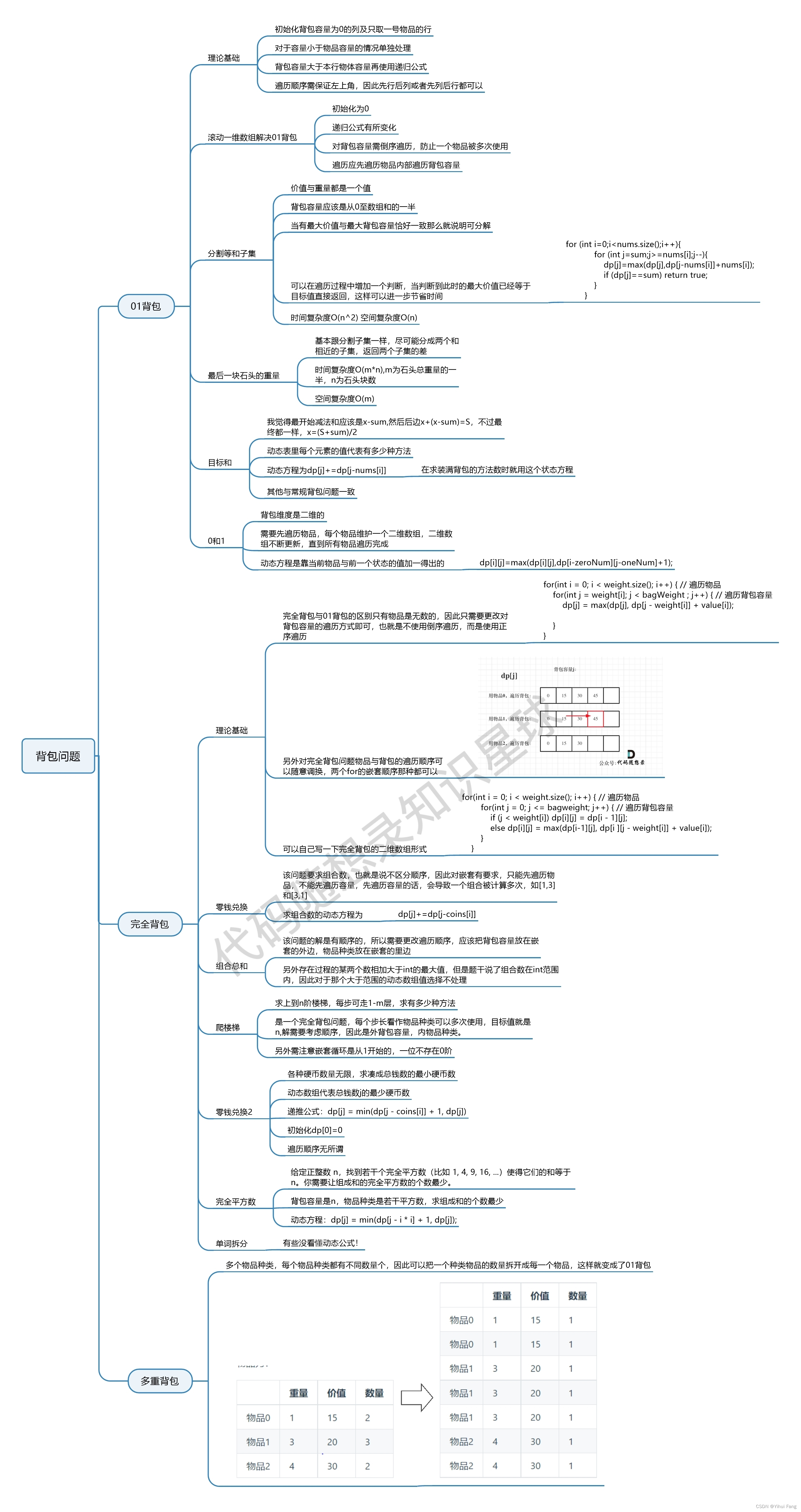
代码学习记录37----动态规划
随想录日记part37 t i m e : time: time: 2024.04.06 主要内容:今天开始要学习动态规划的相关知识了,今天的内容主要涉及四个方面: 完全背包;零钱兑换 II ;组合总和 Ⅳ 和单词拆分 …...

Spring Boot:Web开发之三大组件的整合
Spring Boot 前言Spring Boot 整合 ServletSpring Boot 整合 FilterSpring Boot 整合 Listener前言 在 Web 开发中,Servlet 、Filter 和 Listener 是 Java Web 应用中的三大组件。Servlet 是 Java 代码,通过 Java 的 API 动态的向客户端输出内容。Filter 是处于客户端与服务…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

