Linux——fork复制进程
1)shell:
在计算机科学中,Shell俗称壳(用来区别于核),是指“为使用者提供操作界面”的软件(command interpreter,命令解析器)。它类似于DOS下的COMMAND.COM和后来的cmd.exe。它接收用户命令,然后调用相应的应用程序。

我们就是通过命令解释器(称为shell)(bash是命令解释器中的一种)和内核和系统进行交互的(Windows通过图形界面进行交互的);例如我们把ls交给bash,bash帮我们运行ls,然后把结果给用户;

2)fork如何复制进程?
fork是把已有的进程复制一份,当然把PCB也复制了一份,然后申请一个PID,子进程的PID=父进程的PID+1;
 如果父子进程想要做不同的事情,那么我们通过返回值来判断; man fork
如果父子进程想要做不同的事情,那么我们通过返回值来判断; man fork
代码如下(代码下去自己练习,理解):
#include <stdio.h>
#include <unistd.h>
#include <assert.h>
#include <stdlib.h>int main()
{char *s=NULL;int n=0;//控制父子进程执行的次数;pid_t id=fork();assert(id!=-1);if(id==0)//子进程{s="child";n=3;}else//父进程{s="parent";n=7;}//父子进程int i=0;for(;i<n;i++){printf("s=%s\n",s);sleep(1);}exit(0);
}父子进程是两个独立的进程,各自执行各自的代码;如果父子进程要做不一样的事情,就通过if else返回值来操作;
3)fork的时机
fork产生的这个子进程不是从头开始执行的,而是从fork之后开始执行的,就是说fork下面的代码子进程才开始执行,具体的是说从返回值这里子进程开始执行,子进程不会再fork了,所以不会出现子进程再去fork产生一个子进程的问题. 也就是说:从返回值这里开始,父进程返回子进程的PID,子进程返回0;
4)getppid与getpid
getppid:得到一个进程的父进程的PID; getpid:得到当前进程的PID;
man getpid; man getppid
fork补充

相关文章:

Linux——fork复制进程
1)shell: 在计算机科学中,Shell俗称壳(用来区别于核),是指“为使用者提供操作界面”的软件(command interpreter,命令解析器)。它类似于DOS下的COMMAND.COM和后来的cmd.exe。它接收用户命令&…...
李廉洋:4.10黄金原油晚间走势最新分析及策略。
鉴于美联储官员对1月和2月通胀数据反应不足,3月通胀数据过热可能导致其反应过度的风险更大。美联储试图避免根据一两个数据点来制定政策,但今年迄今为止经济活动的韧性意味着,在年中降息的理由取决于通胀是否恢复自去年下半年以来的稳步下降趋…...

【头歌-Python】字符串自学引导
禁止转载,原文:https://blog.csdn.net/qq_45801887/article/details/137517279 参考教程:B站视频讲解——https://space.bilibili.com/3546616042621301 如果代码存在问题,麻烦大家指正 ~ ~有帮助麻烦点个赞 ~ ~ 字符串自学引导 …...
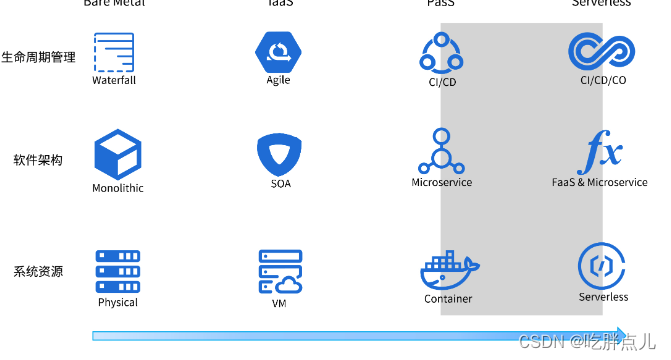
44-技术演进(下):软件架构和应用生命周期技术演进之路
应用、系统资源、应用生命周期管理这 3 个维度,构成了我们对云的所有诉求。 我会介绍下应用维度和应用生命周期管理维度的技术演进。 我们就先来看下软件架构的演进之路。 软件架构的演进 软件架构技术演进如下图所示: 单体架构 在单体架构中ÿ…...
【C++】C++中的list
一、介绍 官方给的 list的文档介绍 简单来说就是: list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中…...

uniapp:Hbuilder没有检测到设备请插入设备或启动模拟器的问题解决
问题 使用模拟器调试运行项目时,出现以下提示,“没有检测到设备,请插入设备或启动模拟器后点击刷新再试”。排查了一天最终找到原因。 解决 已确认模拟器是已经正常启动,并且Hbuilder设置中的adb路径和端口都配置没有问题&#…...
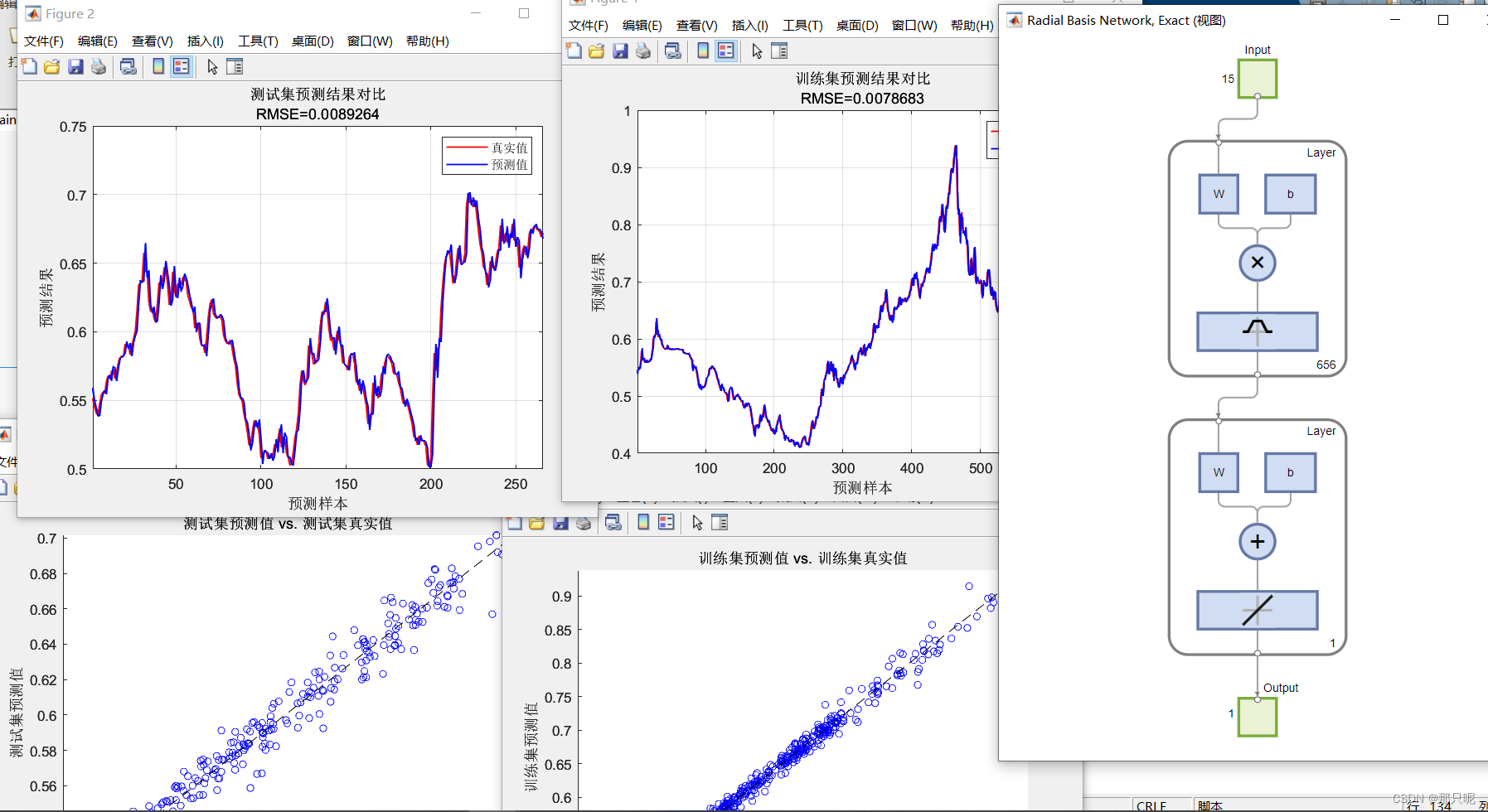
基于RBF的时间序列预测模型matlab代码
整理了基于RBF的时间序列预测模型matlab代码, 包含数据集。采用了四个评价指标R2、MAE、MBE、MAPE对模型的进行评价。RBF模型在数据集上表现非常好。 训练集数据的R2为:0.99463 测试集数据的R2为:0.96973 训练集数据的MAE为:0.…...
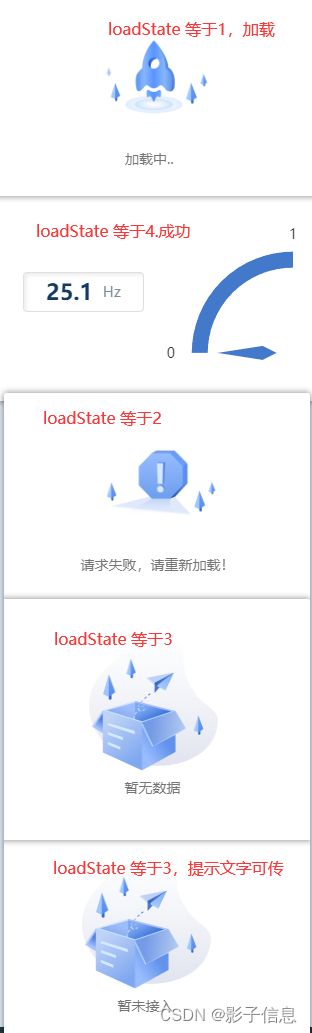
vue vue3 手写 动态加载组件
效果展示 一、需求背景: # vue3 项目涉及很多图表加载、表格加载 #考虑手写一个动态加载组件 二、实现思路 通过一个加载状态变量,通过v-if判断,加载状态的变量等于哪一个,动态加载组件内部就显示的哪一块组件。 三、实现效果…...

HTML:表单
目录 案例: 一、form标签 二、input标签 三、textarea标签 四、select标签 五、fieldset 标签 案例: <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>报名表</title> </head> &l…...

即插即用篇 | YOLOv5/v7引入Haar小波下采样 | 一种简单而有效的语义分割下采样模块
本改进已集成到 YOLOv5-Magic 框架。 下采样操作如最大池化或步幅卷积在卷积神经网络(CNNs)中被广泛应用,用于聚合局部特征、扩大感受野并减少计算负担。然而,对于语义分割任务,对局部邻域的特征进行池化可能导致重要的空间信息丢失,这有助于逐像素预测。为了解决这个问题…...
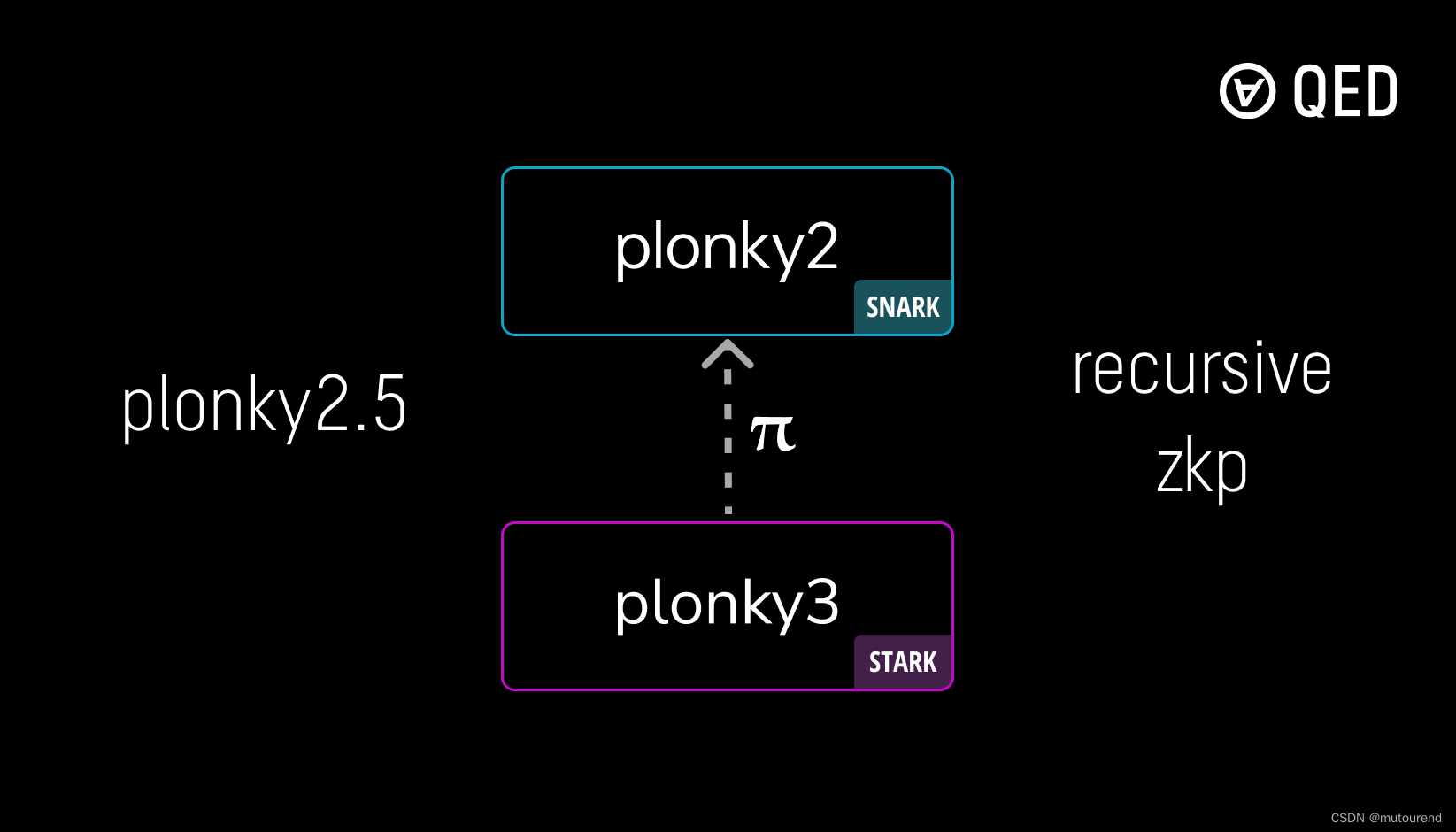
Plonky2.5:在Plonky2中验证Plonky3 proof
1. 引言 Plonky2.5为QED Protocol团队主导的项目,定位为: 在Plonky2 SNARK中验证Plonky3 STARK proof。 从而实现Plonky系列的递归证明。 开源代码实现见: https://github.com/QEDProtocol/plonky2.5https://github.com/Plonky3/Plonky3&a…...

卷积通用模型的剪枝、蒸馏---剪枝篇(此处以deeplabv3+为例,可根据模型自行定制剪枝层)
之后的两篇文章是对前段时间工作的一个总结。 一、环境配置 1.1、文章以b导的代码为模板,环境配置比较简单(第二篇蒸馏篇结束后会放置剪枝蒸馏配置好的百度网盘链接),其他算法自行配置,在剪枝之前,需要保证算法能够在本地跑通。 B导链接: https://github.com/bubbliiiin…...
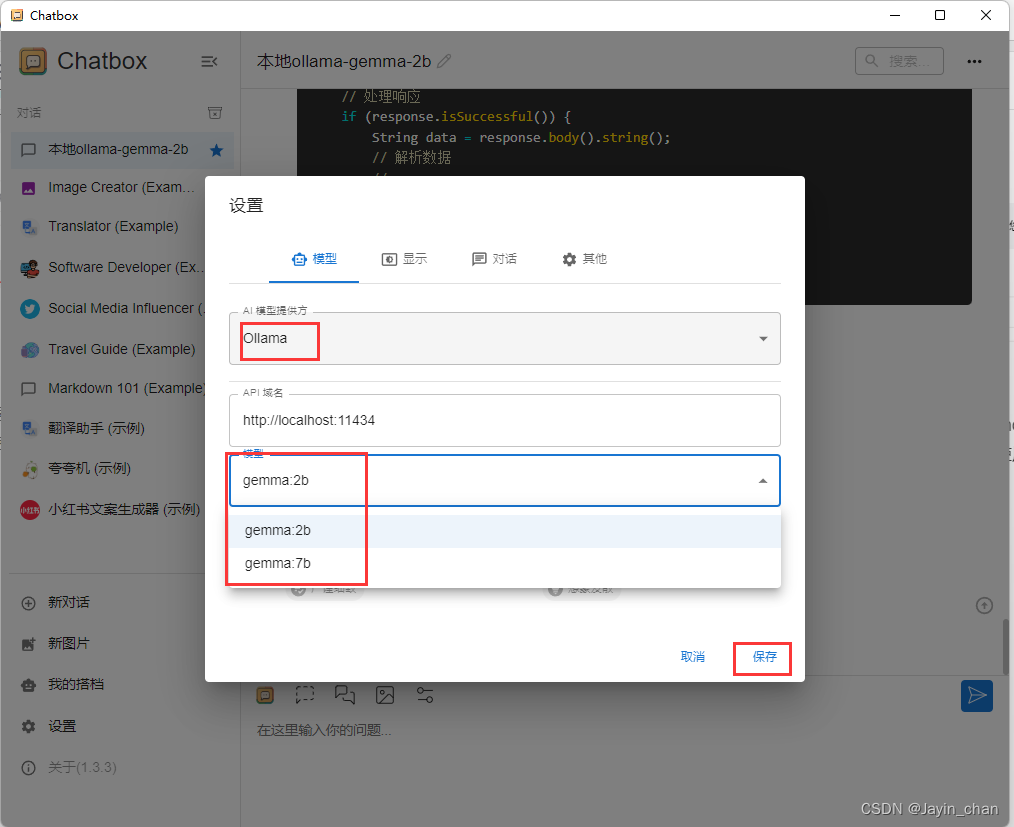
使用Ollama在本地运行AI大模型gemma
1.下载: https://github.com/ollama/ollama/releases 2.配置环境变量 我的电脑-右键-属性-系统-高级系统设置-环境变量-【系统环境变量】新建 变量名:OLLAMA_MODELS (固定变量名) 变量值:E:\Ollama\Lib ࿰…...

【IC前端虚拟项目】时序面积优化与综合代码出版本交付
【IC前端虚拟项目】数据搬运指令处理模块前端实现虚拟项目说明-CSDN博客 到目前为止,我们完成了第一版综合,那么就可以打开报告看一下了,一看就会发现在1GHz时钟下时序真的很差(毕竟虚拟项目里使用的工艺库还是比较旧的,如果用12nm、7mn会好很多): Timing Path Group cl…...
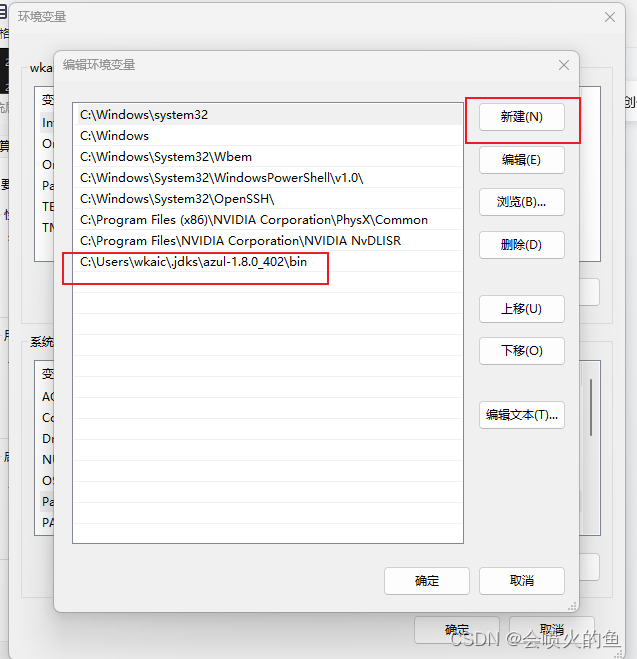
windows版本-idea中下载的java版本在哪
1、点击idea的file-projectStructure 进入: 通过电脑目录进入该目录 找到bin目录,copy该目录地址 copy下来之后设置到系统环境变量中...

设计模式:创建者模式
定义 创建者模式(Builder Pattern),又称建造者模式,是一种创建型设计模式,它提供了一种创建对象的最佳方式。该模式允许将一个复杂对象的构建与它的表示分离,这样同样的构建过程可以创建不同的表示。创建者…...
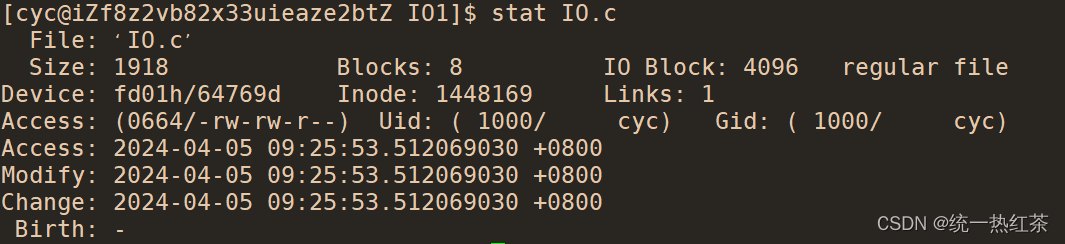
【linux】基础IO(四)
在上一篇基础IO中我们主要讲述了文件再磁盘中的存储,当然我们说的也都只是预备知识,为这一篇的文件系统进行铺垫。 目录 搭文件系统的架子:填补细节:inode:datablock[]: 更上层的理解: 搭文件系统的架子&a…...
蓝桥杯习题)
集合框架(数组,Arrays.sort,list,map,set,stack,queue)蓝桥杯习题
前言(基本知识) List集合 有序,接口, List<引用数据类型> listnew ArrayList<>(); 方法: add() size() get()//索引index从0开始,返回对应的值 isEmpty()判断是否包含该元素,不包含返回true,包含返…...
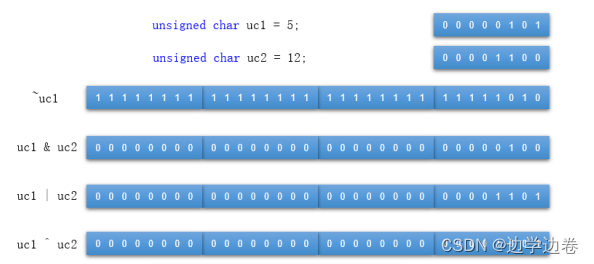
【C++基础】运算符和流程控制语句
C中的运算符和流程控制语句 一、运算符1. C和Java在通用运算符中的不同之处对比2. C中的位运算符2.1 移位运算符2.2 位逻辑运算符 3. 运算时的类型转换总结3.1 隐式类型转换3.2 显式类型转换(强制类型转换) 4. 注意 二、流程控制语句1. C和Java在通用流程…...

AOF文件重写
1.2.3.AOF文件重写 因为是记录命令,AOF文件会比RDB文件大的多。而且AOF会记录对同一个key的多次写操作,但只有最后一次写操作才有意义。通过执行bgrewriteaof命令,可以让AOF文件执行重写功能,用最少的命令达到相同效果。 如图&am…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
