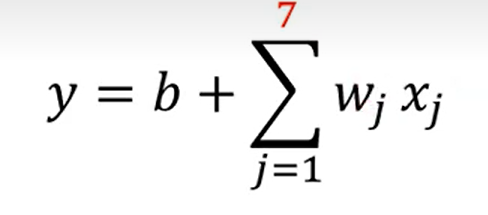机器学习和深度学习 -- 李宏毅(笔记与个人理解1-6)
机器学习和深度学习教程 – 李宏毅(笔记与个人理解)
day1
课程内容
- 什么是机器学习 找函数
- 关键技术(深度学习) 函数 – 类神经网络来表示 ;输入输出可以是 向量或者矩阵等
- 如何找到函数: supervised Learning 、 self supervised learning (pre train 又叫 Foundation Model 著名的例子有 Bert)、 Generative Adversarial Network、 Reforcement Learning
- 进阶内容 : Anomaly Detection 、 Explainable Al 、 Model Attack、 Domain Adaptation、NetWork Compression、 Life- Long learning 、 Meta Learning = learn to learn
Day2
introduction of Machine /deep Learning
Machine 是什么?
函数的不同类型
预测 分类
Structured learning 产生一个有结构的物件
一个例子 : Youtube Channel 的订阅量 找一个函数可以预测明天的观看次数
Step 1. y = w x1 +b Based on domain knowledge
Step 2. Define Loss From Training Data; Loss is a function of parameters L(b, w)
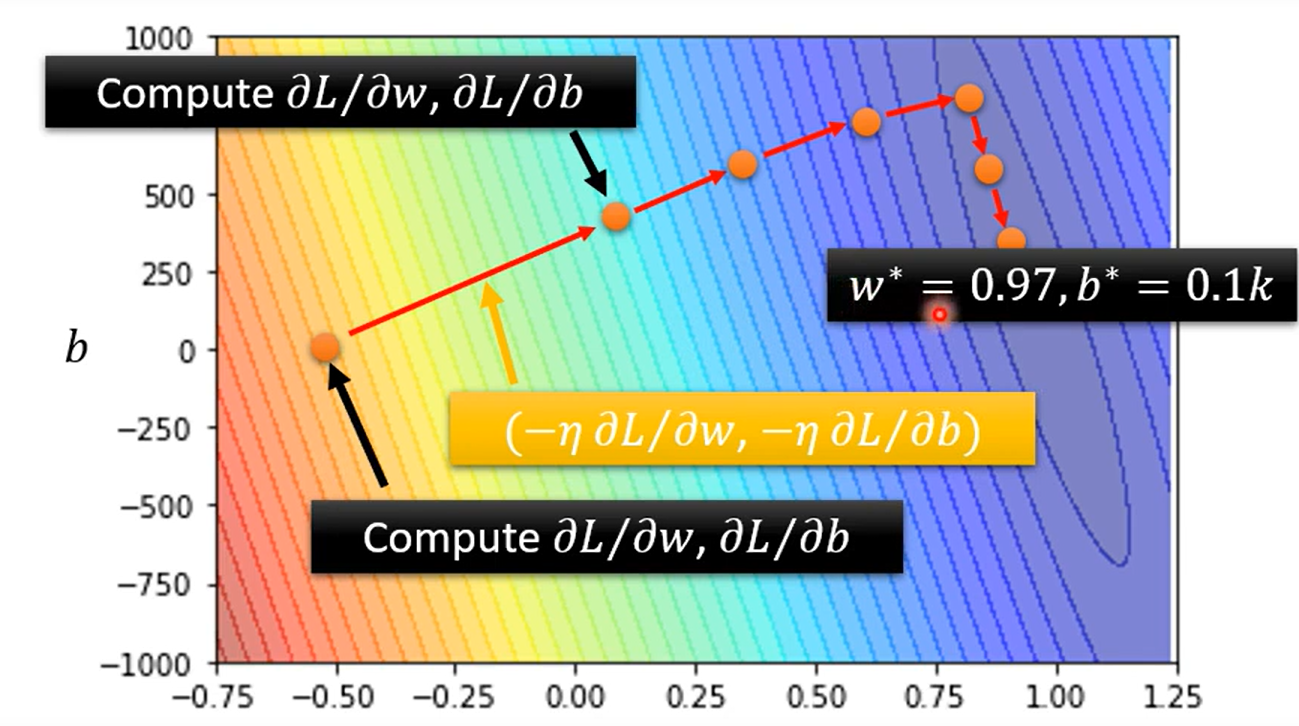
Step 3. Optimization w *, b * = arg min L ; Gradient Descent : 步长等于切线斜率(微分);然后还有一个n (ita)学习率来控制 w的变化长度 – > 通常自己设定hyperparameters
问题: 有可能陷入局部最优点; 可能的改进方法(self thinking)
1 取更好的初始点
2 改变学习率
3 找到所有的局部最优点(可以通过改变学习率进行跳出), 进行比较(例如找到十个不同的 局部最优点,然后进行min)
老师的伏笔: 高斯梯度 真正的痛点是什么?盲猜是 梯度消失 (wrong)
Gradient Descent
高斯梯度法的一般步骤: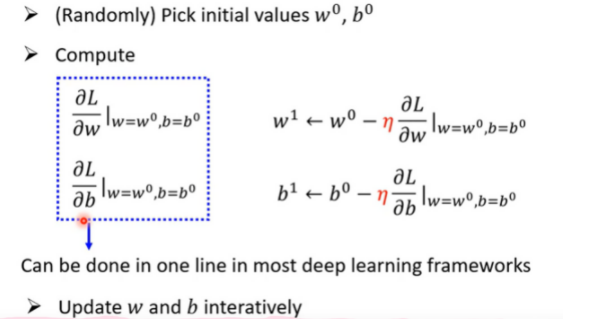
how to improve linear model?
因为 linear model 过于简单 造成了一定的 model bias; 需要有更多未知参数的model
如图所示 , 红色的线可以由 常数+ 一系列蓝色的线来拟合
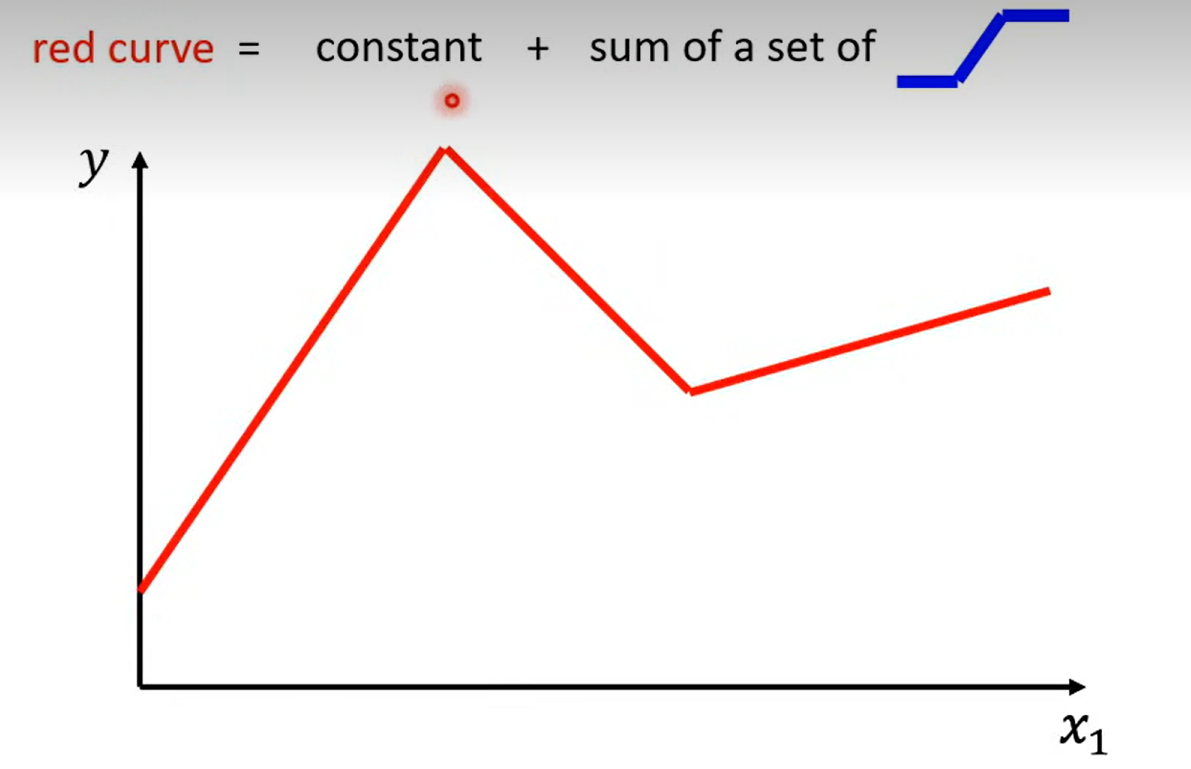
具体步骤如下:
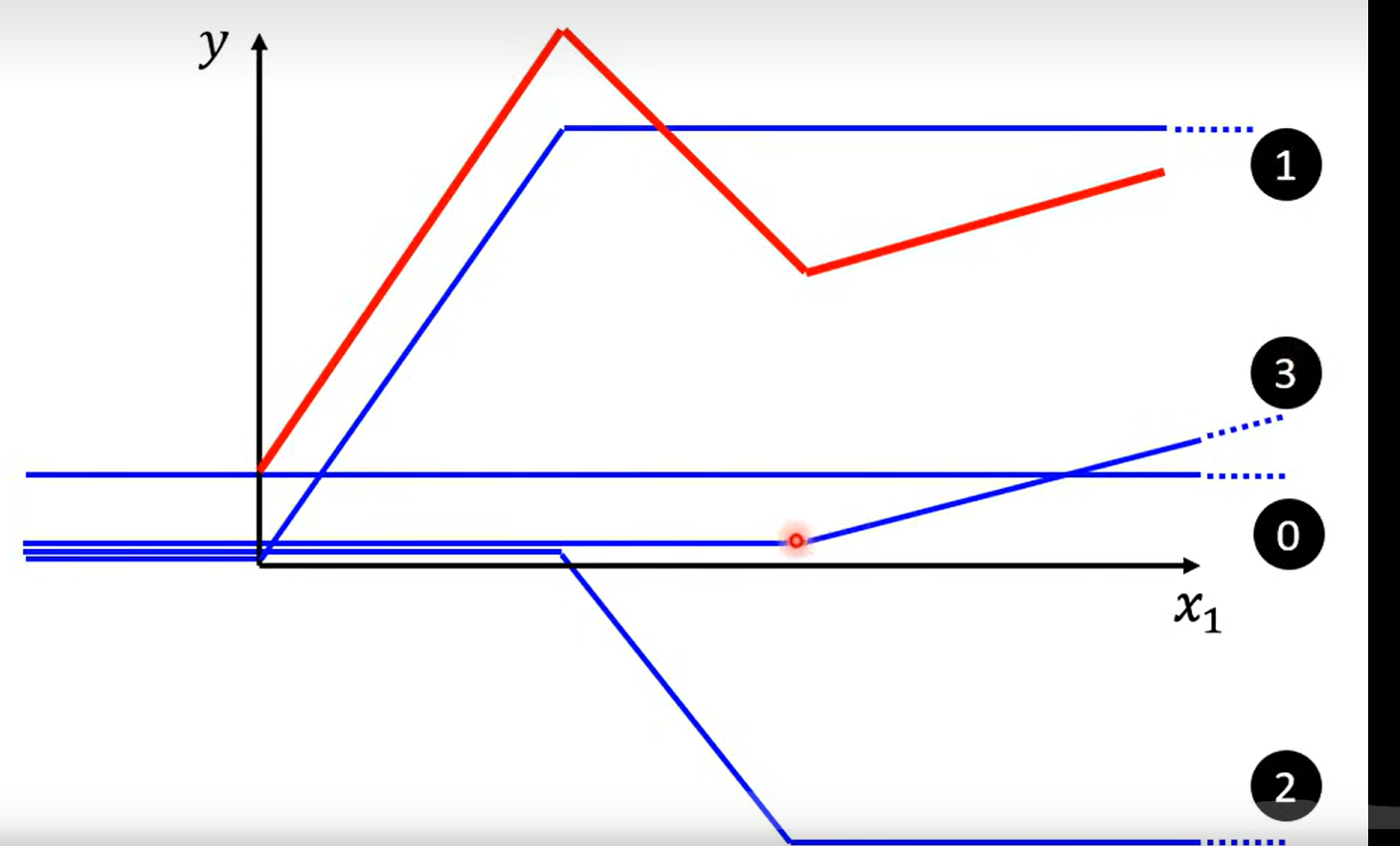
0+1+2+3 = red line
发现:
所有的piecewise linear curves 都可以由blue line 组成
发现 more:
beyond piecewise linear 也可以
how to represent this function (blue line )?
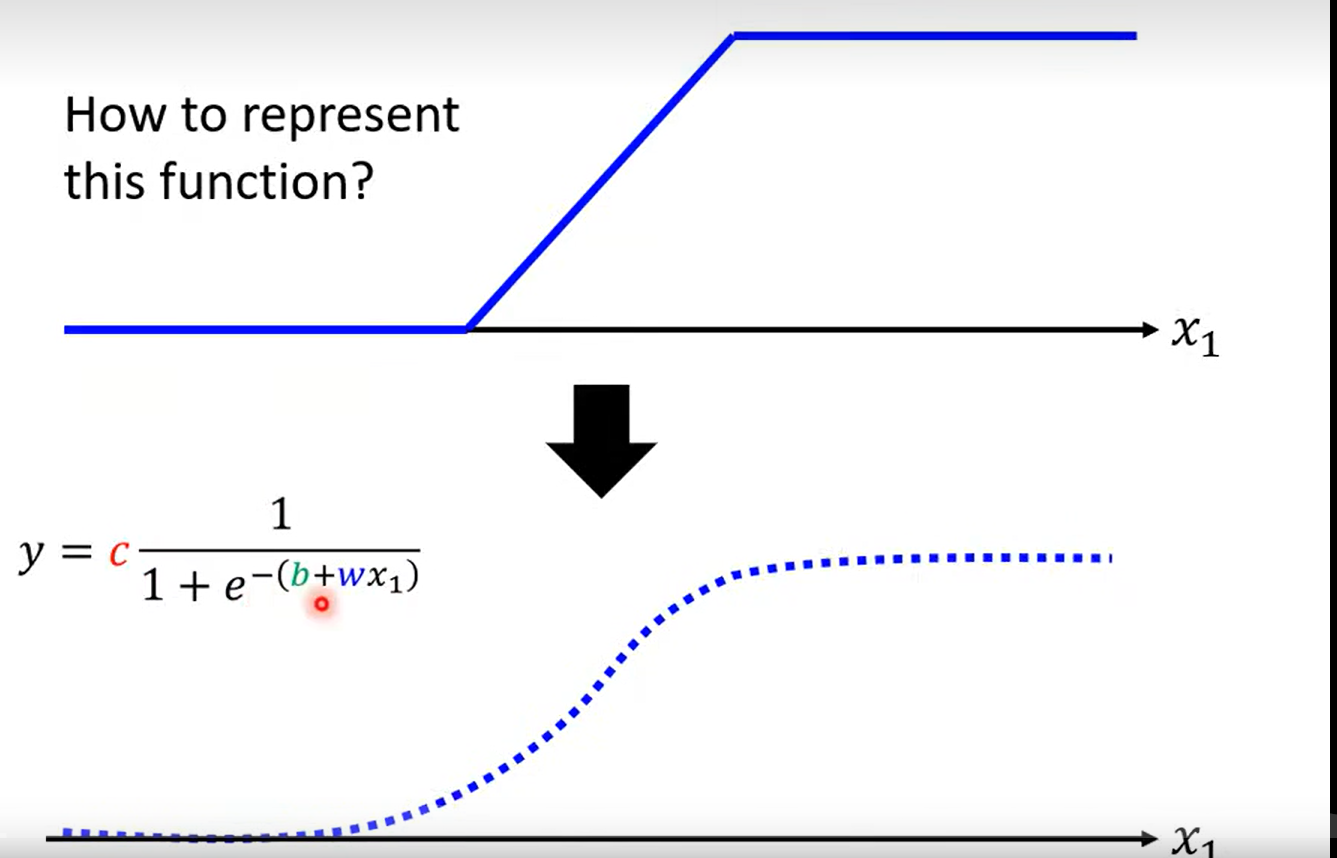
用一个近似的曲线表示 sigmoid function
more thinking:
- how to find the first sigmoid ? 数学变换?–> 人口增长的背景下,概率论中的伯努利分布 f(x|p)=px (1-p)1-x
- and w and b here 和 前面的linear functon 是否有关?无关
实际可用的拟合函数(折线函数)
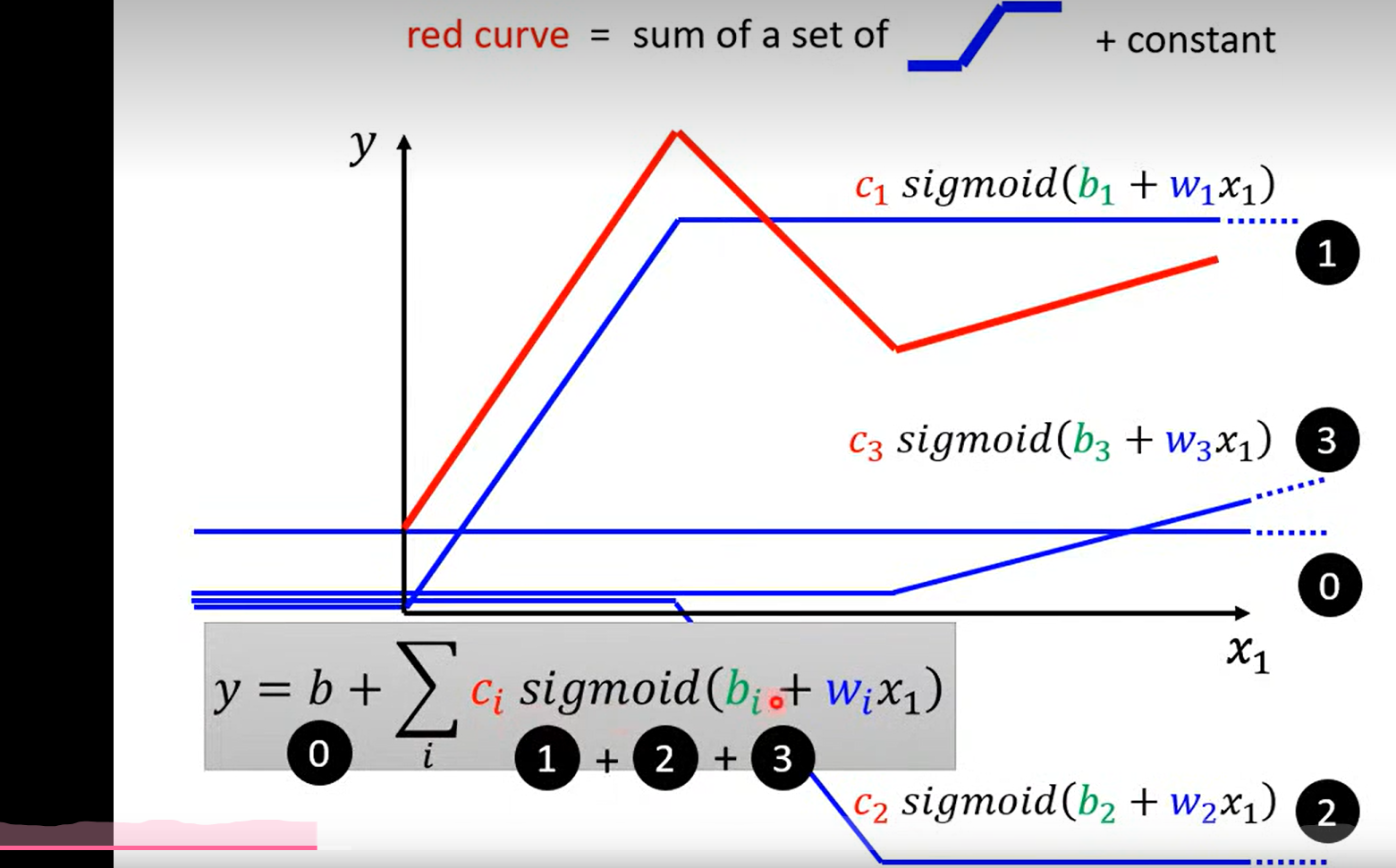
这里补充说明一点, 之前走了弯路, 以为这里的合成函数是一个分段函数, 后面的学习纠正过来, 这里就是单纯的 三个sigmoid 函数进行了 相加(有点多余, but who knows how could I say that )
NOw we have a new model which is more flexible
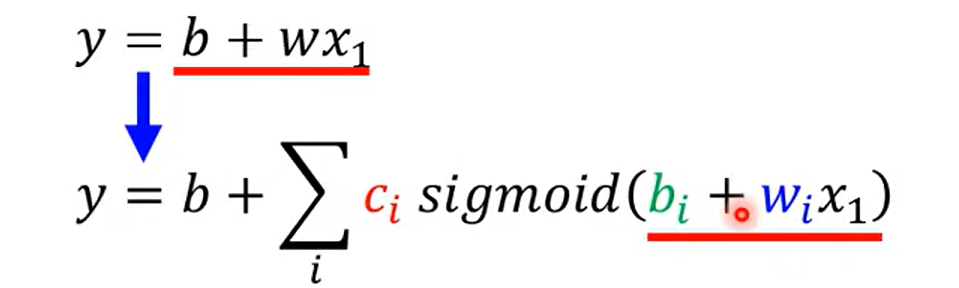
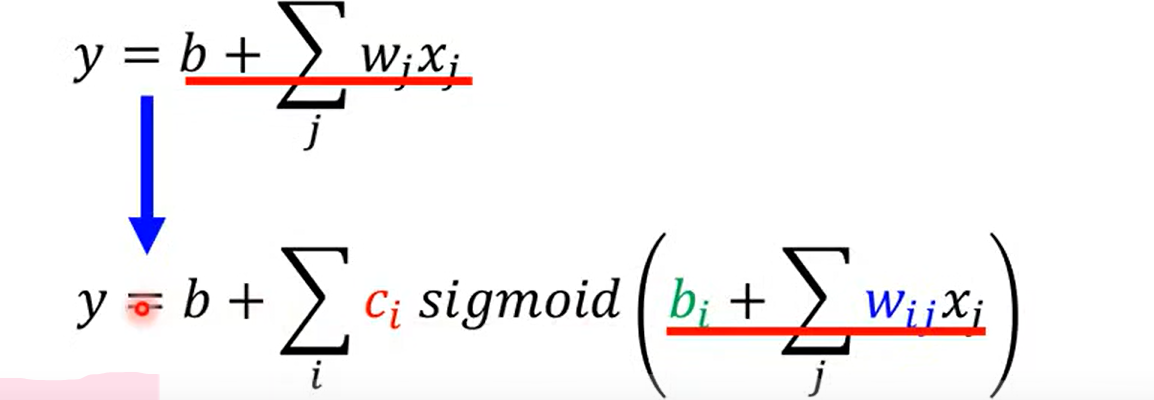
这里的w 表示特征,j表示特征的个数, 老师讲 如果是7天的话 j 就是1-7, 有一点点不明不白, 难道说之前的预测例子,是一个多特征的问题吗?
回忆, 好像确实和之前的linear model 有一点点不同, 一开始 取前一天,y = wx1 +b;后来取前七天的时候
注意这里的x 表示前j天的订阅次数, w 和b 是需要拟合的参数,也就是说这里至少需要拟合出7 组不同的w 一共有8 个参数(加上 b)。是根据前七天的订阅量, 预估第八天,相当于前七天是 不同的特征,预测第八天的特征,虽然老师这里的例子是实数值;换一个例子来表示可以这样理解: 选西瓜判断好坏瓜, 一开始只选择颜色(取值有 012 ),后来加上了 大小、响度,气味等不同的性状(取值为 0 1 2 ),然后预测瓜的取值(0 / 1 ); 从这个角度理解, 这个玩意儿相当于训练出 不同特征对于 结果影响的权重! nice
得出结论, 是的老师之前讲的例子确实相当于一个多特征的例子 √
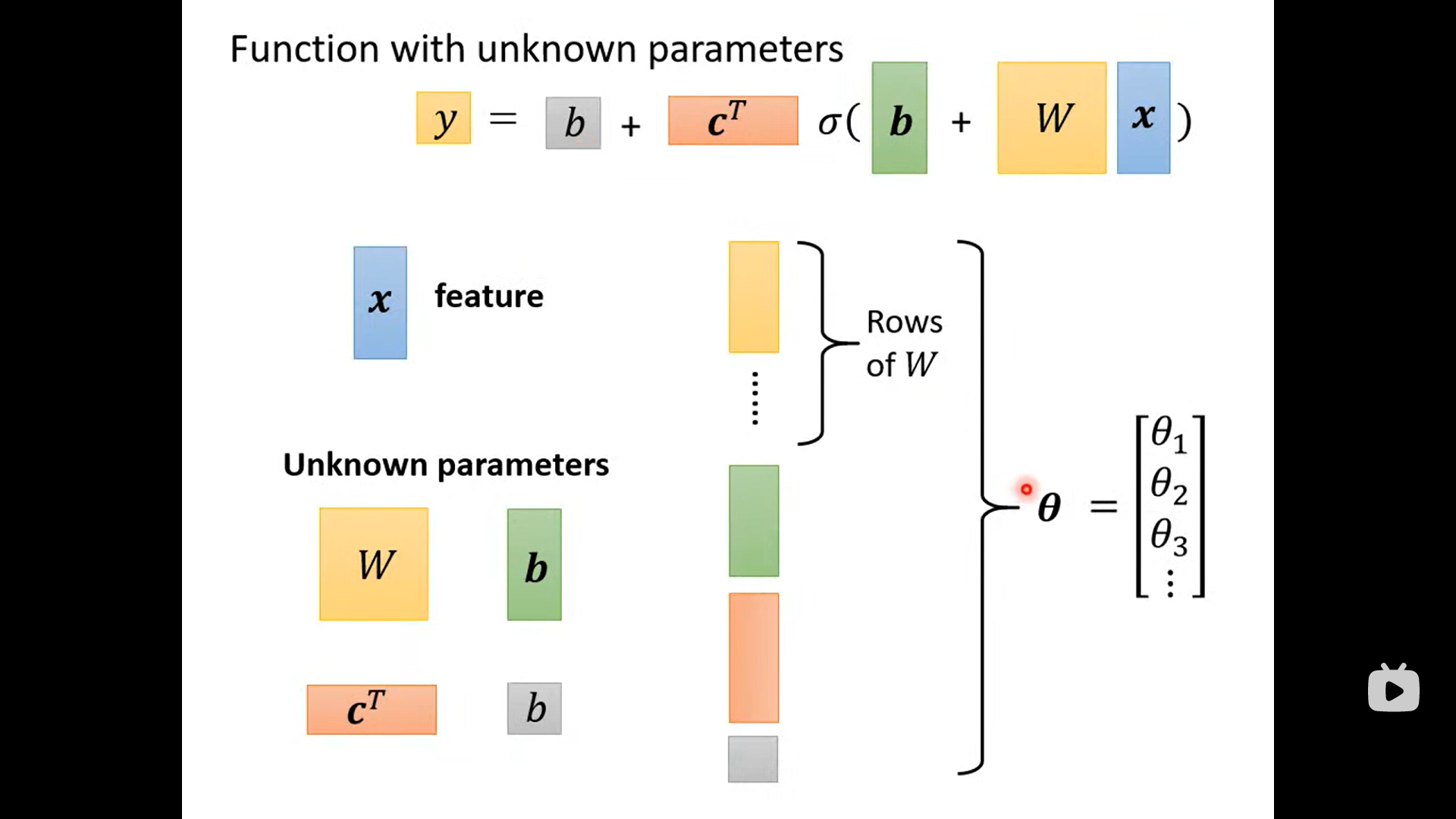
言归正传, 那么这里老师讲得到一个 关于w 的参数矩阵, 和b,c 的参数向量,以及 最外面的b ;
那么接下来的问题就变成,优化 这些参数使得 L 最小 (nice!)
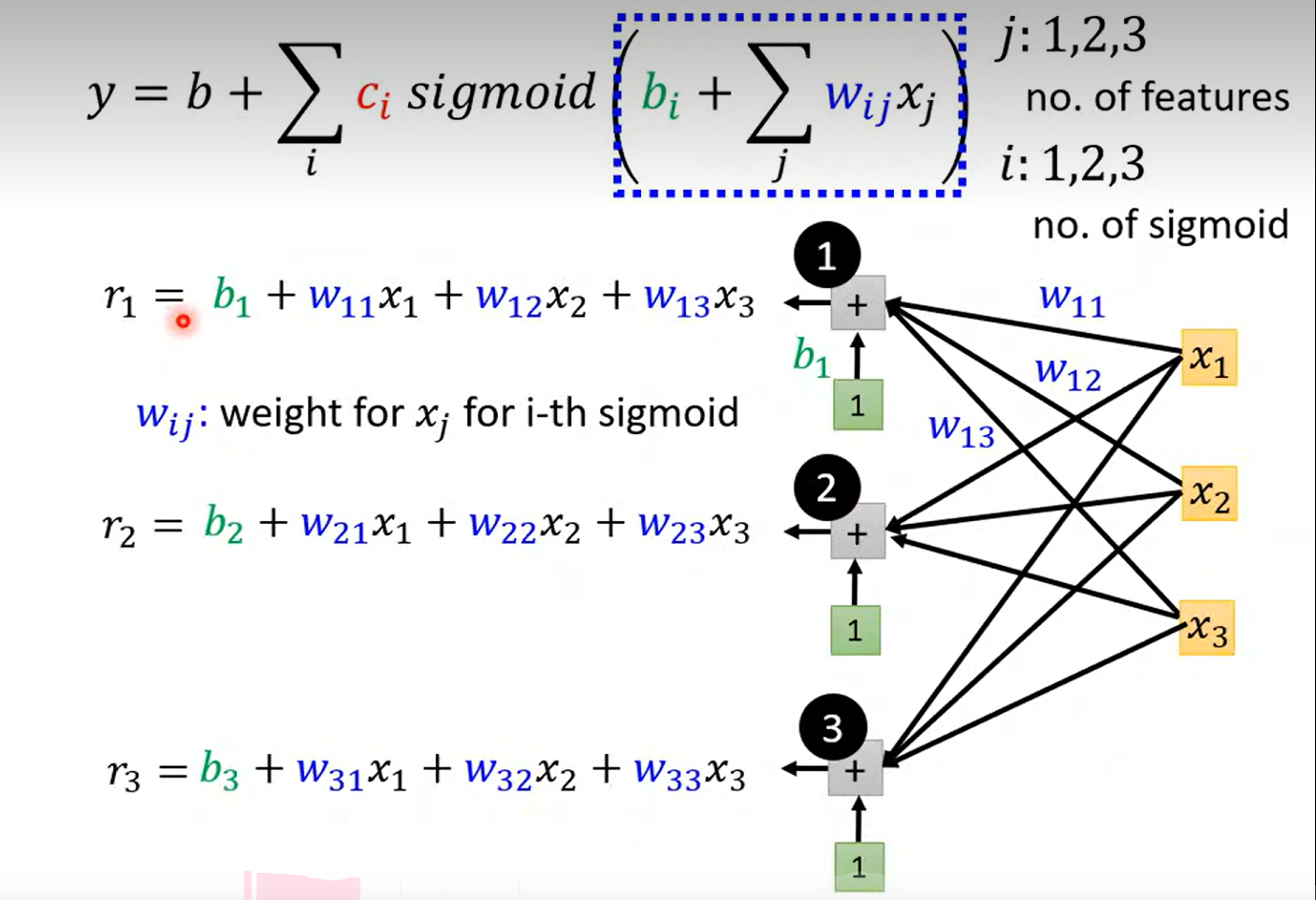
卡住了;
简单顺一下这个图是什么意思: x 表示前 1 2 3 天 的订阅量;
当 j 不变的时候, j = 1 ,表示,通过三个 blue line
去拟合 前一天的订阅量和y(第二天的订阅量)的关系;需要 3*3 +1 = 10 个参数; j = 2 / 3 的时候同上, ok pass ~
注意:w i j _{ij} ij 在这里表示每一个blue line 的斜率,w i j _{ij} ij表示每一个特征在每一次sigmoid 函数中所占的权重
more thinking :
这里的r1 ~r3 表示什么呢?根据式子来理解, 就只能是三种sigmoid 函数方法占预测结果的权重了
Day3
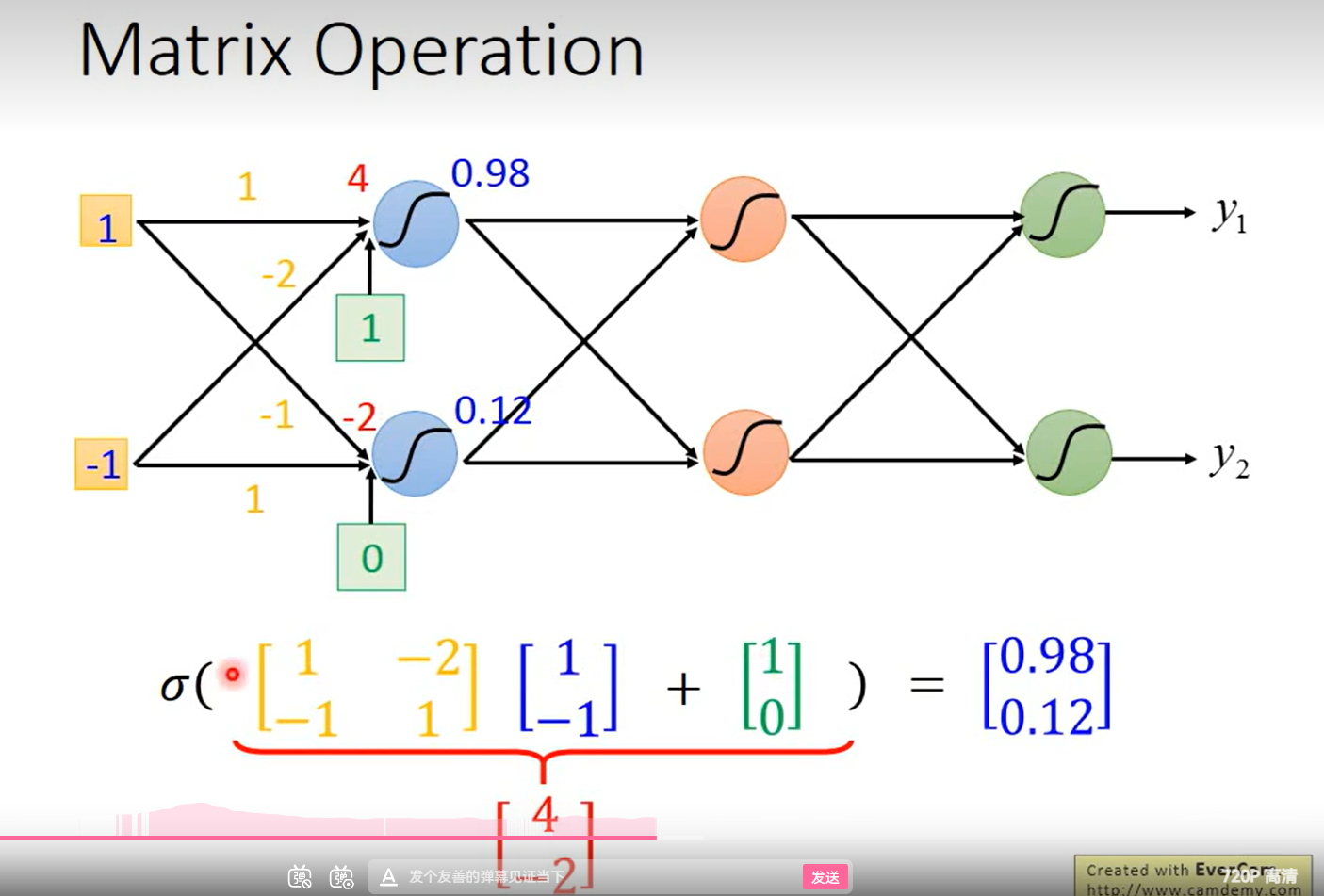
改写为向量和矩阵乘法的格式
接下来就分别把r 放到sigmoid方式里
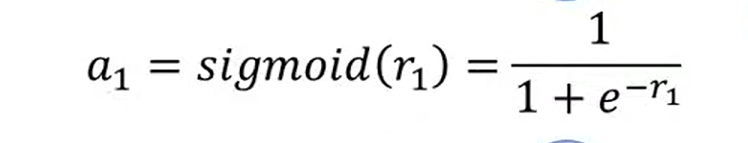
简写以后 (向量化)
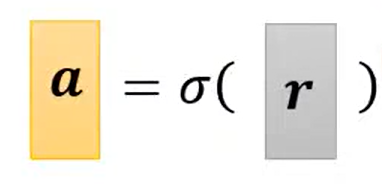
整个过程的向量表示: y = b + cT a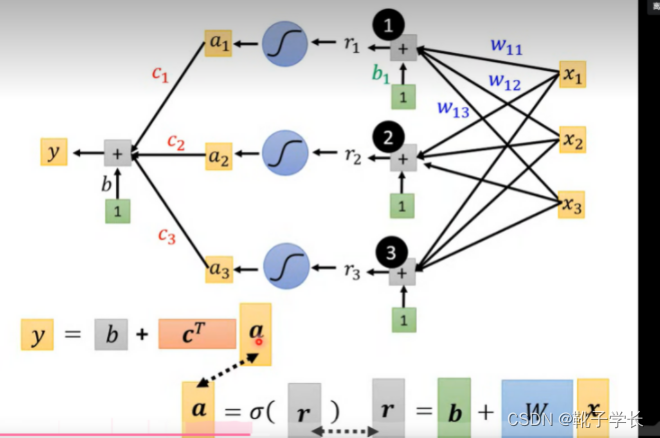
一系列线性代数的表示方法(简洁)
Before we find the parameter (unknown) ,define some variable
Loss L(theta)

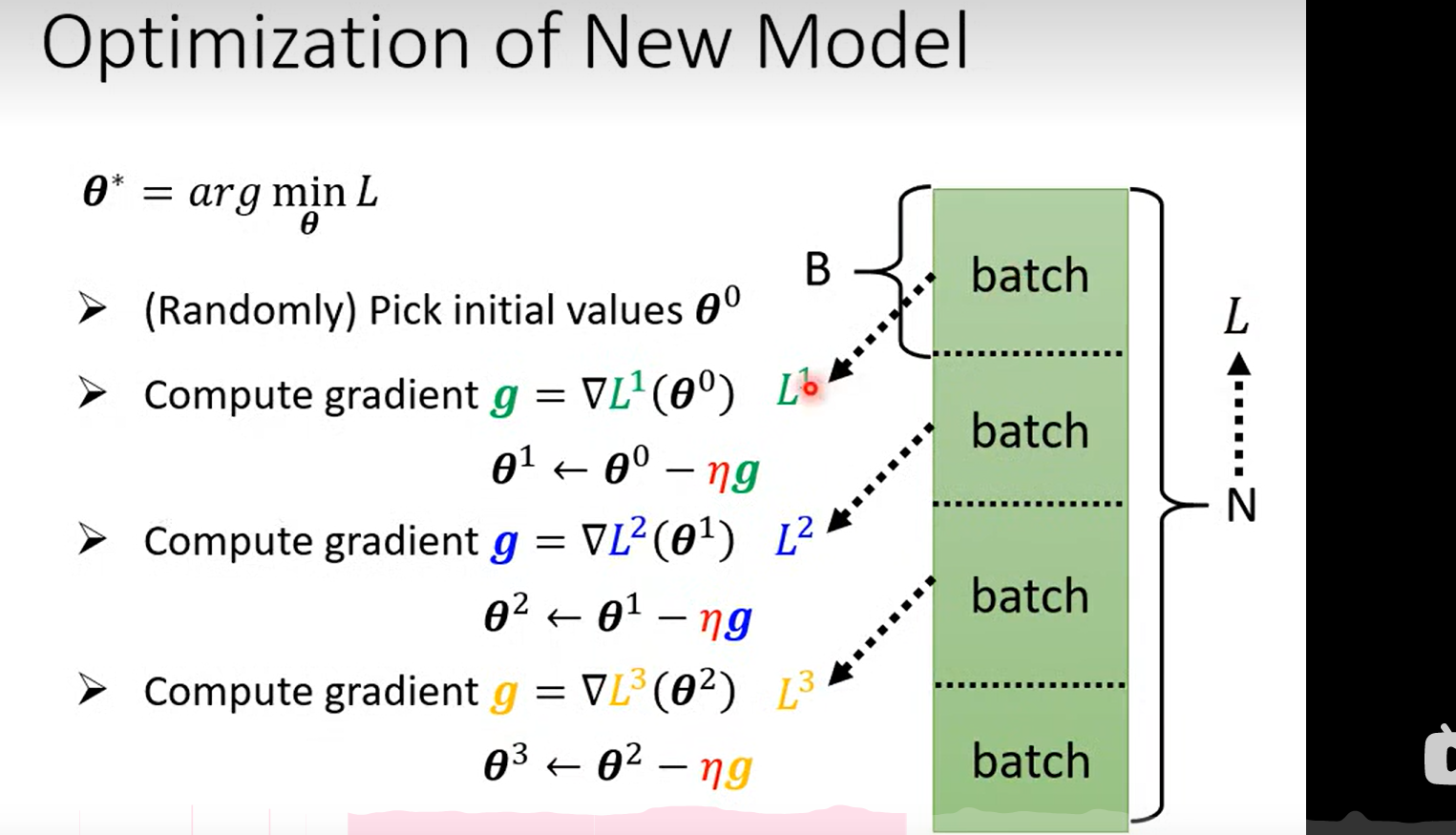
并不是用L 中的数据来训练参数,每一次更新参数的步骤叫做一次 epoch
Q:老师伏笔, 为什么这里要使用batch?
Day4
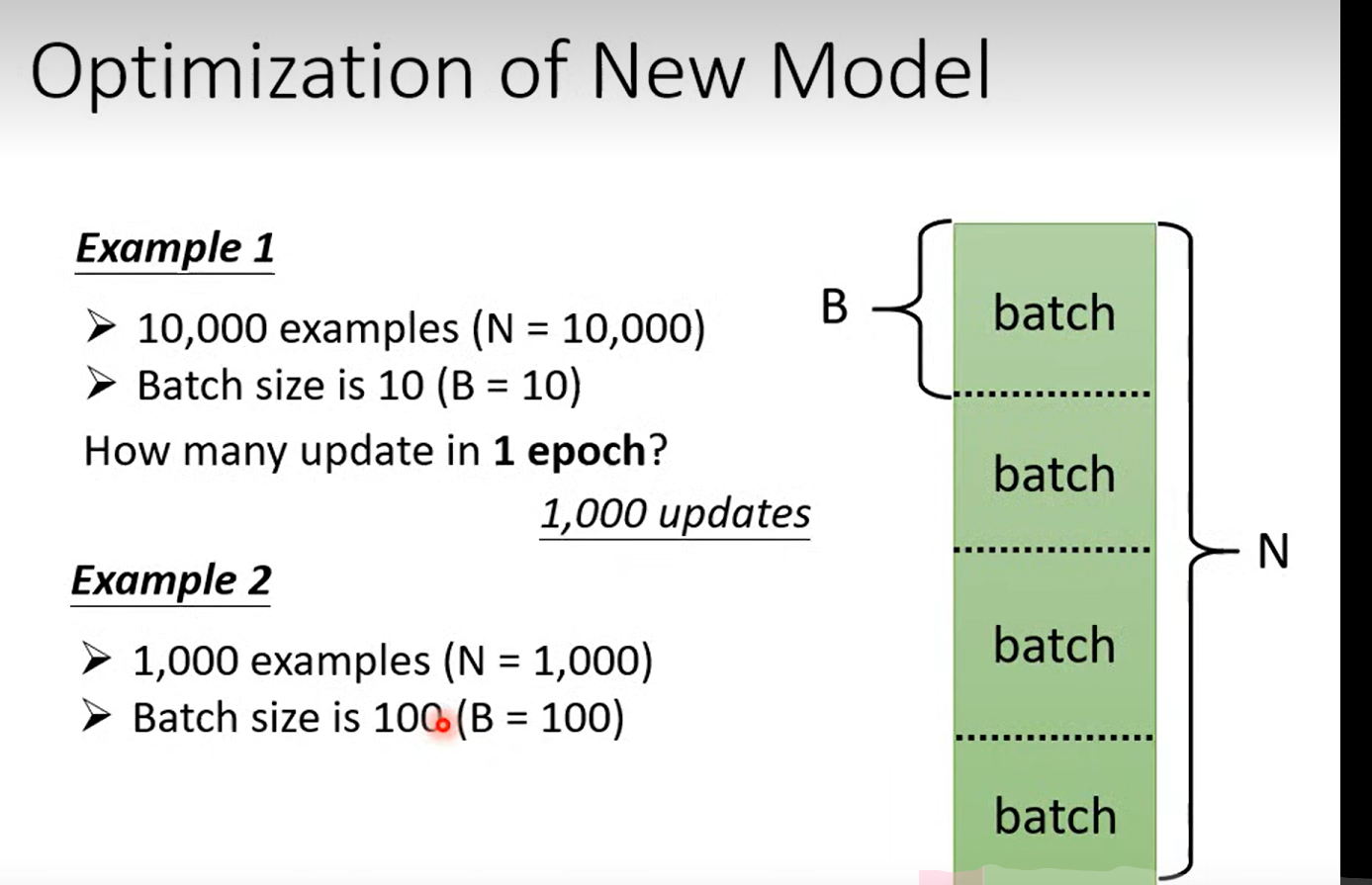
这里的batch Size 也变成了hyperparameter
一个hard Sigmoid 也等于两个relu的叠加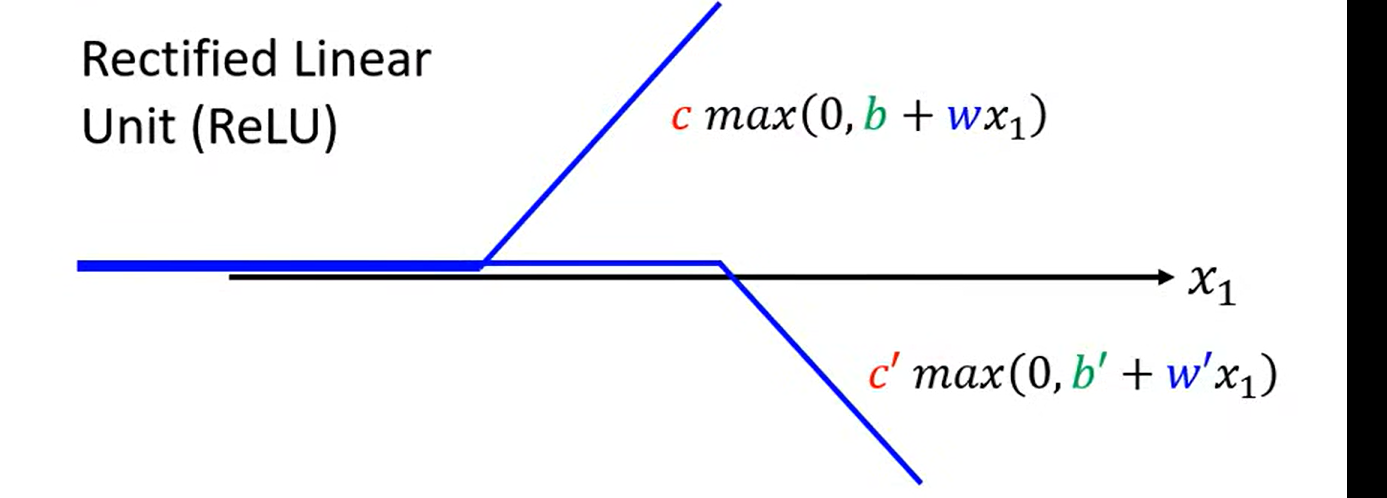
ActivationFunction
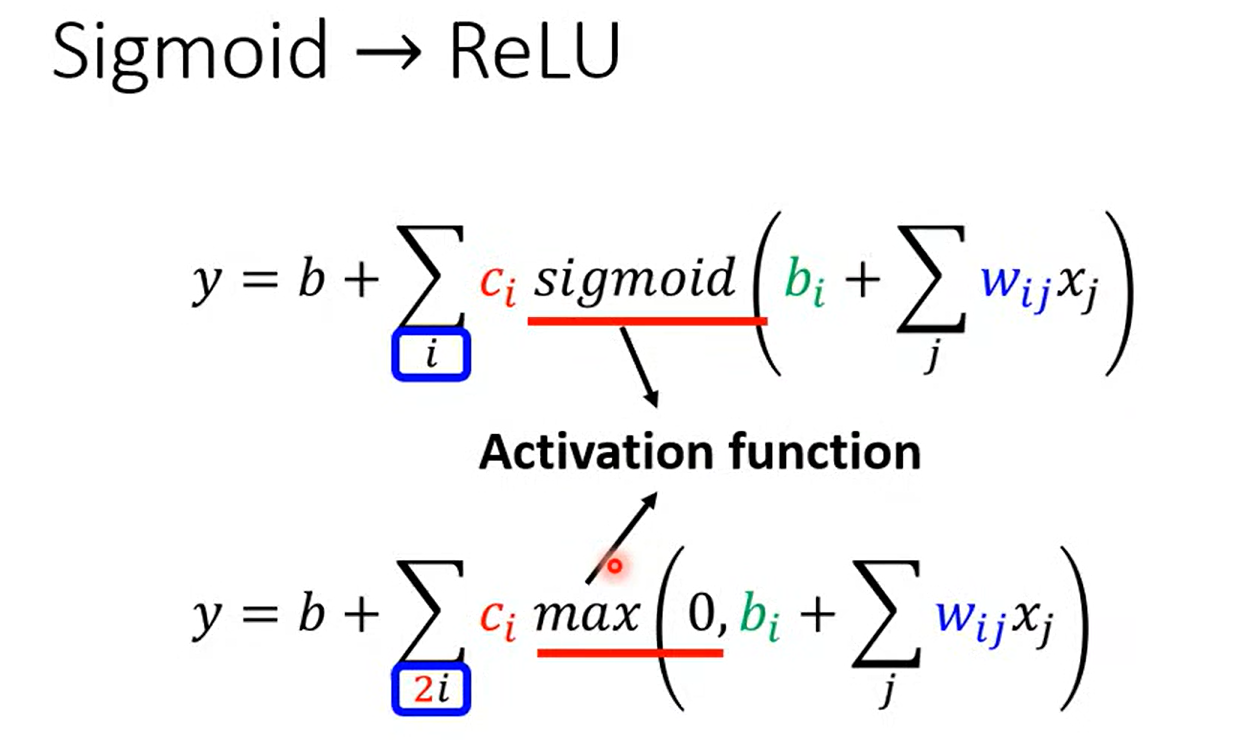
哪一种比较好?
神经网络训练的层数-- 又一个 hyperparameter
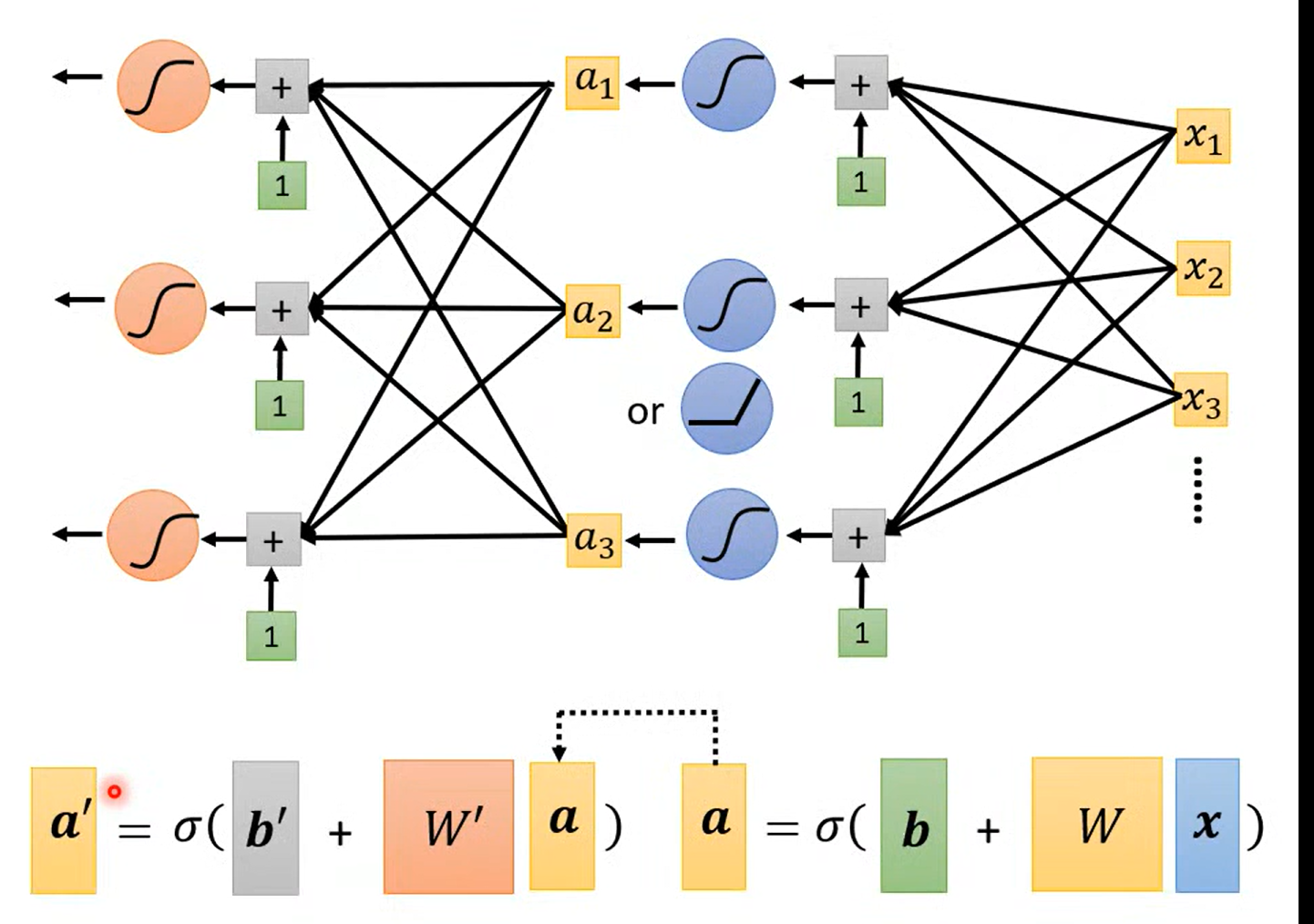
a fancy name
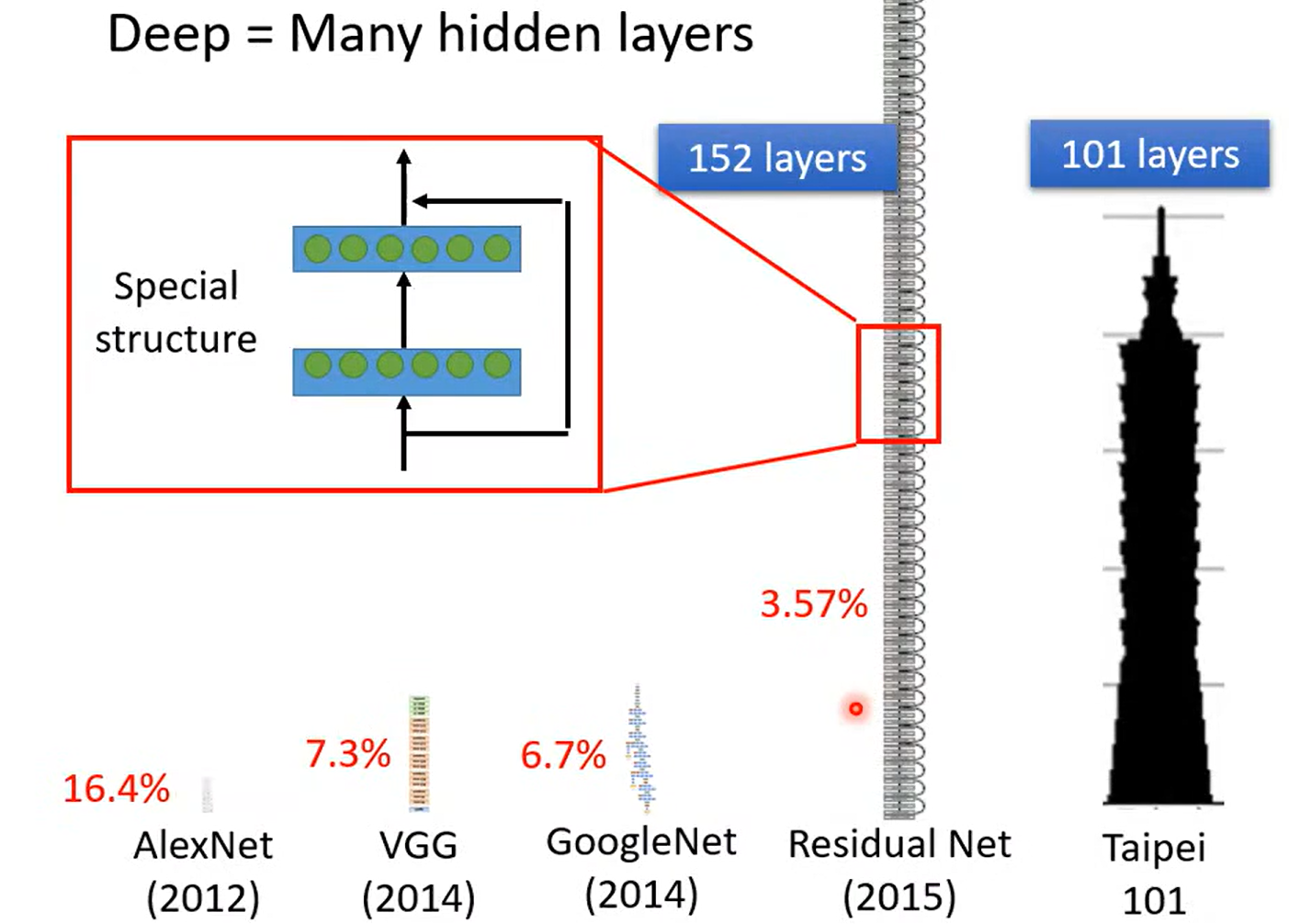
为什么深? 而不更宽呢
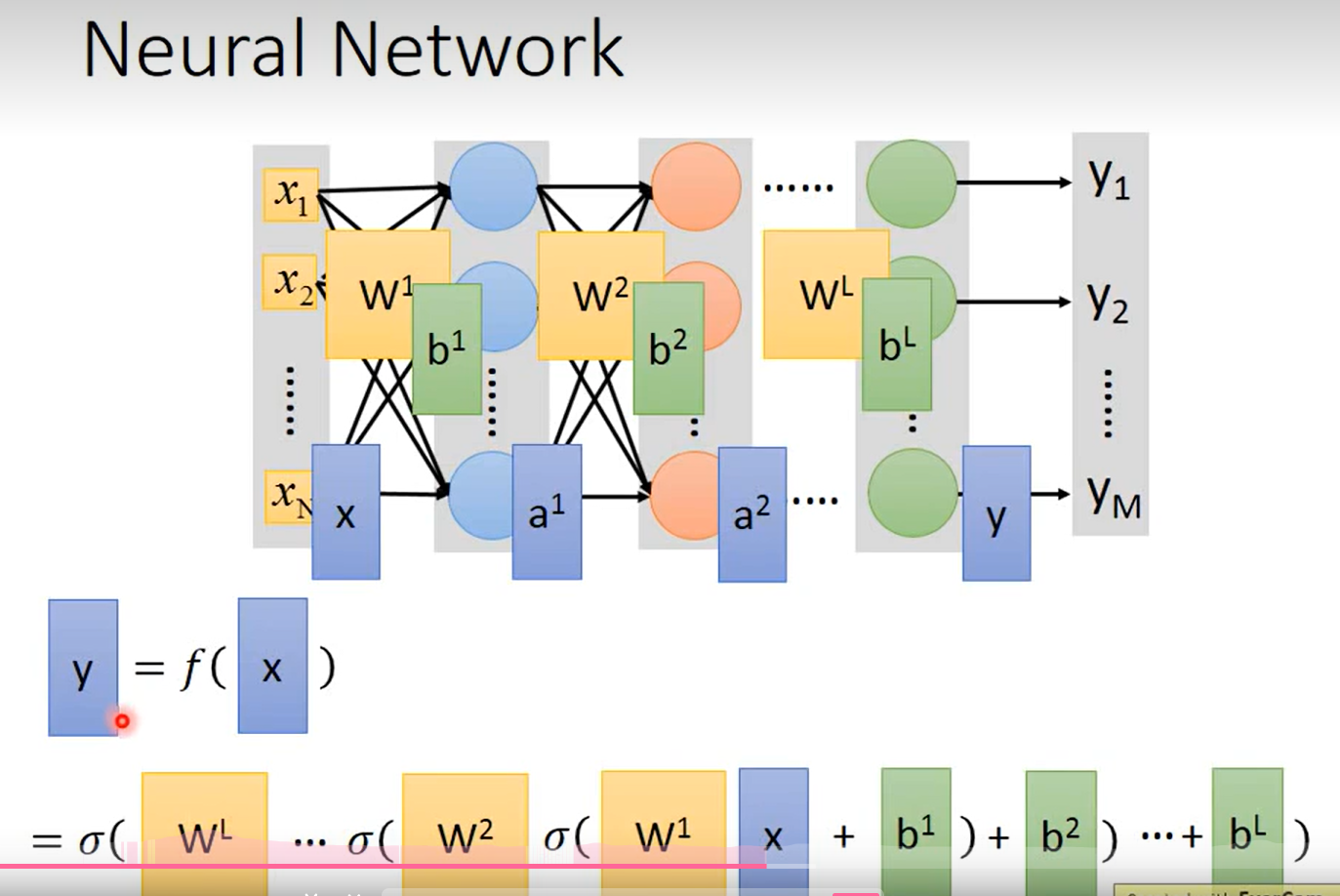
Fully connect feedforward
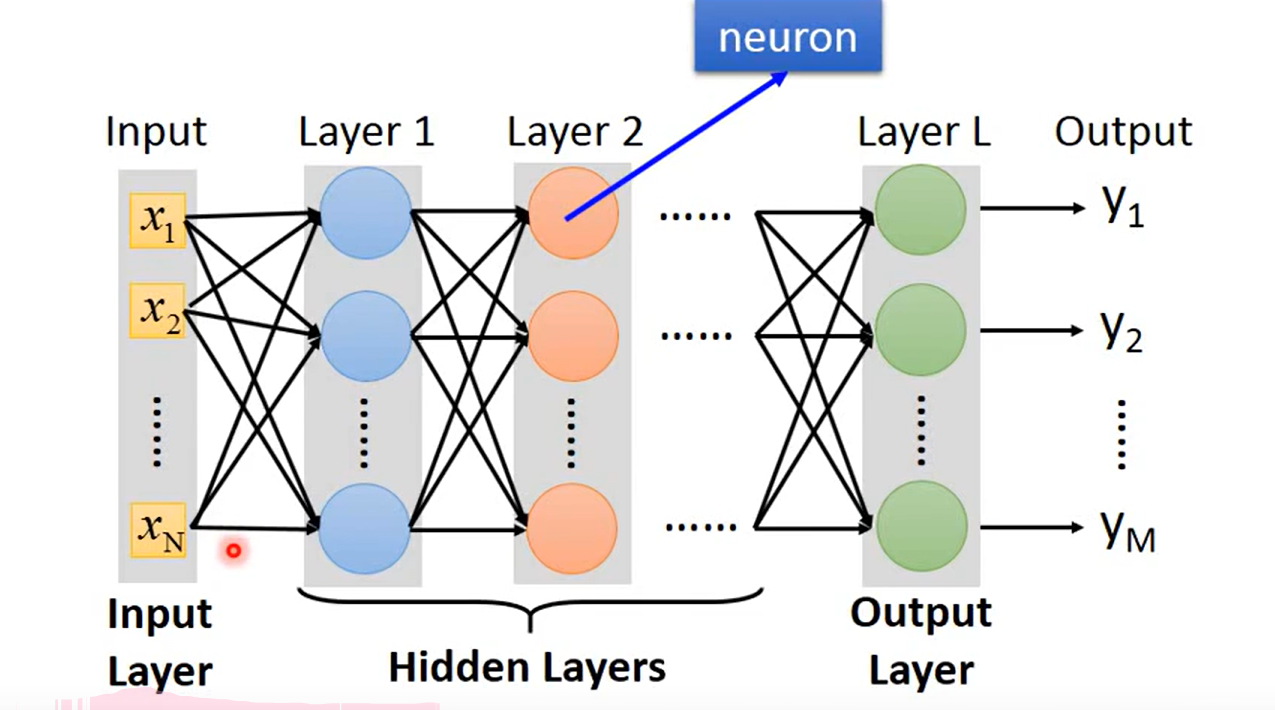
这里可以用来推导矩阵的表示
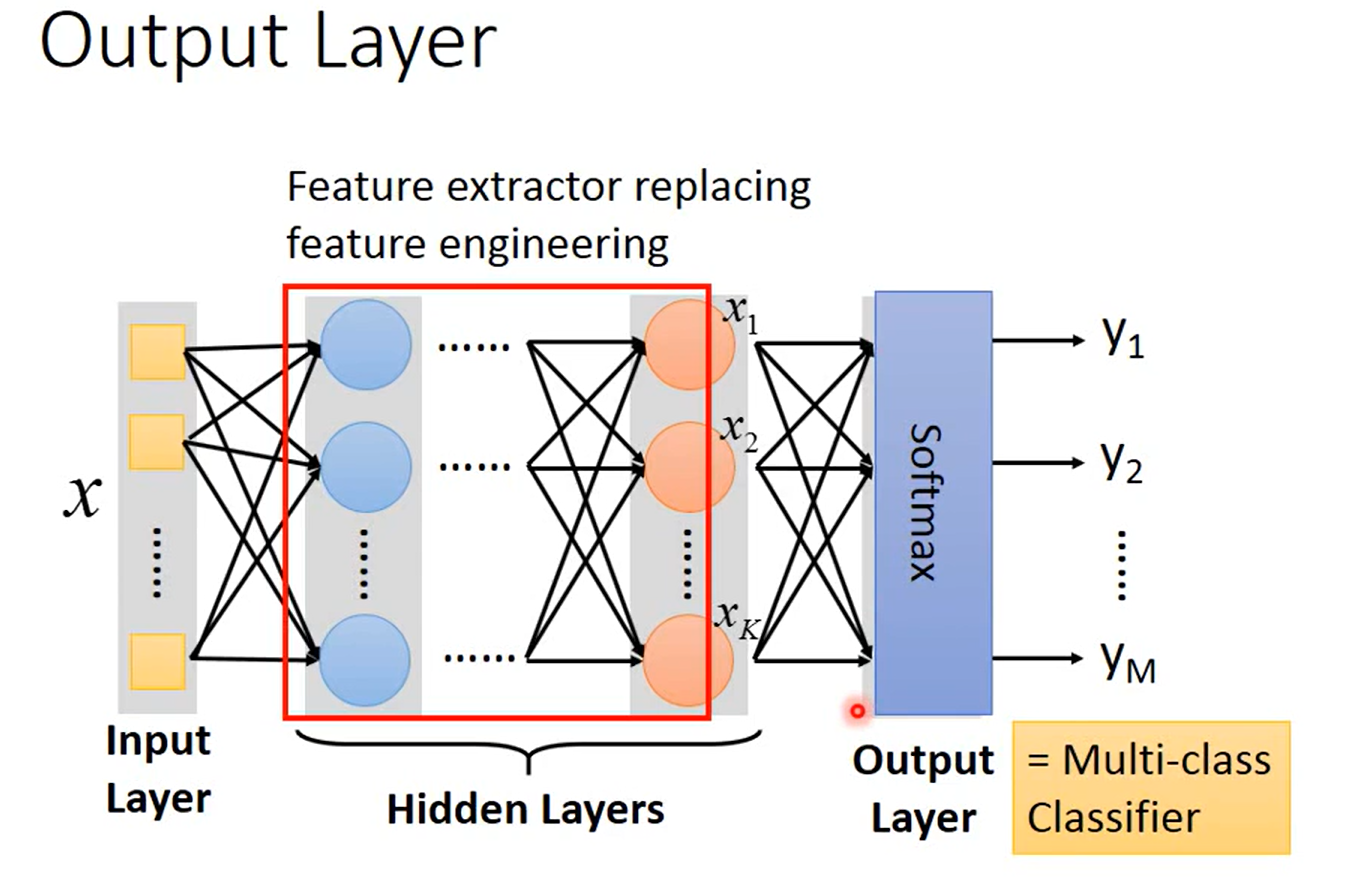
相当于在隐藏层中,做了特征提取;输出层相当于一个多分类器
FAQ
Loss 的定义
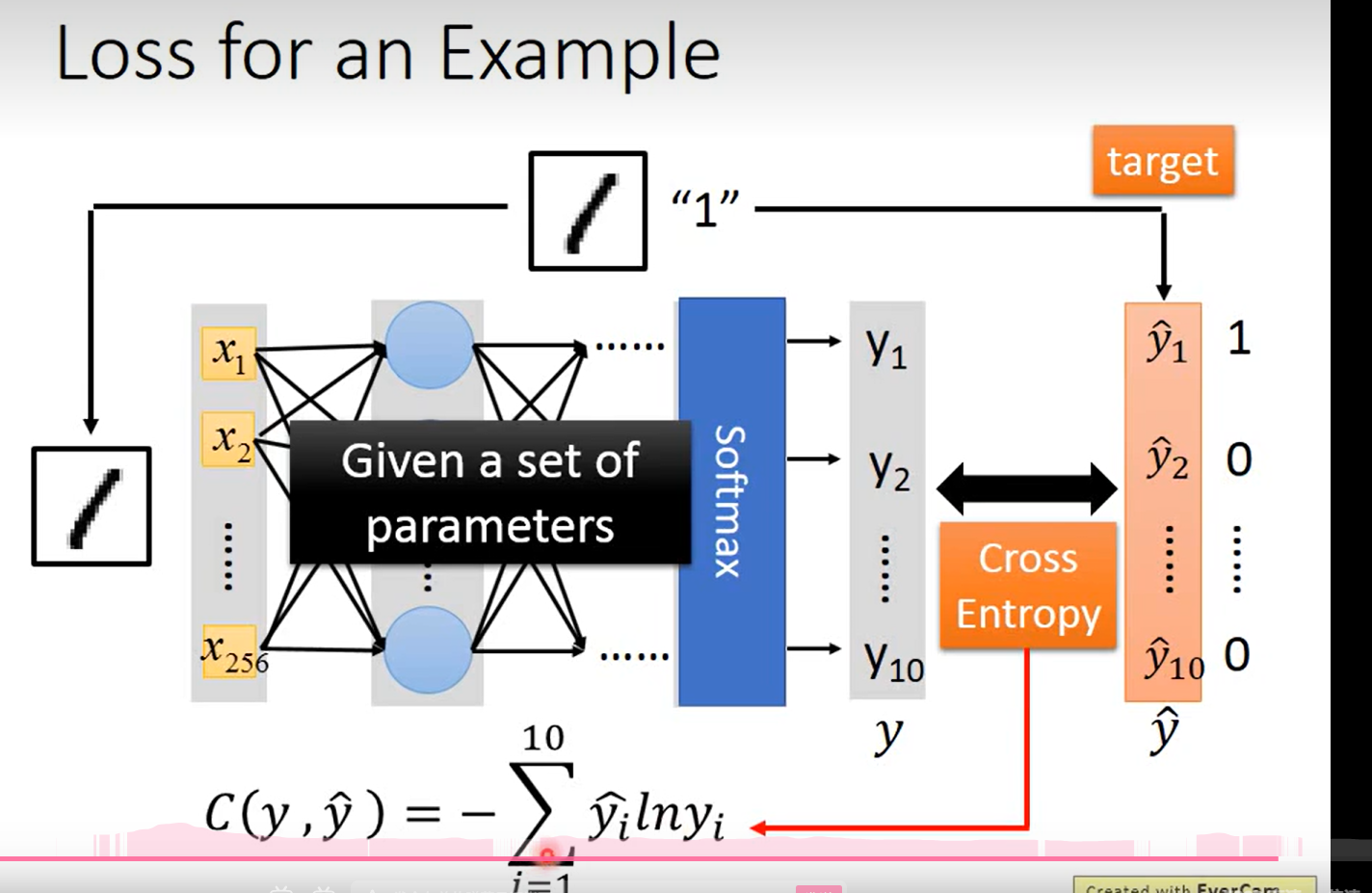
这里的这个函数用的很奇怪,没见过,但是简单分析一下, 这个式子表示的还是y 和 y ’ 的差距;but含奇怪的一点是 这里老师说 让这个参数越小越好 ……不应该是越大越好吗?因为有一个 负号
明白了 应该就是越小越好, 这里老师拿一个多分类的问题举例,所以这里用到了交叉熵的概念, 信息熵越小, 说明信息的混乱程度越小, 分类的 y1 --y10 越精确,之后的loss 见下一页ppt
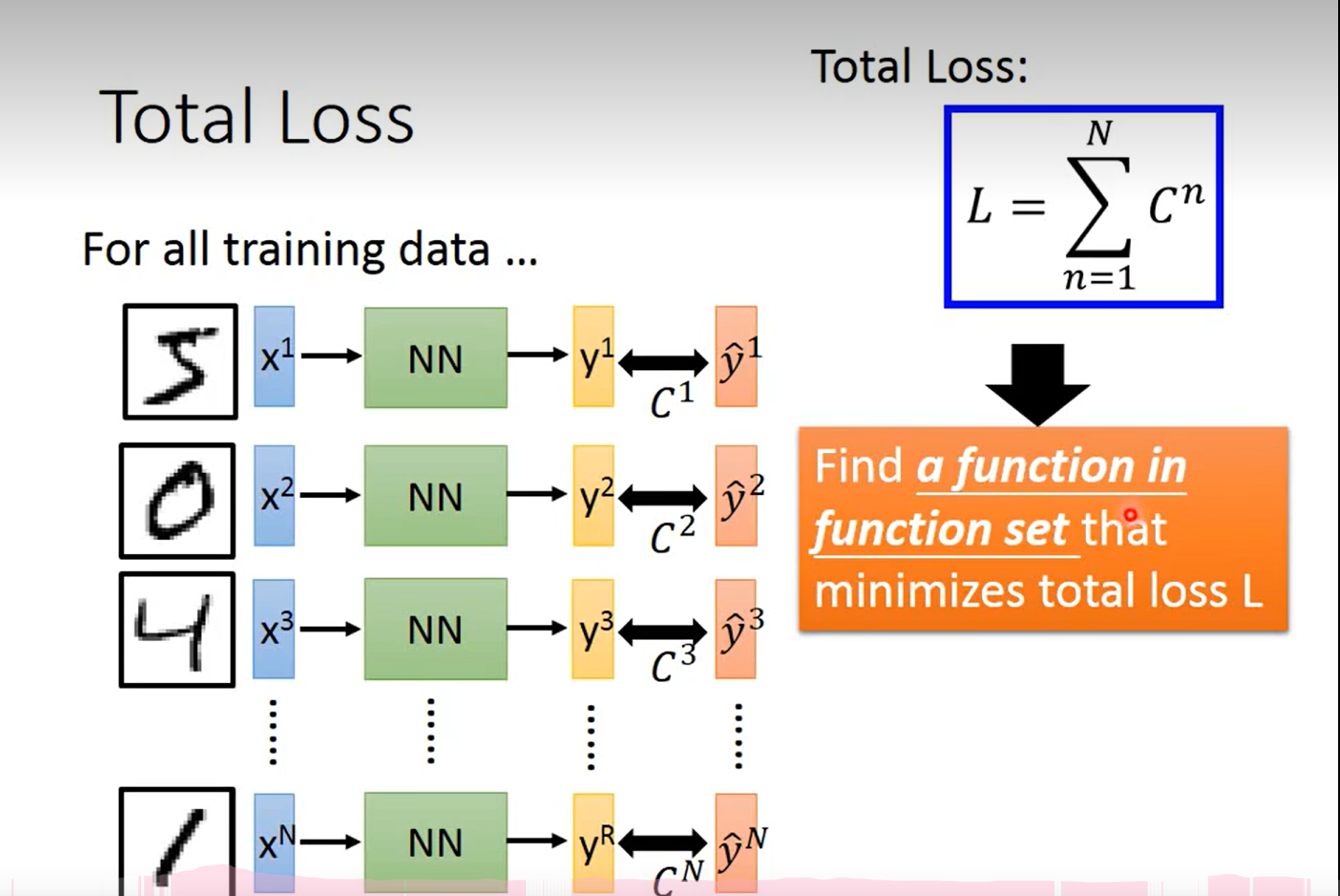
啊 这里Loss 为啥上面的系数是 n 啊…… 哦对,我sb,n表示的是c 的序号,而不是幂次;
怎么回事, 怎么乱糟糟的, 这个c i 到底是什么时候出现的?本质上还是对交叉熵的概念不了解导致的
交叉熵(cross Entropy)
…… 这个概念暂时悬而未解吧
这里注意一下哈,
首先这个交叉熵的概念先放下, 就先用最常见的欧氏距离来表示这里的 y 和y '的差距,ok,第一个问题解决了;
第二点, 为什么这里需要用c i 以及它表示的是什么意思, 简单理解的话就是说, 每一个输入对应的一个输出和真实值的距离;因此有多少组输入就会有多少个c
第三点, c 对w的偏微分 一定是 ci 到 cn 同时进行 且等于 0 的,否则不能保证他们的和最小 (c i 到cn的和)
Day5 BackPropagation
什么是方向传播?
在train neru network 的时候 GradientDiscent的运作方式
Gradient Descent

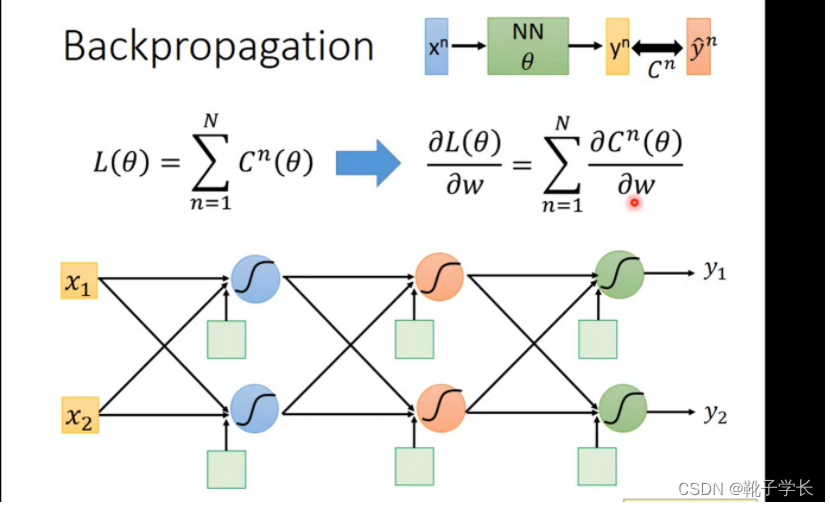
cn 表示 yn 和yn(head) 距离的function
chain Rule
正向传播:
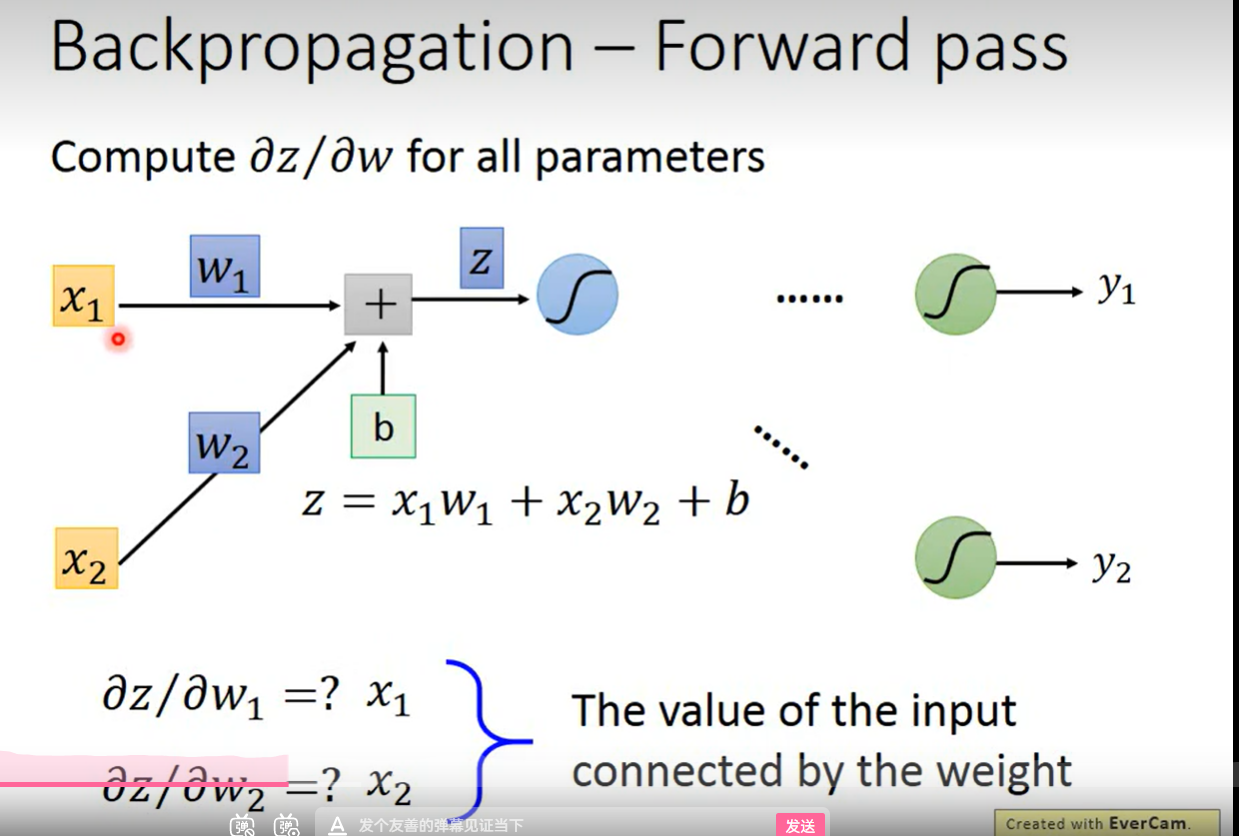
找到规律,对谁的偏微分 ,就等于该输入
反向传播:
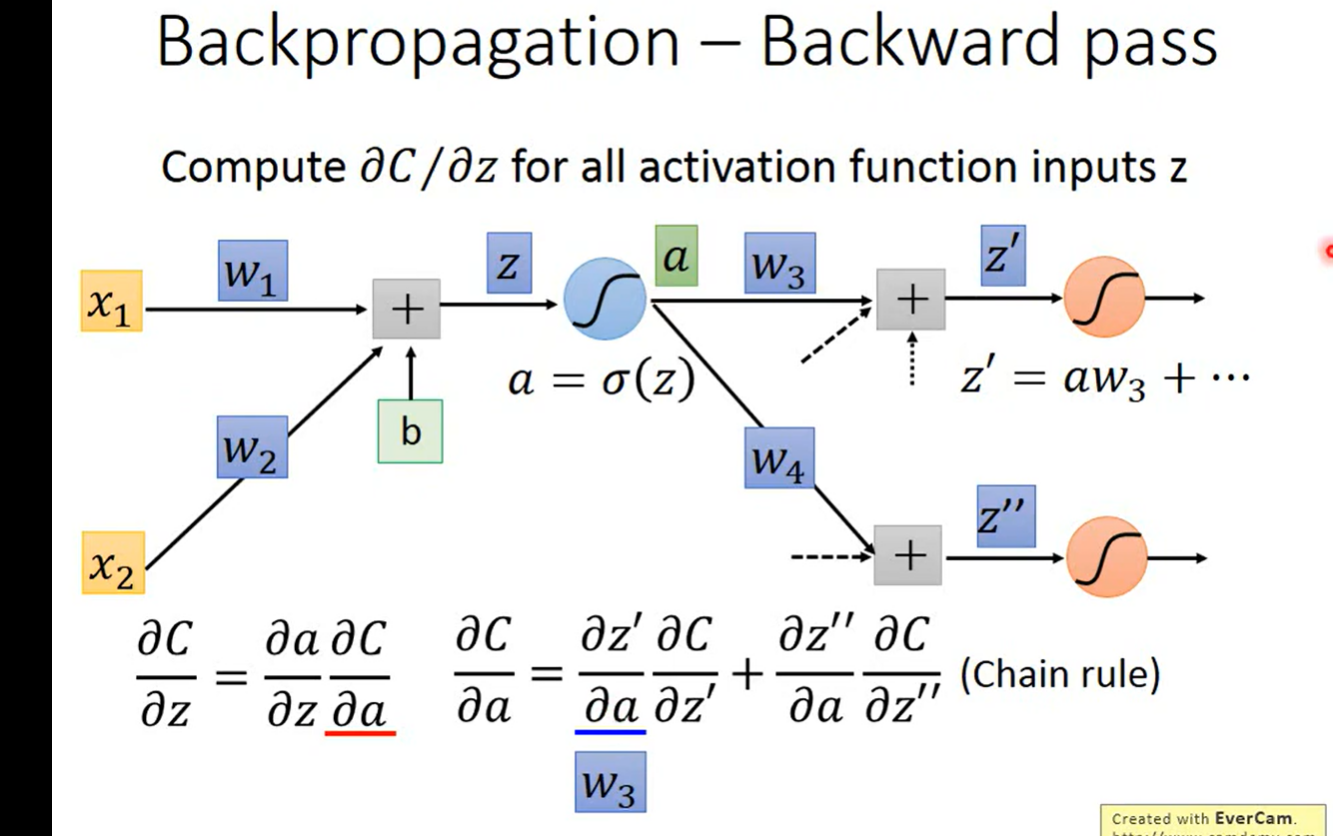
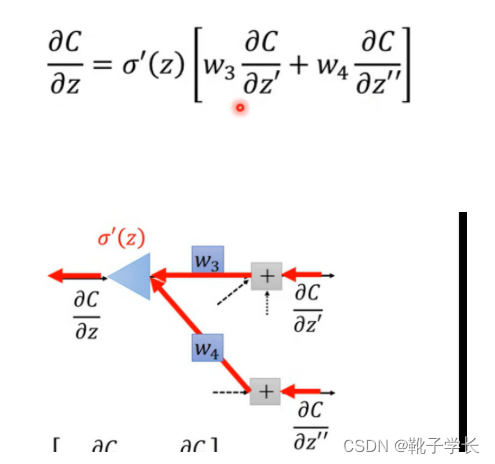
老师这里说 sigmoid ‘(z )是一个常数, 因为z在决定 前馈的 时候就已经决定好了;提问, 为什么?如何理解这个已经决定好了?
如果是按照常数的理解方法的话, z’ 又从何谈起呢?
…… 这个暂时学不进去了
Day6 BackPropagation(2)
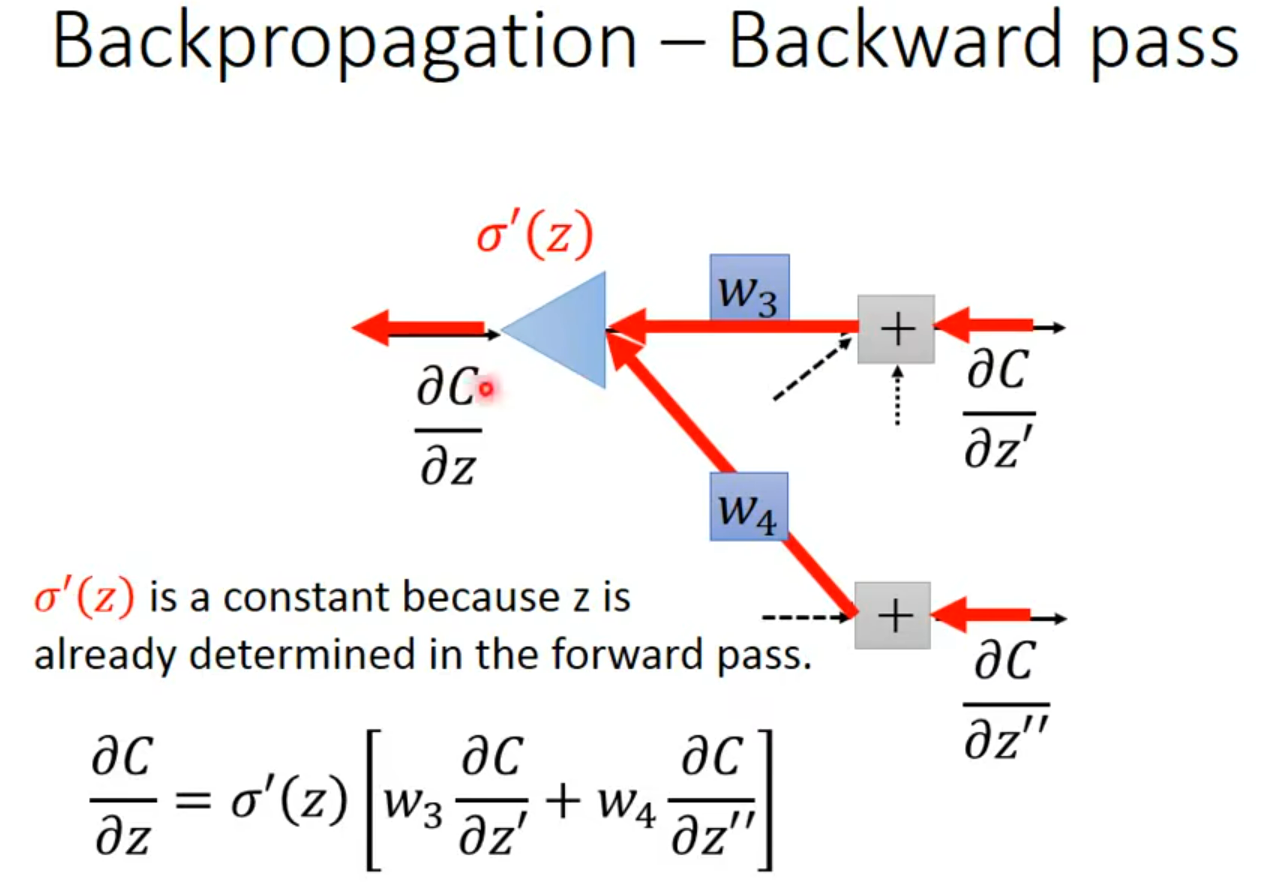
用手推导了一遍具体数字的题目,对反向传播有了更深的理解: 本质上就是梯度下降法;没有丝毫新奇之处;只在于 在深度学习中, L(g(h(……w))),然后我们无法直接求出 L对w 的微分, 需要经过chain rule来进行,这个过程就是反向传播;
至于老师这里说的 sigmoid ‘(z )是一个常数;是因为 z 在前面的前馈中已经计算出来了,就等于输入值和w的线性相加,所以带入以后是一个常数;其实老师讲的很清楚了,是自己对过程不太清晰,把自己绕进去了。
两个case:
case1 . output layer
直接求即可
case2 . hiden layer(not output Layer)
我猜测还是和之前的一样,直到变成case1 为止
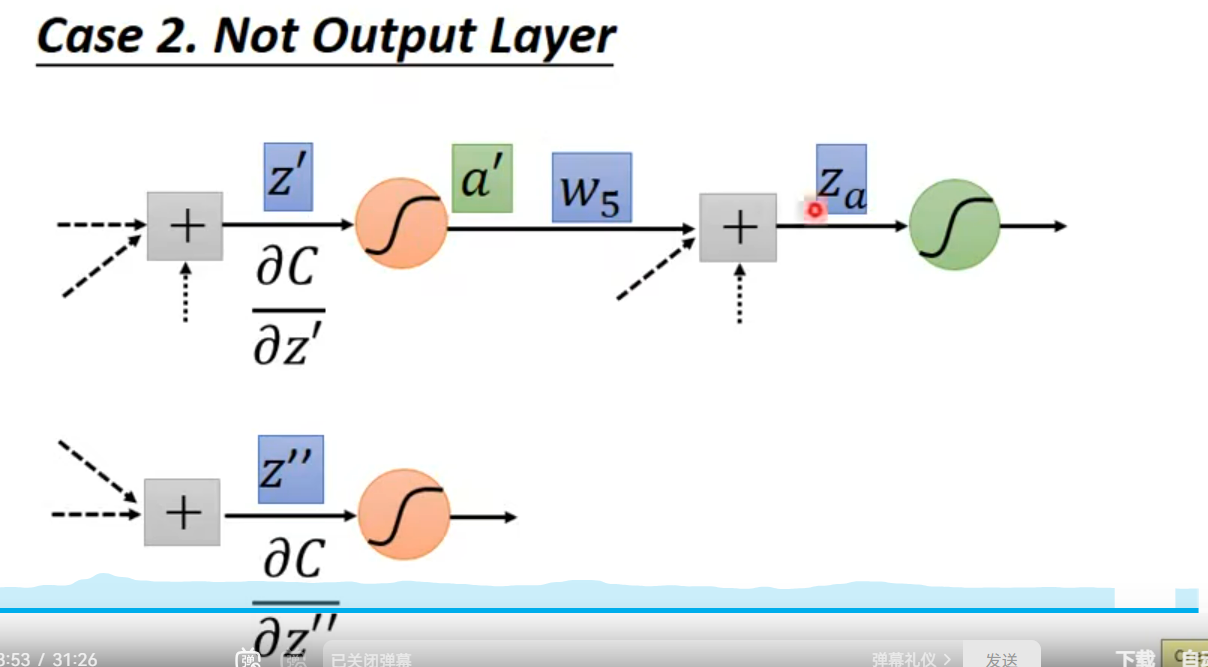
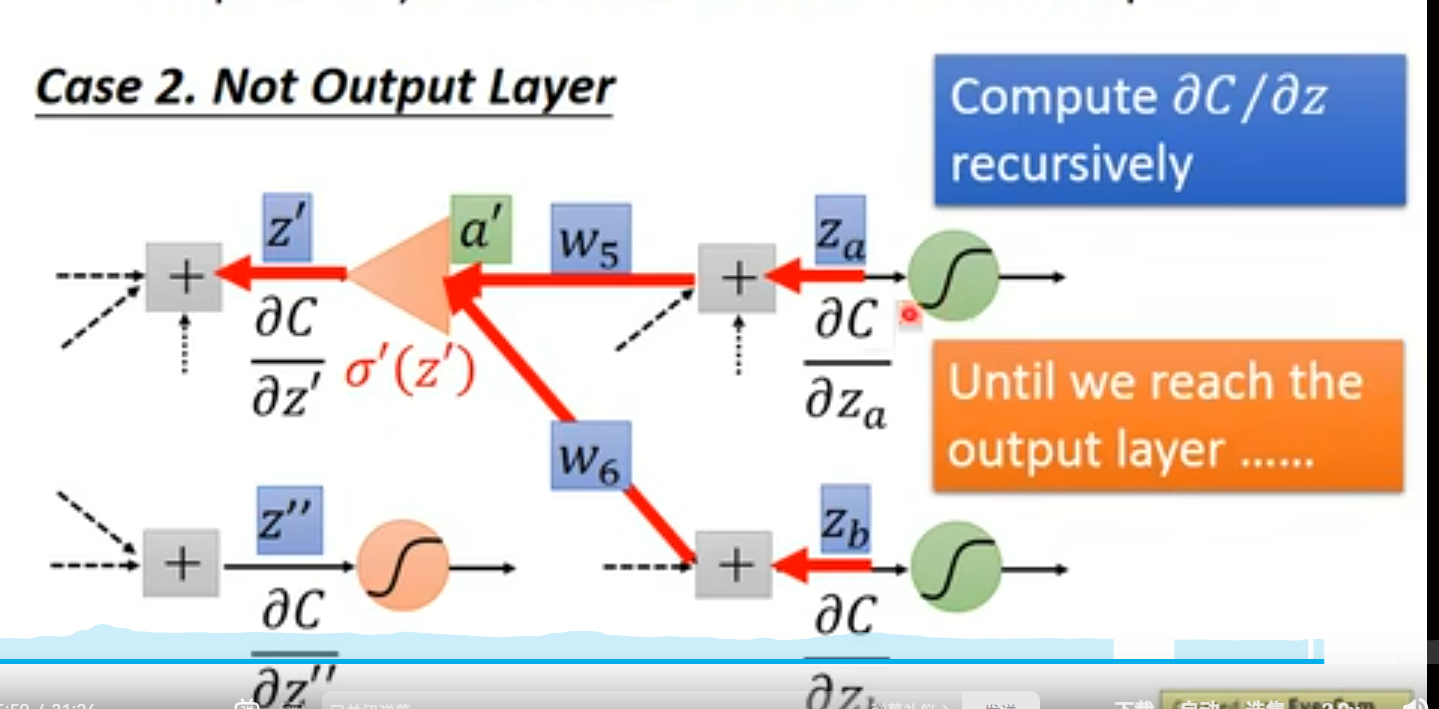
ok 我猜对了~嘿嘿
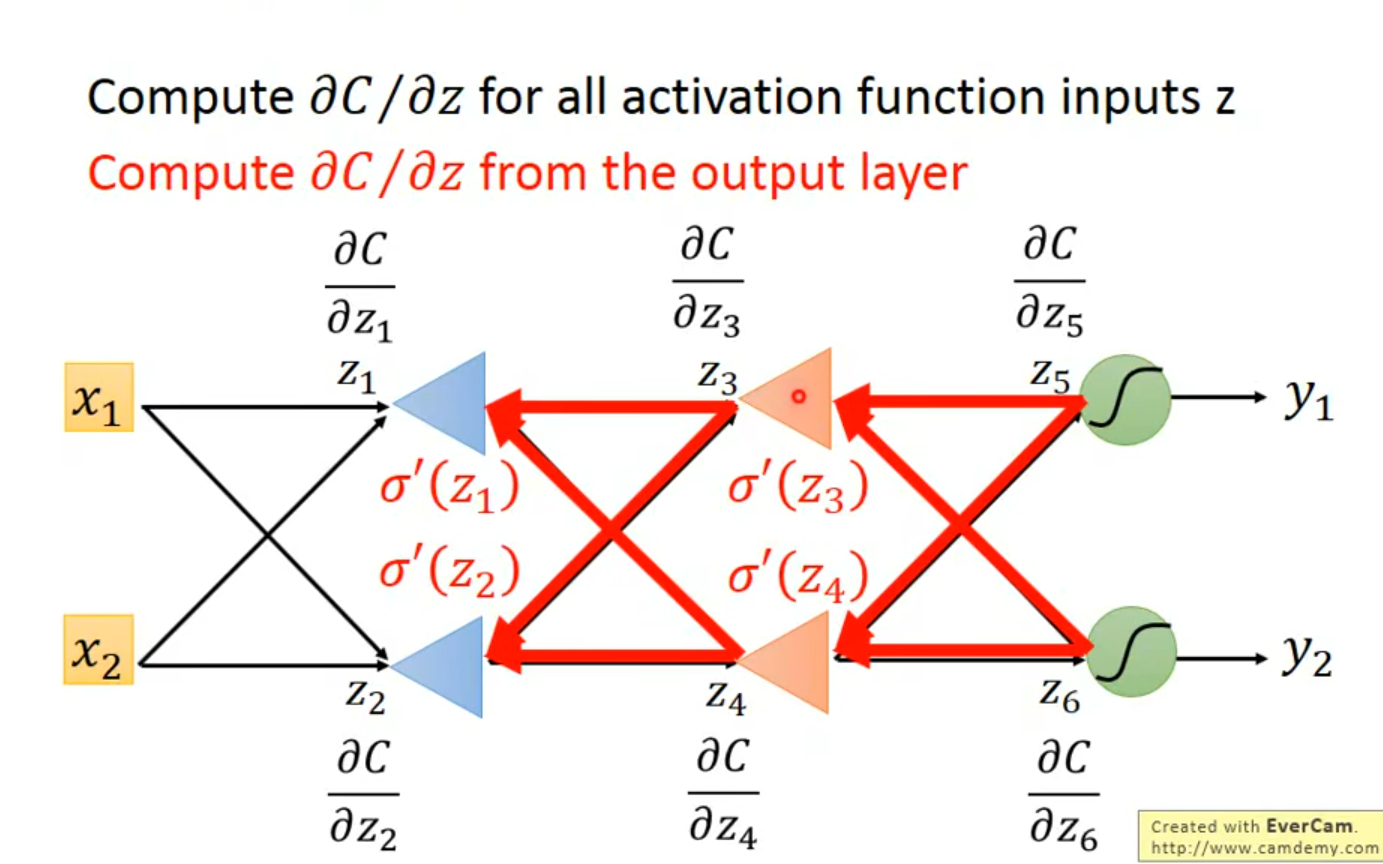
ok 小结一下,反向传播的意义在于减少运算~ 与其正向的求不出来算好几遍 对输出层的偏微分, 不如最开始就直接算 输出层的偏微分
但是扩大的倍率(图中的三角形)需要前一次的正向传播才能求出
相关文章:

机器学习和深度学习 -- 李宏毅(笔记与个人理解1-6)
机器学习和深度学习教程 – 李宏毅(笔记与个人理解) day1 课程内容 什么是机器学习 找函数关键技术(深度学习) 函数 – 类神经网络来表示 ;输入输出可以是 向量或者矩阵等如何找到函数: supervised Lear…...

低功耗全极霍尔开关芯片 D02,磁性开关点精确,对工艺和温度变化不敏感
1、概述 D02 是一款低功耗全极霍尔开关,用于检测施加的磁通量密度,并提供一个数字输出,该输出指示所感测磁通量幅度的当前状态。这些应用的一个例子是翻盖手机中的 ON/OFF 开关。微功耗设计特别适合电池供电系统,如手机或笔记本电…...

初识--数据结构
什么是数据结构?我们为什么要学习数据结构呢....一系列的问题就促使我们不得不了解数据结构。我们不禁要问了,学习C语言不就够了吗?为什么还要学习数据结构呢?这是因为:数据结构能够解决C语言解决不了的问题࿰…...
人工智能前沿成科技竞争新高地
以下文章来源:经济参考报 近日,首届中国具身智能大会(CEAI 2024)在上海举行。作为人工智能领域的前沿热点,具身智能正逐步走进现实,成为当前全球科技竞争的新高地、未来产业的新赛道、经济发展的新引擎。 “…...

【算法刷题day23】Leetcode:669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树
文章目录 Leetcode 669. 修剪二叉搜索树解题思路代码总结 Leetcode 108. 将有序数组转换为二叉搜索树解题思路代码总结 Leetcode 538. 把二叉搜索树转换为累加树解题思路代码总结 草稿图网站 java的Deque Leetcode 669. 修剪二叉搜索树 题目:669. 修剪二叉搜索树 解…...

设计一个会议管理系统100问?
会议管理系统的基本功能有哪些?如何确保会议管理系统的安全性?会议管理系统可以支持多少种不同类型的会议?是否有权限管理功能?是否支持会议室预订功能?会议管理系统可以导入外部参与者信息吗?是否支持多种…...
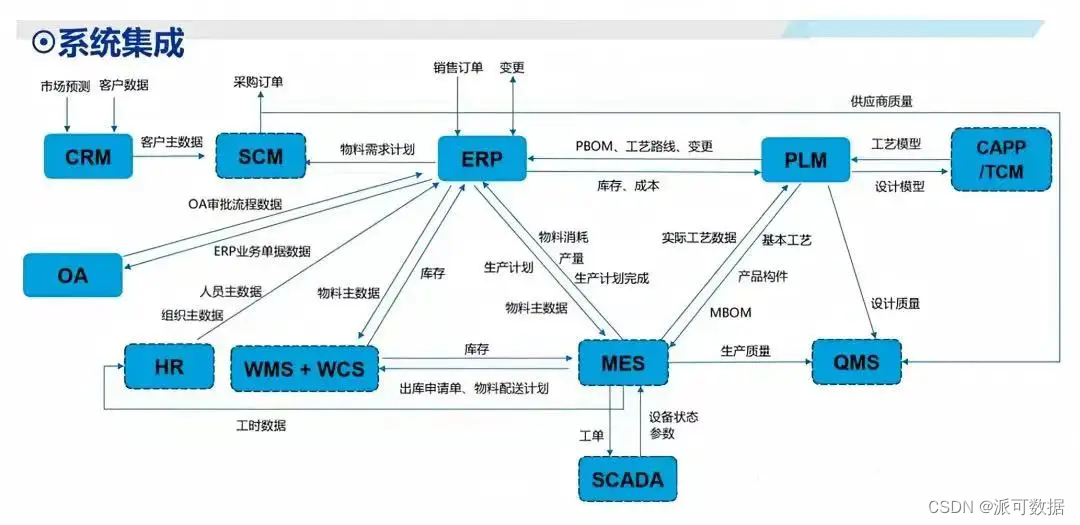
一文搞懂BI、ERP、MES、SCM、PLM、CRM、WMS、APS、SCADA、QMS
在企业信息化数字化过程中我们经常遇到很多系统,比如:MES、ERP、SCM、WMS、APS、SCADA、PLM、QMS、CRM、EAM、BI,这些都是什么系统?有什么功能和作用?它们之间的关系是怎样的? 今天就一文简单分享。 术语 …...
)
全量知识系统 程序详细设计 之 先验逻辑-实现:从“平凡”回到“平凡” (QA 百度搜索)
Q1. 思考:数学中的平凡,和程序中的平凡(比如POJO)、语言中的平凡(比如纯文本),数据中的平凡(比如 Number)。因为我设计中的全知系统将设计的三个方面刻画为语言设计、程序…...
注解(Annotation) --java学习笔记
注解 就是Java代码里的特殊标记,比如:Override、Test等,作用是:让其他程序根据注解信息来决定怎么执行该程序注意:注解可以用在类上、构造器上、方法上、成员变量上、参数上、等位置处 自定义注解 就是自己定义注解 自定义注解到底该怎么写:…...
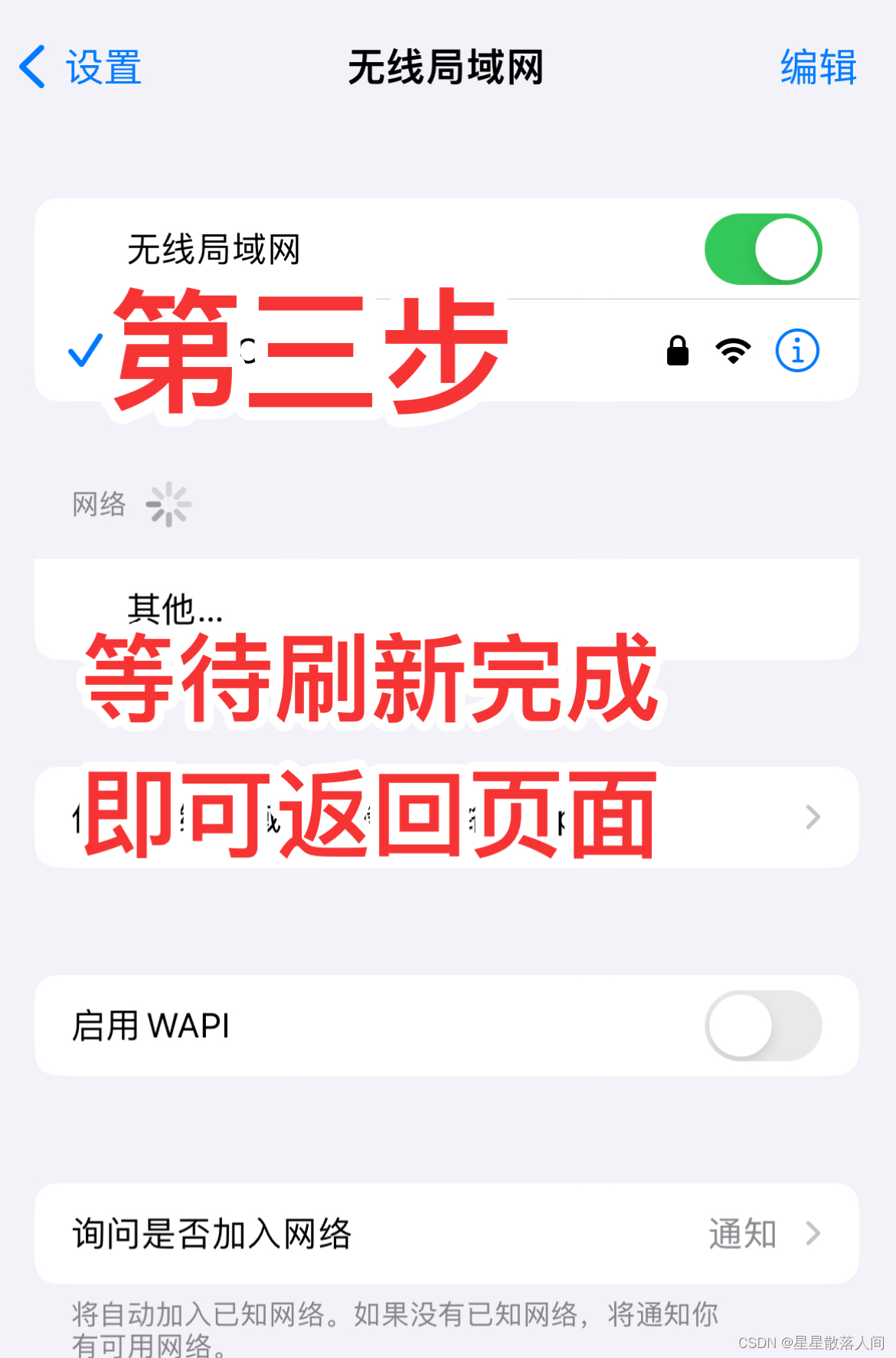
uniapp 小程序获取WiFi列表
<template><view ><button click"getWifiList">获取WiFi列表</button><scroll-view:scroll-top"scrollTop"scroll-yclass"content-pop"><viewclass"itemInfo"v-for"(item, index) in wifiList&…...

数据可视化-ECharts Html项目实战(11)
在之前的文章中,我们学习了如何在ECharts中特殊图表的双y图以及自定义形状词云图。想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错,请留下你宝贵的点赞,谢谢。 数据可视化-ECh…...

【MySQL数据库 | 第二十四篇】Limit语句的性能问题和调优策略
前言: MySQL作为最流行的关系型数据库管理系统之一,被广泛应用于各种规模和类型的应用程序中。其强大的功能和灵活的查询语言使得开发人员能够高效地执行各种数据操作和分析。 然而,在处理大量数据或复杂查询时,一些开发人员可能…...

【数据结构】两两交换链表 复制带随机指针的链表
问题描述1 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 求解 使用一个栈S来存储相邻两个节点即可 /*** Definition for…...
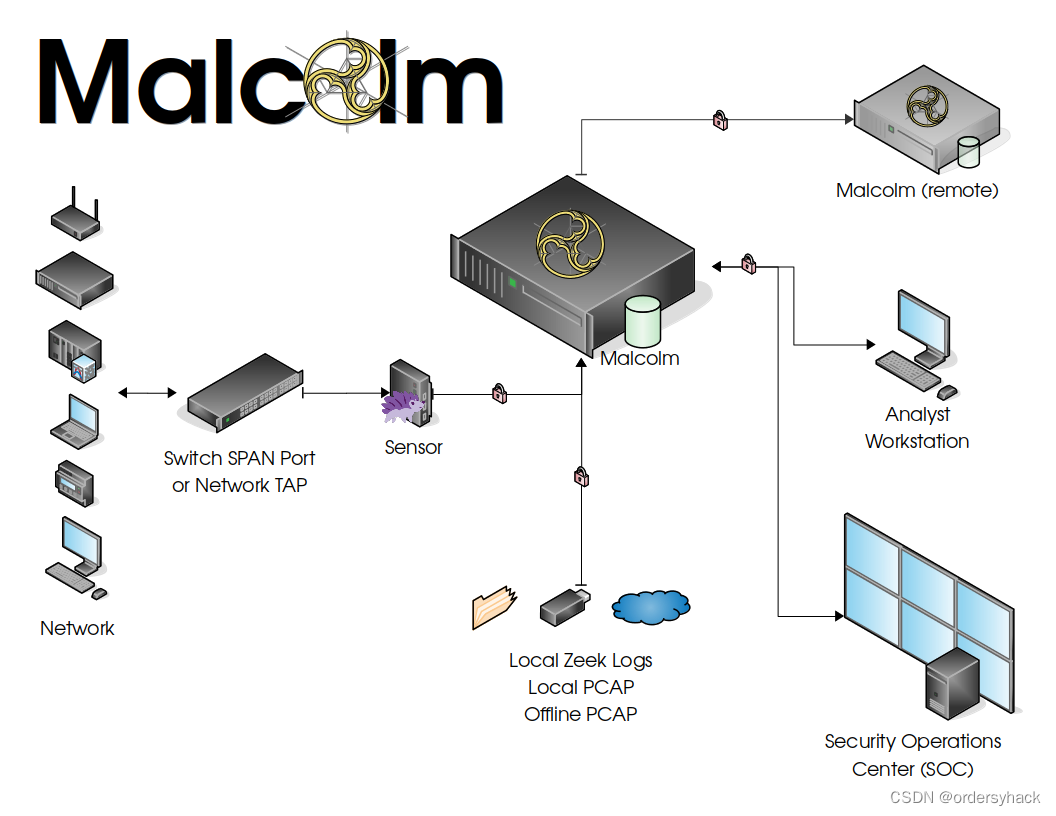
网络安全流量平台_优缺点分析
FlowShadow(流影),Ntm(派网),Elastiflow。 Arkimesuricata,QNSMsuricata,Malcolm套件。 Malcolm套件优点:支持文件还原反病毒引擎(clamav/yara)…...

【c语言】自定义类型:结构体详解
目录 自定义类型:结构体 结构体类型的声明 结构体变量的创建和初始化 结构的特殊声明 结构的自引用 结构体内存对齐 对其规则 为什么存在内存对齐? 修改默认对⻬数 结构体传参 结构体实现位段 位段的内存分配 位段的跨平台问题 位段的应用…...

利用AbortController,取消正在发送的请求
参考文章:https://blog.csdn.net/qq_45560350/article/details/130588101 解决问题:再图层中点击仓库的时候,点击后又取消掉,我们希望这个请求可以被取消掉,我们口可以利用AbortController控制器对象 实操:…...

dockerhub右键快速搜索脚本
Chrome 浏览器扩展的后台脚本,用于创建右键菜单项,并根据用户的操作在新的标签页中打开 Docker Hub 网站或者进行搜索。 // 创建右键菜单项,用于打开 Docker Hub 网站 chrome.contextMenus.create({id: search-home, // 菜单项的唯一标识符t…...
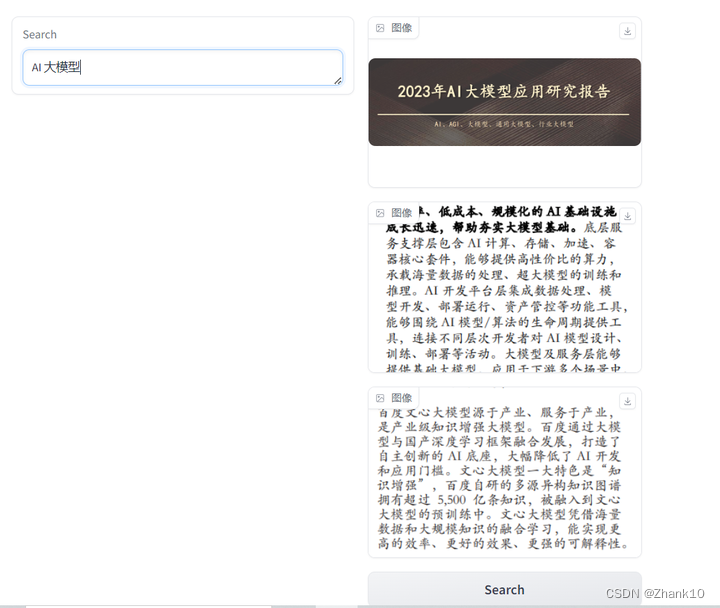
类似微信的以文搜图功能实现
通过PaddleOCR识别图片中的文字,将识别结果报存到es中,利用es查询语句返回结果图片。 技术逻辑 PaddleOCR部署、es部署创建mapping将PaddleOCR识别结果保存至es通过查询,返回结果 前期准备 PaddleOCR、es部署请参考https://blog.csdn.net…...

Android 13.0 Launcher3定制化之最近任务的全部清除由左边移到下边显示
1.概述 在最近13.0的系统rom产品开发中,在Launcher3的定制化开发中,在最近任务列表中,发现点击recents最近任务键后 显示的全部清除按键在左边 由于是横屏的产品显示在左边不太合理 所以要求显示在下边比较合理,所以要从Launcher3的显示流程来解决这个问题 2. 最近任务全…...

成都数字产业园落地全生命周期服务方案, 让企业对成都发展更有信心
国际数字影像产业园,作为现代科技与文化创意的交汇点,致力于为企业落地全生命周期的服务方案,让企业对成都发展更有信心。该服务模式贯穿了企业的初创期到成熟期的各个阶段,确保每一家入驻园区的企业都能得到全方位的支持和帮助。…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...