代码随想录算法训练营第46天|139.单词拆分、多重背包问题
139.单词拆分
题目链接:单词拆分
题目描述:给你一个字符串
s和一个字符串列表wordDict作为字典。如果可以利用字典中出现的一个或多个单词拼接出s则返回true。**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
解题思路:
动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[i]:表示字符串 s前i个字符组成的字符串 s[0…i−1]是否能被拆分成若干个字典中出现的单词 -
确定递推公式
每次转移的时候我们需要枚举包含位置i-1的最后一个单词,看它是否出现在字典中以及除去这部分的字符串是否合法即可。使用变量j遍历分割长度为i的字符串,如果字符串[0……j-1]能被字典中的单词拆分并且字符串[j……i-1]在字典中则dp[i]为true。dp[i]=dp[j] && check(s[j…i−1])
-
dp数组如何初始化
dp[0]=true 表示空串且合法。 -
确定遍历顺序
先遍历字符串i,再遍历子串在字符串中的终止位置j。
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> dict(wordDict.begin(), wordDict.end());vector<bool> dp(s.size() + 1, false);dp[0] = true;for (int j = 0; j <= s.size(); j++) {for (int i = 0; i < j; i++) {string str = s.substr(i, j - i);if (dict.find(str) != dict.end() && dp[i] == true)dp[j] = true;}}return dp[s.size()];}
};
多重背包问题
题目描述:有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量,且价值总和最大。
解题思想:
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
例如:背包最大重量为10。
物品为:
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
问背包能背的物品最大价值是多少?
和如下情况有区别么?
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
毫无区别,这就转成了一个01背包问题了,且每个物品只用一次。
#include <iostream>
#include <vector>using namespace std;
int main(int argc, char *argv[]) {int bagWeight, n;cin >> bagWeight>>n;vector<int> weights(n),values(n),nums(n);int x;for (int i = 0; i < n; i++) cin>>weights[i];for (int i = 0; i < n; i++) cin>>values[i]; for (int i = 0; i < n; i++) cin>>nums[i];for (int i = 0; i < n; i++){int num = nums[i];num--;while(num--){weights.push_back(weights[i]);values.push_back(values[i]);}}vector<int> dp(bagWeight+1,0);for (int i = 0; i < weights.size(); i++){for (int j = bagWeight; j>=weights[i];j--){dp[j] = max(dp[j],dp[j-weights[i]]+values[i]);}}cout << dp[bagWeight];}
这里也有另一种实现方式,就是把每种商品遍历的个数放在01背包里面在遍历一遍。
#include <iostream>
#include <vector>using namespace std;
int main(int argc, char *argv[]) {int bagWeight, n;cin >> bagWeight>>n;vector<int> weights(n),values(n),nums(n);int x;for (int i = 0; i < n; i++) cin>>weights[i];for (int i = 0; i < n; i++) cin>>values[i]; for (int i = 0; i < n; i++) cin>>nums[i];vector<int> dp(bagWeight+1,0);for (int i = 0; i < weights.size(); i++){for (int j = bagWeight; j>=weights[i];j--){for (int k = 1; k <= nums[i] && (j - k * weights[i]) >= 0; k++)dp[j] = max(dp[j],dp[j-weights[i]*k]+values[i]*k);}}cout << dp[bagWeight];return 0;
}
相关文章:

代码随想录算法训练营第46天|139.单词拆分、多重背包问题
139.单词拆分 题目链接:单词拆分 题目描述:给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。 **注意:**不要求字典中出现的单词全部都使用,并且字典中的单词…...
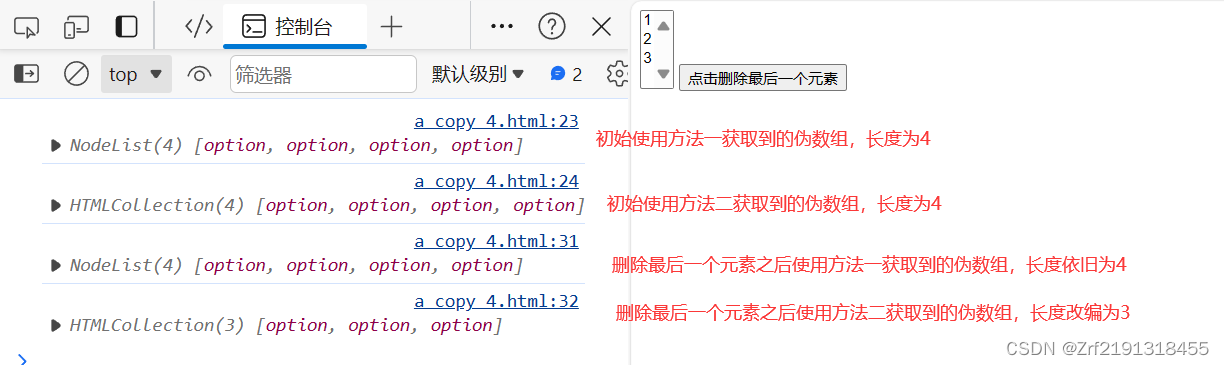
数组与伪数组的区别
大家都知道,在js中使用 document.querySelectorAll(选择器)获取到的为该选择器能选择到的所有元素组成的伪数组,所谓伪数组,就是外表和数组一样,能够使用索引遍历,但本质是对象。 数组与伪数组之间的区别&…...

Java集合List
List特有方法 经典多态写法 // 经典的多态写法 List<String> list new ArrayList<>();常用API:增删改查 // 添加元素 list.add("Java"); // 添加元素到指定位置 list.add(0, "Python");// 获取元素 String s list.get(0);// 修改…...

elasticsearch基础命令
1 字段分词分析: GET /store_info_data/_analyze {"field": "storeName","text":"20pilapala0" }2 精确查找,去除评分 GET /store_info_data/_search {"query": {"constant_score": {"filter": {&quo…...

Capture One 23 Enterprise for Mac中文版 全面的图像处理工具
Capture One 23 Enterprise for Mac中文版一款专业的图像编辑和管理软件,具备强大的功能和工具,适用于摄影师、摄影工作室和专业用户。 软件下载:Capture One 23 Enterprise for Mac中文版下载 该软件为用户提供了全面的图像处理工具…...
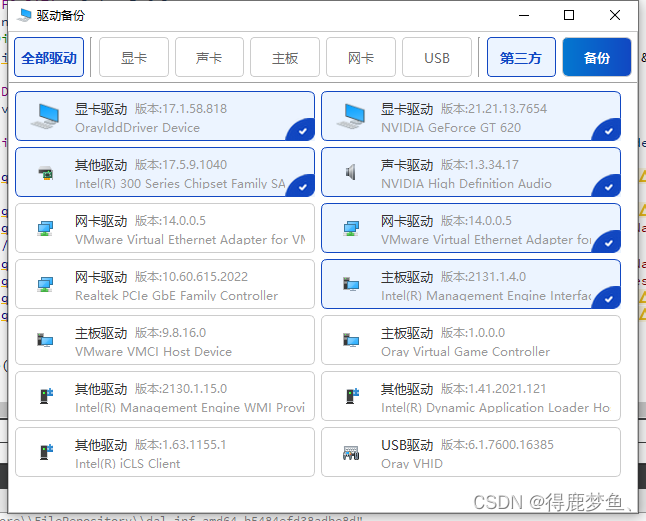
Qt案例 通过调用Setupapi.h库实现对设备管理器中设备默认驱动的备份
参考腾讯电脑管家-软件市场中的驱动备份专家写的一个驱动备份软件案例,学习Setupapi.h库中的函数使用.通过Setupapi.h库读取设备管理器中安装的设备获取安装的驱动列表,通过bit7z库备份驱动目录下的所有文件. 目录导读 实现效果相关内容示例获取SP_DRVIN…...

如何理解JVM
JVM(Java虚拟机)是Java程序的运行环境,它是Java技术的核心组成部分之一。理解JVM涉及到以下几个方面的内容: 1. **虚拟机概念**:虚拟机是一种软件实体,它在物理计算机上模拟出一个计算机系统,使…...

第十四讲:C语言字符函数和字符串函数
目录 1. 字符分类函数 2、字符转换函数 3. strlen的使⽤和模拟实现 4. strcpy 的使⽤和模拟实现 5. strcat 的使⽤和模拟实现 6. strcmp 的使⽤和模拟实现 7. strncpy 函数的使⽤ 8. strncat 函数的使⽤ 9. strncmp函数的使⽤ 10. strstr 的使⽤和模拟实现 11. strt…...

华为海思2024春招数字芯片岗机试题(共9套)
huawei海思2024春招数字芯片岗机试题(共9套,有答案和解析,答案非官方,未仔细校正,仅供参考)(WX:didadidadidida313,加我备注:CSDN huawei数字题目,谢绝白嫖哈)…...

分类预测 | Matlab实现KPCA-IDBO-LSSVM基于核主成分分析和改进蜣螂优化算法优化最小二乘支持向量机分类预测
分类预测 | Matlab实现KPCA-IDBO-LSSVM基于核主成分分析和改进蜣螂优化算法优化最小二乘支持向量机分类预测 目录 分类预测 | Matlab实现KPCA-IDBO-LSSVM基于核主成分分析和改进蜣螂优化算法优化最小二乘支持向量机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述…...

与机器对话:ChatGPT 和 AI 语言模型的奇妙故事
原文:Talking to Machines: The Fascinating Story of ChatGPT and AI Language Models 译者:飞龙 协议:CC BY-NC-SA 4.0 从 ELIZA 到 ChatGPT:会话式人工智能的简史 会话式人工智能是人工智能(AI)的一个分…...

概率论基础——拉格朗日乘数法
概率论基础——拉格朗日乘数法 概率论是机器学习和优化领域的重要基础之一,而拉格朗日乘数法与KKT条件是解决优化问题中约束条件的重要工具。本文将简单介绍拉格朗日乘数法的基本概念、应用以及如何用Python实现算法。 1. 基本概念 拉格朗日乘数法是一种用来求解…...

[xboard]real6410-6.2 移植kernel网络驱动
文章目录 硬件电路软件配置问题1问题2问题3问题4功能测试硬件电路 核心板,使用DM9000A [图片] 软件配置 问题1 / # / # ifconfig ifconfig: /proc/net/dev: No such file or directory ifconfig: socket: Fun...

Quarkus初探
Quarkus初探 背景安装Quarkus安装Quarkus CLI 创建Quarkus项目运行Quarkus初探代码修改一下代码 数据持久化创建PanacheEntiry写入数据读取数据 Dev Service使用外部数据库区分dev和prod 构建native应用(依赖Graalvm) 背景 最早是在Infoq上了解到Quarku…...

90天玩转Python-02-基础知识篇:初识Python与PyCharm
90天玩转Python系列文章目录 90天玩转Python—01—基础知识篇:C站最全Python标准库总结 90天玩转Python--02--基础知识篇:初识Python与PyCharm 90天玩转Python—03—基础知识篇:Python和PyCharm(语言特点、学习方法、工具安装&…...
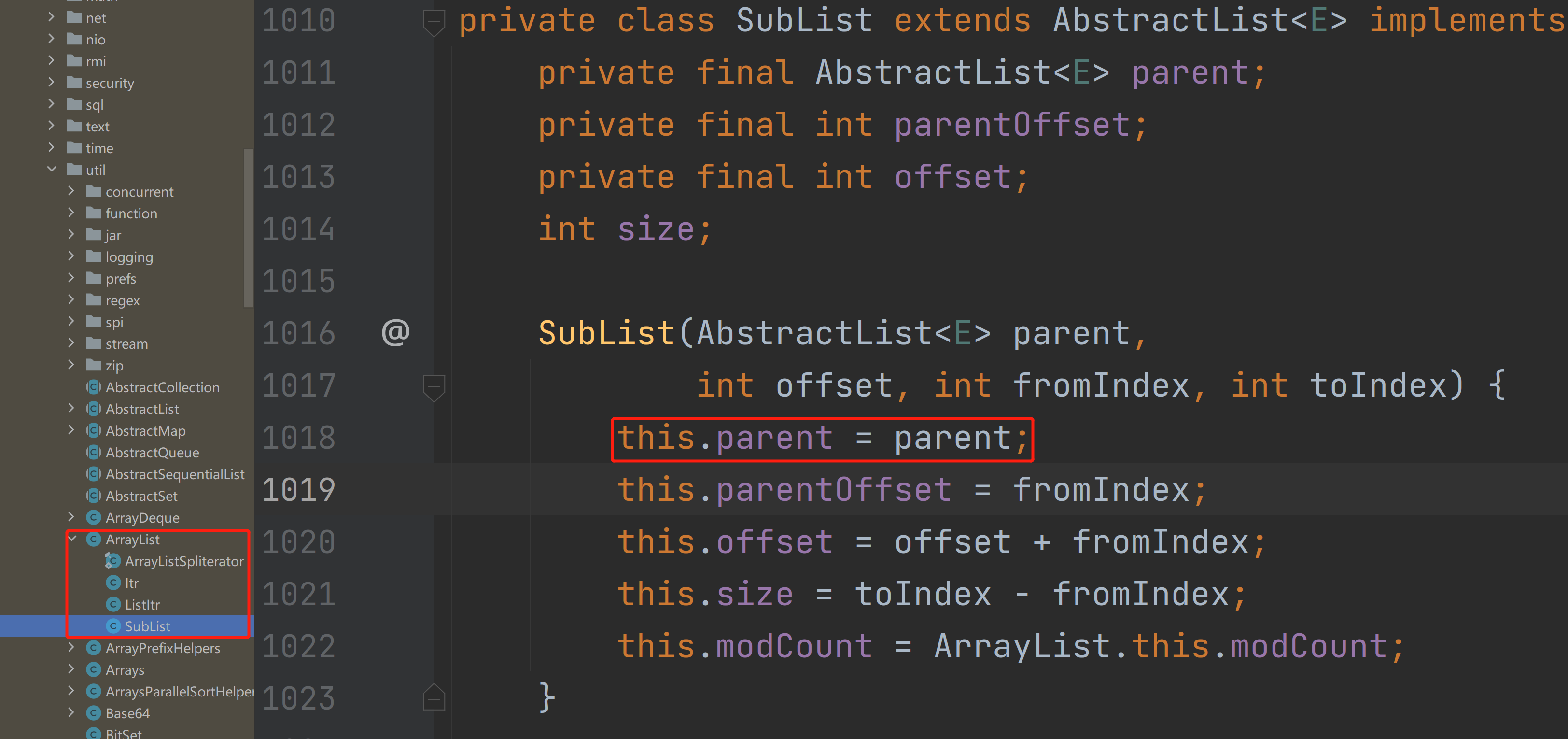
List操作的一些常见问题
1. Arrays.asList转换基本类型数组 在实际的业务开发中,我们通常会进行数组转List的操作,通常我们会使用Arrays.asList来进行转换,但是在转换基本类型的数组的时候,却出现转换的结果和我们想象的不一致。 import java.util.Arra…...

如何使用Java和RabbitMQ实现延迟队列?
前言 今天我们使用Java和RabbitMQ实现消息队列的延迟功能。 前期准备,需要安装好docker、docker-compose的运行环境。 需要安装RabbitMQ的可以看下面这篇文章。 如何使用PHP和RabbitMQ实现消息队列?-CSDN博客 今天讲的是依赖RabbitMQ的延迟插件实现…...

AI论文速读 | TF-LLM:基于大语言模型可解释性的交通预测
论文标题: Explainable Traffic Flow Prediction with Large Language Models 作者:Xusen Guo, Qiming Zhang, Mingxing Peng, Meixin Zhu(朱美新)*, Hao (Frank)Yang(杨昊) 机构:香港科技大学(广州),约翰…...

智慧矿山视频智能监控与安全监管方案
一、行业背景 随着全球能源需求的日益增长,矿业行业作为国民经济的重要支柱,其发展日益受到广泛关注。然而,传统矿山管理模式的局限性逐渐显现,如生产安全、人员监管、风险预警等方面的问题日益突出。因此,智慧矿山智…...
2024春算法训练4——函数与递归题解
一、前言 感觉这次的题目都很好,但是E题....(我太菜了想不到),别人的题解都上百行了,晕; 二、题解 A-[NOIP2010]数字统计_2024春算法训练4——函数与递归 (nowcoder.com) 这种题目有两种做法:…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
