第十届蓝桥杯大赛个人赛省赛(软件类) CC++ 研究生组2.0
A立方和
#include<iostream>
#include<cmath>
using namespace std;
int main(){int n, t, flag, x;long long ans = 0;for(int i = 1; i <= 2019; i++){t = i;flag = 0;while(t && !flag){x = t % 10;if(x == 2 || x == 0 || x == 1 || x == 9) flag = 1;t /= 10;}if(flag) ans += (long long)pow(i, 3);}printf("%lld", ans);//4097482414389return 0;
}
打卡题
B字串数字
#include<iostream>
#include<string>
using namespace std;
int main(){string s = "LANQIAO";
// string s = "LQ";long long power = 1, ans = 0;for(int i = s.size() - 1; i >= 0; i--){ans += (s[i] - 'A' + 1) * power;power *= 26;}printf("%lld", ans);//3725573269return 0;
}
进制转换
C质数
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
bool isPrime(ll n){ll sqr = sqrt(n);for(int i = 2; i <= sqr; i++){if(n % i == 0) return false;}return true;
}
int main(){ll x = 2, cnt = 0, ans;while(cnt < 2019){if(isPrime(x)){cnt++;ans = x;}x++;}printf("%lld", ans);//17569return 0;
}
类似于质数打表
D最短路
6
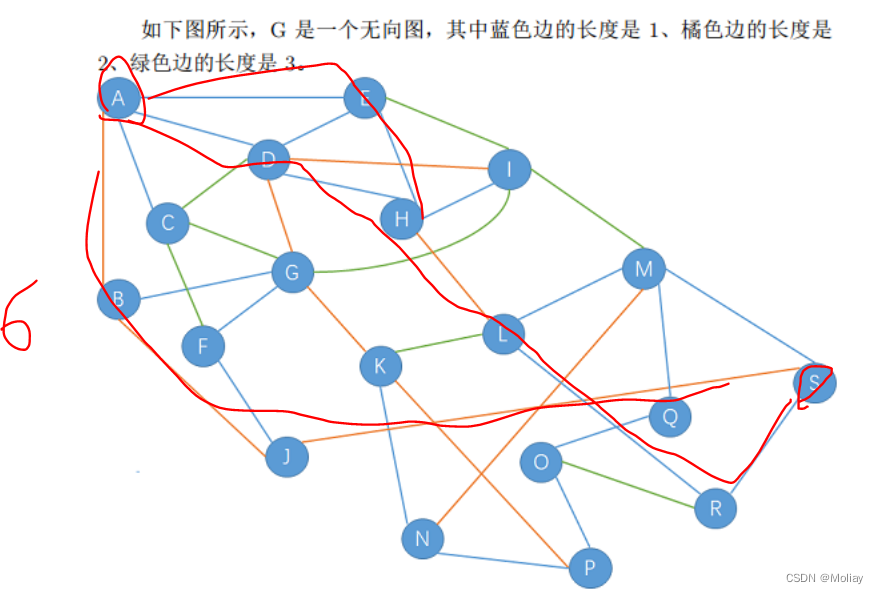
适当手算,灵活些
E RSA解密
没思路
尝试先把p,q试出来
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
int main(){ll n = 1001733993063167141LL, sqr = sqrt(n);for(ll i = 2; i <= sqr; i++){if(n % i == 0){printf("%lld ", i);if(i * i != n) printf("%lld ", n / i);}}return 0;
}
发现de % (p-1)(q-1)=1其实也就是求d的逆元,联想到用扩欧。
解密过程是快速幂的经典应用啦~
#include<iostream>
#include<cmath>
using namespace std;
typedef __int128 ll;ll exGcd(ll a, ll b, ll &x, ll &y){if(b == 0){x = 1;y = 0;return a;}int g = exGcd(b, a % b, x, y), temp = x;x = y;y = temp - a / b * y;return g;
}ll inverse(ll a, ll b){ll x, y;ll g = exGcd(a, b, x, y);if(g == 1) return (x % b + b) % b;else return -1;
}ll fastPow(ll a, ll b, ll m){//计算过程中会有超出long long的情况,故设置为__int128类型 if(b == 0) return 1;else if(b & 1) return a * fastPow(a, b - 1, m) % m;else{ll t = fastPow(a, b / 2, m);return t * t % m;}
}int main(){ll p = 891234941LL, q = 1123984201LL, d = 212353, n = 1001733993063167141LL, e, c = 20190324LL;ll t = (p - 1) * (q - 1);e = inverse(d, t);//de % t = 1 扩欧求d的逆元 printf("%lld", fastPow(c, e, n));//快速幂return 0;
}
F 斐波那契额序列与黄金分割
先打印前一百个观察下数据,发现大于等于19后在保留八位小数的基础上就稳定在一个比值,符合提示的趋近于黄金分割。而且当数值过大时,比值会出现负数的情况,显然异常。考虑可能是因为斐波那契额数列增长速度过快,超出了int型范围。才100就超了,给定的n范围更超,索性利用后续在规定的精度内稳定于一个比值,直接打印不再计算。
#include<iostream>
using namespace std;
typedef long long ll;
int main(){ll f1 = 1, f2 = 1, f, n;for(int i = 3; i <= 100; i++){f = f1 + f2;printf("%d %.8f\n", i - 1, 1.0 * f2 / f);f1 = f2;f2 = f;}return 0;
}
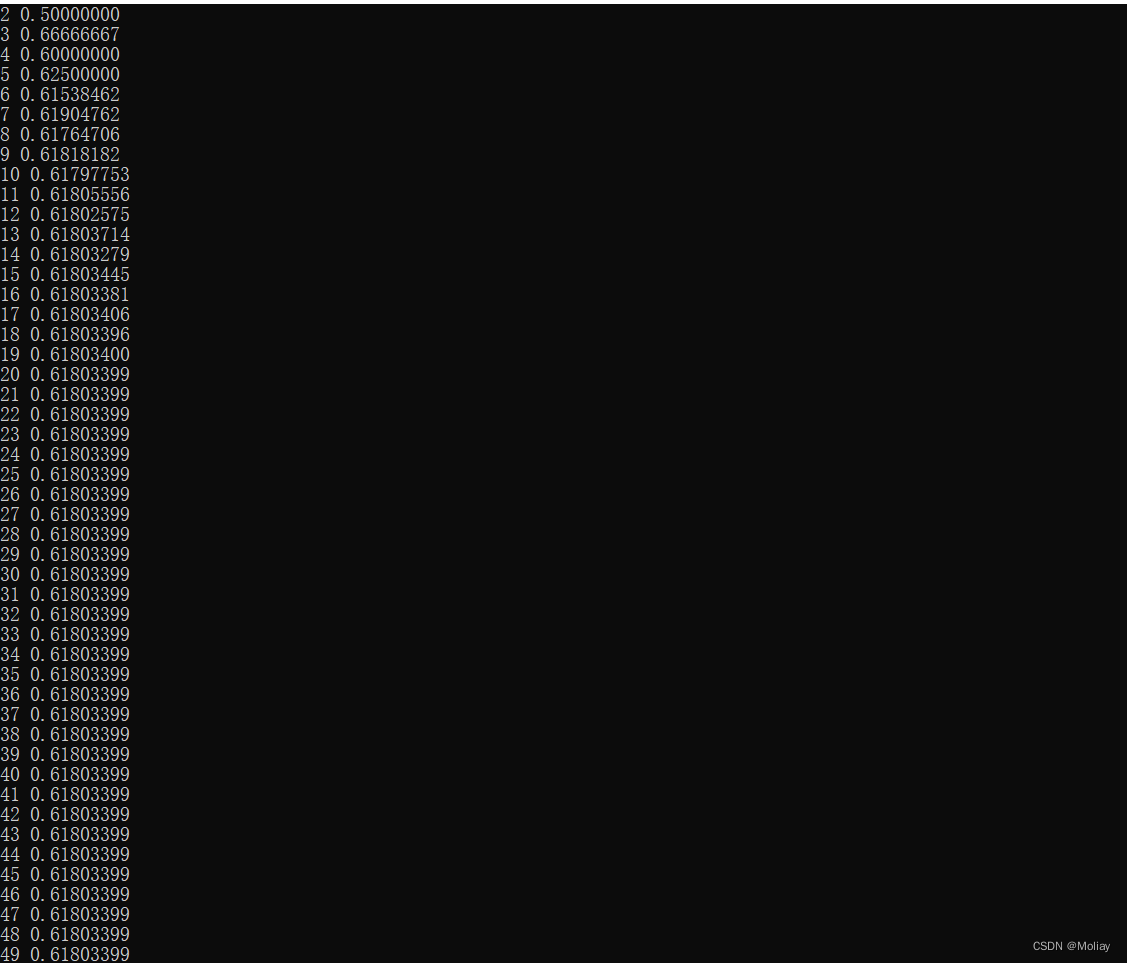
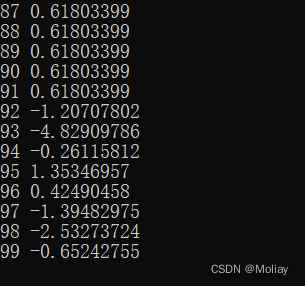
提交程序为
#include<iostream>
using namespace std;
typedef long long ll;
int main(){ll f1 = 1, f2 = 1, f, n;scanf("%lld", &n);if(n > 20) printf("0.61803399");else{for(int i = 3; i <= n + 1; i++){f = f1 + f2;if(i == n + 1)printf("%.8f", 1.0 * f2 / f);f1 = f2;f2 = f;}}return 0;
}
一个测试点没过,忽略了n==2的情况
#include<iostream>
using namespace std;
typedef long long ll;
int main(){ll f1 = 1, f2 = 1, f, n;scanf("%lld", &n);if(n > 20) printf("0.61803399");else{for(int i = 2; i < n + 1; i++){f = f1 + f2;f1 = f2;f2 = f;}printf("%.8f", 1.0 * f1 / f2);}return 0;
}
G扫地机器人
不知道如何下手
走廊长度n为105,根据数据范围需要选择nlogn以内的算法。花费时间最短2,最长2*n,考虑二分处理。
在花费时间t内,判断是否能够扫完n个格子。用贪心,尽量让机器人扫其周围的格子且平均得划分。把机器人的位置升序排序,看机器人在时间t内,能够覆盖的右边界能否相互衔接上且最后一个机器人能够覆盖到走廊有边界。
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 10;
int a[maxn], n, k, l, r, mid;bool judge(int len){int r = 0;//上一个机器人能扫到的右边界for(int i = 0; i < k; i++){if(a[i] - len > r) return false;//不能衔接上,有覆盖不到的区域,则不可行else{if(a[i] < r) r = a[i] + len - 1;//在上一个机器人可覆盖的区域内else r += len;//在边界上 } }return r >= n;
}int main(){scanf("%d%d", &n, &k);for(int i = 0; i < k; i++){scanf("%d", a + i);}sort(a, a + k);l = 0;r = n;while(l < r){mid = (l + r) / 2;if(judge(mid)) r = mid;//当前可行,尝试更短 else l = mid + 1; //当前不可行,增加时间 }printf("%d", 2 * (l - 1)); return 0;
}
H修改数组
#include<iostream>
using namespace std;
const int maxn = 1e5 + 10, maxv = 1e6 + 1e5;
int a[maxn], flag[maxv] = {0};
int main(){int n;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d", a + i);if(!flag[a[i]]) flag[a[i]] = 1;else {a[i] += flag[a[i]];while(flag[a[i]]) a[i]++;flag[a[i]]++;}}for(int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}
两个测试点超时
没有充分利用flag的出现次数,还是一个个的跳且没有正确累加后续的出现次数
#include<iostream>
using namespace std;
const int maxn = 1e5 + 10, maxv = 1e6 + 1e5;
int a[maxn], flag[maxv] = {0};
int main(){int n, t;scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d", a + i);while(flag[a[i]]){t = a[i];a[i] += flag[t];flag[t]++;}flag[a[i]] = 1;}for(int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}
I 灵能传输
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 3e5 + 10;
int a[maxn];
int main(){int t, n, flag, x, p, temp;scanf("%d", &t);while(t--){scanf("%d", &n);for(int i = 0; i < n; i++){scanf("%d", a + i);}flag = 1;while(flag){x = abs(a[0]);p = 0;for(int i = 1; i < n; i++){if(abs(a[i]) > x){x = abs(a[i]);p = i;}}if(x == 0) flag = 1;if(p == 0) p++;else if(p == n - 1) p--;temp = max(max(abs(a[p - 1] + a[p]), abs(a[p + 1] + a[p])), abs(a[p]));if(temp >= x) flag = 0;else{a[p - 1] += a[p];a[p + 1] += a[p];a[p] = -a[p];}}printf("%d\n", x);}return 0;
}
骗了四个测试点的分。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int main(){int n, t;scanf("%d", &t);while(t--){ll x, ansX = 0;scanf("%d", &n);vector<ll> sum(n + 1, 0);vector<ll> visit(n + 1, 0);vector<ll> ans(n + 1, 0); for(int i = 1; i <= n; i++){scanf("%lld", &x);sum[i] = sum[i - 1] + x;}ll l = sum[0], r = sum[n], lp = 0, rp = n, ansL = 0, ansR = n;//首位项的值if(l > r) swap(l, r);sort(sum.begin(), sum.end());for(int i = 0; i < n; i++){if(sum[i] == l){lp = i;break;}}for(int i = 0; i < n; i++){if(sum[i] == r){rp = i;break;}}for(int i = rp; i <= n; i += 2){//填充结果数组 ans[ansR--] = sum[i];visit[i] = 1; }for(int i = lp; i >= 0; i -= 2){ans[ansL++] = sum[i];visit[i] = 1;}for(int i = 0; i <= n; i++){if(!visit[i]) ans[ansL++] = sum[i];}for(int i = 1; i <= n; i++){if(abs(ans[i] - ans[i - 1]) > ansX) ansX = abs(ans[i] - ans[i - 1]);}printf("%lld\n", ansX);}return 0;
}
J空间跳跃
题干看起来好麻烦,蒟蒻不想做了
相关文章:

第十届蓝桥杯大赛个人赛省赛(软件类) CC++ 研究生组2.0
A立方和 #include<iostream> #include<cmath> using namespace std; int main(){int n, t, flag, x;long long ans 0;for(int i 1; i < 2019; i){t i;flag 0;while(t && !flag){x t % 10;if(x 2 || x 0 || x 1 || x 9) flag 1;t / 10;}if(fl…...
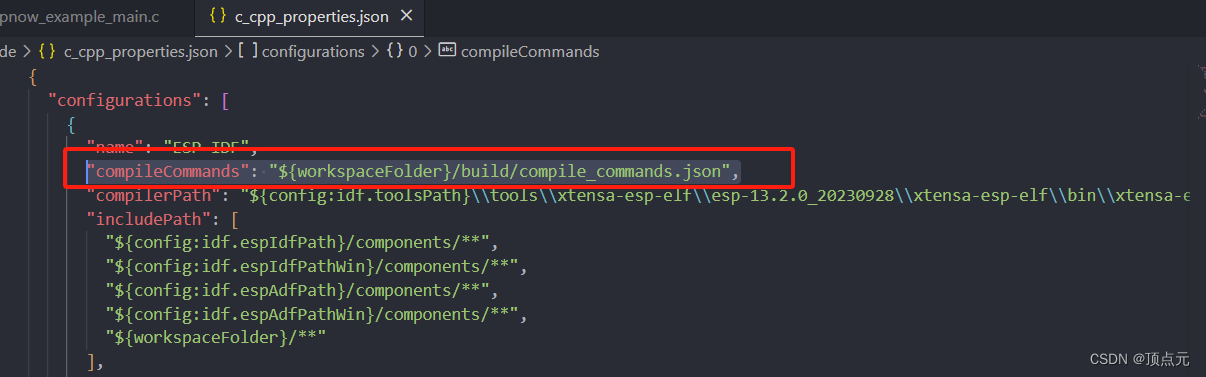
vscode开发ESP32问题记录
vscode 开发ESP32问题记录 1. 解决vscode中的波浪线警告 1. 解决vscode中的波浪线警告 参考链接:https://blog.csdn.net/fucingman/article/details/134404485 首先可以通过vscode 中的IDF插件生成模板工程,这样会自动创建.vscode文件夹中的一些json配…...
R语言复现:轨迹增长模型发表二区文章 | 潜变量模型系列(2)
培训通知 Nhanes数据库数据挖掘,快速发表发文的利器,你来试试吧!欢迎报名郑老师团队统计课程,4.20直播。 案例分享 2022年9月,中国四川大学学者在《Journal of Psychosomatic Research》(二区,I…...

【数据结构】顺序表的实现——动态分配
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:数据结构 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

3.3.k8s搭建-rancher RKE2
目录 RKE2介绍 k8s集群搭建 搭建k8s集群 下载离线包 部署rke2-server 部署rke2-agent 部署helm 部署rancher RKE2介绍 RKE2,也称为 RKE Government,是 Rancher 的下一代 Kubernetes 发行版。 官网地址:Introduction | RKE2 k8s集群搭…...
CST电磁仿真软件的设置变更与问题【官方教程】
保存结果的Result Navigator 积累的结果一目了然! 用户界面上的Result Navigator 在一个仿真工程中更改变量取值进行仿真分析或者改变设置进行仿真分析时,之前的1DResult会不会消失呢? 1D Result:CST中1D Result指的是Y值取决…...
保研线性代数复习3
一.基底(Basis) 1.什么是生成集(Generating Set)?什么是张成空间(Span)? 存在向量空间V(V,,*),和向量集(xi是所说的列向量ÿ…...

从零开始学Spring Boot系列-集成MyBatis-Plus
在Spring Boot应用开发中,MyBatis-Plus是一个强大且易于使用的MyBatis增强工具,它提供了很多实用的功能,如代码生成器、条件构造器、分页插件等,极大地简化了MyBatis的使用和配置。本篇文章将指导大家如何在Spring Boot项目中集成…...

【云原生篇】k8s之Deployment详解
Kubernetes 的 Deployment 是一种管理声明式更新的资源对象,它允许你描述应用的期望状态,并由 Deployment 控制器自动将当前状态改变为期望状态。Deployment 主要用于无状态应用的部署和扩展,但也可以用于有状态应用。 核心功能 自动化部署…...
linux安装dubboAdmin
1.环境准备: jdk-8u391-linux-x64apache-maven-3.9.6apache-tomcat-8.5.100 2.安装注册中心zookeeper zookeeper的安装看我的另一篇文章,安装完成后保持启动状态 linux安装Zookeeper的详细步骤-CSDN博客 3.安装dubboadmin 源码下载地址:R…...

Android 系统编译 and 应用裁剪
平台应用编译 平台应用demo的Android.mk写法: LOCAL_PATH:= $(call my-dir) include $(CLEAR_VARS)LOCAL_MODULE_TAGS := optional# Only compile source java files in this apk. LOCAL_SRC_FILES := $(call all-java-files-under, src)LOCAL_PACKAGE_NAME := TestLOCAL_CER…...
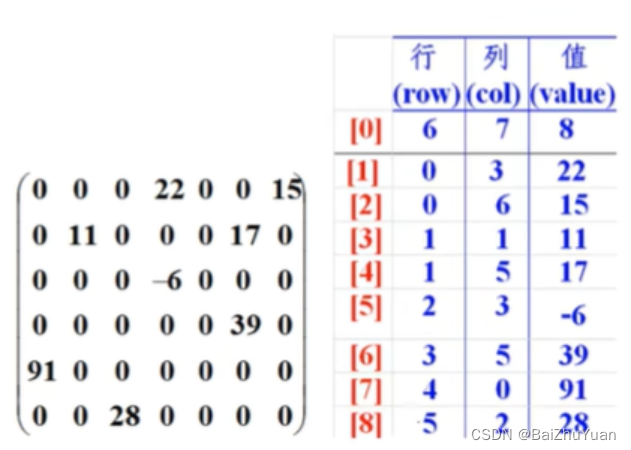
java数组.day16(冒泡排序,稀疏数组)
冒泡排序 冒泡排序无疑是最为出名的排序算法之一,总共有八大排序! 冒泡的代码还是相当简单的,两层循环,外层冒泡轮数,里层依次比较,江湖中人人尽皆知。 我们看到嵌套循环,应该立马就可以得出这个算法的时…...
vue+springboot多角色登录
①前端编写 将Homeview修改为manager Manager: <template><div><el-container><!-- 侧边栏 --><el-aside :width"asideWidth" style"min-height: 100vh; background-color: #001529"><div style"h…...

使用 ADB 查找应用名称和活动名称,并启动指定页面
知识点和难题: 查找应用名称和活动名称: 使用 ADB 命令 adb shell dumpsys window | findstr mCurrentFocus 可以查找当前设备上活动的应用名称和活动名称。 保存输出结果: 将命令的输出结果保存到文件中,方便后续使用。 启动指…...

LangChain - 文档转换
文章目录 一、文档转换器 & 文本拆分器文本拆分器 二、开始使用文本拆分器三、按字符进行拆分四、代码分割 (Split code)1、PythonTextSplitter2、JS3、Markdown4、Latex5、HTML6、Solidity 五、MarkdownHeaderTextSplitter1、动机2、Use case 六、递归按字符分割七、按tok…...

【C++】STL--list
目录 list的介绍 list的使用 list的构造 list iterator的使用 list capacity list modifiers list的迭代器失效 list模拟实现 list的介绍 1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向…...

二. CUDA编程入门-双线性插值计算
目录 前言0. 简述1. 执行一下我们的第十个CUDA程序2. Bilinear interpolation3. 代码分析总结参考 前言 自动驾驶之心推出的 《CUDA与TensorRT部署实战课程》,链接。记录下个人学习笔记,仅供自己参考 Note:关于 CUDA 加速双线程插值的内容博主…...

实时计算平台设计方案:913-基于100G光口的DSP+FPGA实时计算平台
基于100G光口的DSPFPGA实时计算平台 一、产品概述 基于以太网接口的实时数据智能计算一直应用于互联网、网络安全、大数据交换的场景。以DSPFPGA的方案,体现了基于硬件计算的独特性能,区别于X86GPU的计算方案,保留了高带宽特性&…...

Glide系列-自定义ModuleLoader
在当今快速发展的移动应用领域,图片的高效加载和显示对于提供流畅用户体验至关重要。Glide作为一款强大的图片加载库,已经成为Android开发者的首选工具之一。但是,你有没有遇到过Glide默认不支持的模型类型,或者需要对图片加载过程…...

设计模式——责任链模式13
责任链模式 每个流程或事物处理 像一个链表结构处理。场景由 多层部门审批,问题分级处理等。下面体现的是 不同难度的问题由不同人进行解决。 设计模式,一定要敲代码理解 传递问题实体 /*** author ggbond* date 2024年04月10日 07:48*/ public class…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
