【算法】图的存储和遍历

作者：指针不指南吗
专栏：算法篇

🐾或许会很慢，但是不可以停下🐾

1. 图的存储

• 引入

一般来说，树和图有两种存储方式，树是无环连通图，树是特殊的图，这里只讲图。

图分成两种有向图和无向图

无向图：有向图建两条边，a->b , b->a

所以说，无向图是一种特殊的有向图 , 我们只讲 有向图的存储

1.1 邻接矩阵

二维数组， g[a][b] ,a 到 b 的边

比较浪费空间，适合存储 稠密图，用的比较少

1.2 邻接表

图和部分注释转自 acwing

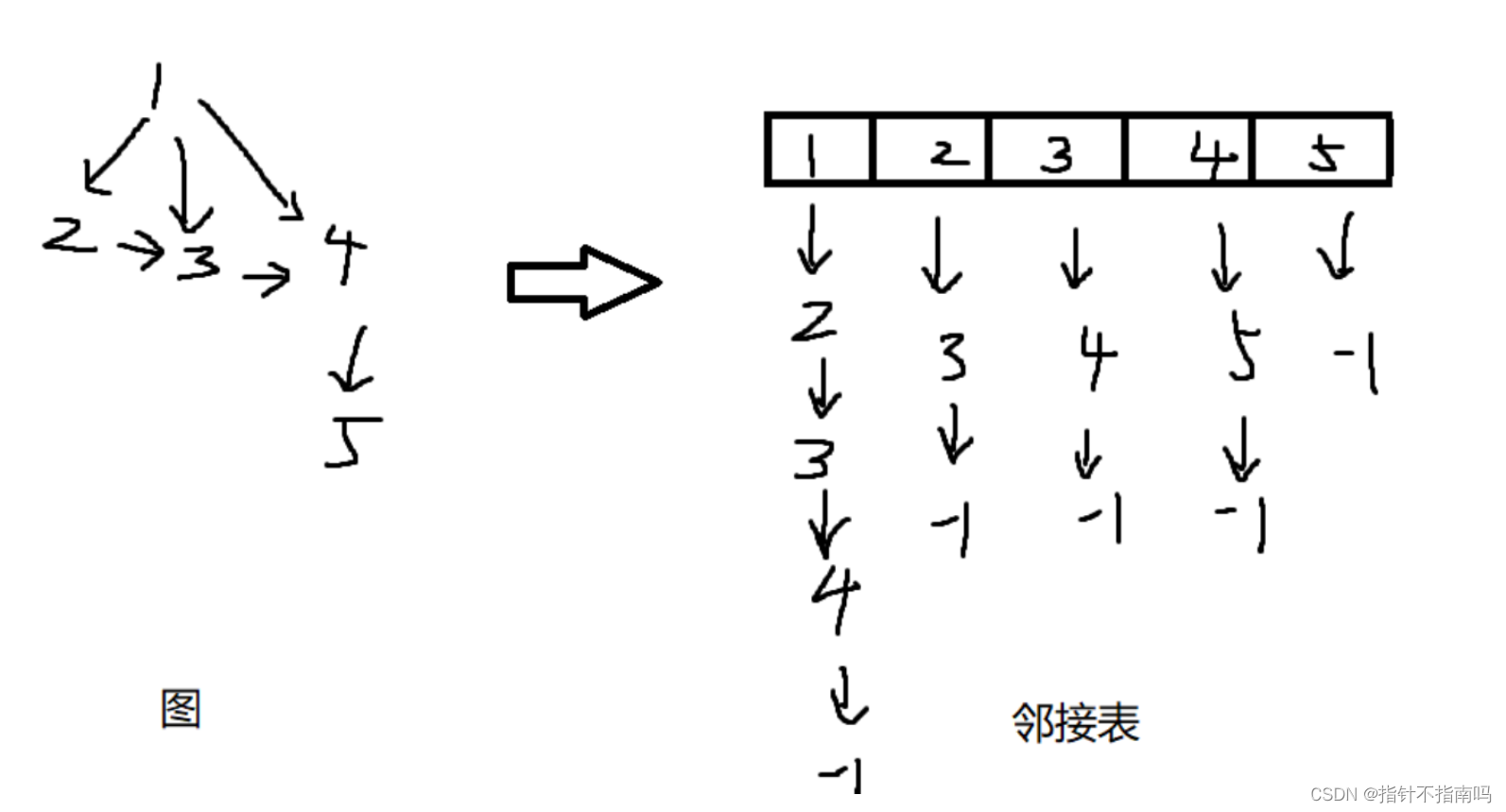
• 代码实现

#include<bits/stdc++.h>
using namespace std;//N ： 节点数量
//M：边的数量
//i : 节点的下标索引
//idx ： 边的下标索引const int N=100010,M=2*N;//h[N] : 表示 第 i 个节点的 第一条边的 idx
//ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
//e[M] : 表示 第idx 条边的 终点 表示值int h[N],e[M],ne[M],idx;void add(int a, int b)  //插入一个 a->b 的边
{e[idx]=b;  // 记录 加入的边 的终点节点, 记录值h[idx]=h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标，ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面，其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面；目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边，完成把最新的一条边插入到 链表头的操作；h[a]=idx++;   a节点开头的第一条边置为当前边，idx移动到下一条边
}int main()
{int n;cin>>n;memset(h,-1,sizeof h); //把每个头节点 初始化为 -1return 0;
}

2. 图的遍历

一般我们每个元素就遍历一次

两种搜索方式，每个点只遍历一次：深搜一边路走到黑 ；宽搜 一层一层的搜

边的权重 都相等,则使用 bfs 找最短路

2.1 dfs 遍历

• 代码模板

#include<bits/stdc++.h>
using namespace std;const int N=100010,M=N*2;  //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边int n;
int h[N],e[M],ne[M],idx;
bool st[N];void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}// 树 dfs 遍历 框架
void dfs(int u)  //遍历以 u 为根节点的子树
{if(u==n) return ;  //边界条件就是左右的点 都遍历过了for(int i=h[u];i!=-1;i=ne[i])  {int j=e[i]; // 去出当前节点编号if(!st[j]) //没有使用过，继续{st[j]=true;  //改变状态dfs(j);  //dfs 下一个节点，就是搜索以 j 为根节点的子树}}
}int main()
{cin>>n;memset(h,-1,sizeof h);  //给头节点 初始化return 0;
}

• 例题

  链接：[acwing 846.树的重心]( 846. 树的重心 - AcWing题库 )

  给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。

  请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

  重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

  输入格式

  第一行包含整数 n，表示树的结点数。

  接下来 n−1 行，每行包含两个整数 a 和 b，表示点 a 和点 b 之间存在一条边。

  输出格式

  输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

  数据范围

  1≤n≤$10^5$

  输入样例：

  9
  1 2
  1 7
  1 4
  2 8
  2 5
  4 3
  3 9
  4 6
  

  输出样例：

  4
  

• 思路

  1. 把树存在邻接表里面

  2. 开始找去除重心之后，使剩余几部分连通图中，每一部分节点最大数量 最小

     • 我们可以通过 dfs ，找到每个子树中节点数量
     • 算出一个子树的每一部分 ABC , 取他们的 最 max ，计算每一个节点的这几个部分

  

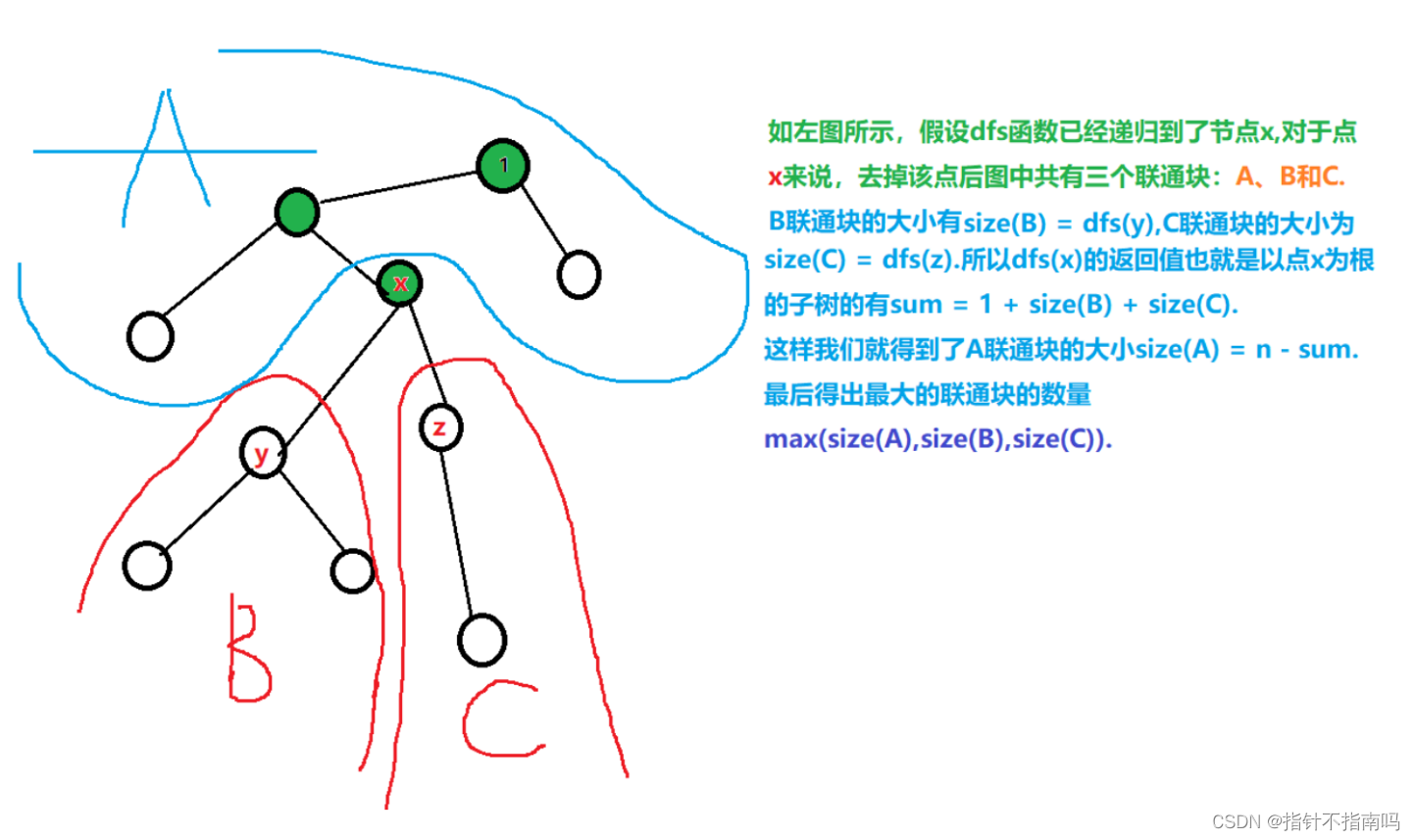
• 代码实现

  #include<bits/stdc++.h>
  using namespace std;const int N=1e5+10,M=2*N;  int n;
  int h[N],e[M],ne[M],idx;
  int ans=N;  //最小值，初始化为 一个最大数
  bool st[N];void add(int a,int b)
  {e[idx]=b,ne[idx]=h[a],h[a]=idx++;
  }int dfs(int u) //返回的是，去除 u 节点之后最大连通图的数量
  {st[u]=true;  //改变状态//size 表示子树连通块中点的数量（图中 B或者C）//sum 表示以 u 为根节点所有的子树点的数量（图中 x点+B+C）int size=0,sum=1; for(int i=h[u];i!=-1;i=ne[i])  //遍历以 u 为根节点的子树{int j=e[i];  //j 表示现在正在遍历的节点编号if (st[j]) continue;  //遍历过了，跳过进行下一个st[j]=true;  //改变状态int s=dfs(j);  //存的是，以 j 为根节点的所有子树的中点的数量size=max(size,s);  //取所有 子树中点数量最大的值 相当于比较图中的B,Csum+=s;  //sum+ 扩展的子树中点的数量}size=max(size,n-sum);  //相当于比较途中 各个部分 ABC 的最大值ans=min(size,ans);  //取最大值的最小值return sum;  //返回 以 u 为根节点的所有子树地最大值
  }int main()
  {cin>>n;memset(h,-1,sizeof h);for(int i=0;i<n;i++){int a,b;cin>>a>>b;add(a,b),add(b,a);  //注意这里是 无向图，有两条边}dfs(1);  //开始遍历树cout<<ans;  //输出结果return 0;
  }
  

2.2 bfs 遍历

• 代码模板

//宽搜框架
queue<int > q;
q.push(1);  //把编号 1 节点放进去
while(!q.empty())
{int t=q.front();q.pop();//拓展所有t可以到的节点，邻点if(/*邻点x没有被遍历过*/){q.push(x);st[x]=1;d[x]=d[t]+1;}
}

• 例题

  链接: 847. 图中点的层次 - AcWing题库

  给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环。

  所有边的长度都是 1，点的编号为 1∼n。

  请你求出 1 号点到 n 号点的最短距离，如果从 1号点无法走到 n 号点，输出 −1。

  输入格式

  第一行包含两个整数 n 和 m。

  接下来 m 行，每行包含两个整数 a 和 b，表示存在一条从 a 走到 b 的长度为 1 的边。

  输出格式

  输出一个整数，表示 1 号点到 n 号点的最短距离。

  数据范围

  1≤n,m≤$10^5$

  输入样例：

  4 5
  1 2
  2 3
  3 4
  1 3
  1 4
  

  输出样例：

  1
  

• 思路

  我们第一发现这个点,就是源点到这个点的最短路径

  首先判断出来 这道题是使用 bfs

  然后 , 图的存储, 图的遍历 模板题

• 代码实现

  #include<bits/stdc++.h>
  using namespace std;const int N=1e5+10,M=N*2;int n,m;  //n表示点，m表示边
  int h[N],e[M],ne[M],idx;
  bool st[N];
  int q[N],d[N];  //q表示队列，d表示距离void add(int a,int b)
  {e[idx]=b,ne[idx]=h[a],h[a]=idx++;
  }int bfs()
  {int hh,tt;  //hh表示队头，tt表示队尾q[0]=1;  //存储层次遍历序列 0号节点是编号为1的节点memset(d,-1,sizeof d);  //d[]==-1,表示没有被遍历过d[1]=0;  //储存每个节点到 起点 编号1 的距离while(hh<=tt){//取出 队头int t=q[hh++];//遍历t节点的每一个邻边for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];  if(d[j]==-1)  //j 没有没被扩展过{d[j]=d[t]+1;  //该点的距离+1，并且表示已经被扩展过了q[++tt]=j;  //把扩展的点放到队列里面去，压入队列}  }}return d[n]; //返回编号为 n 的节点到 起点的距离
  }int main()
  {cin>>n>>m;memset(h,-1,sizeof h);for(int i=0;i<m;i++)  //读入边{int a,b;cin>>a>>b;add(a,b);}cout<<bfs();return 0;
  }
  

  STL 队列实现 bfs

  int bfs()
  {queue<int> q;q.push(1);//  q[0]=1;  //存储层次遍历序列 0号节点是编号为1的节点memset(d,-1,sizeof d);  //d[]==-1,表示没有被遍历过d[1]=0;  //储存每个节点到 起点 编号1 的距离while(!q.empty()){int t=q.front();q.pop();for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]==-1){d[j]=d[t]+1;q.push(j);}}}
  }