运筹系列68:TSP问题Held-Karp下界的julia实现
1. 介绍
Held-Karp下界基于1tree下界,但是增加了点权重,如下图
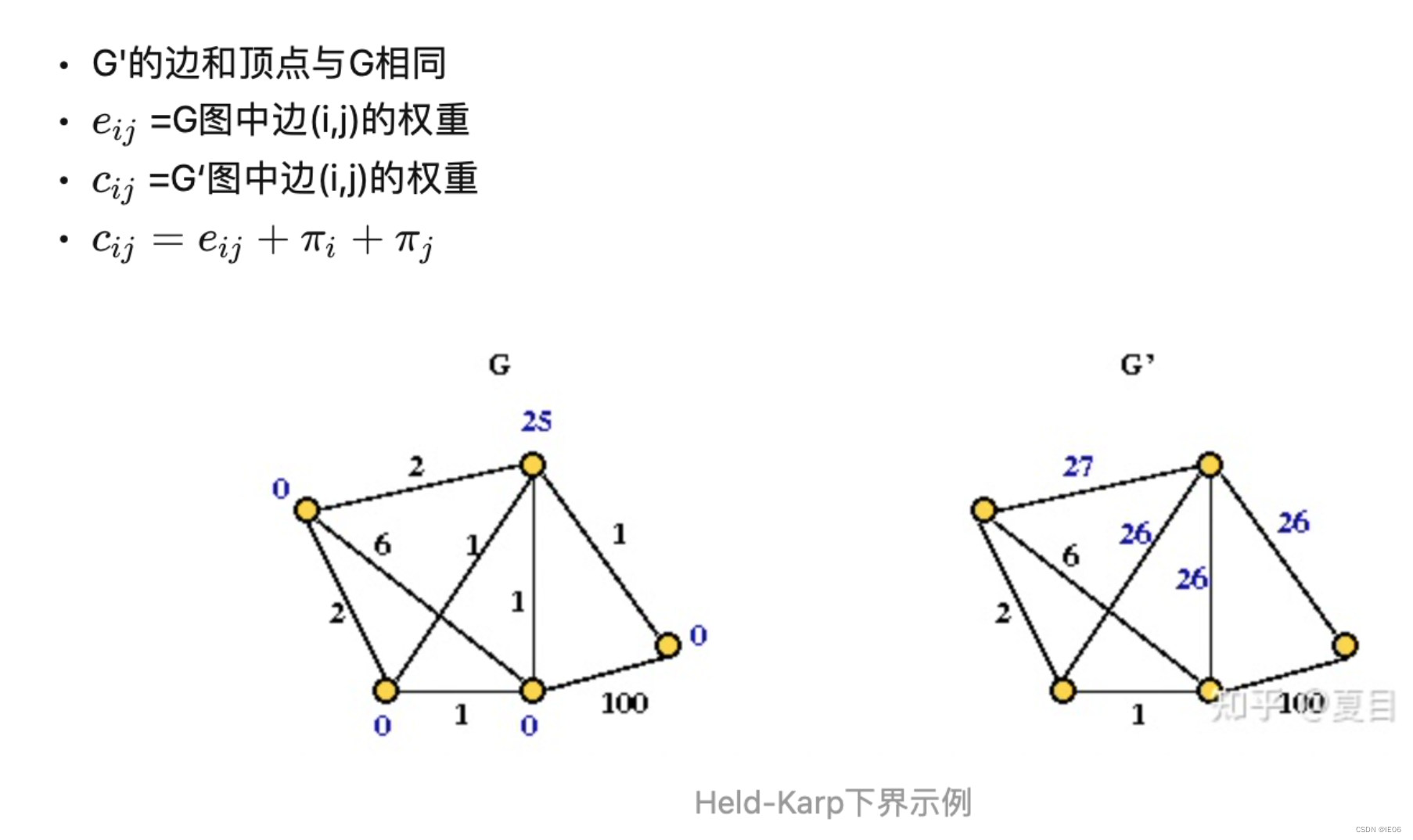
通过梯度下降的方法找到最优的π\piπ。
这里用到的1tree有下面几种:
- 全部点用来生成最小生成树,再加上所有叶子结点第二短的边中数值最大的那个
- 任意选一个点,选取它最短的两边边;然后剩下的点生成最小生成树
- 和2类似,但是枚举所有的点。
2. 代码分析
首先是根据距离列表arr,获得当前节点root最近的两条边
function minimum_two(arr,root)n = length(arr)m1=arr[1]m2=arr[1]m1_ind=1m2_ind=1for i in [1:root-1;root+1:n]if arr[i]<m1m2=m1m1=arr[i]m2_ind=m1_indm1_ind=ielseif arr[i]<m2m2=arr[i]m2_ind=iendendreturn m1_ind,m2_ind,m1,m2
end
2.1 第一种1tree
function minimum1tree(distmat,pi)distmat = distmat.+pi.+pi'mst, c = TravelingSalesmanHeuristics.minspantree(distmat)x = counter(cat([m[1] for m in mst],[m[2] for m in mst],dims=1))n = size(distmat)[1]leaves = []for i in 1:nif x[i]==1append!(leaves,i)endendmax_w = 0max_m1 = 1max_m2 = 1for leaf_ind in 1:length(leaves)leaf = leaves[leaf_ind]_,m2_ind,_,m2 = minimum_two(distmat[leaf,:],leaf)w = c+m2if w > max_wmax_w = wmax_m1 = leafmax_m2 = m2_indendendmax_v = [x[i] for i in 1:size(distmat)[1]].-2max_v[max_m1]+=1max_v[max_m2]+=1return max_w-2*sum(pi),max_v,max_m1,max_m2
end
2.2 第二种1tree
function minimum1tree(distmat,pi,first_node)distmat = distmat.+pi.+pi'm1_ind,m2_ind,m1,m2 = minimum_two(distmat[first_node,:],first_node)n = size(distmat)[1]left_nodes = [1:first_node-1;first_node+1:n]mst, c = TravelingSalesmanHeuristics.minspantree(distmat[left_nodes,left_nodes])x = counter(cat([left_nodes[m[1]] for m in mst],[left_nodes[m[2]] for m in mst],dims=1))x[first_node]=2x[m1_ind]+=1x[m2_ind]+=1w = c+m1+m2-2*sum(pi)v = [x[i] for i in 1:n].-2distmat = distmat.-pi'.-pireturn w,v
end2.3 梯度下降代码
这里使用的是第一种minimum1tree,第二种类似。
function ascent(c)n = size(c)[1]pi = zeros(n) # 初始化优化参数pibest_pi = pit = 1 # 优化步长best_w,v,m1,m2 = minimum1tree(c, pi) # 初始化w和vbest_deg = sum(v.*v) # 初始化目标函数last_v = v period = max(floor(Int,n/2), 100)initial_period = periodinitialPhase = truewhile t > 0.01p = 1while p<=periodfor i in 1:n;if v[i] == 0;last_v[i] = 0; end;endpi = pi+t*(0.7*v+0.3*last_v)last_v = vw, v, m1, m2 = minimum1tree(c, pi) deg = sum(v.*v)if deg == 0@info("* T = $t, Period = $period, BestW = $w, Norm = $deg, m1 = $m1, m2 = $m2")return w, pielseif (w > best_w && deg <= best_deg)@info("** T = $t, Period = $period, BestW = $w, Norm = $deg, m1 = $m1, m2 = $m2")best_w = wbest_pi = pibest_deg = degif initialPhase;t *= 2;end # 增加步长if p == period;period*=2;end # 增加迭代次数elseif initialPhase && p > initial_period /2@info("* T = $t, Period = $period, BestW = $w, Norm = $deg")initialPhase = falsep = 1t = t*3/4 # 第一阶段过后,开始逐步收缩步长endp+=1endt = t/2 # 每个阶段迭代完成后,都收缩步长和迭代次数进行下轮迭代period = floor(Int,period/2)endreturn best_w, best_pi
end
3. 实测结果
我们使用TSPLIB的att48进行观测,最优解为33522.0。梯度下降打印信息如下:
[ Info: ** T = 1, Period = 100, BestW = 29266.0, Norm = 34, m1 = 2, m2 = 42
[ Info: ** T = 2, Period = 100, BestW = 29333.000000000004, Norm = 34, m1 = 2, m2 = 42
[ Info: ** T = 4, Period = 100, BestW = 29463.4, Norm = 32, m1 = 2, m2 = 42
[ Info: ** T = 8, Period = 100, BestW = 29954.6, Norm = 32, m1 = 2, m2 = 42
[ Info: ** T = 16, Period = 100, BestW = 30398.2, Norm = 26, m1 = 2, m2 = 42
[ Info: ** T = 32, Period = 100, BestW = 31464.399999999998, Norm = 18, m1 = 2, m2 = 42
[ Info: ** T = 64, Period = 100, BestW = 31744.999999999993, Norm = 18, m1 = 2, m2 = 42
[ Info: ** T = 128, Period = 100, BestW = 32487.200000000004, Norm = 18, m1 = 29, m2 = 5
[ Info: * T = 256, Period = 100, BestW = 28475.4, Norm = 62
[ Info: ** T = 96.0, Period = 50, BestW = 32514.400000000012, Norm = 18, m1 = 5, m2 = 29
[ Info: ** T = 96.0, Period = 50, BestW = 32873.40000000001, Norm = 10, m1 = 5, m2 = 29
[ Info: ** T = 96.0, Period = 50, BestW = 33086.20000000001, Norm = 10, m1 = 5, m2 = 29
[ Info: ** T = 96.0, Period = 50, BestW = 33115.8, Norm = 8, m1 = 29, m2 = 5
[ Info: ** T = 48.0, Period = 25, BestW = 33168.00000000001, Norm = 8, m1 = 29, m2 = 34
[ Info: ** T = 48.0, Period = 25, BestW = 33292.399999999994, Norm = 6, m1 = 29, m2 = 34
[ Info: ** T = 24.0, Period = 12, BestW = 33391.399999999994, Norm = 6, m1 = 29, m2 = 34
[ Info: ** T = 24.0, Period = 12, BestW = 33410.6, Norm = 6, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 6, BestW = 33411.200000000004, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 12, BestW = 33417.19999999999, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 12, BestW = 33421.200000000004, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 24, BestW = 33423.6, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 24, BestW = 33424.799999999996, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 24, BestW = 33424.80000000001, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 12.0, Period = 24, BestW = 33435.200000000004, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 6.0, Period = 12, BestW = 33441.00000000001, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 3.0, Period = 6, BestW = 33442.399999999994, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 3.0, Period = 6, BestW = 33443.4, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 3.0, Period = 12, BestW = 33444.299999999996, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 1.5, Period = 12, BestW = 33444.9, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 1.5, Period = 12, BestW = 33445.350000000006, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 1.5, Period = 12, BestW = 33446.59999999999, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 0.375, Period = 3, BestW = 33447.31249999999, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 0.1875, Period = 3, BestW = 33447.55625, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 0.1875, Period = 6, BestW = 33447.706249999996, Norm = 2, m1 = 29, m2 = 34
[ Info: ** T = 0.09375, Period = 3, BestW = 33447.825, Norm = 2, m1 = 29, m2 = 34
此时结果如下:
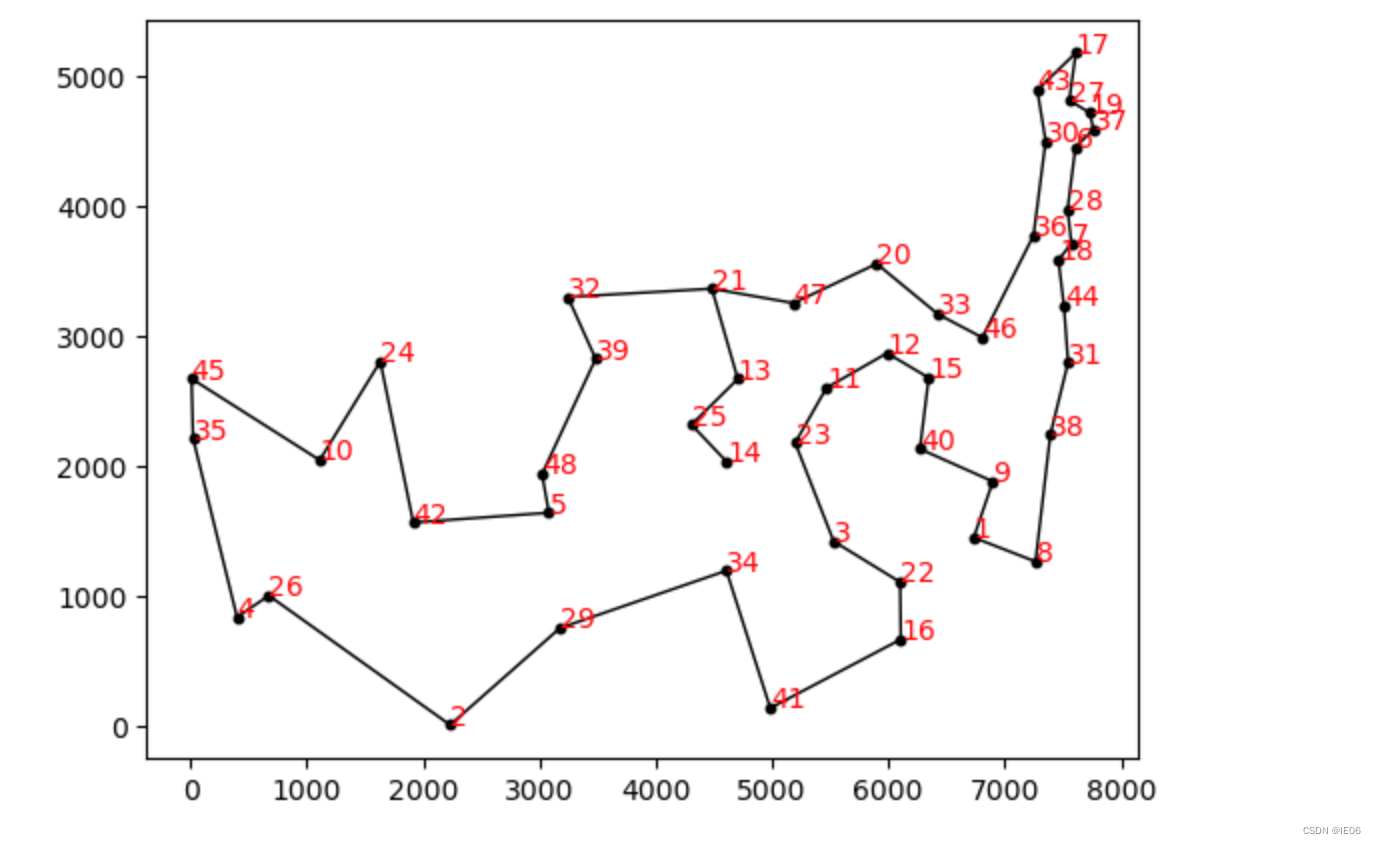
最优结果如下,已非常接近。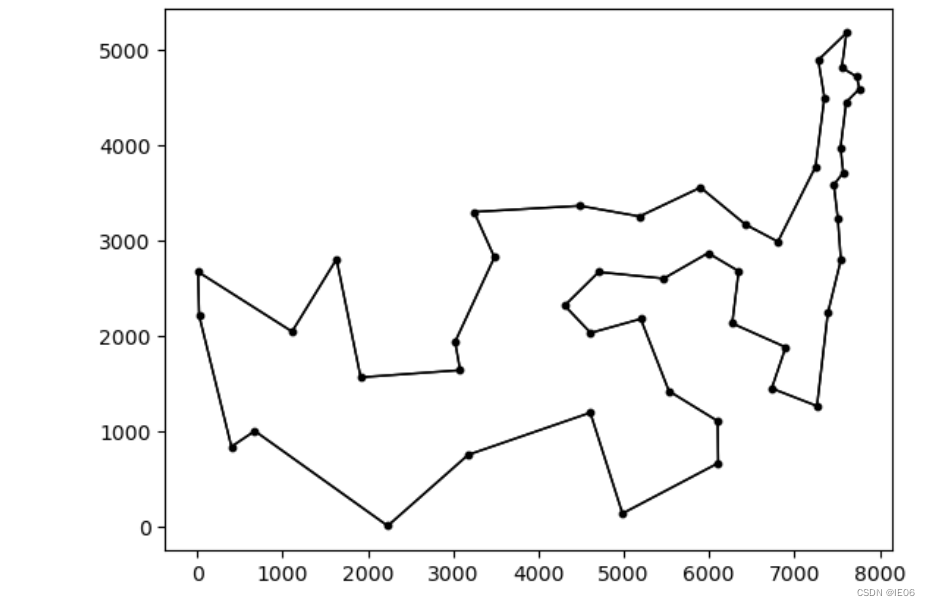
相关文章:

运筹系列68:TSP问题Held-Karp下界的julia实现
1. 介绍 Held-Karp下界基于1tree下界,但是增加了点权重,如下图 通过梯度下降的方法找到最优的π\piπ。 这里用到的1tree有下面几种: 全部点用来生成最小生成树,再加上所有叶子结点第二短的边中数值最大的那个任意选一个点&…...
)
神经影像信号处理总成(EEG、SEEG、MRI、CT)
目录一. EEG(脑电图)1.1 脑波1.2 伪迹1.2.1 眼动伪迹1.2.2 肌电伪迹1.2.3 运动伪迹1.2.4 心电伪迹1.2.5 血管波伪迹1.2.6 50Hz和静电干扰1.3 伪迹去除方法1.3.1 避免伪迹产生法1.3.2 直接移除法1.3.3 伪迹消除法二. SEEG(立体脑电图)三. CT(计算机断层扫描ÿ…...

ZooKeeper 进阶:基本介绍
zppkeeper是什么 zookeeper是一个高性能、开源的分布式应用协调服务,它提供了简单原始的功能,分布式应用可以基于它实现更高级的服务,比如实现同步(分布式锁)、配置管理、集群管理。它被设计为易于编程,使用文件系统目录树作为数…...

CSS的常用元素属性,显示模式,盒模型,弹性布局
目录 1.常用元素属性 1.1字体属性 设置字体 设置大小 字体粗细 文字样式 1.2文本属性 文字颜色 文字对齐 编辑文本装饰 文本缩进 编辑行高 编辑1.3背景属性 背景颜色 背景位置 背景尺寸 1.4圆角矩形 2.元素的显示模式 2.1块级元素(display:block) 2.…...
【20230308】串口接收数据分包问题处理(Linux)
1 问题背景 一包数据可能由于某些传输原因,经常出现一包数据分成几包的情况。 2 解决方法 2.1 通过设定最小读取字符和读取超时时间 可以使用termios结构体来控制终端设备的输入输出。可以通过VTIME和VMIN的值结合起来共同控制对输入的读取。此外,两…...

数据库复试问题总结
数据库复试问题 由《数据库系统概论(第5版)》总结而来,用于本人研究生复试准备。也欢迎各位准研究生们学习使用。 文章目录数据库复试问题1、三级模式结构及二级映射有什么优点?2、关系模型中的完整性约束是哪几类?3、SQL的特点?…...

Linux操作系统安装——服务控制
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。座右铭:海不辞水,故能成其大;山不辞石,故能成其高。个人主页:小李会科技的…...
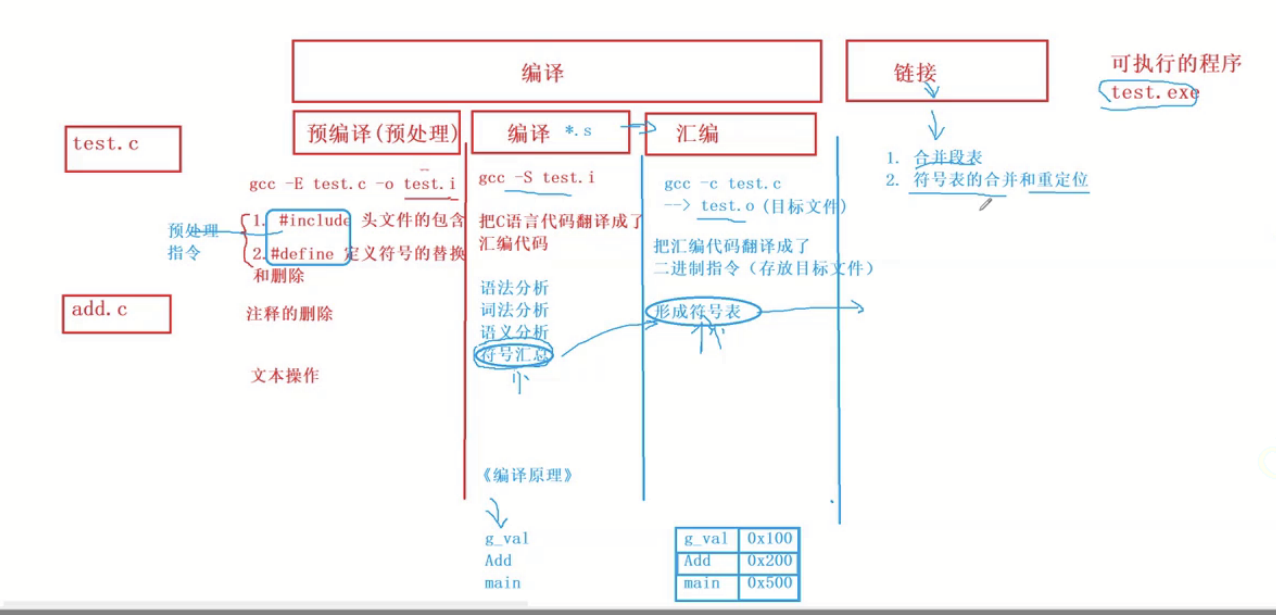
【C语言】编译+链接
一、程序的翻译环境和执行环境 在ANSI C的任何一种实现中,存在两个不同的环境。 第1种是翻译环境,在这个环境中源代码被转换为可执行的机器指令。 第2种是执行环境,它用于实际执行代码。详解编译链接翻译环境1.组成一个程序的每个源文件通过…...

为「IT女神勋章」而战
大家好,我是空空star,今天为「IT女神勋章」而战 文章目录前言一、IT女神勋章二、绘制爱心1.htmlcssjs来源:一行代码代码效果2.python来源:C知道代码效果3.go来源:复制代码片代码效果4.java来源:download代码…...

JS 动画 之 setInterval、requestAnimationFram
帧率:一秒中内页面刷新的次数,一般为60FPS,每一帧的时间是1000/6016.67ms setInterval 当我们使用setInterval做动画时,有两点会影响动画效果 由于setInterval是异步任务(宏任务),会放到异步队…...
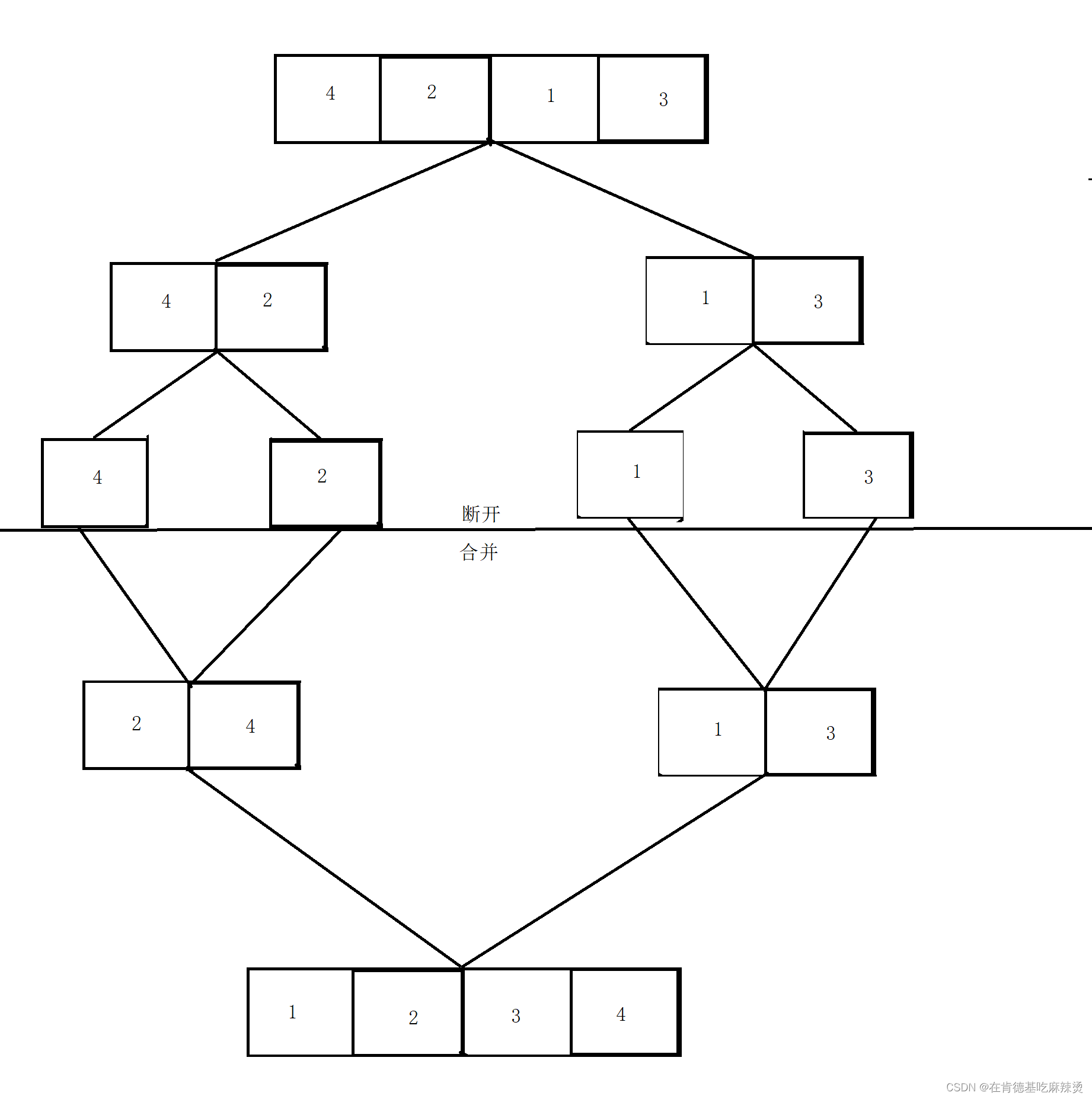
【LeetCode——排序链表】
文章目录排序链表二、解题思路:二.实现的代码总结:排序链表 一道链表排序题,链接在这里 二、解题思路: 解题思路:使用归并排序(用递归实现) 第一步:先找到链表的中间节点 第二步…...

二叉树的遍历(前序、中序、后序)| C语言
目录 0.写在前面 1.前序遍历 步骤详解 代码实现 2.中序遍历 步骤详解 代码实现 3.后序遍历 步骤详解 代码实现 0.写在前面 认识二叉树结构最简单的方式就是遍历二叉树。所谓遍历二叉树就是按照某种特定的规则,对二叉树的每一个节点进行访问,…...

【建议收藏】深入浅出Yolo目标检测算法(含Python实现源码)
深入浅出Yolo目标检测算法(含Python实现源码) 文章目录深入浅出Yolo目标检测算法(含Python实现源码)1. One-stage & Two-stage2. Yolo详解2.1 Yolo命名2.2 端到端输入输出2.3 Yolo中的标定框2.4 Yolo网络结构2.5 Yolo的算法流…...
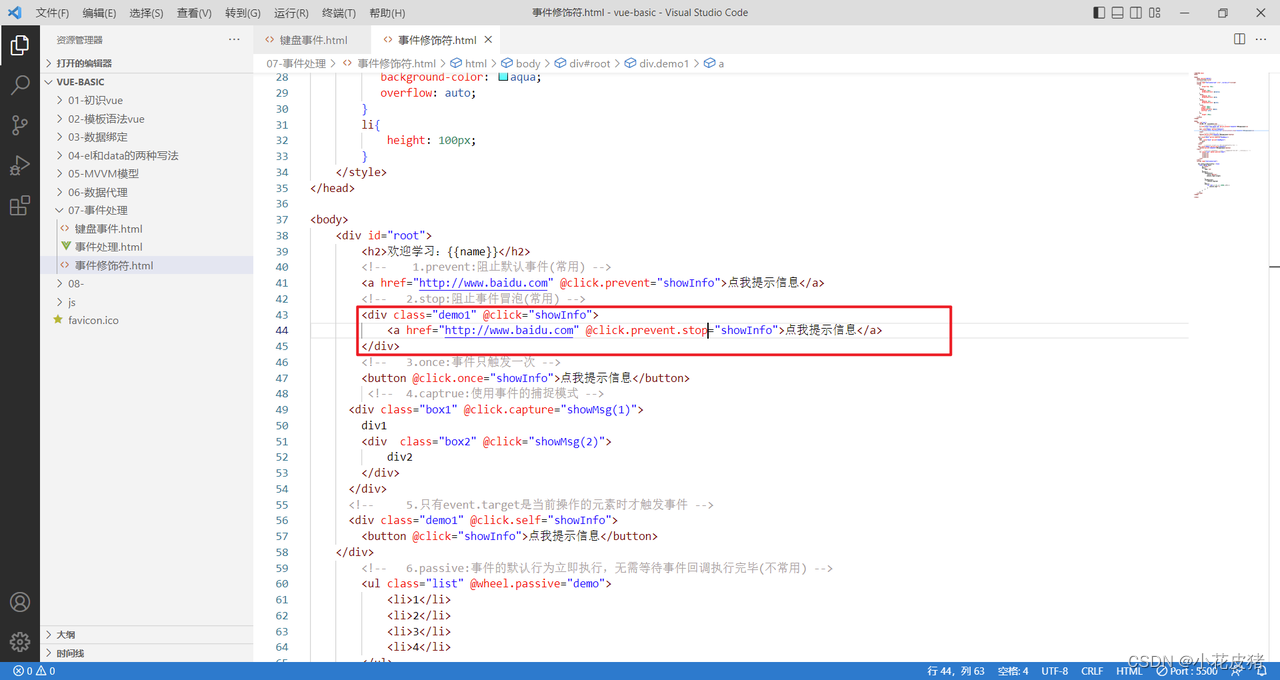
Vue常见的事件修饰符
前言 vue一共给我们准备了6个事件修饰符,前三个比较常用,后三个少见,这里着重讲下前三个 1.prevent:阻止默认事件(常用) 2. stop:阻止事件冒泡(常用) 3. once:事件只触发一次(常用) 4.captrue:使用事件的捕捉模式(不常用) 5.self:只有event…...
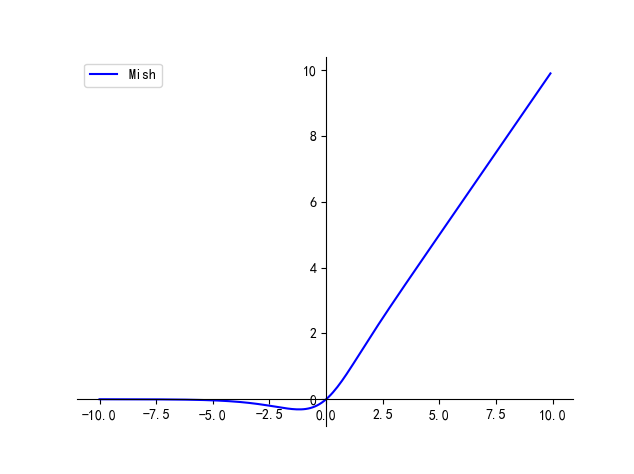
【卷积神经网络】激活函数 | Tanh / Sigmoid / ReLU / Leaky ReLU / ELU / SiLU / GeLU
文章目录一、Tanh二、Sigmoid三、ReLU四、Leaky ReLU五、ELU六、SiLU七、Mish本文主要介绍卷积神经网络中常用的激活函数及其各自的优缺点 最简单的激活函数被称为线性激活,其中没有应用任何转换。 一个仅由线性激活函数组成的网络很容易训练,但不能学习…...

刷题记录:牛客NC24048[USACO 2017 Jan P]Promotion Counting 求子树的逆序对个数
传送门:牛客 题目描述 奶牛们又一次试图创建一家创业公司,还是没有从过去的经验中吸取教训–牛是可怕的管理者! 为了方便,把奶牛从 1∼n1\sim n1∼n 编号,把公司组织成一棵树,1 号奶牛作为总裁(这棵树的根…...

MpAndroidChart3最强实践攻略
本篇主要总结下Android非常火爆的一个三方库MpAndroidChart的使用。可能在大多数情况下,我们很少会在Android端去开发图表。但如果说去做一些金融财经类、工厂类、大数据类等的app,那么绝对会用到MpAndroidChart。 一、前言 2018年,那年的我…...
:事务管理ACID)
Spring笔记(9):事务管理ACID
一、事务管理 一个数据库事务是一个被视为单一的工作单元操作序列。 事务管理有四个原则,被成为ACID: Atomicity 原子性—— 事务作为独立单元进行操作,整个序列是一体的,操作全都成功或失败。Consistency 一致性—— 引用完整…...

io流 知识点+代码实例
需求 : 如何实现读写文件内部的内容?流 : 数据以先入先出的方式进行流动相当于管道,作用用来传输数据数据源-->流-->目的地流的分类 :流向分 : 以程序为中心输入流输出流操作单元 :字节流 : 万能流字符流 : 只能操作纯文本文件功能分 :节点流 : 真实实现读写的功能流(包…...
【MySQL】P8 多表查询(2) - 连接查询 联合查询
连接查询以及联合查询多表查询概述连接查询内连接隐式内连接显式内连接外连接左外连接右外连接自连接联合查询多表查询概述 建表语句见上一篇博文:https://blog.csdn.net/weixin_43098506/article/details/129402302 e.g.e.g.e.g. select * from emp, dept where e…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
