5月7日监控二叉树+斐波那契数
968.监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
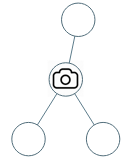
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
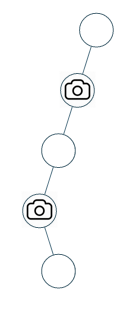
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路
想半天想不出来然后去看了各路大神的题解,对比之下发现官方题解的说法完全是在冒充人类。
首先我们先要确定从二叉树的下面往上看,为什么不自顶向下呢?因为头节点放不放摄像头也就省下一个摄像头,但是叶子节点放不放摄像头省下的是指数级的摄像头。
那么从下往上看我们首先想到的是二叉树的后序遍历法(左-右-中),所以本题我们使用递归法来解。
并且,如果要达成局部最优的话,我们一定是在叶子节点的父节点安装摄像头,让所用摄像头最少,达成全局最优。
所以,大体思路就是从低向上遍历二叉树,先给叶子节点父节点放摄像头,然后隔两个节点放一个摄像头,直到到根节点。
但是怎样隔两个节点放一个摄像头呢?此时我们就需要状态转移的公式来记录每个节点的状态。每个节点可能有三种状态:
0:该节点无覆盖
1:该节点有摄像头
2:该节点有覆盖
空节点一律视为有覆盖的情况,因为若把空节点视为无覆盖,那么空节点的父节点——叶子节点就必须放置一个摄像头,这与本意冲突;若把空节点视为有摄像头,那么叶子节点就为有覆盖,那么隔两个节点才会放一个摄像头,实际上没有监控到叶子节点,所以空节点只能视为有覆盖。
那么,对于每个节点的处理逻辑我们可以分为四类情况:
1、左右节点都有覆盖:该节点一定无覆盖
2、左右节点至少有一个无覆盖:该节点一定放摄像头
3、左右节点至少有一个摄像头:该节点一定有覆盖
4、头节点无覆盖:头节点再加一个摄像头。
代码
class Solution {int res=0;public int minCameraCover(TreeNode root) {return dfs(root)==0?res+1:res;}private int dfs(TreeNode node){if(node==null){return 2;}int left=dfs(node.left);int right=dfs(node.right);if(left==0||right==0){res++;return 1;}if(left==1||right==1){return 2;}return 0;}}灵茶山艾府的思路我没理解,二刷的时候再研究。
509.斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路
经典递归解法:
class Solution {public int fib(int n) {if(n==1){return 1;}else if(n==0){return 0;}else {return fib(n-1)+fib(n-2);}}}dp解法:
确定dp数组含义
dp[i]的定义为:第i个数的斐波那契数值为dp[i]
递推公式:dp[i] = dp[i - 1] + dp[i - 2];
初始化:dp[0]=0,dp[1]=1
代码
class Solution {public int fib(int n) {if (n <= 1) return n; int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int index = 2; index <= n; index++){dp[index] = dp[index - 1] + dp[index - 2];}return dp[n];}
}空间复杂度可以进一步优化,因为不用维护整个dp数组:
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}相关文章:

5月7日监控二叉树+斐波那契数
968.监控二叉树 给定一个二叉树,我们在树的节点上安装摄像头。 节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。 计算监控树的所有节点所需的最小摄像头数量。 示例 1: 输入:[0,0,null,0,0] 输出:1 解释ÿ…...

C++类的设计编程示例
一、银行账户类 【问题描述】 定义银行账户BankAccount类。 私有数据成员:余额balance(整型)。 公有成员方法: 无参构造方法BankAccount():将账户余额初始化为0; 带参构造方法BankAccount(int m)࿱…...
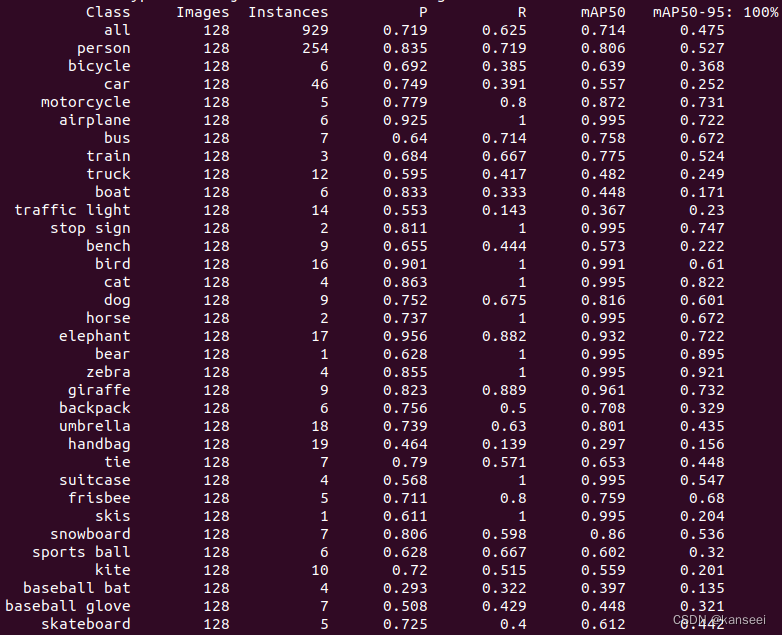
YOLOv5 V7.0 - rknn模型的验证 输出精度(P)、召回率(R)、mAP50、mAP50-95
1.简介 RKNN官方没有提供YOLOv5模型的验证工具,而YOLOv5自带的验证工具只能验证pytorch、ONNX等常见格式的模型性能,无法运行rknn格式。考虑到YOLOv5模型转换为rknn会有一定的精度损失,但是需要具体数值才能进行评估,所以需要一个…...
CUDA、CUDNN、Pytorch三者之间的关系
这个东西嘛,我一开始真的是一头雾水,安装起来真是麻烦死了。但是随着要复现的项目越来越多,我也不得不去学会他们是什么,以及他们之间的关系。 首先,一台电脑里面允许有多种版本的cuda存在,然后cuda分为run…...

vue-cli2,vue-cli3,vite 生产环境去掉console.log
console.log一般都是在开发环境下使用的,在生产环境下需要去除 ,如果手动删除未免也太累了,我们可以用插件对于具体环境全局处理。 vue-cli2 项目build 下面webpack.prod.config.js 文件中: plugins: [new webpack.DefinePlugin({process.en…...
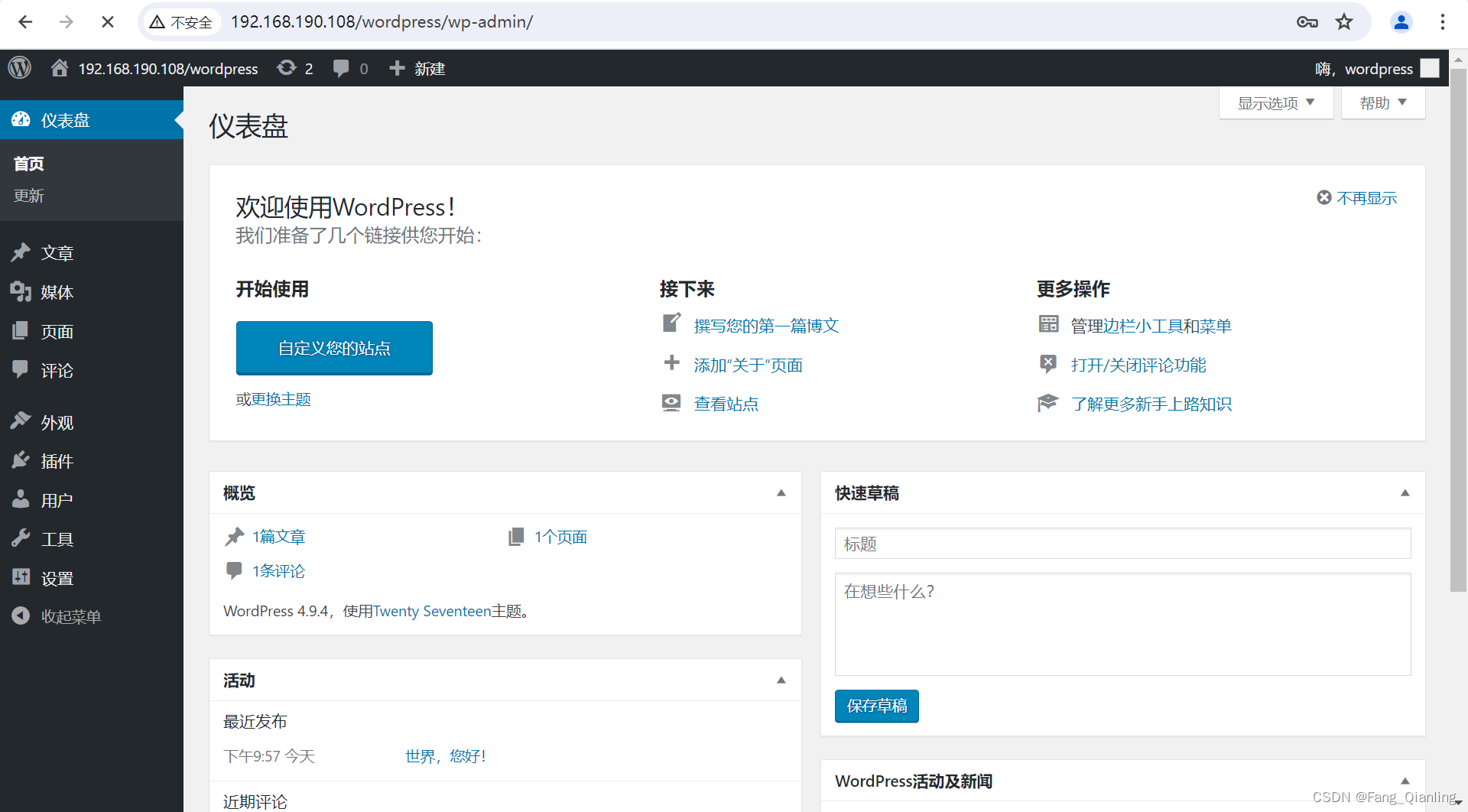
Docker-Compose编排LNMP并部署WordPress
前言 随着云计算和容器化技术的快速发展,使用 Docker Compose 编排 LNMP 环境已经成为快速部署 Web 应用程序的一种流行方式。LNMP 环境由 Linux、Nginx、MySQL 和 PHP 组成,为运行 Web 应用提供了稳定的基础。本文将介绍如何通过 Docker Compose 编排 …...

附录C:招聘流程
< 回到目录 附录C:招聘流程 _xxx_公司的招聘 使命 只雇佣顶级人才。 他们是能够胜任工作,并与 _(你的公司名称)_ 的企业文化相匹配的超级明星。 方法 记分卡。招聘经理创建一份文件,详细描述此职位的工作内容…...
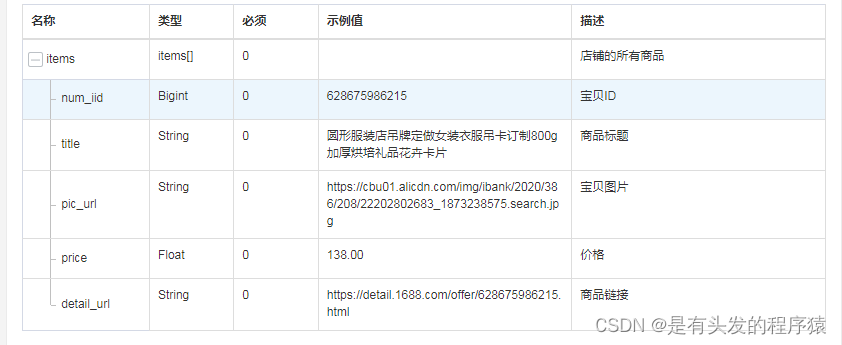
1688快速获取整店铺列表 采集接口php Python
在电子商务的浪潮中,1688平台作为中国领先的批发交易平台,为广大商家提供了一个展示和销售商品的广阔舞台;然而,要在众多店铺中脱颖而出,快速获取商品列表并进行有效营销是关键。 竞争对手分析 价格比较:…...

CTF-WEB(MISC)
安全攻防知识——CTF之MISC - 知乎 CTF之MISC杂项从入门到放弃_ctf杂项 你的名字-CSDN博客 CTF MICS笔记总结_archpr 掩码攻击-CSDN博客 一、图片隐写 CTF杂项---文件类型识别、分离、合并、隐写_ctf图片分离-CSDN博客 EXIF(Exchangeable Image File)是…...

Ubuntu如何更换 PyTorch 版本
环境: Ubuntu22.04 WLS2 问题描述: Ubuntu如何更换 PyTorch 版本考虑安装一个为 CUDA 11.5 编译的 PyTorch 版本。如何安装旧版本 解决方案: 决定不升级CUDA版本,而是使用一个与CUDA 11.5兼容的PyTorch版本,您可…...

python flask css样式无效
解释: Flask是一个Python的轻量级Web框架,它没有为CSS提供任何内置的支持。如果你在Flask项目中引入了CSS文件,但是这个CSS没有生效,可能的原因有: 路径不正确:你的CSS文件没有放在正确的目录下࿰…...
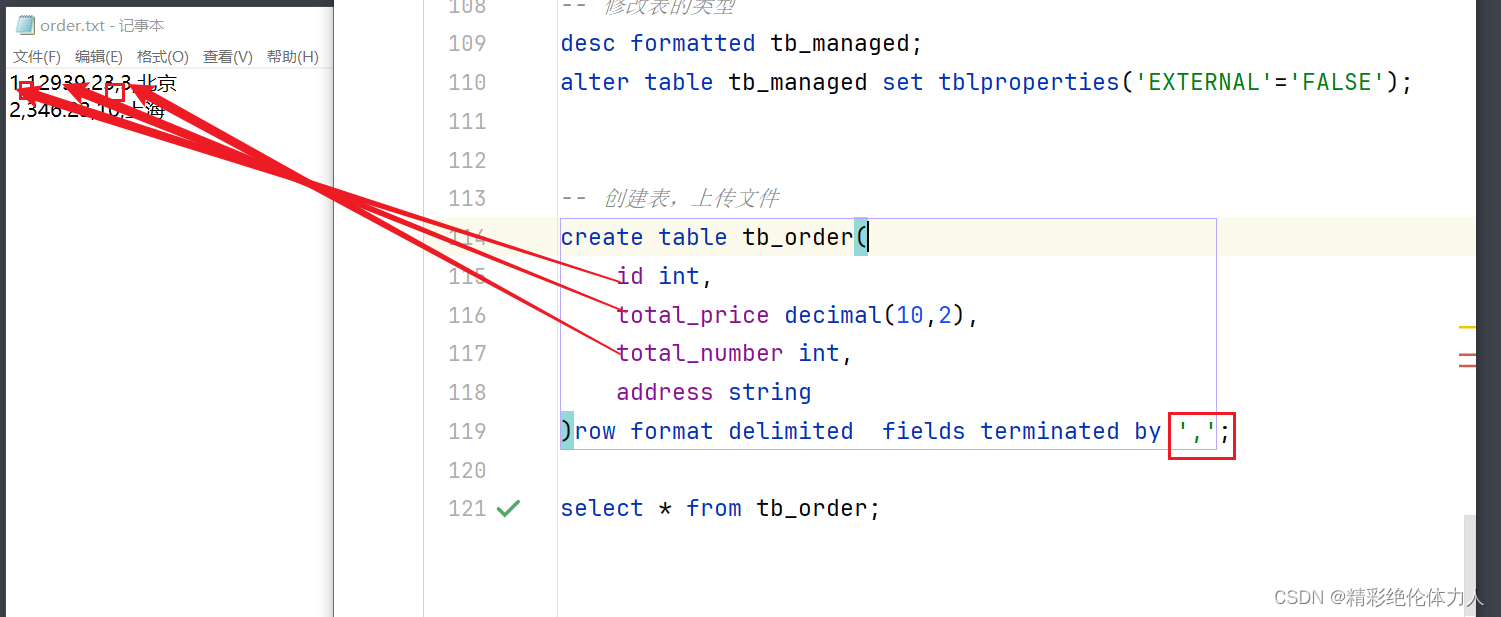
大数据学习笔记14-Hive基础2
一、数据字段类型 数据类型 :LanguageManual Types - Apache Hive - Apache Software Foundation 基本数据类型 数值相关类型 整数 tinyint smallint int bigint 小数 float double decimal 精度最高 日期类型 date 日期 timestamps 日期时间 字符串类型 s…...
)
vue3 下载图片(包括多图片下载)
单图片下载 //使用 download(https://img1.baidu.com/it/u1493209339,2544178769&fm253&app138&sizew931&n0&fJPEG&fmtauto?sec1715101200&t854f3434686cfd2cba9d6a528597d15c)//下载逻辑 const download async (modelUrl) > {const respons…...

LabVIEW如何通过子VI更改主VI控件属性?
在LabVIEW中,可以通过使用Local Variable或Property Node来实现主VI控件属性的更改。这些方法可以在主VI和子VI之间传递数据和控件属性。 Local Variable: 使用Local Variable可以在子VI中直接访问并修改主VI中的控件属性。在子VI中创建Local Variable,并…...

关于MS-DOS时代的回忆
目录 一、MS-DOS是什么? 二、MS-DOS的主要功能有哪些? 三、MS-DOS的怎么运行的? 四、微软开源MS-DOS源代码 五、高手与漂亮女同学 一、MS-DOS是什么? MS-DOS(Microsoft Disk Operating System)是微软公…...
)
数据库索引(Mysql)
简述:数据库索引是加速数据检索,提高查询效率的一种数据结构 语法规则 创建索引 --通用语法规则 --[内容] 可选参数 --UNIQUE: 可选关键字,用于创建唯一索引,确保索引列的值是唯一的 CREATE [UNIQUE] INDEX 索引名 ON 表名(字段名,...) [ASC | DESC];…...

异常-Exception
异常介绍 基本概念 Java语言中,将程序执行中发生的不正常情况称为“异常”。(开发过程中的语法错误和逻辑错误不是异常)执行过程中所发生的异常事件可分为两大类 1,Error(错误):Java虚拟机无法…...
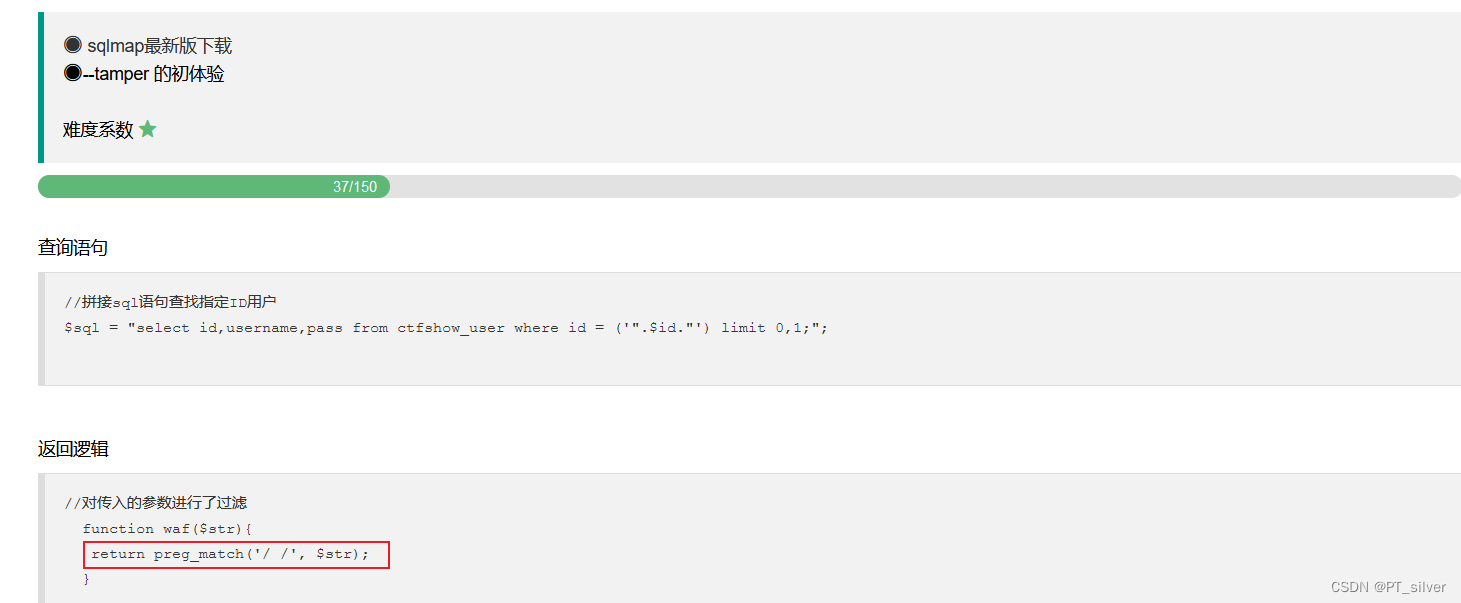
ctfshow——SQL注入
文章目录 SQL注入基本流程普通SQL注入布尔盲注时间盲注报错注入——extractvalue()报错注入——updataxml()Sqlmap的用法 web 171——正常联合查询web 172——查看源代码、联合查询web 173——查看源代码、联合查询web 174——布尔盲注web 176web 177——过滤空格web 178——过…...
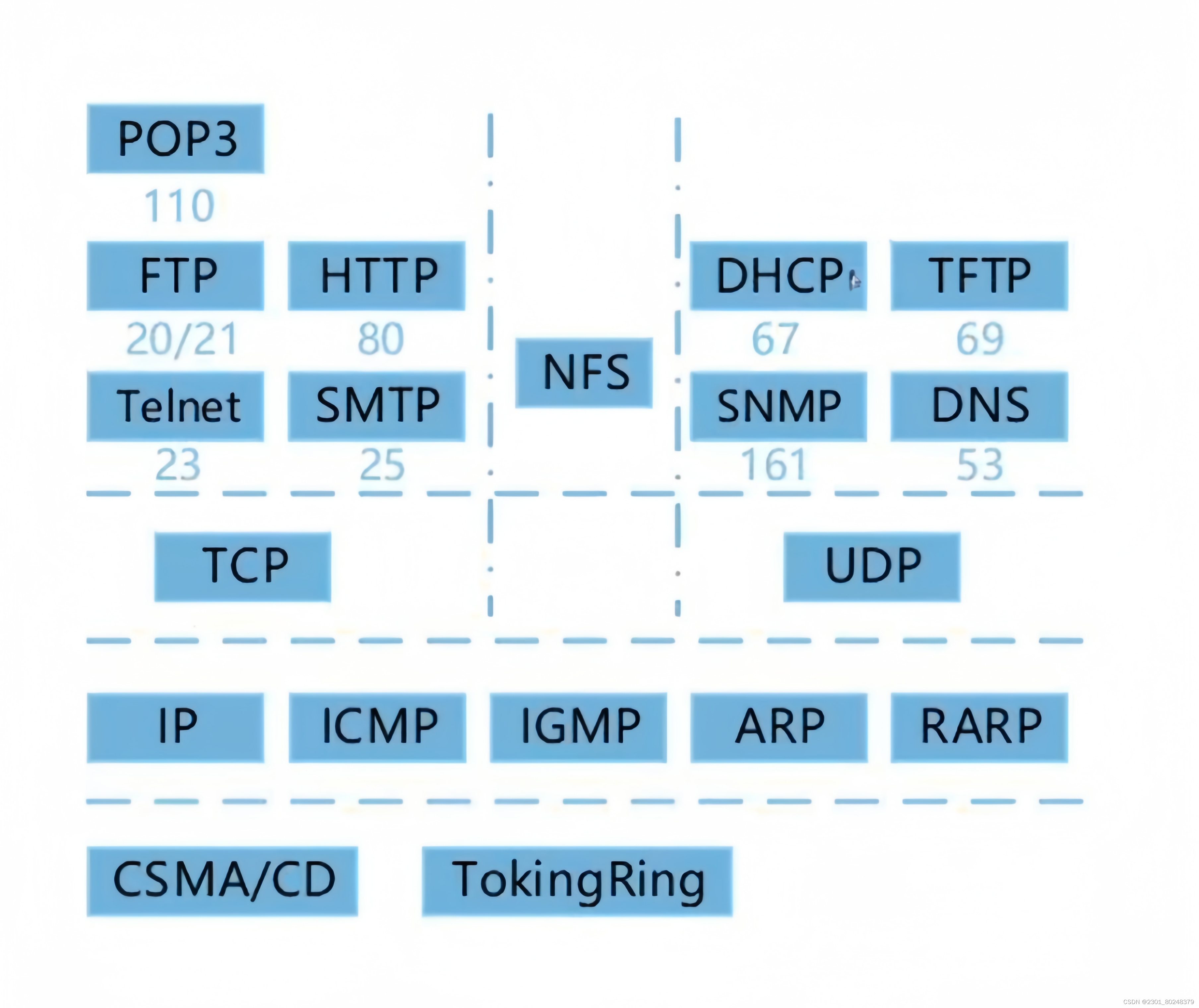
第十三章 计算机网络
这里写目录标题 1.网络设备2.协议簇2.1电子邮件(传输层)2.2地址解析(网际层)2.3DHCP(动态主动配置协议)2.4URL(统一资源定位器)2.5IP地址和子网掩码 1.网络设备 物理层:中继器,集线器(多路中继器) 数据链路层:网桥,交换机(多端口…...

商品详情 API 返回值说明
商品详情API接口在多个领域和场景中都有广泛的应用,以下是一些常见的应用场景: 竞品分析:企业可以利用商品详情API接口获取竞品的所有详细信息,如价格、发货地、上架时间、销售量等。通过分析这些竞品信息,企业可以更…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
