【Java 刷题记录】前缀和
前缀和
25. 一维前缀和
示例1:
输入:
3 2 1 2 4 1 2 2 3输出:
3 6
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint n = in.nextInt();int q = in.nextInt();long[] dp = new long[n + 1];for(int i = 1; i < n + 1; i++) {int number = in.nextInt();dp[i] = dp[i - 1] + number;}for(int i = 0; i < q; i++) {int start = in.nextInt();int end = in.nextInt();System.out.println(dp[end] - dp[start - 1]);} }}
}
26. 二维前缀和
示例1:
输入:
3 4 3 1 2 3 4 3 2 1 0 1 5 7 8 1 1 2 2 1 1 3 3 1 2 3 4输出:
8 25 32备注:
读入数据可能很大,请注意读写时间。
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint n = in.nextInt();int m = in.nextInt();int q = in.nextInt();long[][] dp = new long[n + 1][m + 1];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {int num = in.nextInt();dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + num;}}for(int i = 1; i <= q; i++) {int a = in.nextInt();int b = in.nextInt();int c = in.nextInt();int d = in.nextInt();long num = dp[a - 1][d] + dp[c][b - 1] - dp[a - 1][b - 1];System.out.println(dp[c][d] - num);}}}
}
27. 寻找数组的中心下标
给你一个整数数组
nums,请计算数组的 中心下标 。数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为
0,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回
-1。示例 1:
输入:nums = [1, 7, 3, 6, 5, 6] 输出:3 解释: 中心下标是 3 。 左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 , 右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。示例 2:
输入:nums = [1, 2, 3] 输出:-1 解释: 数组中不存在满足此条件的中心下标。示例 3:
输入:nums = [2, 1, -1] 输出:0 解释: 中心下标是 0 。 左侧数之和 sum = 0 ,(下标 0 左侧不存在元素), 右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。提示:
- 1 <= nums.length <= 104
-1000 <= nums[i] <= 1000
class Solution {public int pivotIndex(int[] nums) {int n = nums.length;long[] dp = new long[n + 1];for(int i = 1; i <= n; i++) {dp[i] = dp[i - 1] + nums[i - 1];}long sum = dp[n];for(int i = 1; i <= n; i++) {if(sum - dp[i] == dp[i - 1]) return i - 1;}return -1;}
}
28. 除自身以外数组的乘积
给你一个整数数组
nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 **不要使用除法,**且在
O(*n*)时间复杂度内完成此题。示例 1:
输入: nums = [1,2,3,4] 输出: [24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]提示:
- 2 <= nums.length <= 105
-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内**进阶:**你可以在
O(1)的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;// 1. 初始化前缀🐔、后缀🐔数组int[] f = new int[n + 1];f[0] = 1;int[] g = new int[n + 1];g[n] = 1;for(int left = 1, right = n - 1; left <= n && right >= 0; left++, right--) {f[left] = nums[left - 1] * f[left - 1];g[right] = nums[right] * g[right + 1];}// 2. 使用数组封装结果集int[] ret = new int[n];for(int i = 0; i < n; i++) {ret[i] = f[i] * g[i + 1];}return ret;}
}
29. 和为 K 的子数组
给你一个整数数组
nums和一个整数k,请你统计并返回 该数组中和为k的子数组的个数 。子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2 输出:2示例 2:
输入:nums = [1,2,3], k = 3 输出:2提示:
- 1 <= nums.length <= 2 * 104
-1000 <= nums[i] <= 1000- -107 <= k <= 107
class Solution {public int subarraySum(int[] nums, int k) {// 1. 初始化哈希表Map<Integer, Integer> hash = new HashMap<>();hash.put(0, 1);// 2. 遍历数组进行统计int sum = 0;int ret = 0;for(int num : nums) {// 当前前缀和sum += num;// 统计ret += hash.getOrDefault(sum - k, 0);// sum 加入哈希表hash.put(sum, hash.getOrDefault(sum, 0) + 1);}return ret;}
}
30. 和可被 K 整除的子数组
给定一个整数数组
nums和一个整数k,返回其中元素之和可被k整除的(连续、非空) 子数组 的数目。子数组 是数组的 连续 部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5 输出:7 解释: 有 7 个子数组满足其元素之和可被 k = 5 整除: [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]示例 2:
输入: nums = [5], k = 9 输出: 0提示:
- 1 <= nums.length <= 3 * 104
- -104 <= nums[i] <= 104
- 2 <= k <= 104

class Solution {public int subarraysDivByK(int[] nums, int k) {// 1. 初始化哈希表int[] hash = new int[k];hash[0] = 1;// 2. 统计int sum = 0;int ret = 0;for(int num : nums) {sum += num;int m = (sum % k + k) % k;ret += hash[m];hash[m]++;}return ret;}
}
31. 连续数组
给定一个二进制数组
nums, 找到含有相同数量的0和1的最长连续子数组,并返回该子数组的长度。示例 1:
输入: nums = [0,1] 输出: 2 说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。示例 2:
输入: nums = [0,1,0] 输出: 2 说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。提示:
- 1 <= nums.length <= 105
nums[i]不是0就是1
class Solution {public int findMaxLength(int[] nums) {int n = nums.length;// 1. 转化for(int i = 0; i < n; i++) {nums[i] = nums[i] == 0 ? -1 : 1;}// 2. 初始化哈希表Map<Integer, Integer> hash = new HashMap<>();hash.put(0, -1);// 3. 遍历数组进行统计int sum = 0;int ret = 0;for(int i = 0; i < n; i++) {sum += nums[i];// 前面有没有前缀和为 sum 的if(hash.containsKey(sum)) {// 更新 retret = Math.max(i - hash.get(sum), ret);} else {// 进入哈希表hash.put(sum, i);}}return ret;}
}
32. 矩阵区域和
给你一个
m x n的矩阵mat和一个整数k,请你返回一个矩阵answer,其中每个answer[i][j]是所有满足下述条件的元素mat[r][c]的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1 输出:[[12,21,16],[27,45,33],[24,39,28]]示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2 输出:[[45,45,45],[45,45,45],[45,45,45]]提示:
m == mat.lengthn == mat[i].length1 <= m, n, k <= 1001 <= mat[i][j] <= 100
class Solution {public int sum(int[][] dp, int i, int j, int k, int m, int n) {int x1 = i - k + 1;int y1 = j - k + 1;int x2 = i + k + 1;int y2 = j + k + 1;x1 = x1 >= 1 ? x1 : 1;y1 = y1 >= 1 ? y1 : 1;x2 = x2 <= m ? x2 : m;y2 = y2 <= n ? y2 : n;return sum(dp, x1, y1, x2, y2);}public int sum(int[][] dp, int x1, int y1, int x2, int y2) {return dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];}public int[][] matrixBlockSum(int[][] mat, int k) {// 1. 搞一个前缀和矩阵int m = mat.length;int n = mat[0].length;int[][] dp = new int[m + 1][n + 1];for(int i = 1; i <= m; i++) {for(int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];}}// 2. 构造结果集int[][] ret = new int[m][n];for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {ret[i][j] = sum(dp, i, j, k, m, n);}}return ret;}
}
相关文章:

【Java 刷题记录】前缀和
前缀和 25. 一维前缀和 示例1: 输入: 3 2 1 2 4 1 2 2 3输出: 3 6import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) {Scanner in new Scanner(S…...

NVIDIA: RULER新测量方法让大模型现形
1 引言 最近在人工智能系统工程和语言模型设计方面的进展已经实现了语言模型上下文长度的高效扩展。以前的工作通常采用合成任务,如密钥检索和大海捞针来评估长上下文语言模型(LMs)。然而,这些评估在不同工作中使用不一致,仅揭示了检索能力,无法衡量其他形式的长上下文理解。 …...

2024数学-微积分和线性代数/本科研究生专业考试/考研/论文/重点公式考点汇总/最难公式投票
## 整体公式汇总列表 http://www.deepnlp.org/equation/category/math #### 微积分 ## 几何级数http://www.deepnlp.org/equation/arithmetic-and-geometric-progressions ## 级数收敛http://www.deepnlp.org/equation/convergence-of-series ## 二项式展开 http://www.dee…...
:Leetcode1005、134、135(难得有一天能完全独立做出题目))
代码随想录训练营Day33(贪心算法):Leetcode1005、134、135(难得有一天能完全独立做出题目)
Leetcode1005: 题目描述: 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数…...
Flutter笔记:Widgets Easier组件库(12)使用消息吐丝(Notify Toasts)
Flutter笔记 Widgets Easier组件库(12)使用消息吐丝(Notify Toasts) - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 29114848416…...

从《春色寄情人》学习如何面对死亡
经典台词,很震撼又很实用,记录一下。 ❤️01 有的时候好人不长命百岁,是因为老天爷觉得他们太累,让他们提前休息了! ❤️02 跟我们亲近的人离世,有可能是老天给我们发的信号,提醒我们ÿ…...

使用moveit控制机械臂
在这篇博客中,我们将详细探讨如何利用Python和Robot Operating System(ROS)配合MoveIt! 控制机械臂执行精确的抓取任务。机械臂技术在工业自动化、医疗服务以及研究领域扮演着越来越关键的角色。本文将通过介绍安装必要的软件、编写控制脚本以…...
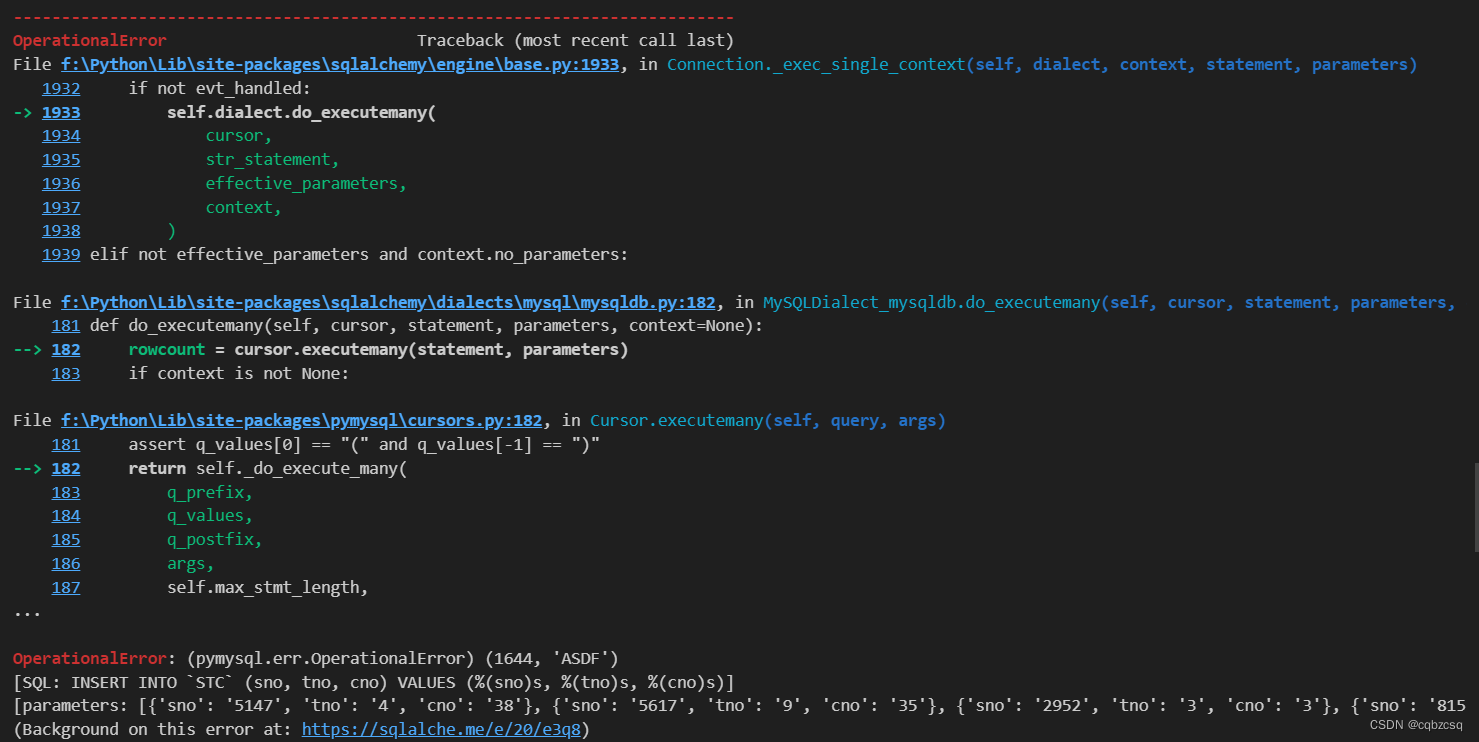
Mysql报错红温集锦(一)(ipynb配置、pymysql登录、密码带@、to_sql如何加速、触发器SIGNAL阻止插入数据)
一、jupyter notebook无法使用%sql来添加sql代码 可能原因: 1、没装jupyter和notebook库、没装ipython-sql库 pip install jupyter notebook ipython-sql 另外如果是vscode的话还需要安装一些相关的插件 2、没load_ext %load_ext sql 3、没正确的登录到mysql…...

ASP.NET Core SignalR 配置与集成测试究极指南
这篇文章也可以在我的博客中查看 前言 哥们最近都在埋头苦干,沉默是金,有一段时间没更新博客了。然而今儿SignalR集成测试实属是给我整破防了。虽说SignalR是.NET官方维护的实时通信库,已经开发了有十几年,甚至已经编入至了core…...
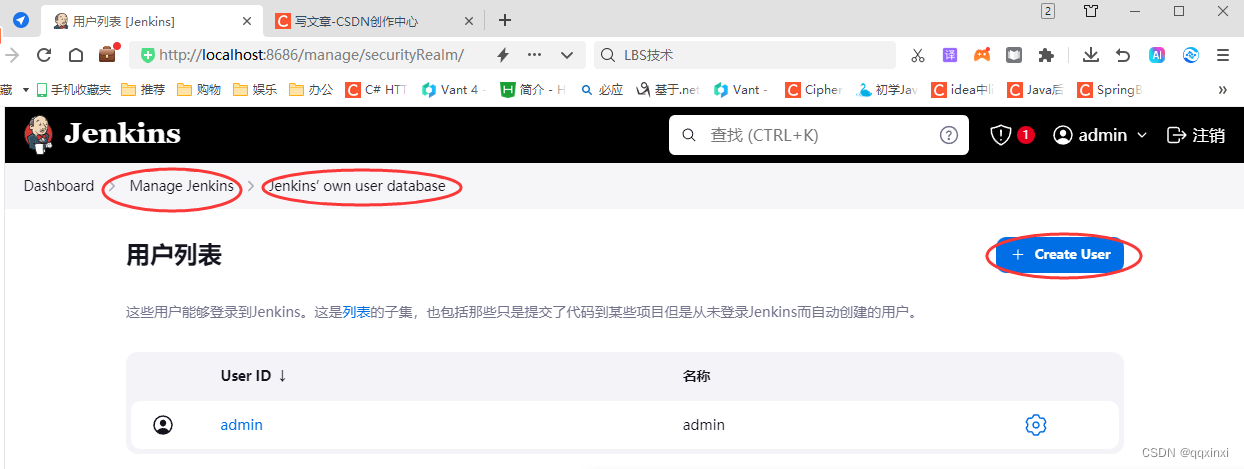
JENKINS 安装,学习运维从这里开始
Download and deployJenkins – an open source automation server which enables developers around the world to reliably build, test, and deploy their softwarehttps://www.jenkins.io/download/首先点击上面。下载Jenkins 为了学习,从windows开始&#x…...

大语言模型从Scaling Laws到MoE
1、摩尔定律和伸缩法则 摩尔定律(Moores law)是由英特尔(Intel)创始人之一戈登摩尔提出的。其内容为:集成电路上可容纳的晶体管数目,约每隔两年便会增加一倍;而经常被引用的“18个月”…...

四级英语翻译随堂笔记
降维表达:中译英,英译英 没有强调主语,没有说明主语:用被动 但如果实在不行,再增添主语 不会就不翻译,不要乱翻译 以xxx为背景:against the backdrop of the xxx eg:against the backdrop of…...

Nacos支持的配置格式及其在微服务架构中的应用
今天,我想和大家探讨一下Nacos这一重要的微服务组件,特别是它所支持的配置格式以及这些格式在微服务架构中的应用。 一、Nacos简介 Nacos是阿里巴巴开源的一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。它提供了服务发现、配置管理…...
-OD统一考试(C卷D卷))
2024年华为OD机试真题-小明找位置-(C++)-OD统一考试(C卷D卷)
题目描述: 小朋友出操,按学号从小到大排成一列;小明来迟了,请你给小明出个主意,让他尽快找到他应该排的位置。 算法复杂度要求不高于nLog(n);学号为整数类型,队列规模<=10000; 输入描述: 1、第一行:输入已排成队列的小朋友的学号(正整数),以”,”隔开; …...
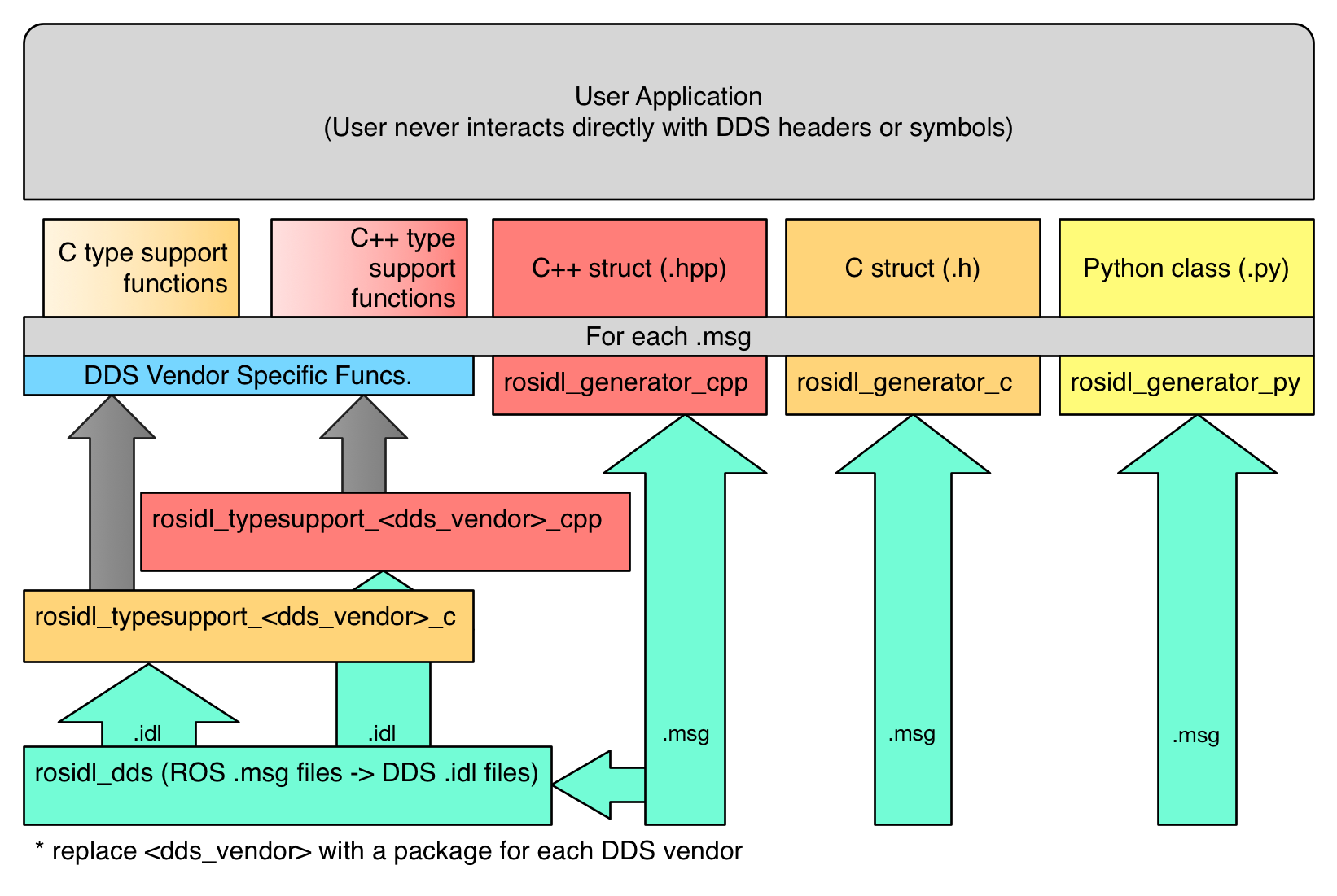
机器人系统ros2内部接口介绍
内部 ROS 接口是公共 C API ,供创建客户端库或添加新的底层中间件的开发人员使用,但不适合典型 ROS 用户使用。 ROS客户端库提供大多数 ROS 用户熟悉的面向用户的API,并且可能采用多种编程语言。 内部API架构概述 内部接口主要有两个&#x…...

跟随Facebook的足迹:社交媒体背后的探索之旅
在当今数字化时代,社交媒体已经成为了人们日常生活中不可或缺的一部分。而在这庞大的社交媒体网络中,Facebook作为其中的巨头,一直在引领着潮流。从创立之初的一个大学社交网络到如今的全球性平台,Facebook的发展历程承载了无数故…...

面试题分享之Java并发篇
注意:文章若有错误的地方,欢迎评论区里面指正 🍭 系列文章目录 面试题分享之Java集合篇(三) 面试题分享之Java集合篇(二) 面试题分享之Java基础篇(三) 前言 今天给小…...

bpmn-js 多实例配置MultiInstanceLoopCharacteristics实现或签会签
使用bpmn-js流程图开发过程中会遇到会签和或签的问题,这个时候我们就需要使用多实例配置来实现BPMN 2.0的配置实现了,多实例任务,是从流程编辑概念之初也就是Activiti时期就存在的一个方式。所谓的多实例任务也就是字面意思,一个任务由多个人完成,常见于我们的审批流程的或…...
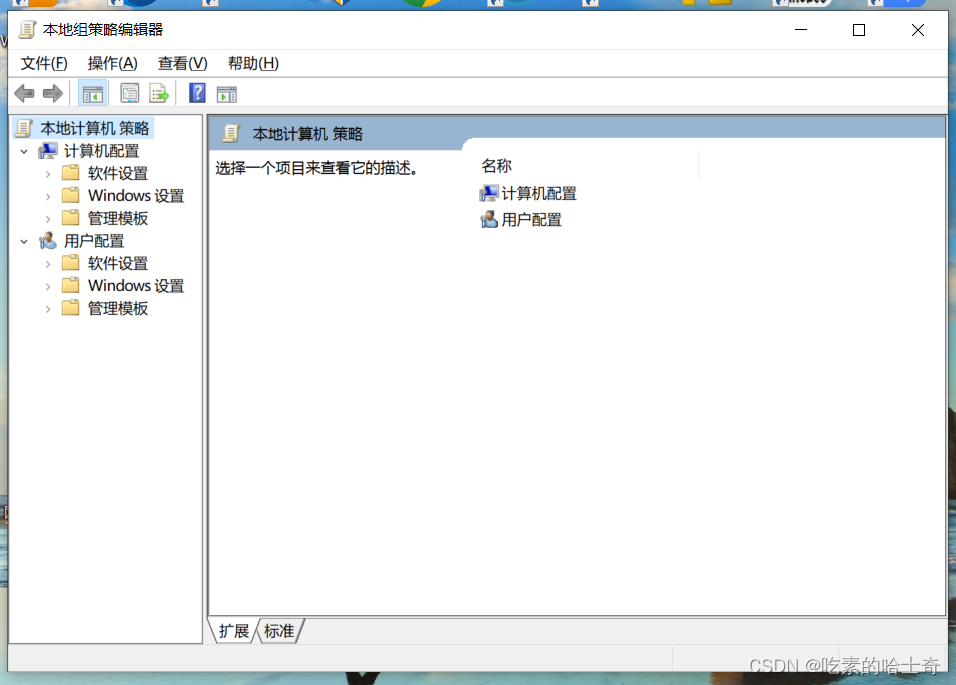
【gpedit.msc】组策略编辑器的安装,针对windows家庭版,没有此功能
创建一个记事本文件然后放入以下内容 echo offpushd "%~dp0"dir /b %systemroot%\Windows\servicing\Packages\Microsoft-Windows-GroupPolicy-ClientExtensions-Package~3*.mum >gp.txtdir /b %systemroot%\servicing\Packages\Microsoft-Windows-GroupPolicy-…...
带EXCEL附件邮件发送相关代码
1.查看生成的邮件 2.1 非面向对象的方式(demo直接copy即可) REPORT Z12. DATA: IT_DOCUMENT_DATA TYPE SODOCCHGI1,IT_CONTENT_TEXT TYPE STANDARD TABLE OF SOLISTI1 WITH HEADER LINE,IT_PACKING_LIST TYPE TABLE OF SOPCKLSTI1 WITH HEADER LIN…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...


