(第15天)【leetcode题解】459、重复的子字符串
目录
- 459、重复的子字符串
- 题目描述
- 暴力匹配
- 思路
- 代码
- 字符串匹配
- 思路
- 代码
- 与暴力匹配的不同
- KMP解法
- 思路
- 代码
- KMP算法的核心和用途
459、重复的子字符串
题目描述
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
暴力匹配
思路
- 推理
- 如果存在这样的子串,那么这个子串一定是s的前缀。
- s的长度n一定是子串长度n1的整数倍
- s中的元素s[i]与往前移n1的元素s[i-n1]相同
- 方法
因此从小到大枚举出所有可能的子串长度n1,再对这个子串进行上述的判断即可。
优化:这个子串至少要在s中重复一次,所以n1的范围为[1,n/2]。
代码
class Solution {
public:bool repeatedSubstringPattern(string s) {int n = s.size();//i代表子串的长度,应从1开始for (int i = 1; i <= n / 2; i++) {//判断该子串是否为目标子串if (n % i == 0) {bool match = true;//判断之后的字符往前移子串长度i之后是否相等//从子串之后开始遍历整个字符串for (int j = i; j < n; j++) {if (s[j] != s[j - i]) {match = false;break;} }if (match) return true;}}return false;}
};
时间复杂度:O(n2);枚举子串的时间复杂度为O(n),遍历判断子串的时间复杂度为O(n)。
空间复杂度:O(1);
字符串匹配
思路
- 如果s满足题目要求,那么s具有以下性质:
- 设s的长度为n,子串长度s1为n1.
- 可以把s写成
n/n1个子串s1排列的形式 : s——>s1s1s1s1…- 那么把第一个s1移到最后面,字符串s不变
- 根据性质,可以证明:
- 因为
1 <= n1 < n,那么把两个字符串s连在一起得到S- 把连在一起后的字符串S移除前后第一个元素
- 这时,字符串s一定是拼接串S的子串
- 根据证明结果,得到方法:
- 拼接两个字符串s
- 移除第一个和最后一个字符
- 如果s是其中的子串,则满足题目要求
代码
class Solution {
public:bool repeatedSubstringPattern(string s) {return (s + s).find(s, 1) != s.size();}
};
与暴力匹配的不同
通过推理,得到一种满足要求是的情况,只要针对这个情况进行判断即可。
KMP解法
思路
- 假设推理
- 假设这个文本串由重复子串组成
- 找到这个文本串的最长公共前后缀
- 文本串切割掉最长公共前后缀,剩下的就是重复子串
- 可用的结论
- 设文本串s由
n个长度为x的子串组成,则文本串全长为nx。- 最长公共前后缀由
m个长度为x的子串组成,长度为mx。- 则重复子串长度为
(n-m)x。n-m=1- 当全长
nx对重复子串长度(n-m)x取余等于0时(即nx % (n-m)x == 0 or nx % x == 0),证明(n-m)x代表的子串为重复子字符串。
- 方法
- 求出next数组,next数组长度为len
- 使用next数组存储文本串中最长公共前后缀的长度
next[len - 1]- 如果
len % (len -next[len - 1]) == 0,则表明存在重复子字符串
代码
class Solution {
public://得出next数组void getNext(int* next, string& s) {//初始化int j = 0;//前缀末尾从0开始next[0] = j;//从长度为2的子串开始求最长公共前后缀长度for (int i = 1; i < s.size(); i++) {//前后缀末尾不匹配时while (j >0 && s[i] != s[j]) j = next[j - 1];//j回退//前后缀末尾匹配时if (s[i] == s[j]) {j++;//j(和i)往后移一位}next[i] = j;//下标j为当前子串(末尾下标为i)的最长公共前后缀长度}}bool repeatedSubstringPattern(string s) {int next[s.size()];//创建长度为字符串长度的前缀表getNext(&next[0], s);//使用最长公共前后缀长度判断是否由重复的子字符串组成int len = s.size();//next[len - 1] == 0时,证明整个字符串最长公共前后缀长度为0//根据推理得出的结论:当len % (len - next[len-1]) == 0 时证明(有重复的子字符串/最后一段字符串为重复子字符串)if (next[len - 1] != 0 && len % (len - next[len-1]) == 0) return true;return false;}
};
时间复杂度:O(n);得到前缀表时遍历字符串需要O(n),判断重复子字符串只用了固定的操作数。
空间复杂度:O(n);需要前缀表存储字符串的所有前缀子串(包括它自身)的最长公共前后缀长度。
KMP算法的核心和用途
- 核心
- 前缀表next,其中存储了字符串的最长公共前后缀长度。
- 匹配时,使用前缀表记录的最长公共前后缀长度来进行回退。
- 总结:存储字符串的最长公共前后缀长度的前缀表、回退思想。
- 用途
- 使用前缀表回退查找子字符串。
- 使用前缀表中记录的最长公共前后缀长度来进行一些数字上的判断。
相关文章:
【leetcode题解】459、重复的子字符串)
(第15天)【leetcode题解】459、重复的子字符串
目录 459、重复的子字符串题目描述暴力匹配思路代码 字符串匹配思路代码与暴力匹配的不同 KMP解法思路代码KMP算法的核心和用途 459、重复的子字符串 题目描述 给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。 暴力匹配 思路 推理 如果…...
PostgreSQL的学习心得和知识总结(一百四十二)|深入理解PostgreSQL数据库数据库之 Continuous Integration
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...

【外币兑换,简单贪心】
小明刚从美国回来,发现手上还有一些未用完的美金,于是想去银行兑换成人民币。可是听说最近人民币将会升值,并从金融机构得到了接下来十二个月可能的美元对人民币汇率,现在,小明想要在接下来一年中把美金都兑换成人民币…...
数据库入门(sql文档+命令行)
一.基础知识 1.SQL(Structured Query Language)结构化查询语言分类: DDL数据定义语言用来定义数据库对象:数据库、表、字段DML数据操作语言对数据库进行增删改查DQL数据查询语言查询数据库中表的信息DCL数据控制语言用来创建数据…...
【机器学习300问】84、AdaGrad算法是为了解决什么问题?
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题,解决这个问题的过程称为最优化。因为参数空间非常复杂,无法轻易找到最优解,而且在深度神经网络中,参数的数量非常庞大,导致最优化问…...

Java算法-力扣leetcode-14. 最长公共前缀
14. 最长公共前缀 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 ""。 示例 1: 输入: strs ["flower","flow","flight"] 输出: "fl"示…...
视频拼接融合产品的产品与架构设计(二)
视频拼接融合产品的产品与架构设计一 以上是第一期,以前思考的时候还是比较着急,现在思考的更多了,现实世界的拼接更加需要我们沉下心来做,尤其是对于更多画面,画面更加清晰怎么做 本篇章不在于其他功能,在…...

【docker 】push 镜像到私服
查看镜像 docker images把这个hello-world 推送到私服 docker push hello-world:latest 报错了。不能推送。需要标记镜像 标记Docker镜像 docker tag hello-world:latest 192.168.2.1:5000/hello-world:latest 将Docker镜像推送到私服 docker push 192.168.2.1:5000/hello…...
Java框架精品项目【用于个人学习】
源码获取:私聊回复【项目关键字】获取 更多选题参考: Java练手项目 & 个人学习等选题参考 推荐菜鸟教程Java学习、Javatpoint学习 前言 大家好,我是二哈喇子,此博文整理了各种项目需求 此文下的项目用于博主自己学习&#x…...
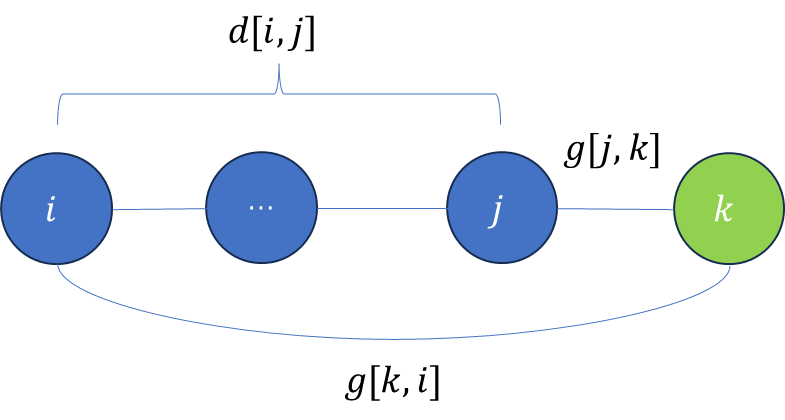
每周一算法:无向图的最小环
题目链接 观光之旅 题目描述 给定一张无向图,求图中一个至少包含 3 3 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小。 该问题称为无向图的最小环问题。 你需要输出最小环的方案,若最小环不唯一,输出…...
分布式websocket IM即时通讯聊天开源项目如何启动
前言 自己之前分享了分布式websocket的视频有同学去fork项目了,自己启动一下更方便理解项目嘛。然后把项目启动需要的东西全部梳理出来。支持群聊单聊,表情包以及发送图片。 支持消息可靠,消息防重,消息有序。同时基础架构有分布式权限&…...
环境准备写个简单例子(小白手册)-20240506)
tensorflow学习笔记(1)环境准备写个简单例子(小白手册)-20240506
一、安装python、tensorflow 1、Mac上默认python已经安装,自带pip 2、pip3 install tensorflow 如果报错,提示pip3版本较低,可以根据提示来更新pip3:/Library/Developer/CommandLineTools/usr/bin/python3 -m pip install --upgrade pip 3、然后再使用pip3来安装tensor…...
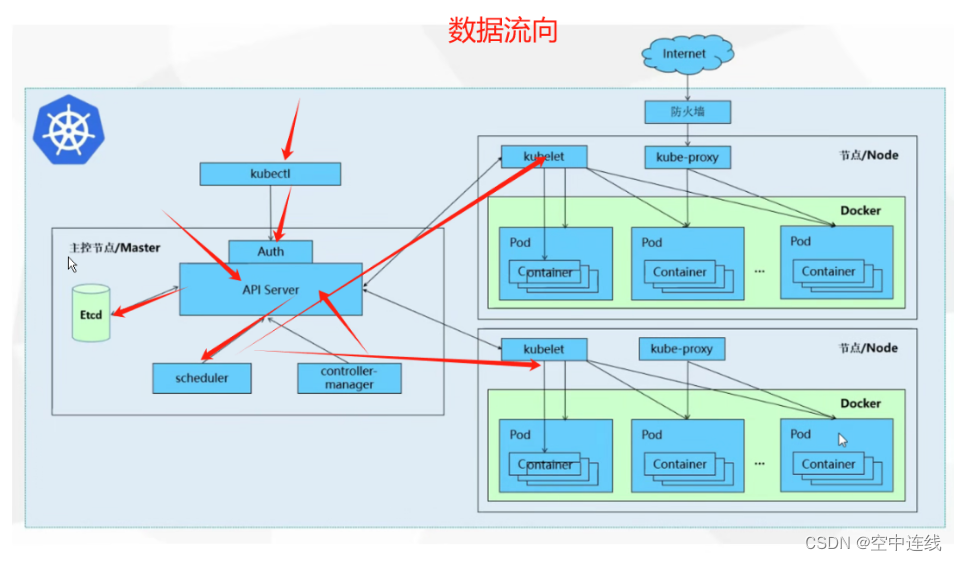
kubernate 基本概念
一 K8S 是什么? K8S 全称:Kubernetes 1 kubernate基本概念 作用: 用于自动部署、扩展和管理“容器化(containerized)应用程序”的开源系统。 可以理解成 K8S 是负责自动化运维管理多个容器化程序(比如…...
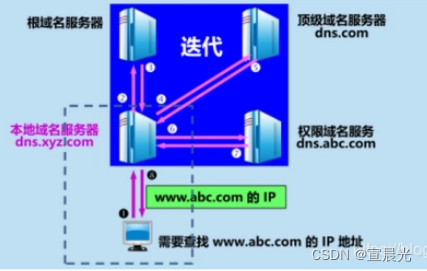
【系统架构师】-选择题(十二)计算机网络
1、网闸的作用:实现内网与互联网通信,但内网与互联网不是直连的 2、管理距离是指一种路由协议的路由可信度。15表示该路由信息比较可靠 管理距离越小,它的优先级就越高,也就是可信度越高。 0是最可信赖的,而255则意味…...

代码随想录|总结篇
完结篇: 60天,还是坚持了下来,达成算法路上的一个小目标。 加入代码随想录训练营之前,也断断续续刷到了树那一章节,但后面因为导师项目等种种情况,一直耽搁到年后。年后打算重新开始刷题时,正好…...

网络编程套接字和传输层tcp,udp协议
认识端口号 我们知道在网络数据传输的时候,在IP数据包头部有两个IP地址,分别叫做源IP地址和目的IP地址。IP地址是帮助我们在网络中确定最终发送的主机,但是实际上数据应该发送到主机上指定的进程上的,所以我们不仅要确定主机&…...

通过wget下载ftp文件
通过wget下载ftp文件 基础用法带密码的http文件带密码的ftp文件补充 基础用法 在下载的过程中会显示进度条,包含百分比,已下载字节,下载速度,剩余时间。 # 下载单个文件 wget [url_file]# 下载目录全部文件 wget [url_dir/*] wg…...

Acrobat Pro DC 2023 for Mac:PDF处理的终极解决方案
Acrobat Pro DC 2023 for Mac为Mac用户提供了PDF处理的终极解决方案。它具备强大的文档处理能力,无论是查看、编辑还是创建PDF文件,都能轻松胜任。在编辑功能方面,Acrobat Pro DC 2023支持对文本、图像进行精准的修改和调整,还能添…...

map容器
目录 map构造和赋值 map大小和交换 map插入和删除 map查找和统计 map排序 map构造和赋值 map中所有元素都是pair(即一对) pair中第一个元素为key(键值),起到索引作用,第二个元素为value(…...

GNU/Linux - 是否可以多次打开同一个设备文件
使用设备/dev/ttyS1举例来说明。 一个设备文件打开多次 在 Linux 中,多次打开 /dev/ttyS1 以读取数据通常是可以接受的。多次打开 /dev/ttyS1 并向 /dev/ttyS1 发送数据时,所有打开的文件描述符都能接收数据。每个打开的文件描述符都代表与串行端口的独立…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
