P1443 马的遍历
题目描述:
有一个 𝑛×𝑚n×m 的棋盘,在某个点 (𝑥,𝑦)(x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。
代码:
package lanqiao;import java.util.*;public class Main {static int n,m,x,y;static int[][] a = new int[410][410];static int[] aa = new int[] {2, 1, 2, -1, -2, -1, -2, 1};static int[] bb = new int[] {1, 2, -1, -2, -1, 2, 1, -2};public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();m = sc.nextInt();x = sc.nextInt();y = sc.nextInt();//初始化数组for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){a[i][j] = -1;}}dfs(x,y,0);a[x][y] = 0;for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){System.out.printf("%-5d", a[i][j]);}System.out.println();}}public static void dfs(int x,int y,int t){if(t >200) //DFS不加剪枝的话需要加阙值{return;}a[x][y] = t;for(int i = 0;i < 8;i ++){if(x + aa[i] >= 1 && y + bb[i] >= 1 && x + aa[i] <= n && y + bb[i] <= m&& (a[x + aa[i]][y + bb[i]] == -1 || a[x + aa[i]][y + bb[i]] > t + 1))//需要对未走过的格子,或者新路线步数较短的格子进行重新赋值{dfs(x + aa[i],y + bb[i],t + 1);}}}
}相关文章:

P1443 马的遍历
题目描述: 有一个 𝑛𝑚nm 的棋盘,在某个点 (𝑥,𝑦)(x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。 代码: package lanqiao;import java.util.*;public class Main {static int n,m…...

AI学习指南概率论篇-贝叶斯推断
AI学习指南概率论篇-贝叶斯推断 概述 在人工智能中,贝叶斯推断是一种基于贝叶斯统计理论的推理方法。它通过使用概率论的知识,结合先验信息和观测数据,来更新对未知变量的推断。贝叶斯推断提供了一种合理的方法来处理不确定性,并…...

大数据测试
1、前言 大数据测试是对大数据应用程序的测试过程,以确保大数据应用程序的所有功能按预期工作。大数据测试的目标是确保大数据系统在保持性能和安全性的同时,平稳无差错地运行。 大数据是无法使用传统计算技术处理的大型数据集的集合。这些数据集的测试涉…...
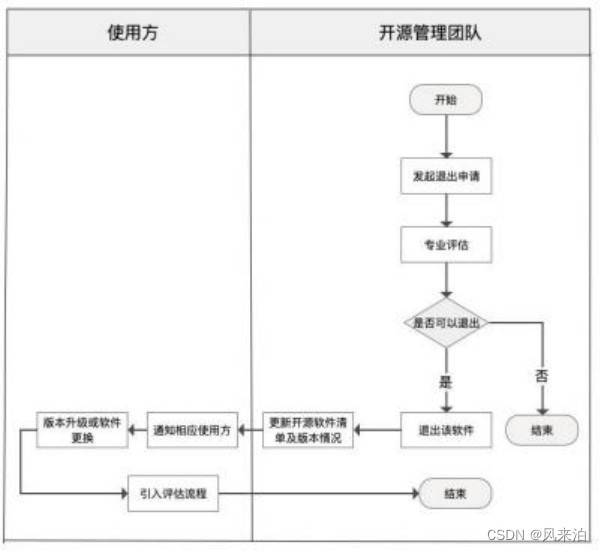
金融业开源软件应用 管理指南
金融业开源软件应用 管理指南 1 范围 本文件提供了金融机构在应用开源软件时的全流程管理指南,对开源软件的使用和管理提供了配套 组织架构、配套管理规章制度、生命周期流程管理、风险管理、存量管理、工具化管理等方面的指导。 本文件适用于金融机构规范自身对开…...

SolidWorks 齿轮配合
SolidWorks 齿轮配合 在SolidWorks中,齿轮配合是一种特殊的配合类型,用于模拟两个或多个齿轮之间的旋转关系。这种配合确保当一个齿轮旋转时,其他齿轮按照特定的比例旋转,非常适合模拟机械传动系统。以下是使用齿轮配合的详细步骤…...

鸿蒙开发-ArkTS语言-XML
鸿蒙开发-UI-web 鸿蒙开发-UI-web-页面 鸿蒙开发-ArkTS语言-基础类库 鸿蒙开发-ArkTS语言-并发 鸿蒙开发-ArkTS语言-并发-案例 鸿蒙开发-ArkTS语言-容器 鸿蒙开发-ArkTS语言-非线性容器 文章目录 前言 一、XML概述 二、XML生成 三、XML解析 1.解析XML标签和标签值 2.解析XML属性…...

网安面经之文件上传漏洞
一、文件上传漏洞 1、文件上传漏洞的原理?危害?修复? 原理:⽂件上传漏洞是发⽣在有上传功能的应⽤中,如果应⽤程序对⽤户上传的⽂件没有控制或者存在缺陷,攻击者可以利⽤应⽤上传功能存在的缺陷ÿ…...
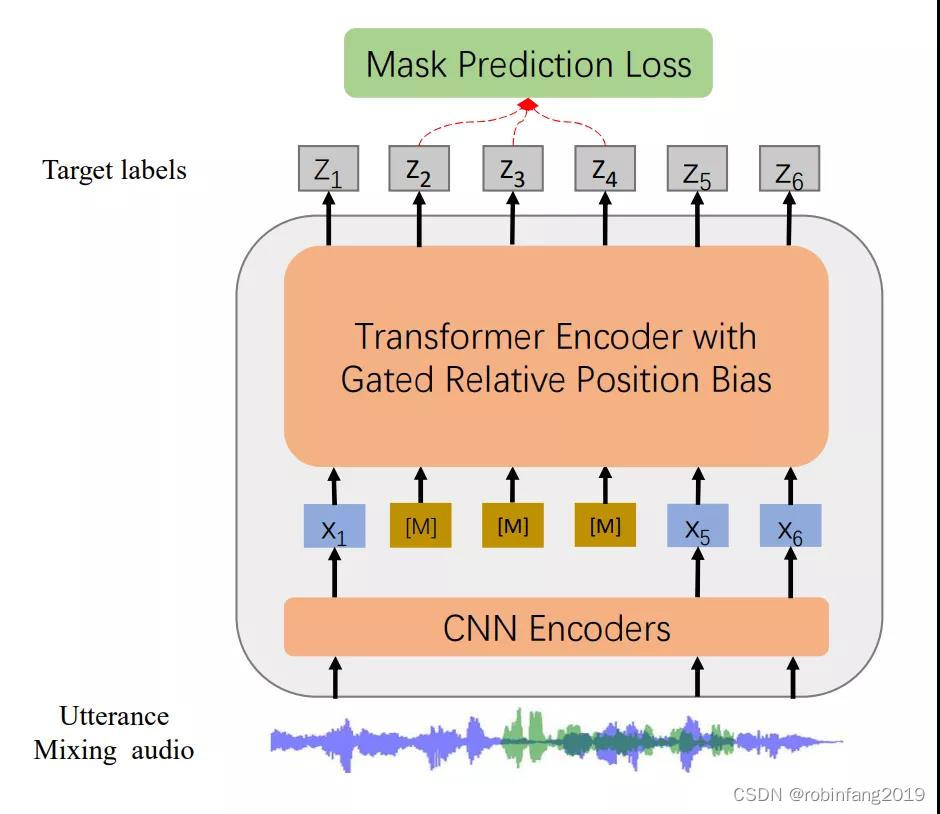
如何使用 WavLM音频合成模型
微软亚洲研究院与 Azure 语音组的研究员们提出了通用语音预训练模型 WavLM。通过 Denoising Masked Speech Modeling 框架(核心思想是通过预测被掩蔽(即遮蔽或删除)的语音部分来训练模型,同时还包括去噪的过程)&#x…...

学习java第六十七天
注入 Bean 的注解有哪些? 答: Autowired:根据类型进行注入,如果匹配到多个Bean,则会爆出异常。可以和Qualifier搭配使用,指定使用哪个名称的Bean Resource:首先根据名称注入,如果…...

Linux(Ubuntu24.04) 安装 MinIO
本文所使用的 Ubuntu 系统版本是 Ubuntu 24.04 ! # 1、下载 MinIO wget https://dl.min.io/server/minio/release/linux-amd64/minio# 2、添加可执行权限 chmod x minio# 3、导出环境变量,用于设置账号密码,我设置的账号和密码都是 minioadmin export MI…...
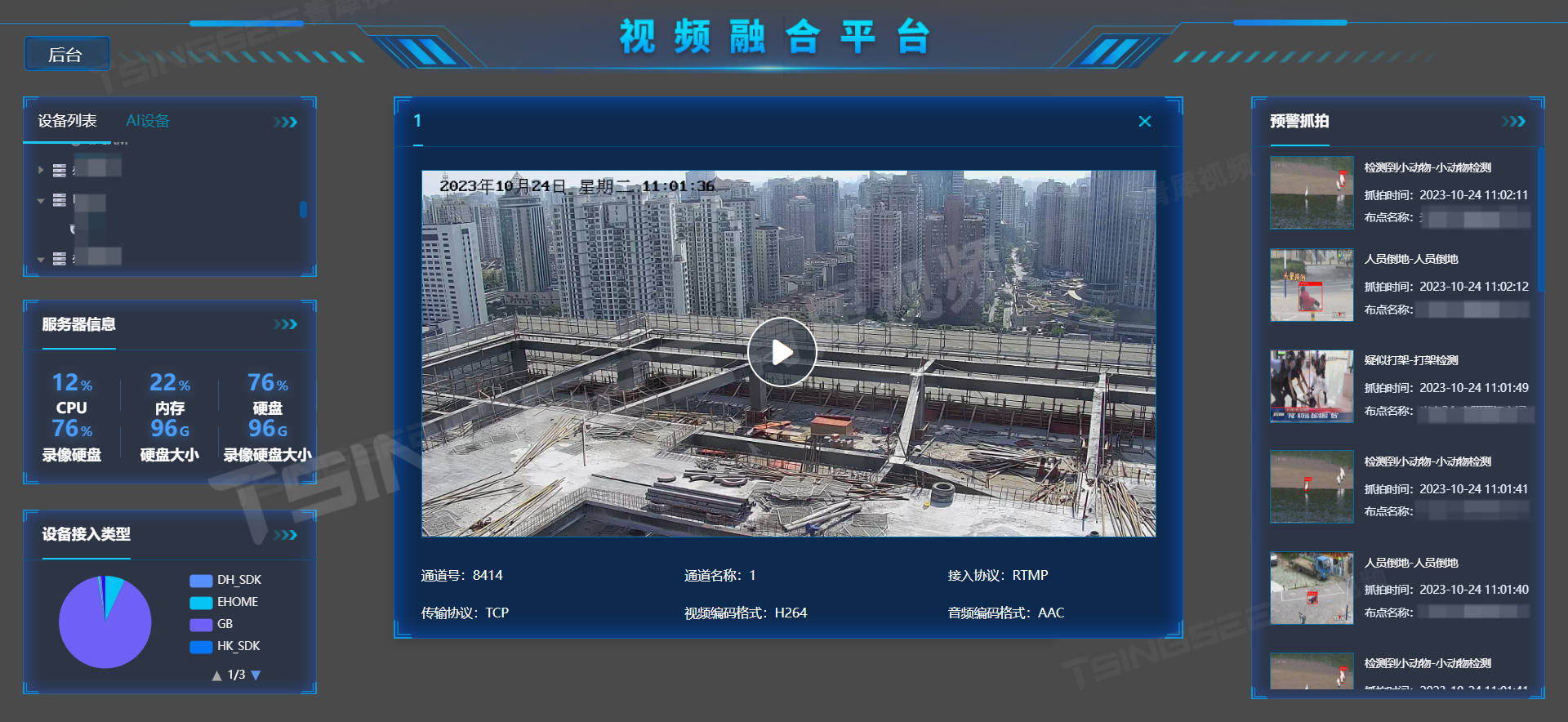
视频汇聚边缘网关EasyCVR硬件设备无法访问域名,解析失败该如何处理?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。视频汇聚融合管理平台EasyCVR既具备传统安防视…...
差速机器人模型LQR 控制仿真(c++ opencv显示)
1 差速机器人状态方程构建 1.1差速机器人运动学模型 1.2模型线性化 1.3模型离散化 2离散LQR迭代计算 注意1:P值的初值为Q。见链接中的: 注意2:Q, R参数调节 注意3:LQR一般只做横向控制,不做纵向控制。LQR输出的速度…...

探索设计模式的魅力:权力集中,效率提升,中心化模式的优势与挑战
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》 💪🏻 制定明确可量化的目标,坚持默默的做事。 ✨欢迎加入探索中心化模式之旅✨ 大家好啊!👋 这次我们要聊的是IT界一…...
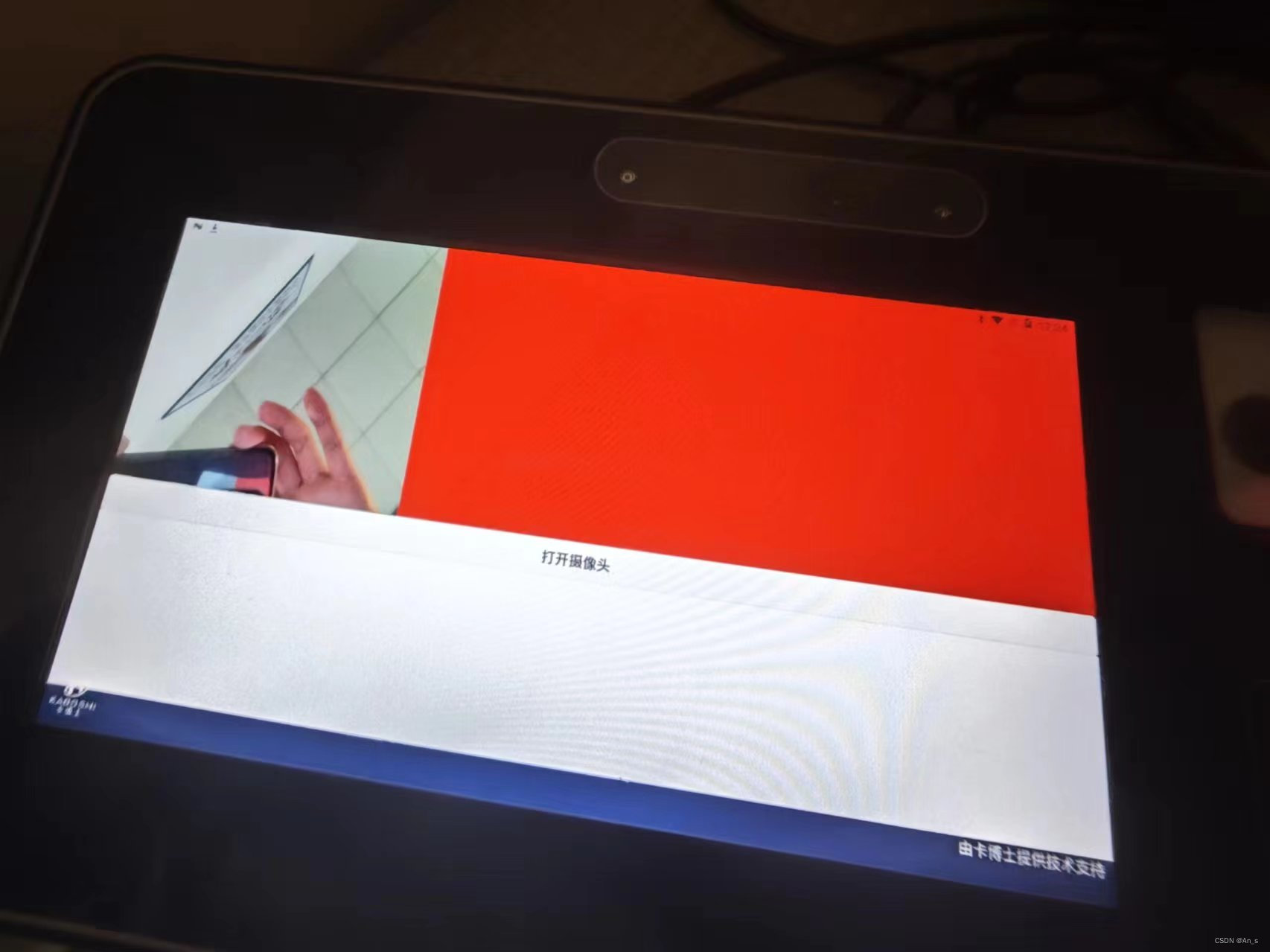
uniapp0基础编写安卓原生插件之编写安卓页面在uniapp上显示(摄像头调用)
前言 如果你对安卓插件开发部分不熟悉你可以先看uniapp0基础编写安卓原生插件和调用第三方jar包和编写语音播报插件之零基础编写安卓插件 效果 开始 dcloud_uniplugins.json {"nativePlugins": [{"hooksClass": "","plugins": [{&…...

fastapi数据库连接池的模版
在FastAPI中,数据库连接池通常通过使用SQLAlchemy来实现。以下是一些基于官方文档和其他可靠资源的数据库连接池模板示例。 1. 使用SQLAlchemy创建异步数据库引擎 首先,你需要创建一个异步数据库引擎,这将作为数据库连接的来源。以下是使用sqlalchemy.ext.asyncio模块创建…...
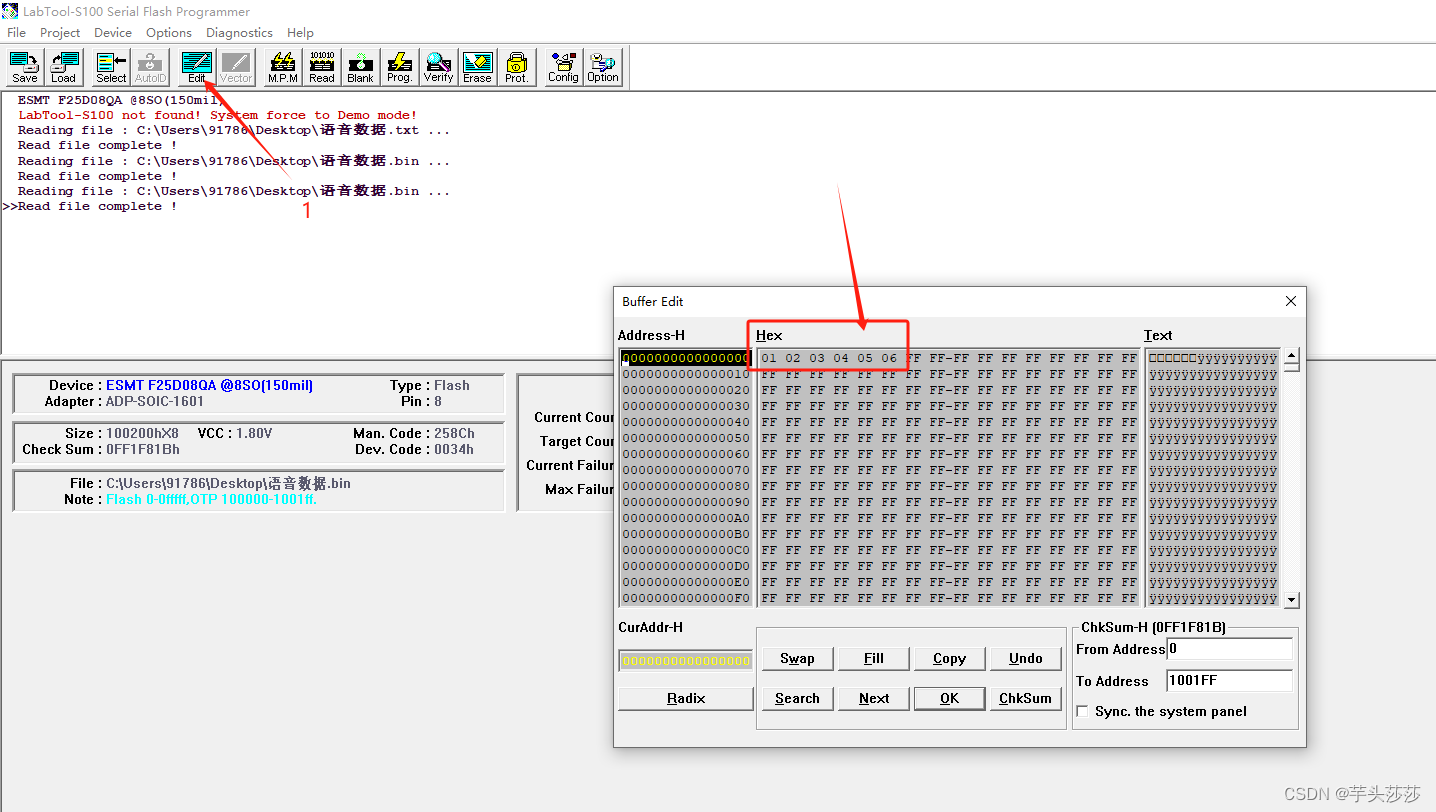
如何批量将十六进制数据转成bin文件
最近在做新项目遇到一个问题,我们要通过上位机把一堆数据通过串口发送给下位机存储,而上位机需要Bin文件。 解决办法: 1)创建一个记事本文件,然后将其后缀修改成.bin 2)然后打开notepad,新建一个文件,随便写下数据 我…...

知识付费程序源码_30秒轻松搭建知识付费小程序_免费试用,知识付费工具有哪些?哪个比较好用?
继2016年知识付费大火之后,衍生出很多关于知识付费的平台或工具。除了得到APP、荔枝微课、千聊等需要用户作为“客”家申请入驻的流量型平台,还有一些其他的知识付费工具,那么有哪些呢? 知识付费工具,推荐使用系统。 自2016年知识…...
容器化、CDN与微服务)
【系统架构师】-案例篇(九)容器化、CDN与微服务
某汽车制造企业提出开发一个车联网系统。该系统釆用微服务架构,将系统功能分解为多个松散耦合且可独立部署的较小组件或服务。最终设计的系统包括了车辆信息服务、车辆监控服务、车辆控制服务、人车授权服务、资源聚合服务、车机互联服务等。 在系统上线之后&#…...

OpenAI工作原理及核心机制
一、工作原理: 1、数据收集: AI系统首先需要大量的数据作为学习的基础。这些数据可以是文本、图像、音频、视频等形式,来源于互联网、传感器、数据库等渠道。 2、预处理: 收集到的数据需要经过清洗和整理,去除无关…...
JVM调优-调优原则和原理分析
1.写在前面 对于JVM调优这个话题,可能大部分程序员都听过这个名词。 但是绝大多数程序员,都没有真真实实去干过,都没有真实的实践过。也不懂得如何调优?不知道要调成怎么样? 那今天咋们就对这个话题来展开描述一下&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

大模型——基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程
基于Docker+DeepSeek+Dify :搭建企业级本地私有化知识库超详细教程 下载安装Docker Docker官网:https://www.docker.com/ 自定义Docker安装路径 Docker默认安装在C盘,大小大概2.9G,做这行最忌讳的就是安装软件全装C盘,所以我调整了下安装路径。 新建安装目录:E:\MyS…...
