机器学习作业4——朴素贝叶斯分类器
目录
一、理论
一个例子:
二、代码
对于代码的解释:
1.fit函数:
2.predict函数:
三、实验结果
原因分析:
一、理论
朴素贝叶斯分类器基于贝叶斯定理进行分类,通过后验概率来判断将新数据归为哪一类。通过利用贝叶斯定理计算后验概率,并选择具有最高后验概率的类别作为预测结果,朴素贝叶斯分类器能够在考虑了先验概率和观察到的数据特征后,做出基于统计推断的分类决策,从而实现有效的分类。
步骤:
1.计算先验概率:先验概率表示了在没有任何其他信息的情况下,一个数据点属于每个类别的概率。
2.计算条件概率:条件概率表示了在给定某一类别的情况下,某个特征取某个值的概率。
3.计算后验概率:当有一个新的数据点需要分类时,朴素贝叶斯根据该数据点的特征值,利用贝叶斯定理计算每个类别的后验概率。后验概率表示了在考虑了新的观察结果后,每个类别的概率。
4.做出分类:根据计算得到的后验概率,选择具有最高后验概率的类别作为预测结果。
先验概率:
其中:ck是类别,D是数据数量,Dck是类别为ck的数据数量。
条件概率:
其中:Xi代表第i个特征,ai,j代表第i个特征中第j个类型,代表在类别为ck时,在第i个特征中的第j个类型的数量。
后验概率:
因为我们只需要分类,因为不同后验概率分母都相同,所以可以把分母去掉,只需要比较分子的大小即可,即:
其中:代表当前测试数据的每个类型为xi,在ck类别下的条件概率的连乘积。
可以看到公式简洁了不少。
一个例子:
假设数据集:
| 特征1 | 特征2 | 类别 |
|---|---|---|
| 1 | 1 | A |
| 1 | 0 | A |
| 0 | 1 | B |
| 0 | 1 | A |
| 1 | 0 | B |
现在预测一个特征1为1,特证2为1的测试元组是什么类别。
首先计算类别的先验概率和所有条件概率:
P(A)= 3/5,P(B)= 2/5
对于特征1:
P1(1∣A)= 2/3,P1(1 | B)= 1/2,
对于特征2:
P2(1 | A) = 2/3,P2(1 | B) = 1/2
然后计算预测为A和B的后验概率,并比较大小,得出结果
P(A|X) = P(A)*P1(1∣A)*P2(1 | A) = 4/15
P(B|X) = P(B)*P1(1 | B)*P2(1 | B) = 1/10
可以看到P(A|X)比较大,所以是A类
二、代码
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score class NaiveBayesClassifier:def __init__(self):self.class_prior = {} # 存储类别的先验概率self.feature_prob = {} # 存储特征在各个类别下的条件概率def fit(self, X, y):n_samples, n_features = X.shape # 获取样本数和特征数self.classes = np.unique(y) # 获取目标标签中的唯一类别值print("计算先验概率:")for c in self.classes:# 统计每个类别在目标标签中的出现次数,并除以样本总数,得到先验概率self.class_prior[c] = np.sum(y == c) / n_samplesprint("先验概率: 类别, 概率 "+repr(c)+" "+repr(self.class_prior[c]))# 外层循坏遍历类别,内层循环遍历每个特征,内层循环每次要计算出每个特征下不同取值的在当前类别下的条件概率,存放到[c][feature_index]下print("计算条件概率:")for c in self.classes:self.feature_prob[c] = {} # 初始化存储特征条件概率的字典for feature_index in range(n_features):# 对于每个特征,统计在当前类别下的取值及其出现次数,并除以总次数,得到条件概率# values是feature_index列中不同的取值,counts是这些不同取值的个数(在类别为C下的)values, counts = np.unique(X[y == c, feature_index], return_counts=True)self.feature_prob[c][feature_index] = dict(zip(values, counts / np.sum(counts)))#dict是变为以values和counts/np.sum的字典,zip就是一个方便的操作for i in range(len(counts)):print("条件概率:P(" + repr(values[i]) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][values[i]]))def predict(self, X):predictions = [] # 存储预测结果的列表#对于测试集中的每个元素cnt = 0for x in X:print("\n对于第" + repr(cnt) + "个测试集:")cnt+=1max_posterior_prob = -1 # 最大后验概率初始化为-1predicted_class = None # 预测类别初始化为空#对于每个类别for c in self.classes:# 计算后验概率,先验概率乘以各个特征的条件概率posterior_prob = self.class_prior[c]print("对于类别"+repr(c)+" = "+"[先验"+repr(self.class_prior[c])+"]", end = '')#对于每个特征for feature_index, feature_value in enumerate(x):if feature_value in self.feature_prob[c][feature_index]:print(" * [P("+ repr(feature_value) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][feature_value]) + "]", end = '')posterior_prob *= self.feature_prob[c][feature_index][feature_value]else:print(" * 1")# 更新预测值print(" = " + repr(posterior_prob))if posterior_prob > max_posterior_prob:max_posterior_prob = posterior_probpredicted_class = cpredictions.append(predicted_class) # 将预测结果添加到列表中return predictions # 返回预测结果列表data = {'outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'rain', 'overcast', 'overcast', 'rain'],'temperature': ['hot', 'hot', 'hot', 'mild', 'cool', 'cool', 'cool', 'mild', 'cool', 'mild', 'mild', 'mild', 'hot', 'mid'],'humidity': ['high', 'high', 'high', 'high', 'normal', 'normal', 'normal', 'high', 'normal', 'normal', 'normal', 'high', 'normal', 'high'],'wind': ['weak', 'strong', 'weak', 'weak', 'weak', 'strong', 'strong', 'weak', 'weak', 'weak', 'strong', 'strong', 'weak', 'strong'],'playtennis': ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
}
#创建DataFrame
df = pd.DataFrame(data)
X = df.drop('playtennis', axis=1)#axis=1删除列,=0删除行
y = df['playtennis']# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3)
X_train = X_train.values#化为二维数组,便于遍历
X_test = X_test.values
y_train = y_train.values
y_test = y_test.valuesprint("训练集:")
for i in range(len(y_train)):print(repr(i)+": "+repr(X_train[i])+" "+repr(y_train[i]))
print("测试集:")
for i in range(len(y_test)):print(repr(i)+": "+repr(X_test[i])+" "+repr(y_test[i]))nb_classifier = NaiveBayesClassifier()
nb_classifier.fit(X_train, y_train)y_pred = nb_classifier.predict(X_test)
print("预测结果:")
for i in range(len(y_pred)):print(repr(i)+"正确,预测: "+repr(y_test[i])+", "+repr(y_pred[i]))accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, pos_label='yes')
recall = recall_score(y_test, y_pred, pos_label='yes')
f1 = f1_score(y_test, y_pred, pos_label='yes')
print("准确率:", accuracy)
print("精确率:", precision)
print("召回率:", recall)
print("f1:", f1)
对于重要代码的解释:
1.fit函数:
训练测试集的主要代码,先把训练集中所有的条件概率和先验概率算出来,在后面的预测中会使用到。
先验概率:
print("计算先验概率:")for c in self.classes:# 统计每个类别在目标标签中的出现次数,并除以样本总数,得到先验概率self.class_prior[c] = np.sum(y == c) / n_samplesprint("先验概率: 类别, 概率 "+repr(c)+" "+repr(self.class_prior[c]))所有条件概率:
print("计算条件概率:")for c in self.classes:self.feature_prob[c] = {} # 初始化存储特征条件概率的字典for feature_index in range(n_features):# 对于每个特征,统计在当前类别下的取值及其出现次数,并除以总次数,得到条件概率# values是feature_index列中不同的取值,counts是这些不同取值的个数(在类别为C下的)values, counts = np.unique(X[y == c, feature_index], return_counts=True)self.feature_prob[c][feature_index] = dict(zip(values, counts / np.sum(counts)))for i in range(len(counts)):print("条件概率:P(" + repr(values[i]) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][values[i]]))
结果:
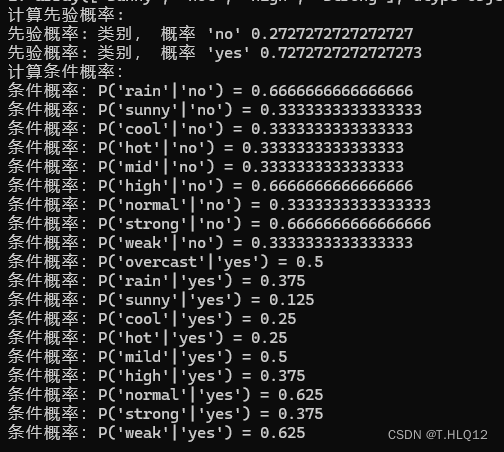
2.predict函数:
这个函数用于测试集的预测,对于测试集中的每个元组,都要对于所有类别,计算一次该类别下的后验概率,然后选择所有类别中后验概率最大的,作为预测结果,而每个后验概率,通过该元组下的每个特征下的类型对应的条件概率的累乘和该类别的先验概率的乘积来确定。
对于每个元组:
for x in X:print("\n对于第" + repr(cnt) + "个测试集:")cnt+=1max_posterior_prob = -1 # 最大后验概率初始化为-1predicted_class = None # 预测类别初始化为空对于每个类别:
for c in self.classes:posterior_prob = self.class_prior[c]对于每个特征:
for feature_index, feature_value in enumerate(x):if feature_value in self.feature_prob[c][feature_index]:print(" * [P("+ repr(feature_value) + "|" + repr(c) + ") = " + repr(self.feature_prob[c][feature_index][feature_value]) + "]", end = '')posterior_prob *= self.feature_prob[c][feature_index][feature_value]else:print(" * 1")每次计算完后,维护最大值以及类型:
if posterior_prob > max_posterior_prob:max_posterior_prob = posterior_probpredicted_class = c每个元组计算完后,添加到预测数组中,最后返回预测数组即可。
三、实验结果
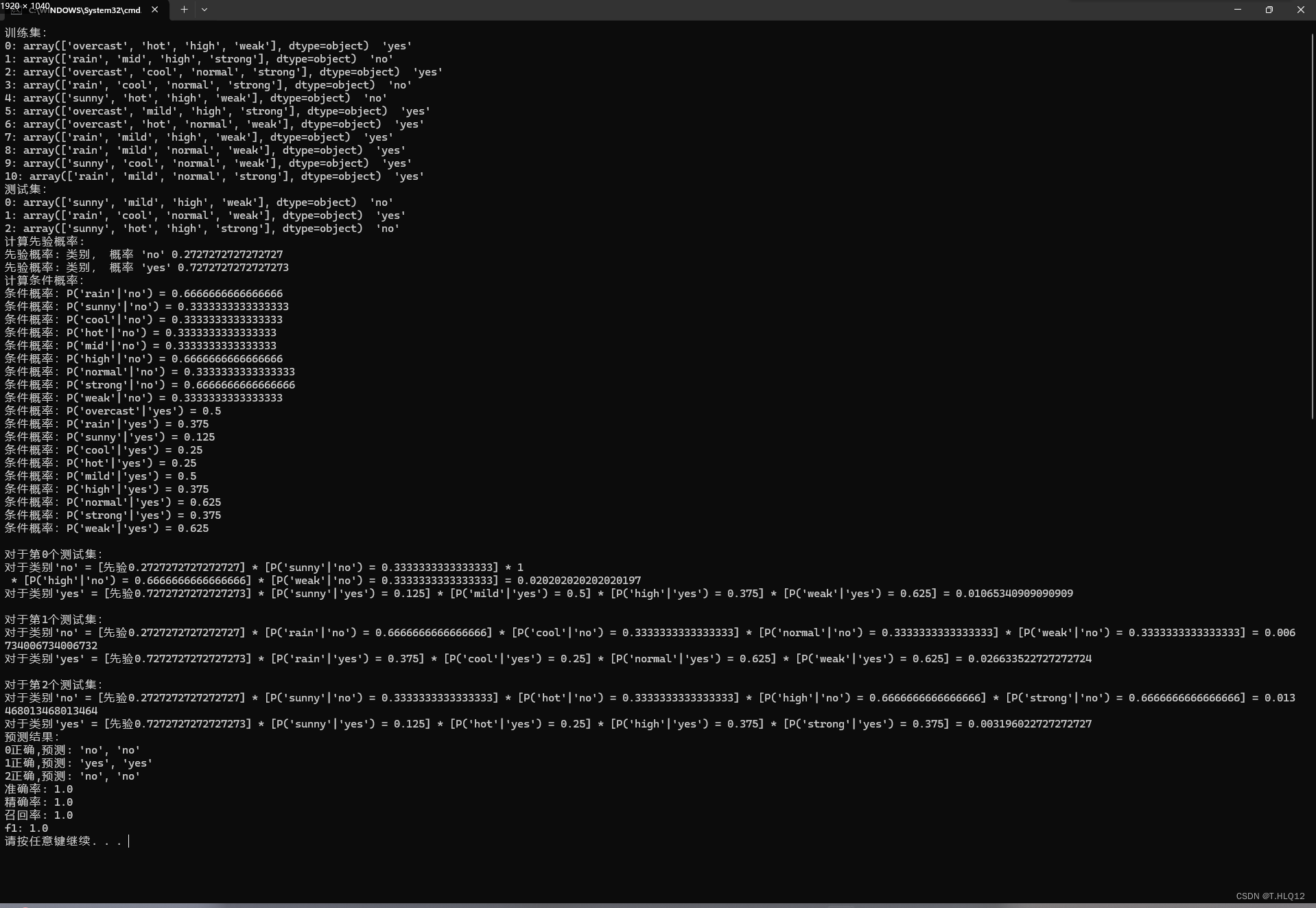
上图是最好的一个实验结果,所有指标为1,其他的实验结果准确率较低
原因分析:
这个训练集数据过小,但是特征和每个特征中的类型又比较多,再加上测试集一共就13条,数据使用不同的随机种子会使得一些测试集中的特征在不同类别下的条件概率没有出现过,因为没有出现过,直接就不处理这个特征了,就容易出现误差。
例如:
当随机种子为1时:

当随机种子为4时:

朴素贝叶斯分类器优缺点分析:
优点:
-
适用广:朴素贝叶斯算法在处理大规模数据时表现良好,适用于许多实际问题。
-
对小规模数据表现良好:即使在小规模数据集上,朴素贝叶斯分类器也能有好的结果。
-
对缺失数据不敏感:朴素贝叶斯算法对缺失数据不敏感,即使有部分特征缺失或者未出现,仍然可以有效地进行分类。
缺点:
-
假设过于简化:朴素贝叶斯假设特征之间相互独立,在现实中,数据一般难以是真正独立的,因此会导致结果不准确。
-
处理连续性特征较差:朴素贝叶斯算法通常假设特征是离散的,对于连续性特征的处理不够灵活,可能会影响分类性能。
相关文章:

机器学习作业4——朴素贝叶斯分类器
目录 一、理论 一个例子: 二、代码 对于代码的解释: 1.fit函数: 2.predict函数: 三、实验结果 原因分析: 一、理论 朴素贝叶斯分类器基于贝叶斯定理进行分类,通过后验概率来判断将新数据归为哪一类。通过利用贝…...
BUU-[GXYCTF2019]Ping Ping Ping
考察点 命令执行 题目 解题 简单测试 ?ip应该是一个提示,那么就测试一下?ip127.0.0.1 http://0c02a46a-5ac2-45f5-99da-3d1b0b951307.node4.buuoj.cn:81/?ip127.0.0.1发现正常回显 列出文件 那么猜测一下可能会有命令执行漏洞,测试?ip127.0.…...
代码随想录Day 41|Leetcode|Python|198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III
198.打家劫舍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个…...
【吴恩达机器学习-week2】多个变量的特征缩放和学习率问题
特征缩放和学习率(多变量) 目标 利用上一个实验中开发的多变量例程在具有多个特征的数据集上运行梯度下降探索学习率对梯度下降的影响通过 Z 分数归一化进行特征缩放,提高梯度下降的性能 import numpy as np np.set_printoptions(precisio…...

C#字符串的拼接
在C#中有多种拼接字符串的方式,今天小编就分享一些比较常用的。 方法1 string str "123"; str str "456"; 运行结果: "123456" 方法2 字符串与数字拼接 会将数字默认为字符串进行拼接 string str "123"; str str 1;…...

哈希表Hash table
哈希表是根据关键码的值而直接进行访问的数据结构。 数组就是⼀张哈希表。 哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素,如下图所示: 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断⼀个元素是…...

jdk8新特性----Lambda表达式
一、介绍 1、简介 Java的Lambda表达式是Java 8引入的一个特性,它支持函数式编程,允许将函数作为方法的参数或返回值,从而简化了匿名内部类的使用,并提供了对并行编程的更好支持。 2、语法 Lambda表达式的使用前提是存在一…...
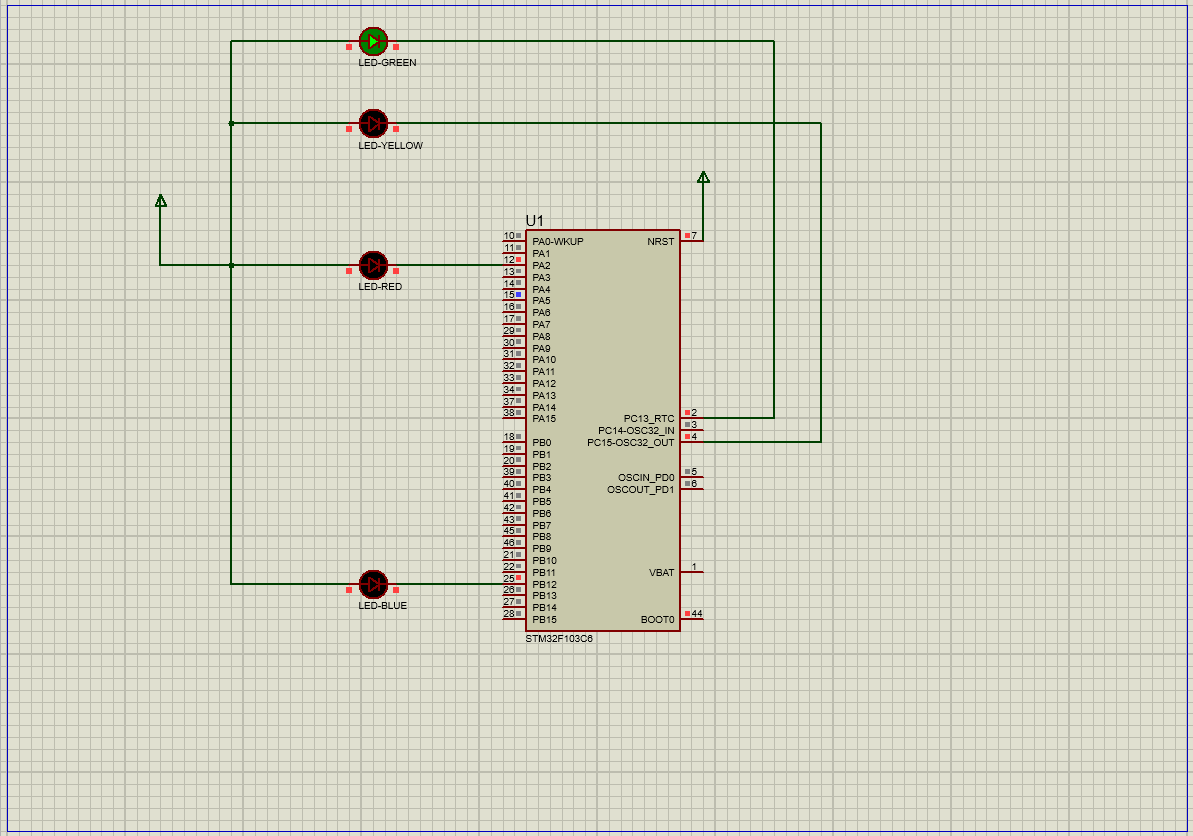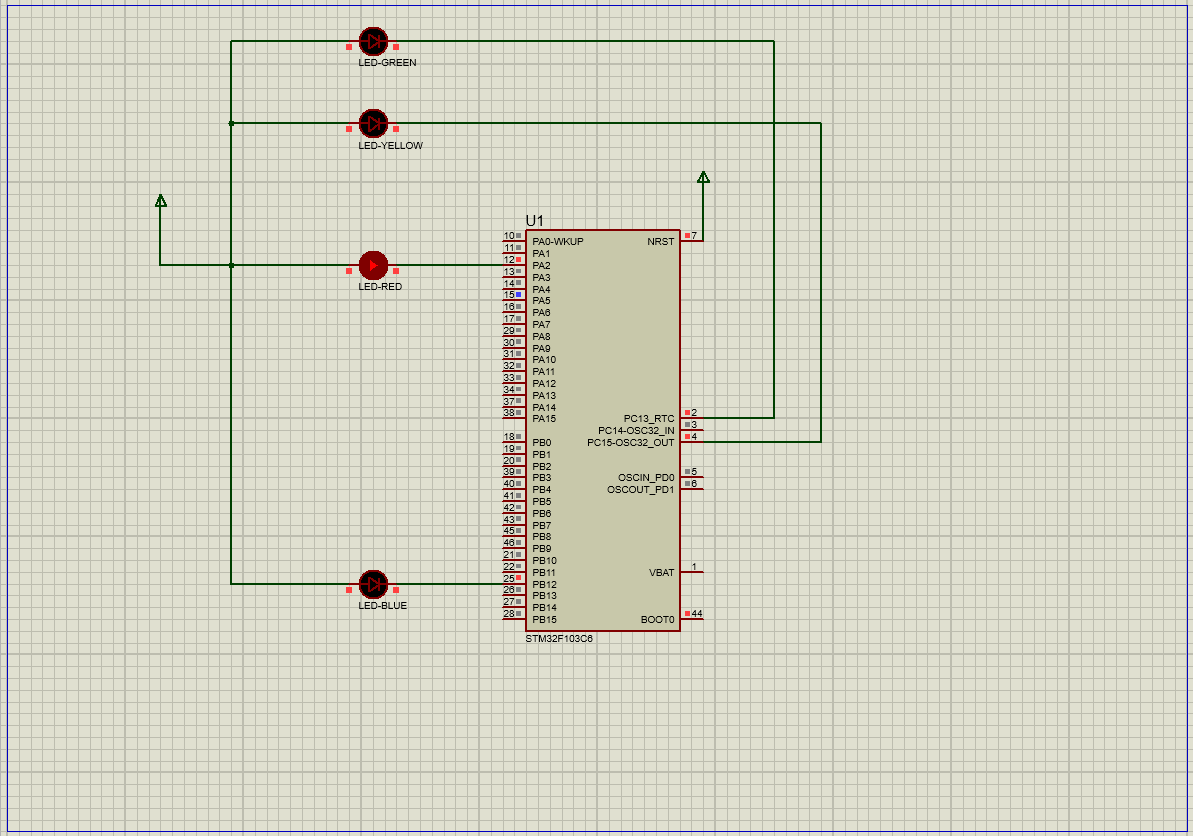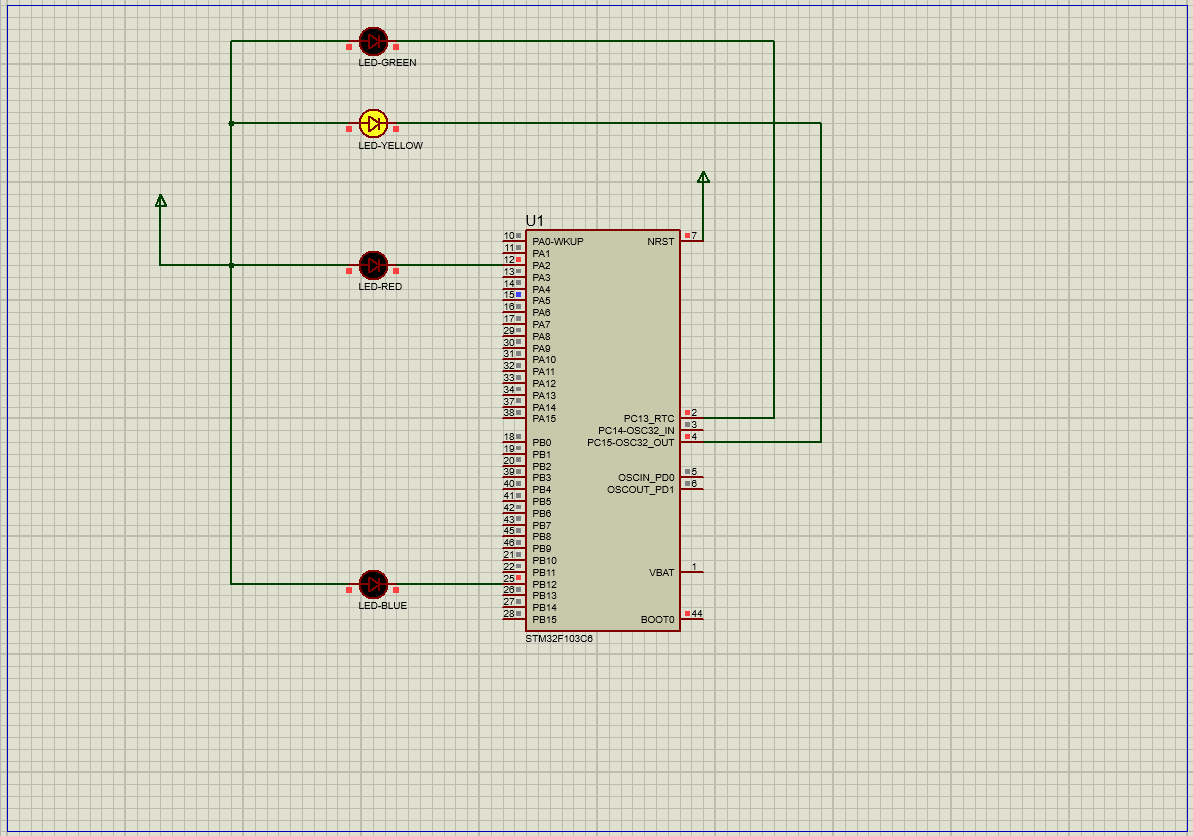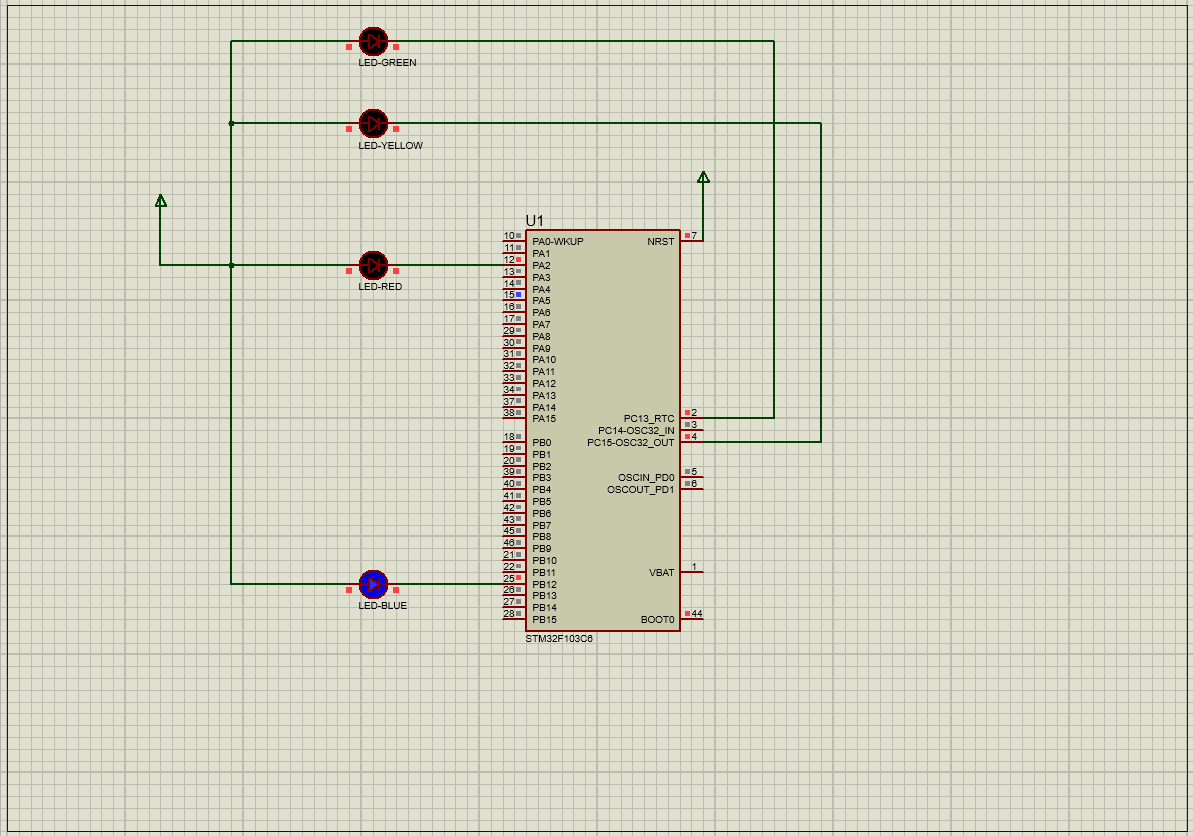
在STM32中用寄存器方式点亮流水灯
文章目录 实验资料一、对寄存器的理解1.通俗认识寄存器2.深入了解寄存器(1)端口配置低寄存器(配置0到7引脚的寄存器)(2)端口配置高寄存器(配置8到15引脚) 3.GPIO口的功能描述 二、配…...
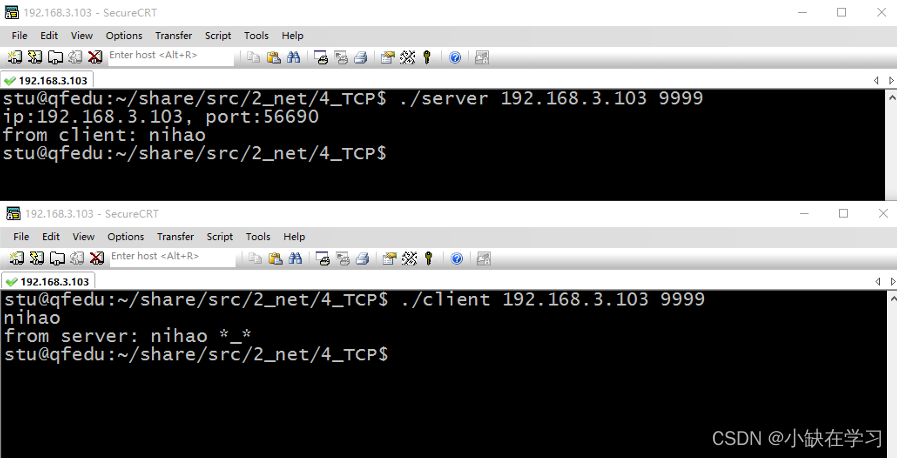
TCP(TCP客户端、服务器如何通信)
一、TCP介绍 TCP的特点: 面向连接的协议:TCP是一种可靠的、面向连接的协议,在通信之前需要建立连接,以确保数据的可靠传输。这意味着在传输数据之前,发送方和接收方之间需要建立一条可靠的连接通道。流式协议&#x…...
)
pdf 文件版面分析--PyMuPDF (python 文档解析提取)
1.介绍 PyMuPDF 和Fitz 是用于Python中处理PDF文件的相关模块。Fitz是P有MuPDF的字模块。提供一个简化和封装版本的P有MuPDF功能。 关系: PyMuPDF: 提供广泛的功能,用于操作PDF文档, 包括方便的高级函数与底层操作Fitz &#x…...

sql update 多表关联 inner join
当您需要更新一个表或者多个表中的数据,而多个表又存在关联时,可以使用 INNER JOIN 子句将多个表关联起来,并使用 SET更新。 格式如下: UPDATE table1 INNER JOIN table2 ON table1.column1 table2.column1 SET table1.column2…...

【OceanBase诊断调优】—— 租户资源统计项及其查询方法
本文主要介绍 OceanBase 数据库中租户资源统计项及其查询方法。 适用版本 OceanBase 数据库 V4.1.x、V4.2.x 版本。 CPU 资源统计项 逻辑 CPU 使用率(线程处理请求的时间占比)。 通过虚拟表 __all_virtual_sysstat 在 SYS 系统租户下,查看…...

【一键录音,轻松转换:用Python打造个性化音频记录工具】
在数字化时代,音频记录已成为日常学习、工作和娱乐不可或缺的一部分。想象一下,只需简单按下几个键,即可随时随地捕捉灵感,记录会议要点,或是珍藏孩子的童言稚语。本文将引领您步入Python编程的奇妙世界,展示如何借助几个强大的库,构建一个既简单又实用的音频录制及转换…...

Java类与对象(一)
类的定义与使用 在Java中使用关键字class定义一个类,格式如下: class 类名{// 成员变量/字段/属性//成员方法/行为 }Java中类和c语言中的结构体有点类似, 在Java中类名一般采用大驼峰(每个首字母大写)的形式…...

python中的装饰器,例子说明
在Python中,嵌套装饰器是指在一个函数上应用多个装饰器。每个装饰器都可以为函数添加一些特定的功能。以下是一个稍微复杂一些的例子,我们将创建一个记录日志和验证权限的嵌套装饰器。 ### 例子:记录日志和权限验证的嵌套装饰器 假设我们正…...

Leetcode经典题目之用队列实现栈
P. S.:以下代码均在VS2019环境下测试,不代表所有编译器均可通过。 P. S.:测试代码均未展示头文件stdio.h的声明,使用时请自行添加。 目录 1、题目展示2、题目分析3、完整代码演示4、结语 1、题目展示 前面我们了解过如何实现队列…...

DBSCAN聚类算法
目录 背景DBSCAN算法DBSCAN算法原理DBSCAN算法基本步骤DBSCAN算法调优DBSCAN算法优缺点参考文献 背景 如果有车队在某一片区域经常规律性作业,现在要让你来绘制这一片的路网,你会选择让一辆车从头到尾把所有路网跑一遍还是基于历史轨迹点通过技术手段构…...

【tauri】安装
https://blog.csdn.net/freewebsys/article/details/136092092 1 安装nodejs curl -sL https://deb.nodesource.com/setup_18.x -o nodesource_setup.sh sudo bash nodesource_setup.sh sudo apt install nodejs # 查看版本 node -v2 安装webkit2 sudo apt update sudo apt i…...

(Java)心得:LeetCode——19.删除链表的倒数第 N 个节点
一、原题 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
树莓派安装opencv
安装opencv 上述步骤完成后,输入以下代码(基于python3) sudo apt-get install python3-opencv -y不行的话,试试换源,然后 sudo apt-get update成功! 测试opencv是否安装成功 输入 python3 然后再输入 import cv2 没有报错就…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
