STM32理论 —— μCOS-Ⅲ(新)
文章目录
- 1. 任务调度器
- 1.1 抢占式调度
-
μCos-Ⅲ全称是Micro C OS Ⅲ,由Micriμm 公司发布的一个基于C 语言编写的第三代小型实时操作系统(RTOS);
-
RTOS 与裸机相比最大的优势在于多任务管理与实时性,它提供了多任务管理和任务间通信的功能;
-
μCOS-Ⅲ与FreeRTOS的区别:μCOS-III 的源码可读性比较强,代码写的非常规范。国内资料较多;
-
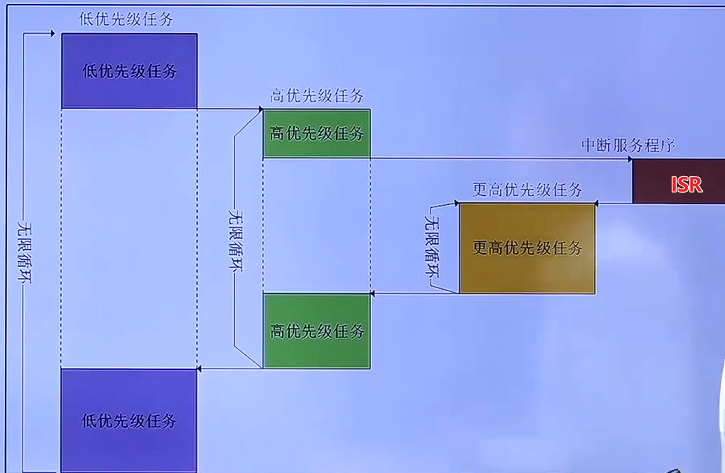
RTOS 的任务调度结构:如下图,高优先级任务能抢占低优先级任务,而中断能打断任意任务,每个任务都有自己的任务堆栈,用于保存任务的寄存器值;除非高优先级任务挂起,否则在一直运行高优先级任务过程中,低优先级任务无法被运行;
-
μCos-Ⅲ官方文档:https://micrium.atlassian.net/wiki/spaces、https://docs.silabs.com/micrium/latest/micrium-common-api/
1. 任务调度器
任务调度器就是决定当前执行哪个任务;
μCos-Ⅲ 支持2种任务调度方式:
- 抢占式调度:针对优先级不同的任务,优先级高的任务可抢占优先级低的任务;
- 时间片调度:针对优先级相同的任务,当多个任务优先级相同且就绪时,调度器会根据用户设置的时间片轮流运行这些任务。时间片以一次系统时钟节拍为单位(滴答定时器的中断频率),µC/OS-III 默认设置的任务时间片为 100,则 µC/OS-III 会在当前任务运行 100 次系统时钟节拍的时间后,切换到另一个相同任务优先级的任务中运行。
1.1 抢占式调度
- 创建3个任务;
- 任务1、任务2、任务3的优先级分别设置为3、2、1(数字越小,优先级越高);
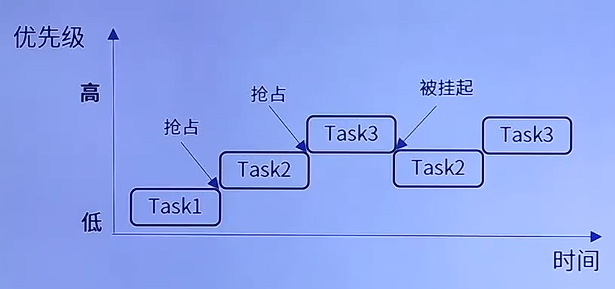
参考:
- 正点原子;
相关文章:

STM32理论 —— μCOS-Ⅲ(新)
文章目录 1. 任务调度器1.1 抢占式调度 μCos-Ⅲ全称是Micro C OS Ⅲ,由Micriμm 公司发布的一个基于C 语言编写的第三代小型实时操作系统(RTOS); RTOS 与裸机相比最大的优势在于多任务管理与实时性,它提供了多任务管理和任务间通信的功能&a…...

衢州知识付费系统报价,教师如何做精品课程?怎么创造精品课程?
精品课程对于学生的意义来说是不同的,越是精品让学习的人就越觉得值得,所以,做为教师来说,做出精品课程不仅仅是对学生负责,也是对自己负责,那如何做精品课程?相信很多教师们也想知道。 如何创造精品课程?…...

在Vue中,可以通过使用<slot>元素和name属性来创建具名插槽。这样您就可以为一个组件的不同部分定义不同的内容。 以下是一个简单的示例:
在Vue中,可以通过使用元素和name属性来创建具名插槽。这样您就可以为一个组件的不同部分定义不同的内容。 以下是一个简单的示例: <template><div><header><slot name"header"></slot></header><mai…...
C++笔试强训day19
目录 1.小易的升级之路 2.礼物的最大价值 3.对称之美 1.小易的升级之路 链接 模拟就行,唯一可能是难点得就是gcd(最大公约数) #include <iostream> using namespace std; #define int long long const int N 1e5 10; int arr[N];…...
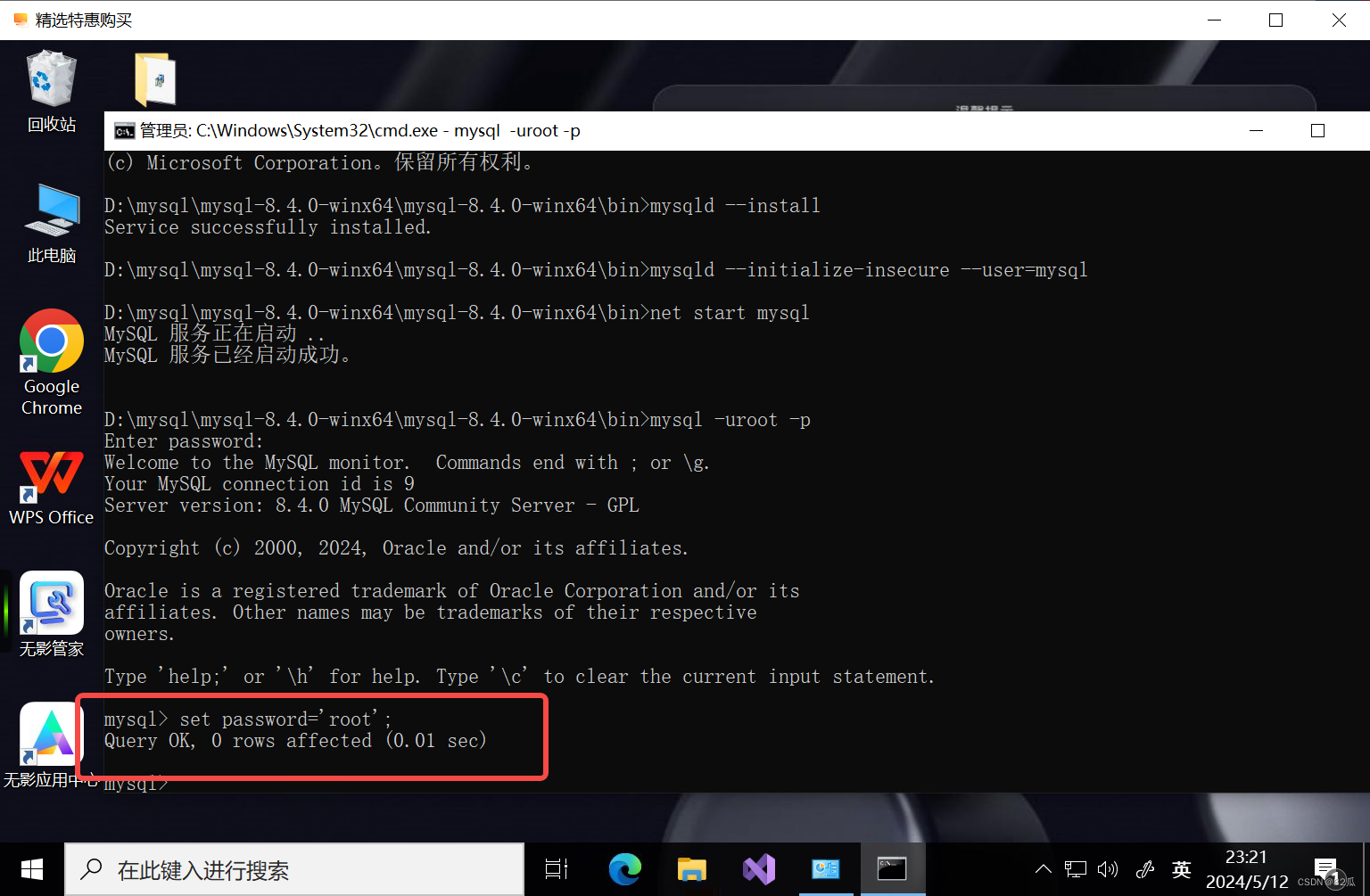
MySQL软件安装基于压缩包
打开mysql官网网址 MySQL :: Download MySQL Community Server 本次针对版本8的安装包方式进行安装,下载成功后接下来对MySQL进行安装 下载后有一个以zip后缀结尾的压缩包文件 对于安装包方式安装,比起可视化安装省去了许多安装步骤,这里直接…...

04 贝尔曼最优公式
贝尔曼最优公式 前言1、Motivating examples2、Definition of optimal policy3、Bellman optimality equation(BOE):Introduction4、 BOE:Maximization on the right-hand side5、BOE:Rewrite as v f(v)6、Contraction mapping theorem7、BO…...

印象笔记使用技巧
印象笔记(Evernote)是一款广泛使用的笔记应用,它帮助用户整理个人信息、文件和备忘录。以下是一些提高在印象笔记中效率的使用技巧: ### 1. 使用标签和笔记本组织笔记 - **建立笔记本**:为不同的项目或类别创建笔记本…...
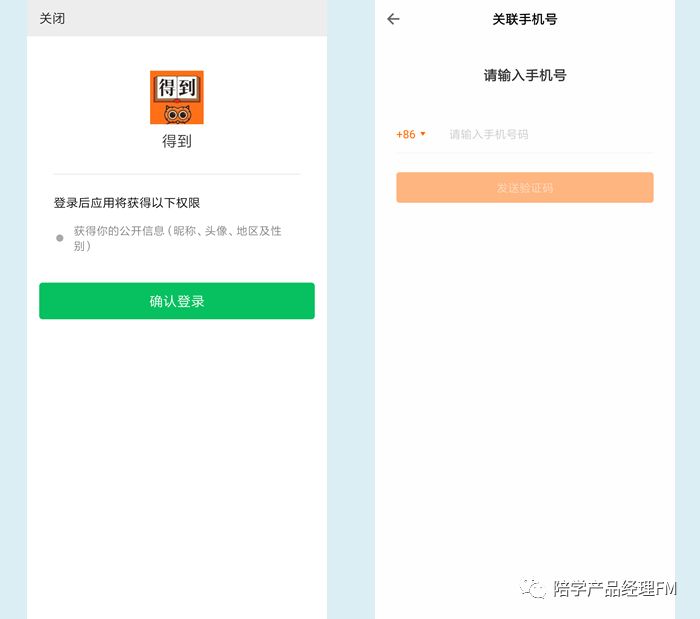
产品设计中的“注册”说明
在使用网站或应用的时候必不可少的就是账号系统,账号系统有些人可能觉得简单,无非就是账号密码。真的是这样吗? 一个完整的账号系统通常大家会分成四部分: 1.注册(手机号、邮箱、用户名/密码限制/验证码)…...
【linux学习】多线程(1)
文章目录 线程的概念线程与进程 线程的用法线程的创建多线程 线程的等待线程锁死锁 线程的概念 在Linux中,线程(Thread)是程序执行流的最小单位,是进程中的一个实体,负责在程序中执行代码。线程本身不拥有系统资源&…...

Leetcode 3149. Find the Minimum Cost Array Permutation
Leetcode 3149. Find the Minimum Cost Array Permutation 1. 解题思路2. 代码实现 题目链接:3149. Find the Minimum Cost Array Permutation 1. 解题思路 这一题的话就是一个动态规划的问题,不过他这个错位着实是把题目变得复杂了不少,唉…...

Python | 为列表中的元素分配唯一值
我们可以给列表中的所有数字分配一个唯一的值,重复时它会保留给它的值。这是一个非常常见的问题,在Web开发中,处理物品id时会遇到。让我们讨论一下解决这个问题的一些方法。 1. 使用enumerate() 列表解析 # initializing list test_list …...
HTML炫酷的相册
目录 写在前面 HTML简介 完整代码 代码分析 系列推荐 写在最后 写在前面 本期小编给大家带来一个炫酷的旋转相册,快来解锁属于你的独家记忆吧! HTML简介 HTML(全称为超文本标记语言)是一种用于创建网页结构和内容的标记语…...
C++笔试强训day20
目录 1.经此一役小红所向无敌 2.连续子数组最大和 3.非对称之美 1.经此一役小红所向无敌 链接 简单模拟即可。 需要注意的是: 除完之后有无余数,若有,则还可以再挨一次打。 #include <iostream> using namespace std; #define in…...

【PHP【实战项目】系统性教学】——使用最精简的代码完成用户的登录与退出
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
Linux下的常用基本指令
基本指令 前言一、ls 指令语法功能常用选项举例注意要点关于拼接关于 -a关于文件ls与/的联用ls与根目录ls与任意文件夹ls与常用选项与路径 ls -d与ls -ldls与ll 二、pwd命令语法功能常用选项注意要点window与Linux文件路径的区别家目录 三、cd 指令语法功能举例注意要点cd路径.…...

phpstorm环境配置与应用
在 PhpStorm 中配置 PHP 开发环境及进行一些常用的应用设置涉及以下几个主要步骤: ### 1. 安装和激活 PhpStorm - **下载安装**: 访问 JetBrains 官网下载最新版本的 PhpStorm 安装包,然后按照提示进行安装。 - **激活**: 启动 PhpStorm,你可…...

【Qt 学习笔记】Qt常用控件 | 布局管理器 | 水平布局Horizontal Layout
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt常用控件 | 布局管理器 | 水平布局Horizontal Layout 文章编号&…...
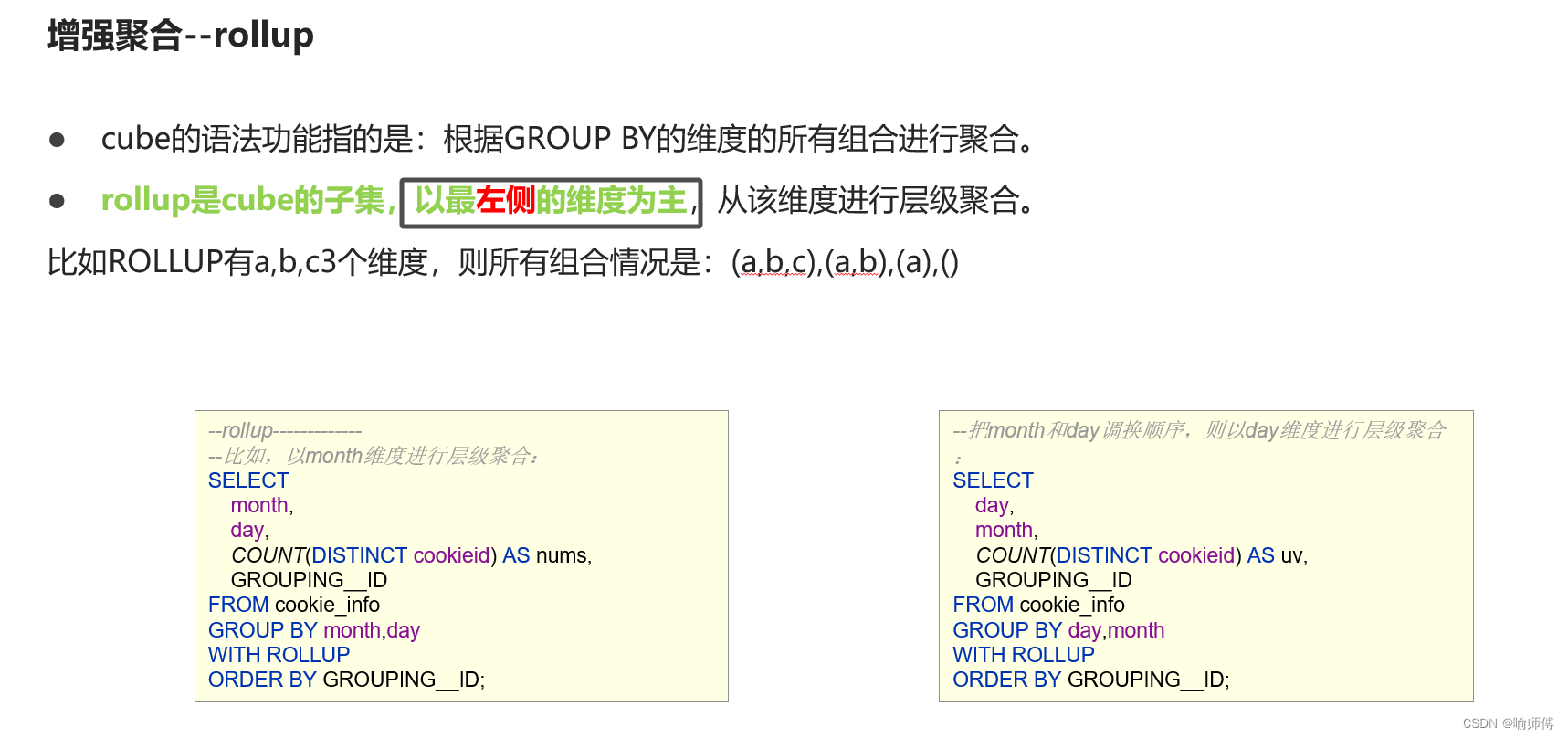
Hive Aggregation 聚合函数
Hive Aggregation 聚合函数 基础聚合 增强聚合...
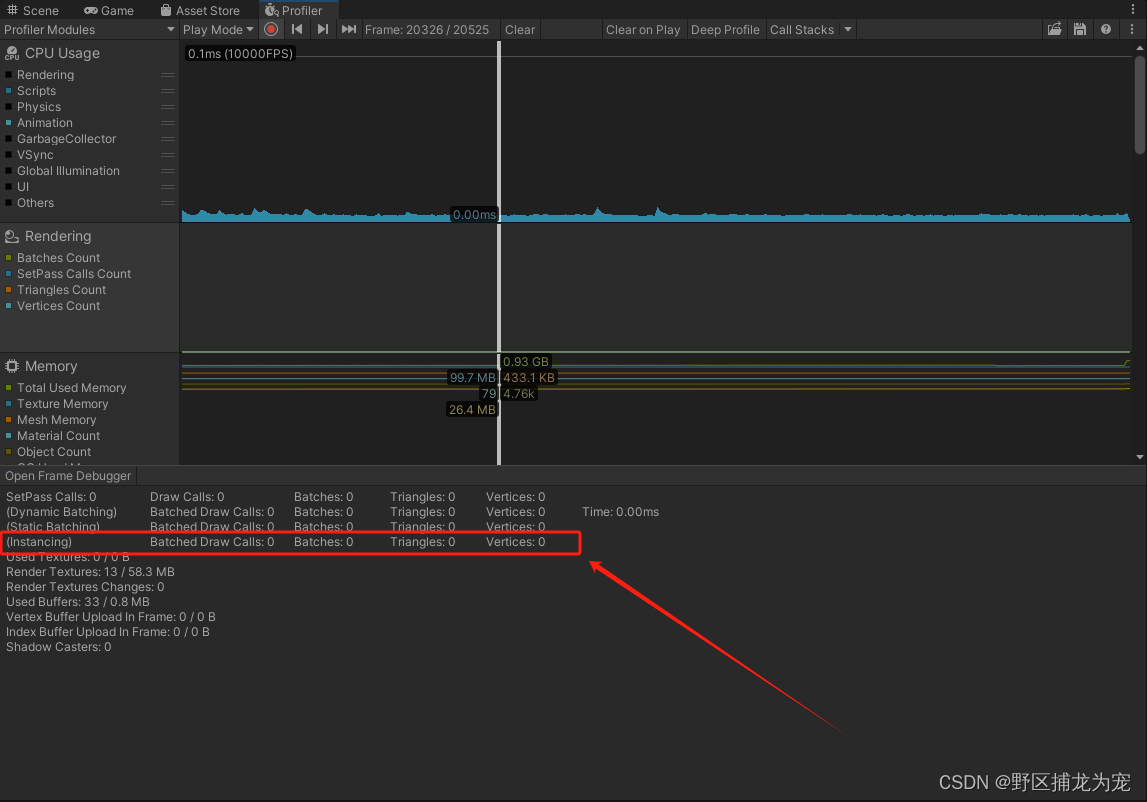
Unity 性能优化之GPU Instancing(五)
提示:仅供参考,有误之处,麻烦大佬指出,不胜感激! 文章目录 前言一、GPU Instancing使用方法二、使用GPU Instancing的条件三、GPU Instancing弊端四、注意五、检查是否成功总结 前言 GPU Instancing也是一种Draw call…...
LeetCode 138. 随机链表的复制
目录 1.原题链接: 2.结点拆分: 代码实现: 3.提交结果: 4.读书分享: 1.原题链接: 138. 随机链表的复制 2.结点拆分: ①.拷贝各个结点,连接在原结点后面; ②.处…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
