发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解
文章目录
- [发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解](https://cyj666.blog.csdn.net/article/details/138514145)
- 先来看一下最简单的`struct GemmIdentityThreadblockSwizzle`结构体
发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解
- 在CSDN著名文章发表博客之:cutlass demo讲解,在sm75机器上用cuda core计算fp32矩阵乘!深入理解cutlass::gemm::device::Gemm类 ,感兴趣的老乡别走开!!里面我们介绍了
cutlass::gemm::device::Gemm的使用方式,以及这个模版类的一些参数,里面有一个模版参数叫ThreadblockSwizzle,并且当时他还有一个默认值typename threadblock::GemmIdentityThreadblockSwizzle<>,,不知道各位看官是否还记得,现在我要告诉你这个模版参数的准确作用!开心吗?
- 首先这个文件的github地址是cutlass/gemm/threadblock/threadblock_swizzle.h
- 我们知道,cuda 处理问题都是将一个很大规模的问题分成很多个小问题,每个小问题由一个ThreadBlock来处理,而
ThreadblockSwizzle就是负责将逻辑上的小问题映射到cuda上的ThreadBlock上。 - 或者直接引用这个文件上的注释吧!
Implements several possible threadblock-swizzling functions mapping blockIdx to GEMM problems.
先来看一下最简单的struct GemmIdentityThreadblockSwizzle结构体
- 这个结构体有一个默认参数是1。
template <int N = 1>
struct GemmIdentityThreadblockSwizzle {CUTLASS_HOST_DEVICEGemmIdentityThreadblockSwizzle() { }/// Returns the shape of the problem in units of logical tiles/// *Gemm* problem size: gemm(M, N, K)/// 这个函数的作用是简单的。/// 就是以tile_size为逻辑单元,整个问题的逻辑shape!CUTLASS_HOST_DEVICEstatic GemmCoord get_tiled_shape(GemmCoord problem_size,GemmCoord tile_size,int split_k_slices) {return GemmCoord((problem_size.m() + tile_size.m() - 1) / tile_size.m(),(problem_size.n() + tile_size.n() - 1) / tile_size.n(),split_k_slices);}/// Returns the shape of the problem in units of logical tiles/// *ImplicitGemm* Conv2d problem size: conv_operator(NPQK, NHWC, KRSC)CUTLASS_HOST_DEVICEstatic GemmCoord get_tiled_shape(cutlass::conv::Operator conv_operator,cutlass::conv::Conv2dProblemSize const &problem_size,GemmCoord tile_size,int split_k_slices) {gemm::GemmCoord implicit_gemm_problem_size = cutlass::conv::implicit_gemm_problem_size(conv_operator, problem_size);return get_tiled_shape(implicit_gemm_problem_size, tile_size, split_k_slices);}/// Returns the shape of the problem in units of logical tiles/// *ImplicitGemm* Conv3d problem size: conv_operator(NZPQK, NDHWC, KTRSC)CUTLASS_HOST_DEVICEstatic GemmCoord get_tiled_shape(cutlass::conv::Operator conv_operator,cutlass::conv::Conv3dProblemSize const &problem_size,GemmCoord tile_size,int split_k_slices) {gemm::GemmCoord implicit_gemm_problem_size = cutlass::conv::implicit_gemm_problem_size(conv_operator, problem_size);return get_tiled_shape(implicit_gemm_problem_size, tile_size, split_k_slices);}/// 这个函数是获得物理shape!也就是三对三对<<<>>>下的grid_shape!/// Computes CUDA grid dimensions given a size in units of logical tilesCUTLASS_HOST_DEVICEstatic dim3 get_grid_shape(GemmCoord tiled_shape) {int tile = 1 << get_log_tile(tiled_shape);return dim3(tiled_shape.m() * tile, (tiled_shape.n() + tile - 1) / tile, tiled_shape.k());}
- 下面的这个函数来获得最好的
get_log_tile!
/// 这个是防止函数是防止逻辑shape上的n过大,导致grid的第2维过大!/// Calculates optimal swizzle widthCUTLASS_HOST_DEVICEstatic int get_log_tile(GemmCoord tiled_shape) {auto n = tiled_shape.n();// Thresholds picked so that it doesn't cause too many no-op CTAsif (N >= 8 && n >= 6)return 3;else if (N >= 4 && n >= 3)return 2;else if (N >= 2 && n >= 2)return 1;elsereturn 0;}
- 下面两个函数是同一个名字,get_tile_offset,但是参数不同。
- 他们的共同作用根据物理id是获取
逻辑上Tile的偏移量!
- 他们的共同作用根据物理id是获取
- 但是第二个函数好像很少用到的样子!
/// Obtains the threadblock offset (in units of threadblock-scoped tiles)CUTLASS_DEVICEstatic GemmCoord get_tile_offset(int log_tile) {int block_idx_x = RematerializeBlockIdxX();int block_idx_y = RematerializeBlockIdxY();int block_idx_z = RematerializeBlockIdxZ();return GemmCoord{(block_idx_x >> log_tile), //(block_idx_y << log_tile) + ((block_idx_x) & ((1 << (log_tile)) - 1)),block_idx_z};}/// Obtains the threadblock offset (in units of threadblock-scoped tiles)CUTLASS_DEVICEstatic GemmCoord get_tile_offset(GemmCoord tiled_shape) {int const kTile = N;int block_idx_x = RematerializeBlockIdxX();int block_idx_y = RematerializeBlockIdxY();if ((tiled_shape.m() < kTile) || (tiled_shape.n() < kTile))return GemmCoord{block_idx_x, block_idx_y, RematerializeBlockIdxZ()};return GemmCoord{(block_idx_x / kTile),(block_idx_y * kTile) + (block_idx_x % kTile),RematerializeBlockIdxZ()};}
};
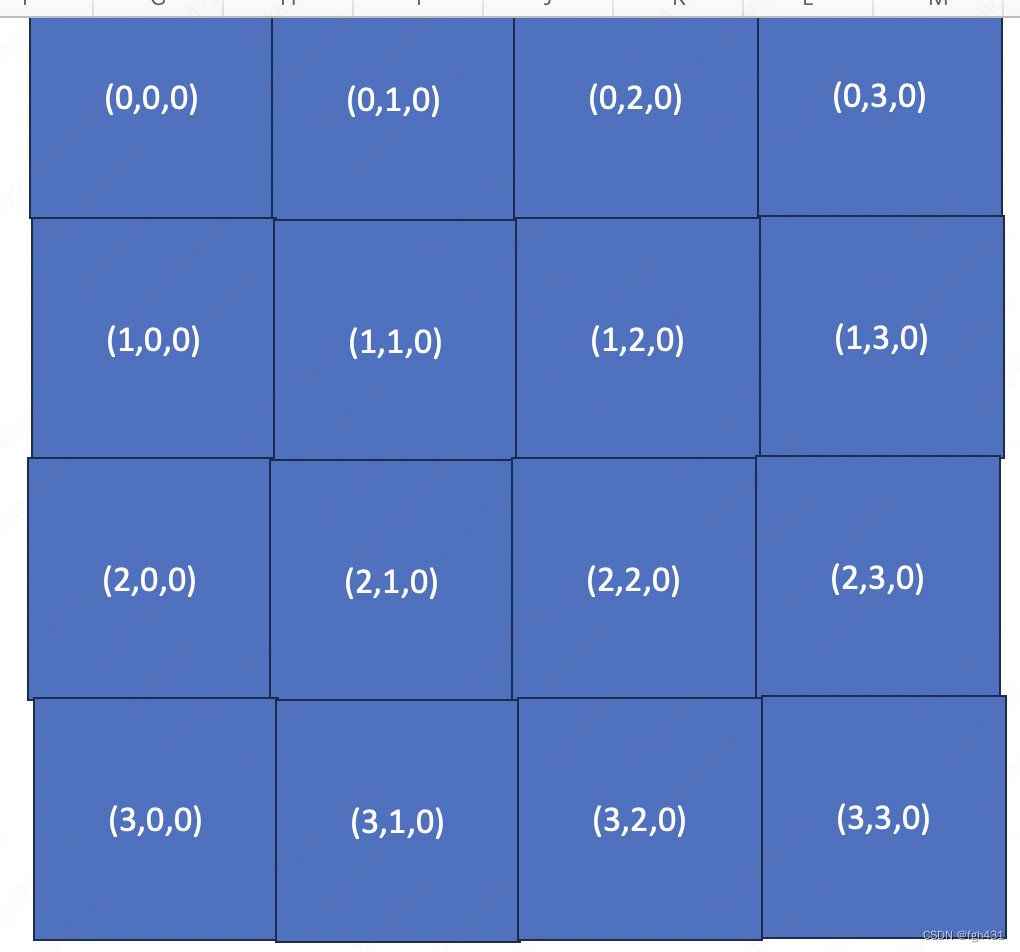
- 举个例子,假设N=1,并且 C C C输出矩阵被分成下面这样的逻辑shape,
- 那么三对<<<>>>发射的grid就是(4,4,1)!
- 那么每个Tile被映射到的ThreadBlock id如下图所示。
-
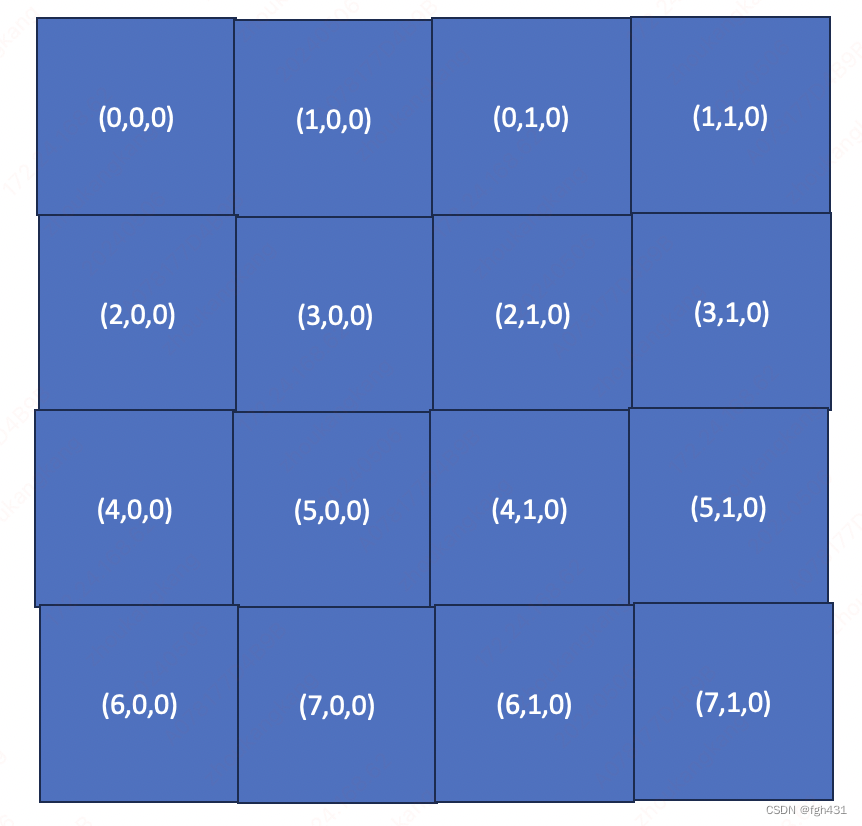
如果 N = 2 N=2 N=2,
-
那么三对<<<>>>发射的grid就是(8,2,1)!
-
那么每个Tile被映射到的ThreadBlock id如下图所示。
相关文章:

发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解
文章目录 [发表博客之:gemm/threadblock/threadblock_swizzle.h 文件夹讲解,cutlass深入讲解](https://cyj666.blog.csdn.net/article/details/138514145)先来看一下最简单的struct GemmIdentityThreadblockSwizzle结构体 发表博客之:gemm/th…...

【C语言项目】贪吃蛇(下)
个人主页~ 源码在Gitee仓库~ 上一篇贪吃蛇(上)~ 贪吃蛇 四、核心的实现游戏测试1、GameStart(1)控制台窗口大小和名字设置(2)光标隐藏(3)打印欢迎界面(4)创建…...

【Unity实战|热更】Addressable读取SO文件报错解决
情景再现 假定你有一个Unity工程,使用了HybridCLR和Addressable,SO文件存放在Addressable中。热更加载后进入游戏场景出现了SO文件读取报错: UnityEngine.AddressableAssets.InvalidKeyException: Exception of type UnityEngine.Addressab…...
Web自动化 - selenium
文章目录 一、selenium的使用selenium的安装 二、元素1. 定位选择元素1.id 定位2. class_name 定位find_element 和 find_elements的区别3. TAG_NAME 定位4. 超链接 定位 2. 操控元素1. 查询内容2. 获取元素文本内容3. 获取元素属性 3. 浏览器常用操作API4. 鼠标操作 - perform…...

基于select for update 实现数据库分布式锁
1、select for update 的基本语法 SELECT * FROM table_name WHERE condition FOR UPDATE;2、select for update 的定义及作用 2.1 、select for update的含义是在查询数据的同时对所选的数据行进行锁定,以保证数据的一致性和并发控制。在并发环境下,多…...
Java后端实现对象与文件接收数据(minio测试)
实现思路: 1. 两个接口实现,一个接对象数据(file),一个接文件数据(json)。 2. json对象(base64String) 实体类信息 ,请求体统一接收 3. file, String name ,String password ,String name , Controller层接收 统一…...

考研踩坑经验分享
文章目录 写在前面自身情况简介自身学习路线优点坑点 学习路线建议1、2和3月份3、4和5月份6、7和8月份9、10月份11、12月份 一些私货建议结尾 写在前面 考研是一件非常有盼头的事,但绝对不是一件容易的事。 如果你不能做好来年三月份出成绩时,坦然接受…...
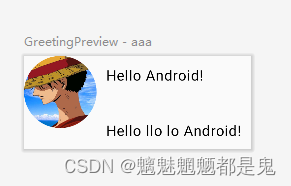
Android Compose 一:基础控件
Flutter 与 Compose 组件辣么像,难道是同一个google团队整的;也未深究,只是猜测。 创建项目 需要使用新版本Android studio,忽略步骤… 项目目录 MainActivity说明 1 系统默认页面 Preview 修饰的方法,只用来供开发…...
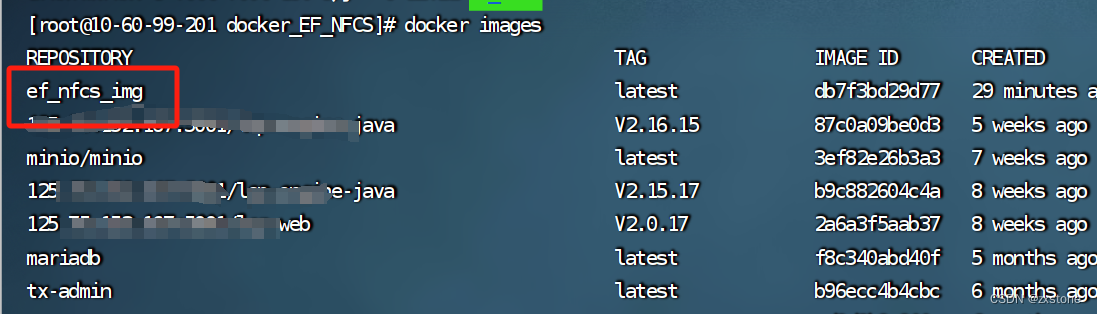
python3.12.0 在Linux 制作镜像包 部署到docker 全过程
项目结构: 比如,在pycharm里需要运行 themain.py 1、上传Linux的目录结构: Dockerfile 文件需要制作: 这里是关键: #基于的基础镜像 FROM python:3.12.0 #代码添加到code文件夹 ADD ./EF_NFCS /code #设置code文…...
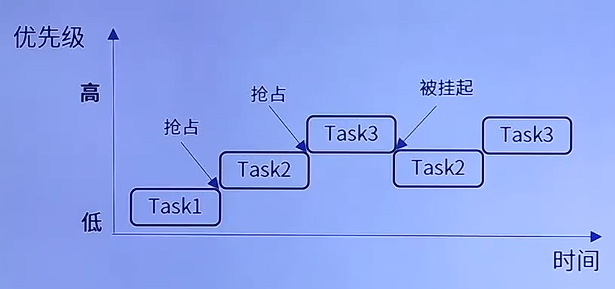
STM32理论 —— μCOS-Ⅲ(新)
文章目录 1. 任务调度器1.1 抢占式调度 μCos-Ⅲ全称是Micro C OS Ⅲ,由Micriμm 公司发布的一个基于C 语言编写的第三代小型实时操作系统(RTOS); RTOS 与裸机相比最大的优势在于多任务管理与实时性,它提供了多任务管理和任务间通信的功能&a…...

衢州知识付费系统报价,教师如何做精品课程?怎么创造精品课程?
精品课程对于学生的意义来说是不同的,越是精品让学习的人就越觉得值得,所以,做为教师来说,做出精品课程不仅仅是对学生负责,也是对自己负责,那如何做精品课程?相信很多教师们也想知道。 如何创造精品课程?…...

在Vue中,可以通过使用<slot>元素和name属性来创建具名插槽。这样您就可以为一个组件的不同部分定义不同的内容。 以下是一个简单的示例:
在Vue中,可以通过使用元素和name属性来创建具名插槽。这样您就可以为一个组件的不同部分定义不同的内容。 以下是一个简单的示例: <template><div><header><slot name"header"></slot></header><mai…...
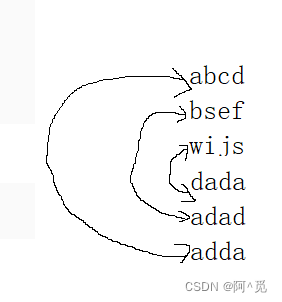
C++笔试强训day19
目录 1.小易的升级之路 2.礼物的最大价值 3.对称之美 1.小易的升级之路 链接 模拟就行,唯一可能是难点得就是gcd(最大公约数) #include <iostream> using namespace std; #define int long long const int N 1e5 10; int arr[N];…...
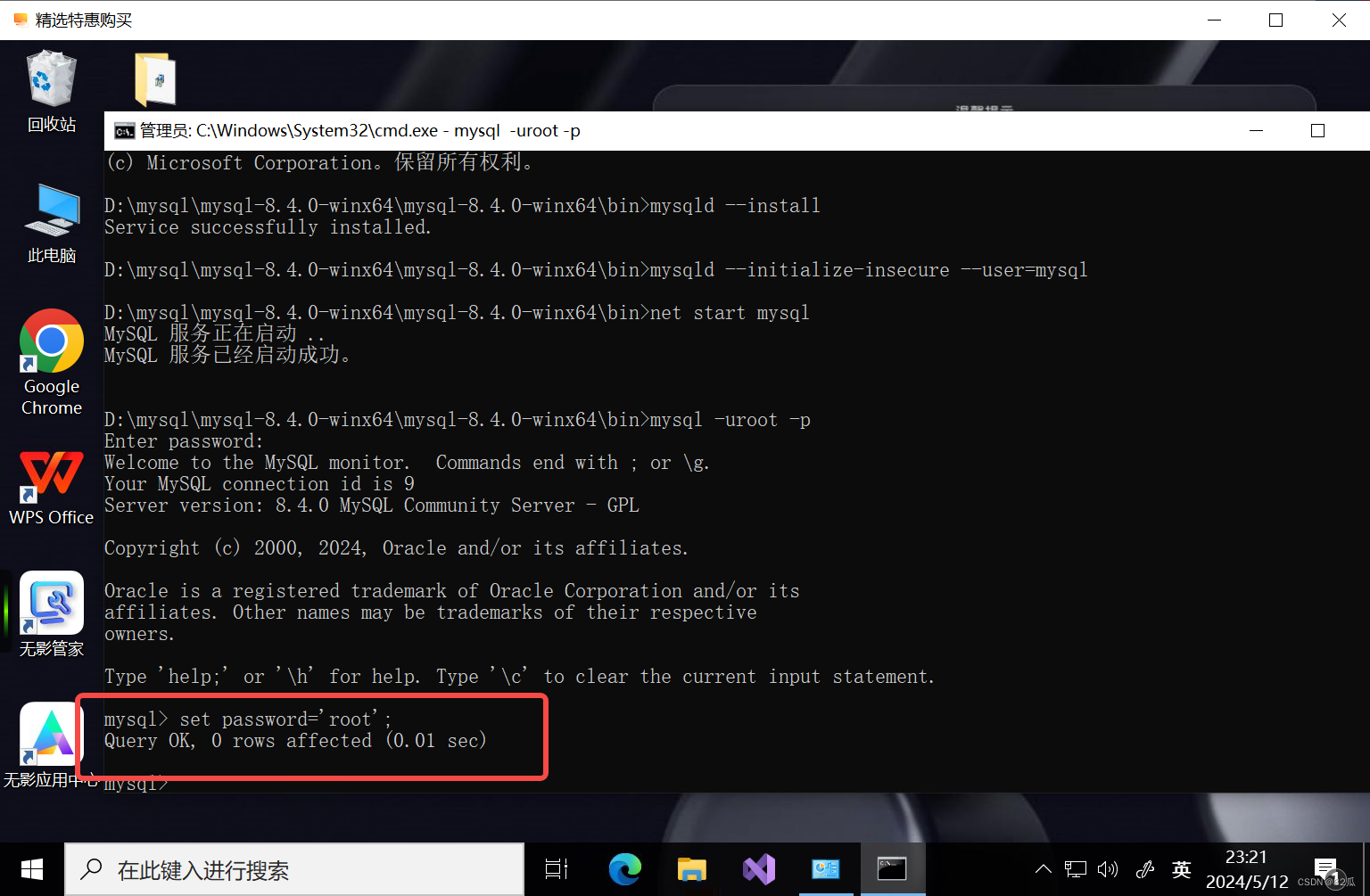
MySQL软件安装基于压缩包
打开mysql官网网址 MySQL :: Download MySQL Community Server 本次针对版本8的安装包方式进行安装,下载成功后接下来对MySQL进行安装 下载后有一个以zip后缀结尾的压缩包文件 对于安装包方式安装,比起可视化安装省去了许多安装步骤,这里直接…...

04 贝尔曼最优公式
贝尔曼最优公式 前言1、Motivating examples2、Definition of optimal policy3、Bellman optimality equation(BOE):Introduction4、 BOE:Maximization on the right-hand side5、BOE:Rewrite as v f(v)6、Contraction mapping theorem7、BO…...

印象笔记使用技巧
印象笔记(Evernote)是一款广泛使用的笔记应用,它帮助用户整理个人信息、文件和备忘录。以下是一些提高在印象笔记中效率的使用技巧: ### 1. 使用标签和笔记本组织笔记 - **建立笔记本**:为不同的项目或类别创建笔记本…...
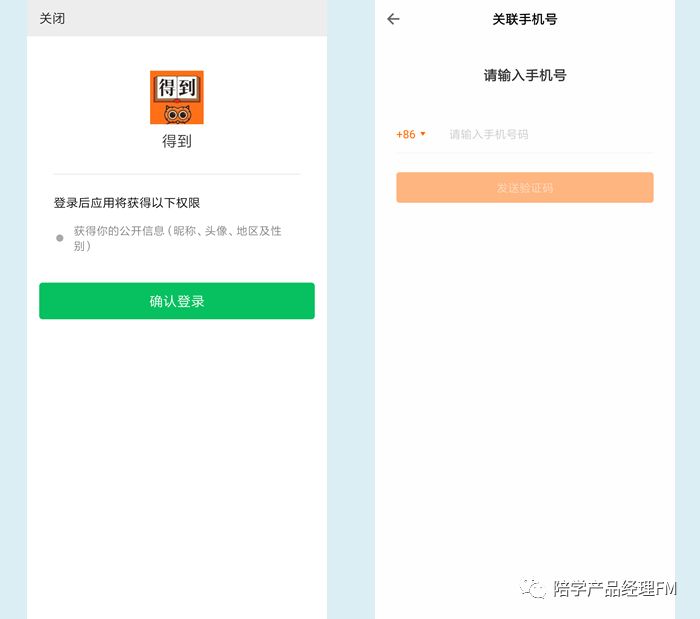
产品设计中的“注册”说明
在使用网站或应用的时候必不可少的就是账号系统,账号系统有些人可能觉得简单,无非就是账号密码。真的是这样吗? 一个完整的账号系统通常大家会分成四部分: 1.注册(手机号、邮箱、用户名/密码限制/验证码)…...
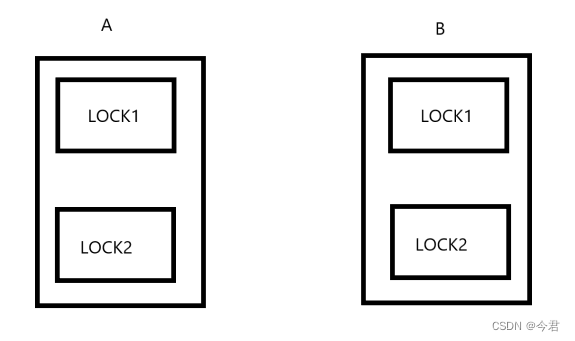
【linux学习】多线程(1)
文章目录 线程的概念线程与进程 线程的用法线程的创建多线程 线程的等待线程锁死锁 线程的概念 在Linux中,线程(Thread)是程序执行流的最小单位,是进程中的一个实体,负责在程序中执行代码。线程本身不拥有系统资源&…...

Leetcode 3149. Find the Minimum Cost Array Permutation
Leetcode 3149. Find the Minimum Cost Array Permutation 1. 解题思路2. 代码实现 题目链接:3149. Find the Minimum Cost Array Permutation 1. 解题思路 这一题的话就是一个动态规划的问题,不过他这个错位着实是把题目变得复杂了不少,唉…...

Python | 为列表中的元素分配唯一值
我们可以给列表中的所有数字分配一个唯一的值,重复时它会保留给它的值。这是一个非常常见的问题,在Web开发中,处理物品id时会遇到。让我们讨论一下解决这个问题的一些方法。 1. 使用enumerate() 列表解析 # initializing list test_list …...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
