最短路径[floyd算法]-----视频讲解+代码实现
求最短路径,一般有三种方法:
单源最短路径--Dijkstra算法
此算法只能求不带负权值的有向无环图
单源最短路径--Bellman-Ford算法(少考)
此算法优点在于:可以求带权值的右向无环图
但只是缺点明显,时间复杂度很高,相当于暴力求解。
多源最短路径--Floyd-Warshall算法
此算法可以解决任意两点间的最短路径,也可以求带负权值的右向无环图。
单源的意思是只能从指定位置开始,求其他位置的最短路径。
多源则不同,可以求任意两点间的最短路径。
本文章主要讲解floyd算法。
floyd算法逻辑:
想要理解floyd算法的实现逻辑,最形象的视频讲解是很有必要的。
这里小编极力推荐B站蓝不过海呀这个Up的视频讲解,讲的非常细节,
比自己去看一些什么算法导论效率要高的多,毕竟相较于文字,
人对图形化的东西更有印象。
B站连接:图-最短路径-Floyd(弗洛伊德)算法
视频中只是对算法的逻辑进行了讲解,但是没有涉及代码的实现,接下来,
我会依照视频讲解逻辑,补充一个JAVA代码的实现方式,文章末尾附带源码。
代码实现:
因为此算法,操作对象是一个图,所以我们先来介绍一下图在JAVA代码中的储存方式:
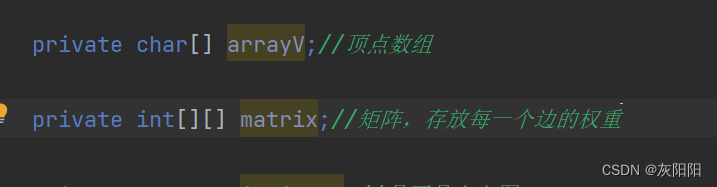
好了,开始切入正题。
在视频中,运用到了两个矩阵,一个是用来存路径长度的,一个使用来存路径的。
所以我们在定义函数参数时,也要定义两个二维数组:

在视频中,Up主先对这两个矩阵进行了初始化:
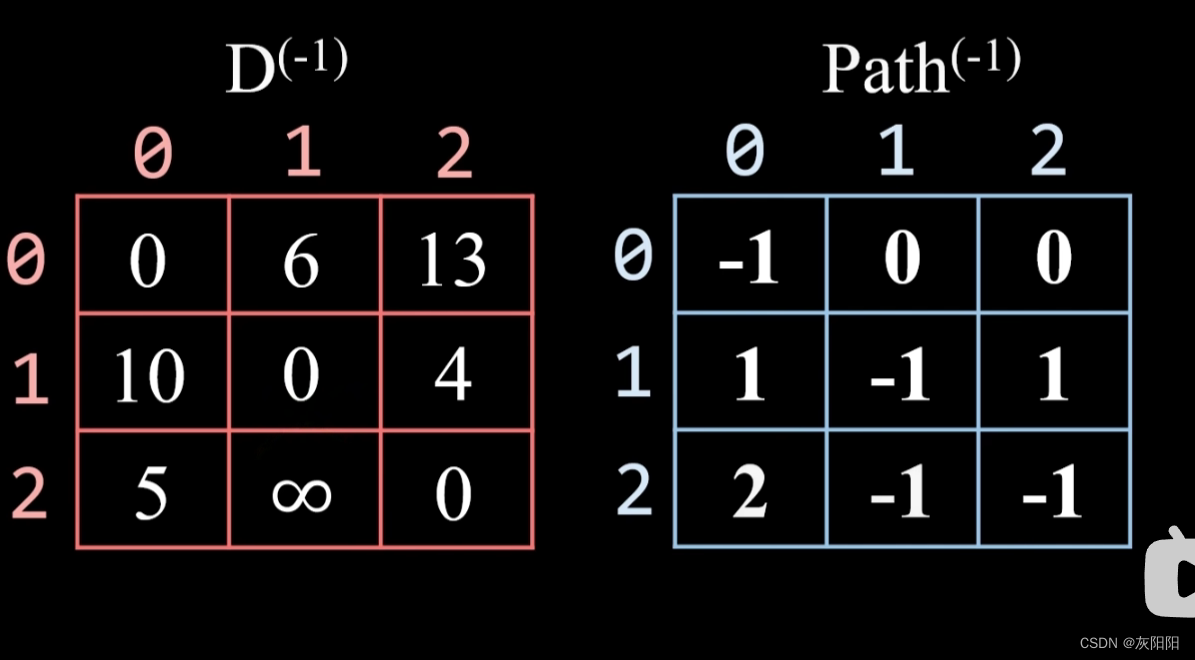
D矩阵是放路径长度的(也就是权值)-->这些信息从已经构造好的图里面获取:

而在代码中,就是从这个矩阵获取:

而Path矩阵的初始化,只需要按照D矩阵进行初始化即可。
接下来我们在代码中,去初始化这两个数组:
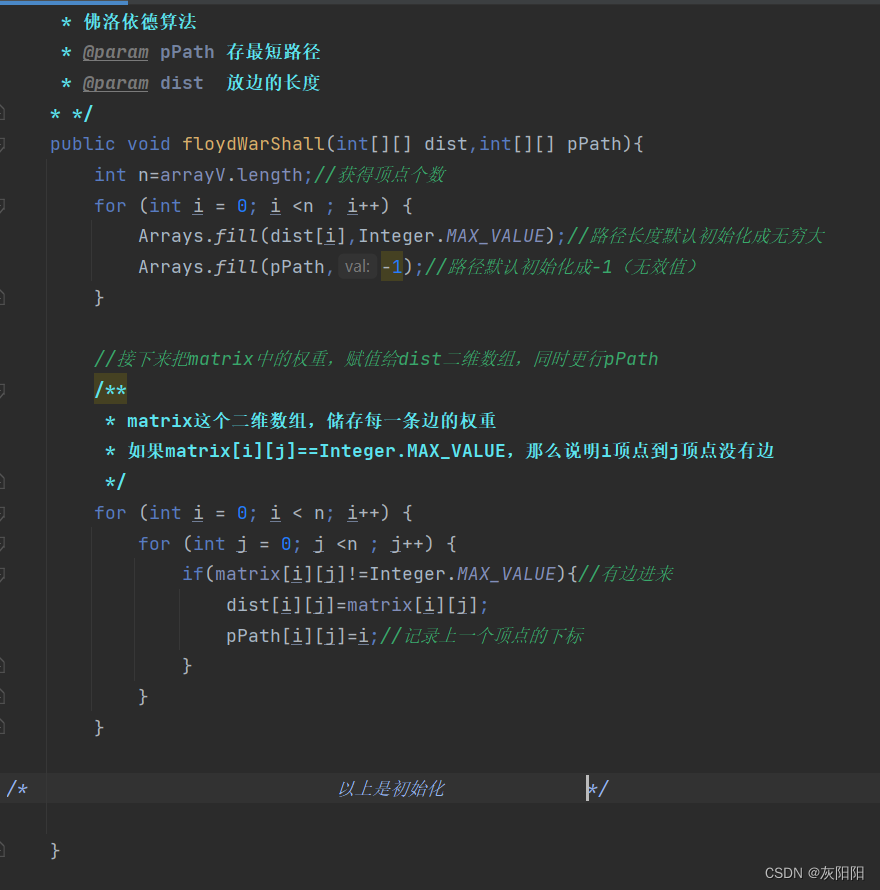
接下来,需要创建n个中间结点,从0开始,n是顶点的数量,所以定义一个循环:

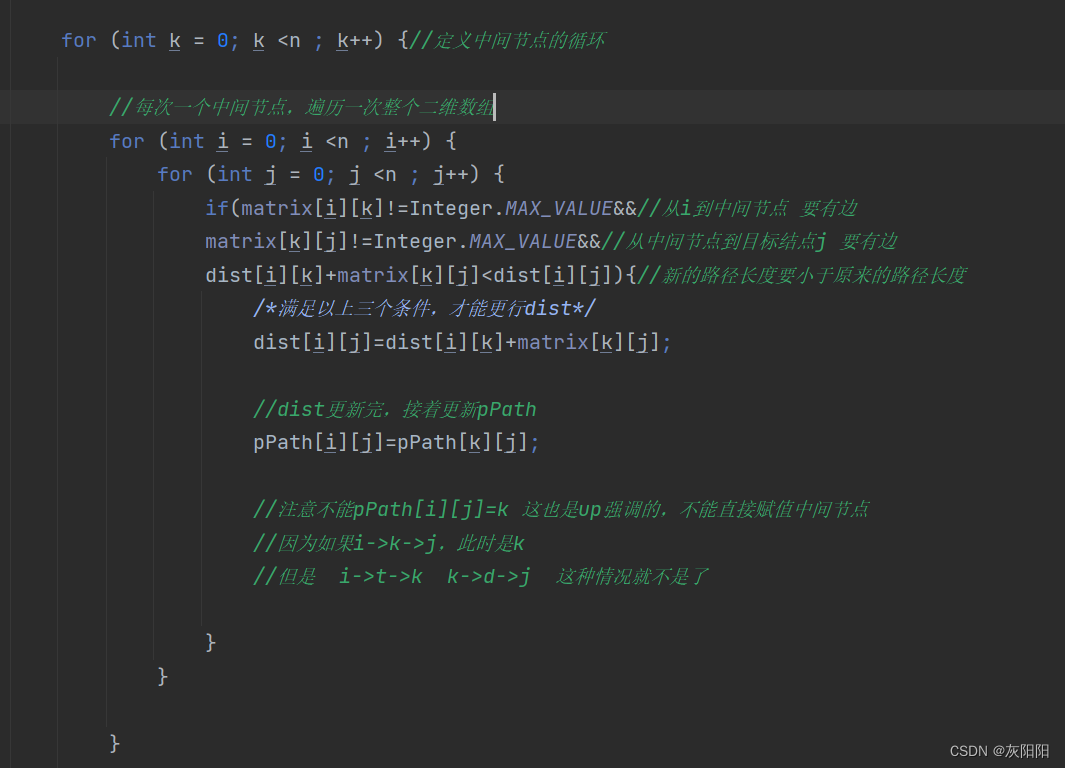
在这个循环体中,我们要一直执行一下操作:
通过旧的D矩阵,也就是代码中的dist二维数组,创建一个新的矩阵D。
然后依据新的矩阵D,也就是新的dist二维数组,
以及旧的Path矩阵(也就代码中的pPath二维数组)
创建一个新的矩阵Path(也就是新的pPath二维数组)。
循环已结束,那么dist二维数组,存的就是一个顶点到另一个顶点的的总长度了。
pPaht二维数组,就存着具体的路径了。
代码实现:
注意:
已知Path矩阵,求多源最短路径:
每一行的储存思路,和并查集寻找根结点的方式是一样的,最终逆置顶点顺序即可。
算法源码:
/*** 佛洛依德算法* @param pPath 存最短路径* @param dist 放边的长度* */public void floydWarShall(int[][] dist,int[][] pPath){int n=arrayV.length;//获得顶点个数for (int i = 0; i <n ; i++) {Arrays.fill(dist[i],Integer.MAX_VALUE);//路径长度默认初始化成无穷大Arrays.fill(pPath,-1);//路径默认初始化成-1(无效值)}//接下来把matrix中的权重,赋值给dist二维数组,同时更行pPath/*** matrix这个二维数组,储存每一条边的权重* 如果matrix[i][j]==Integer.MAX_VALUE,那么说明i顶点到j顶点没有边*/for (int i = 0; i < n; i++) {for (int j = 0; j <n ; j++) {if(matrix[i][j]!=Integer.MAX_VALUE){//有边进来dist[i][j]=matrix[i][j];pPath[i][j]=i;//记录上一个顶点的下标}}}/* 以上是初始化 */for (int k = 0; k <n ; k++) {//定义中间节点的循环//每次一个中间节点,遍历一次整个二维数组for (int i = 0; i <n ; i++) {for (int j = 0; j <n ; j++) {if(matrix[i][k]!=Integer.MAX_VALUE&&//从i到中间节点 要有边matrix[k][j]!=Integer.MAX_VALUE&&//从中间节点到目标结点j 要有边dist[i][k]+matrix[k][j]<dist[i][j]){//新的路径长度要小于原来的路径长度/*满足以上三个条件,才能更行dist*/dist[i][j]=dist[i][k]+matrix[k][j];//dist更新完,接着更新pPathpPath[i][j]=pPath[k][j];//注意不能pPath[i][j]=k 这也是up强调的,不能直接赋值中间节点//因为如果i->k->j,此时是k//但是 i->t->k k->d->j 这种情况就不是了}}}}}
相关文章:

最短路径[floyd算法]-----视频讲解+代码实现
求最短路径,一般有三种方法: 单源最短路径--Dijkstra算法 此算法只能求不带负权值的有向无环图 单源最短路径--Bellman-Ford算法(少考) 此算法优点在于:可以求带权值的右向无环图 但只是缺点明显,时间复杂度…...

图像/视频恢复和增强CodeFormer
github:https://github.com/sczhou/CodeFormer 尝试增强旧照片/修复人工智能艺术 面部修复 面部色彩增强和恢复 脸部修复...

WPF中ObservableCollection
在WPF(Windows Presentation Foundation)中,ObservableCollection<T> 是一个非常重要的类,它用于实现动态数据绑定功能。这个类位于 System.Collections.ObjectModel 命名空间中,是 ICollection<T>, IList…...

如何用鼠标点击在picturebox的图像上做标记
鼠标点击图像,在点击处画一个圆。 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Drawing.Drawing2D; using System.Linq; using System.Text; using System.Threading.T…...
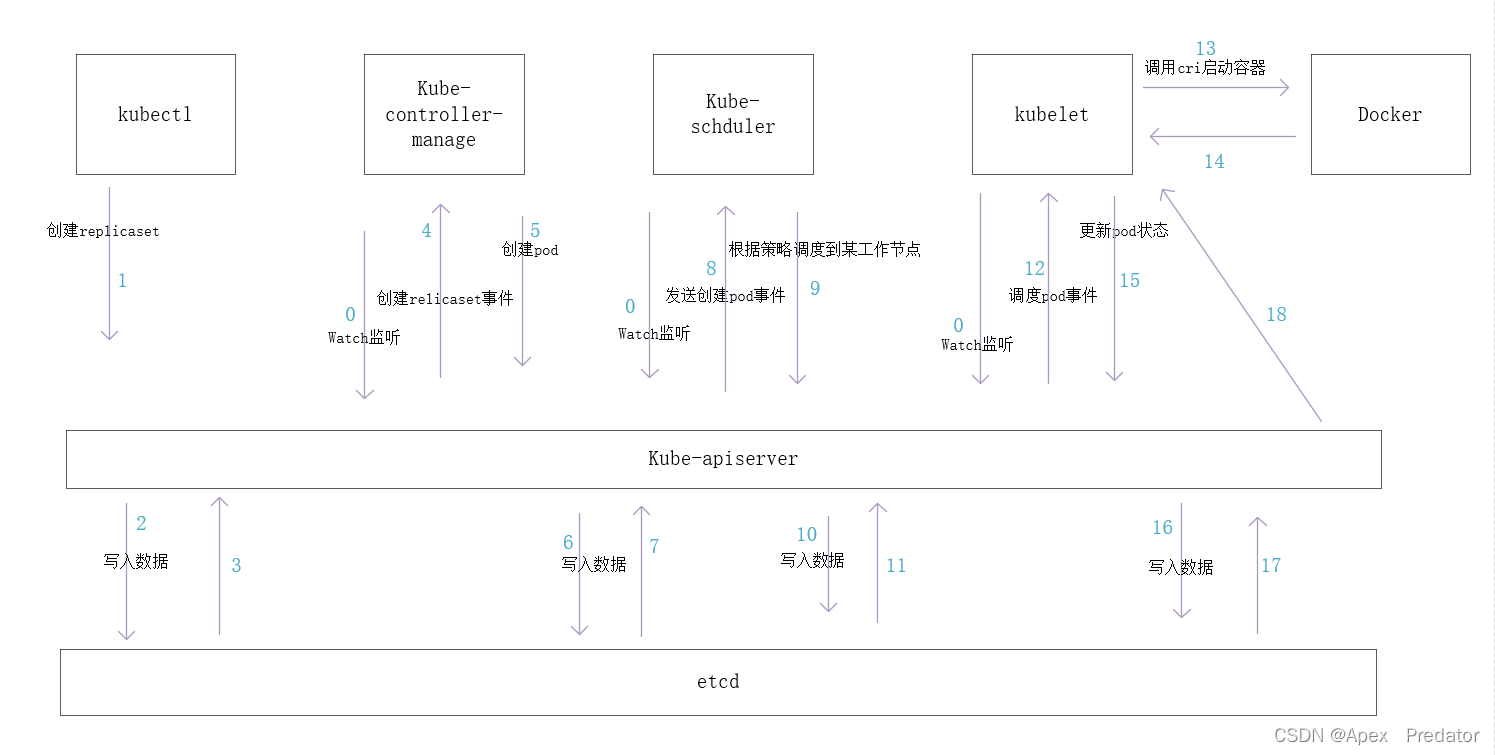
k8s介绍
一、前言 Kubernetes(通常简称为 K8s)是一个开源的容器编排平台,用于自动化部署、扩展和管理容器化应用程序,它提供了丰富的功能使得用户能够轻松地管理大规模的容器集群,包括自动化部署和扩展、服务发现和负载均衡、存…...

K-means聚类模型:深入解析与应用指南
K-means聚类是一种广泛使用的无监督学习算法,它通过迭代过程将数据集划分为K个聚类。以下是一篇关于K-means聚类模型的技术文章,将从不同的角度进行详尽的描述。 1. 引言 K-means聚类算法是一种简单且高效的聚类方法,广泛应用于数据挖掘、市…...

CTF-密码学基础
概述 密码学(Cryptolopy):是研究信息系统安全保密的科学 密码学研究的两个方向: 密码编码学(Cryptography):主要研究对信息进行编码,实现对信息的隐蔽密码分析学(Cryptanalytics):主要研究加密信息的破译或消息的伪造…...

代码随想录算法训练营day22 | 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
654.最大二叉树 和构造二叉树差不多,本题使用索引的方式 class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:return self.traversal(nums, 0, len(nums)-1)def traversal(self, nums, left, right):if left > r…...

企业信息防泄漏软件分析:盘点常用企业信息防泄漏软件
在当今数字化时代,企业信息防泄漏软件已成为保障企业数据安全不可或缺的一环。市面上众多的防泄漏软件各具特色,如何从中挑选出最适合自己企业的产品,成为了一个值得深入探讨的话题。 一、企业信息防泄漏软件分析 首先,我们需要…...

Rancher-Kubewarden-保姆级教学-含Demo测试
一、什么是Kubewarden? What is Kubewarden? | Kubewarden 1、就是容器集群的准入策略引擎。 1、使用的策略其实就是k8s原生的security context. 2、使用WebAssembly来编写策略。 1、WebAssembly,可以使用擅长的开发语言来编写策略。(下面的…...

Lumerical Script ------ array 数组类型 和 matrix 矩阵类型
Lumerical Script ------ array 数组类型 和 matrix 矩阵类型 引言正文array 数组类型matrix 矩阵类型引言 这篇仅仅用作个人笔记,因为作者本人比较擅长 Python,每次写 Lumerical Script 总是会写错代码。 正文 array 数组类型 Lumerical Script 脚本有些像 Matlab 脚本,…...
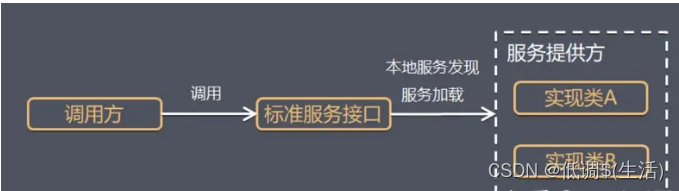
Springboot自动装配源码分析
版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.3.4.RELEASE</version><relativePath/> <!-- lookup parent from repository --> </par…...
模型详解 动图讲解)
Visual Transformer (ViT)模型详解 动图讲解
1 Vit简介 1.1 Vit的由来 ViT是2020年Google团队提出的将Transformer应用在图像分类的模型,虽然不是第一篇将transformer应用在视觉任务的论文,但是因为其模型“简单”且效果好,可扩展性强(scalable,模型越大效果越好),成为了transformer在CV领域应用的里程碑著作,也…...
(std::forward))
C++:完美转发(一)(std::forward)
一、理解引用折叠 (一)引用折叠 1. 在C中,“引用的引用”是非法的。像 auto& &rx x;(注意两个&之间有空格)这种直接定义引用的引用是不合法的,但是编译器在通过类型别名或模板参数推导等语境…...

西部首个全域直播基地,打造西部直播基地领军形象
天府锋巢直播产业基地作为西部直播产业的领军者,以其前瞻性的战略布局和卓越的服务体系,正加速推动全域直播的快速发展,助力直播产业实现新升级。该基地作为成都规模最大的直播基地,以加快全域直播为核心目标,通过促进…...

钟表——蓝桥杯十三届2022国赛大学B组真题
问题分析 这个问题的关键有两点:1.怎么计算时针,分针,秒针之间的夹角,2.时针,分针,秒针都是匀速运动的,并非跳跃性的。问题1很好解决看下面的代码就能明白,我们先考虑问题2…...

CSS 之 圆形波浪进度条效果
一、简介 本篇博客讲述了如何实现一个圆形波浪进度条的样式效果,具体效果参考下方GIF图。该样式的加载进度条可以用在页面跳转或数据处理等情况下的加载动画,比起普通的横条进度条来说,样式效果更生动美观。 实现思路: 这…...
)
按下鼠标进行拖拽,让元素跟随鼠标进行移动,鼠标抬起,元素停止移;js鼠标拖拽 (鼠标按下事件:onmousedown、鼠标移动事件:onmousemove、鼠标抬起事件:onmouseup)
需求如下: 按下鼠标进行拖拽,让元素跟随鼠标进行移动,鼠标抬起,元素停止移动。 解析: 鼠标按下事件:onmousedown 鼠标移动事件:onmousemove 鼠标抬起事件:onmouseup <!DOCT…...

第十二章 项目采购管理
12.1 规划采购管理 12.2 实施采购 12.3 控制采购 项目经理通常没有签订合同的权限,但必须熟悉正规的采购流程; 协议是采购的核心文件,关于协议我们要知道: 协议包括:合同、服务水平协议、谅解、协议备忘录或采购订单 ❗…...

PSFR-GAN复现
写在前面:本博客仅作记录学习之用,部分图片来自网络,如需引用请注明出处,同时如有侵犯您的权益,请联系删除! 文章目录 前言快速开始安装依赖权重下载及复原 训练网络数据集训练脚本 代码详解训练BaseOptio…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
