AVL树的完全指南:平衡与性能
文章目录
- AVL树简介
- AVL的操作
- 建立一个AVL树
- 插入操作
- 删除操作
- 书写代码
- 1.构造函数和析构函数
- 2.获取最大值和最小值
- 3.树的高度和节点个数
- 3.前序中序和后序遍历
- 4.判断树是否为空树
- 5.四个旋转操作
- 6.获取平衡因子
- 7.插入操作
- 8.删除操作
- 9.搜索节点
- .h文件中的定义
- 总结

AVL树简介
AVL树是一种自平衡的二叉搜索树,它的命名来源于其发明者 G. M. Adelson-Velsky 和 E. M. Landis。AVL树通过保持树的平衡性来提高搜索、插入和删除操作的效率。
在AVL树中,每个节点都有一个平衡因子,它表示节点的左子树高度与右子树高度的差值。平衡因子可以是-1、0或1,如果任何节点的平衡因子的绝对值大于1,则该树就不平衡,需要进行平衡调整。
AVL树本质也是一颗二叉查找树
但是在二叉查找树上加了平衡的概念,因为二叉查找树有很多限制的因素,当二叉查找树的节点呈线性分布的时候,整个二叉查找树就的效率就变成O(N),所以在AVL树中就不存在不平衡的情况。
1.AVL树的特点:
- 左子树和右子树的高度差不大于1。
- 左子树和右子树的子树也是一颗AVL树
2.AVL树的相关概念
- 平衡因子:
节点的平衡因子=左子树的高度-右子树的高度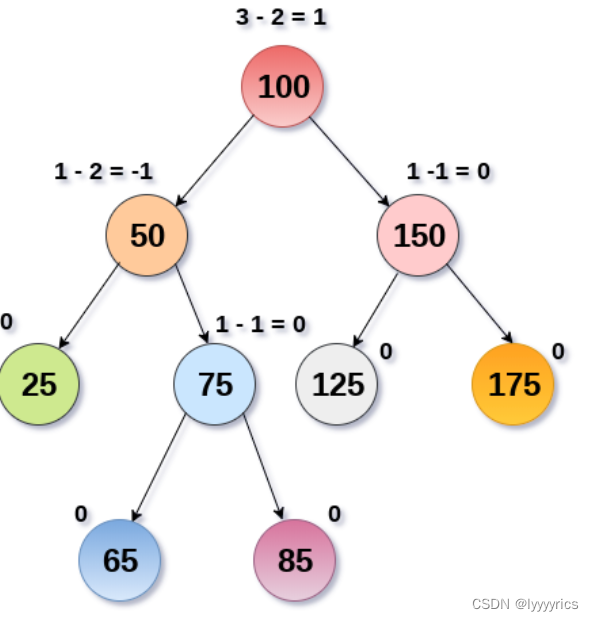
注意看上面的图上面的等式分别都代表了每个节点的平衡因子
3.AVL树对比普通二叉搜索树
2. 平衡性保证: AVL树保持了树的平衡性,即任何时刻树中任意节点的左右子树高度差不超过1。而普通的二叉搜索树可能会因为插入或删除操作而导致树的不平衡,从而影响了搜索、插入和删除操作的性能。
-
稳定的性能: 由于AVL树的平衡性,搜索、插入和删除操作的时间复杂度始终保持在 O(log n) 的水平,其中 n 表示树中节点的数量。而普通的二叉搜索树在最坏情况下可能会退化成链表,导致搜索、插入和删除操作的时间复杂度上升至 O(n)。
-
高效的搜索操作: AVL树的平衡性保证了树的高度始终保持在较小的范围内,使得搜索操作非常高效。而普通的二叉搜索树可能会因为不平衡而导致搜索操作的性能下降。
-
快速的插入和删除操作: AVL树的自平衡性保证了插入和删除操作的高效性,使得这些操作的时间复杂度始终为 O(log n)。而普通的二叉搜索树在插入或删除节点后可能需要进行额外的平衡调整操作,导致性能下降。
-
适用于高性能需求的场景: 由于AVL树在搜索、插入和删除操作上的高效性,它常被用作数据库中的索引结构,以提供快速的数据检索功能。而普通的二叉搜索树可能无法满足高性能的需求。
最直接的:

AVL的操作
建立一个AVL树
首先AVL树和二叉树一样,需要一个左子树和右子树的索引,还有需要一个存储值的关键字,除此之外,我们还需要保存当前节点的高度,因为在AVL树当中涉及到了高度之差,如果我们将当前节点的高度保存起来,就不用每次去计算了
代码:
class AVLNode
{friend class AVLTree;
public:private:AVLNode* _left;AVLNode* _right;int _key;int _height;
};class AVLTree
{
public:private:AVLNode* _root;
};
**这里我们用两个类来定义AVL树,比较方便,一个类定义节点,一个类维护节点
插入操作
当当前节点的平衡因子为0的时候,下一个值随便怎么插入都不会影响平衡,而当当前节点的平衡因子等于1的时候,下一个值插入的位置就会影响当前节点的平衡了,插入操作一共分为四种情况,我们一一介绍:
1.右旋
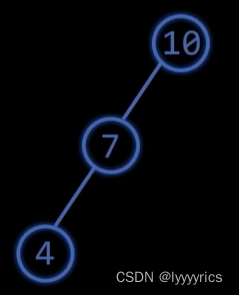
首先我们看上面这张图,当我们插入一个新的节点0时,很显然10的平衡因子是2,已经超过了AVL树定义的最大的平衡因子,所以,我们要对上面这颗树进行旋转让其满足AVL树的要求.
很显然,只需要将10右旋,然后让7作为10和4的新的父亲节点就可以了。
动图展示:

第二种需要右旋的情况:

这里只需要记住,,当我们要右旋时,冲突的右孩子作为新的左孩子就行了。
2.左旋
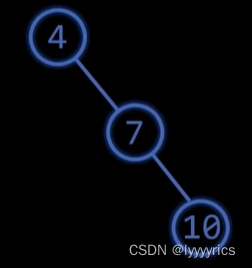
同样的,上面这个AVL树中的7的平衡因子的绝对值已经超过了1,所以应该对其进行旋转,由于4的平衡是-2,7的平衡因子是-1,,所以这种情况也被称之为RR型,对于这种RR型我们只需要对其进行一次右旋就可以解决问题了。
动图展示:

还有一种复杂的清情形:

先右旋再左旋
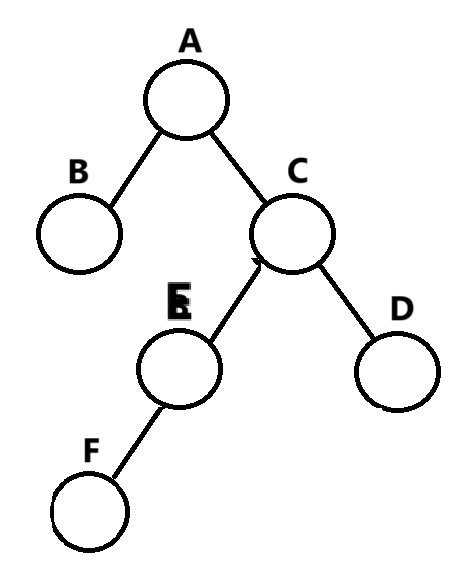
对于上面的AVL树,E是新插入的节点,首先这颗树的A节点的平衡因子是-2,然后就是C的平衡因子是1,这种情况我们把它叫做RL型,只需要对平衡因子是1的节点先进行右旋,然后再对平衡因子是A的节点进行左旋就可以了。
先左旋再右旋
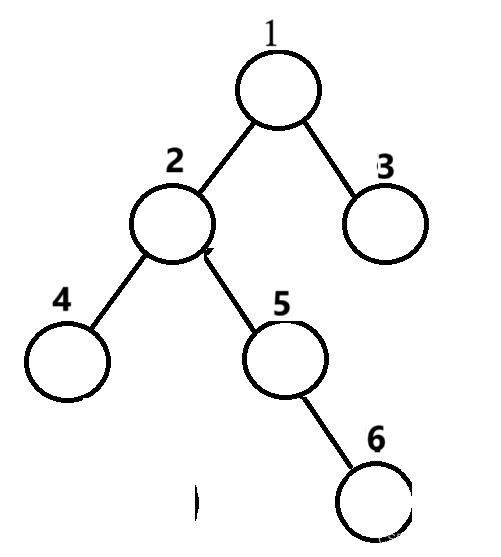
6是最后插入的节点对于这种情况,1的平衡因子是2,而2的平衡因子是-1.这种情况被称为是LR型,只需要先对平衡因子为-1的节点先左旋,然后再对平衡因子是2的节点进行右旋即可。
删除操作
删除操作和插入操作类似,再每次删除之后都要对祖先节点的平衡因子进行检查。
书写代码
1.构造函数和析构函数
//构造函数
AVLTree::AVLTree(AVLNode* root) :_root(root) {}//析构函数
AVLTree::~AVLTree()
{clear(_root);
}
void AVLTree::clear(AVLNode* node)
{if (node == nullptr){return;}clear(node->_left);clear(node->_right);delete node;
}
2.获取最大值和最小值
//获取最小值
int AVLTree::getMin()
{if (_root == nullptr){return INT_MIN;}AVLNode* root = _root;while (root->_left != nullptr){root = root->_left;}return root->_key;
}//获取最大值
int AVLTree::getMax()
{if (_root == nullptr){return INT_MAX;}AVLNode* root = _root;while (root->_right != nullptr){root = root->_right;}return root->_key;
}
//函数重载,用于返回节点
AVLNode* AVLTree::getMin(AVLNode* node)
{if (node == nullptr){return nullptr;}while (node->_left != nullptr){node = node->_left;}return node;
}
3.树的高度和节点个数
//获取AVL树的节点的个数
int AVLTree::AssistgetSize(AVLNode* root)
{if (root == nullptr){return 0;}return AssistgetSize(root->_left) + AssistgetSize(root->_right) + 1;
}
int AVLTree::getSize()
{return AssistgetSize(_root);
}
//获取高度
int AVLTree::getHeight()
{return AssistgetHeight(_root);
}
int AVLTree::AssistgetHeight(AVLNode* root)
{if (root == nullptr){return 0;}return root->_height;
}
3.前序中序和后序遍历
//中序遍历
void AVLTree::AssistinOrderTraversal(AVLNode* _root)
{if (_root == nullptr){return;}AssistinOrderTraversal(_root->_left);cout << _root->_key << ' ';AssistinOrderTraversal(_root->_right);
}
void AVLTree::inOrderTraversal()
{AssistinOrderTraversal(_root);
}//前序遍历
void AVLTree::preOrderTraversal()
{AssistpreOrderTraversal(_root);
}
void AVLTree::AssistpreOrderTraversal(AVLNode* root)
{if (root == nullptr){return;}cout << root->_key << ' ';AssistpreOrderTraversal(root->_left);AssistpreOrderTraversal(root->_right);
}
//后序遍历
void AVLTree::AssistpostOrderTraversal(AVLNode* root)
{if (root == nullptr){return;}AssistpostOrderTraversal(root->_left);AssistpostOrderTraversal(root->_right);cout << root->_key << ' ';
}
void AVLTree::postOrderTraversal()
{AssistpostOrderTraversal(_root);
}
4.判断树是否为空树
//判空
bool AVLTree::isEmpty()
{return _root == nullptr;
}
5.四个旋转操作
/左旋
void AVLTree::leftRotate(AVLNode*& node)
{AVLNode* right = node->_right;node->_right = right->_left;right->_left = node;node = right;
}
//右旋
void AVLTree::rightRotate(AVLNode*& node)
{AVLNode* left = node->_left;node->_left = left->_right;left->_right = node;node = left;
}
//先右旋再左旋
void AVLTree::rightleftRotate(AVLNode*& node)
{rightRotate(node->_right);leftRotate(node);
}
//先左旋再右旋
void AVLTree::leftrightRotate(AVLNode*& node)
{leftRotate(node->_left);rightRotate(node);
}
6.获取平衡因子
int AVLTree::getbalance(AVLNode* root)
{return AssistgetHeight(root->_left) - AssistgetHeight(root->_right);
}
7.插入操作
AVLNode* AVLTree::AssistInsert(int key, AVLNode*& node)
{if (node == nullptr){node = new AVLNode(key, nullptr, nullptr);return node;}else if (node->_key > key){AssistInsert(key, node->_left);//判断平衡因子是否是2,判断是LL型还是LR型if (getbalance(node) == 2){//LLif (getbalance(node->_left) == 1){//右旋rightRotate(node);}//LRelse{//先左旋再右旋leftrightRotate(node);}}}else if (node->_key < key){//向右边插入AssistInsert(key, node->_right);//如果是-2,那就是RR型或者是RL型if (getbalance(node) == -2){//RRif (getbalance(node->_right) == -1){//左旋leftRotate(node);}//RLelse{//先右旋再左旋rightleftRotate(node);}}}node->_height = max(AssistgetHeight(node->_left), AssistgetHeight(node->_right)) + 1;return node;
}void AVLTree::Insert(int key)
{_root = AssistInsert(key, _root);
}
8.删除操作
AVLNode* AVLTree::Assistremove(int key, AVLNode*& node)
{if (node == nullptr){//空节点不需要删除直接返回nullptrreturn nullptr;}//要删除的值小于当前节点的值if (node->_key > key){//递归左子树node->_left = Assistremove(key, node->_left);}//删除值大于当前节点的值else if (node->_key < key){//递归右子树node->_right = Assistremove(key, node->_right);}else{//1.左子树是空树,右子树和左子树都是空树if (node->_left == nullptr){AVLNode* tmp = node->_right;delete node;return tmp;}//只有右子树是空树的时候if (node->_right == nullptr){AVLNode* tmp = node->_left;delete node;return tmp;}//左子树和右子树都不是空树时else{//找到右子树的最小值节点AVLNode* min = getMin(node->_right);//赋值node->_key = min->_key;//将删除有左子树和右子树的节点转换为删除末尾的节点node->_right = Assistremove(min->_key, node->_right);}}node->_height = max(AssistgetHeight(node->_left), AssistgetHeight(node->_right)) + 1;int balance = getbalance(node);if (balance == 2){if (getbalance(node->_left) == 1){rightRotate(node);}else{leftrightRotate(node);}}else if (balance == -2){if (getbalance(node->_right) == -1){leftRotate(node);}else{rightleftRotate(node);}}return node;
}
void AVLTree::remove(int key)
{_root = Assistremove(key, _root);
}
9.搜索节点
//搜索
bool AVLTree::search(int key, AVLNode* node)
{if (node == nullptr){return false;}if (node->_key == key){return true;}if (node->_key > key){return search(key, node->_left);}else{return search(key, node->_right);}
}
bool AVLTree::search(int key)
{return search(key, _root);
}
上面的代码对照着图理解更容易理解
.h文件中的定义
class AVLNode
{friend class AVLTree;
public:AVLNode(int key, AVLNode* left, AVLNode* right, int hight = 0){_key = key;_left = left;_right = right;_height = hight;}
private:AVLNode* _left;AVLNode* _right;int _key;int _height;
};class AVLTree
{
public:AVLTree(AVLNode* root = nullptr);~AVLTree();int getbalance(AVLNode* root);AVLNode* AssistInsert(int key, AVLNode*& node);void Insert(int key);void leftRotate(AVLNode*& node);void rightRotate(AVLNode*& node);void rightleftRotate(AVLNode*& node);void leftrightRotate(AVLNode*& node);AVLNode* Assistremove(int key, AVLNode*& node);void remove(int key);bool search(int key);bool search(int key, AVLNode* node);int getMin();AVLNode* getMin(AVLNode* node);int getMax();int AssistgetHeight(AVLNode* root);int getHeight();void inOrderTraversal();void AssistinOrderTraversal(AVLNode* _root);void preOrderTraversal();void AssistpreOrderTraversal(AVLNode* _root);void postOrderTraversal();void AssistpostOrderTraversal(AVLNode* _root);int getSize();int AssistgetSize(AVLNode* root);void clear(AVLNode* node);bool isEmpty();
private:AVLNode* _root;
};
总结
在本篇博客中,我们深入探讨了 AVL 树这一经典的数据结构。AVL 树作为一种自平衡的二叉搜索树,通过保持树的平衡性,提供了高效的搜索、插入和删除操作。我们从 AVL 树的基本概念出发,介绍了它的定义、特性和基本操作,包括旋转操作和平衡因子的概念。通过具体的例子和图示,我们深入理解了 AVL 树的工作原理和算法设计。
AVL 树之所以如此重要和受欢迎,主要是因为它在各种应用中都具有突出的优势。无论是作为数据库索引、编译器中的符号表还是操作系统中的文件系统,AVL 树都能够提供高效的数据检索功能,保证了程序的性能和效率。通过学习和掌握 AVL 树,我们不仅可以解决实际问题,提高程序的性能,还能够深入理解和应用其他复杂数据结构,为我们的编程技能和软件工程能力增添新的高度。
希望通过本篇博客的阅读,读者能够对 AVL 树有一个更加深入的理解,并且能够将其应用到实际的项目中去,为软件开发和数据处理带来更大的价值。感谢大家的阅读和支持!
相关文章:
AVL树的完全指南:平衡与性能
文章目录 AVL树简介AVL的操作建立一个AVL树插入操作删除操作 书写代码1.构造函数和析构函数2.获取最大值和最小值3.树的高度和节点个数3.前序中序和后序遍历4.判断树是否为空树5.四个旋转操作6.获取平衡因子7.插入操作8.删除操作9.搜索节点.h文件中的定义 总结 AVL树简介 AVL树…...

itext7 PDF添加水印,获取页面高度,添加到页面右上角
ps: pdf添加水印,内容多的时候会往下跑,修改为获取当前页面高度,进行固定在顶部,其他需要可以自己进行调整,直接贴代码。 public static void main(String[] args) throws IOException {String localFilePath "…...
docker端口映射成功,docker端口不生效的问题解决,外界无法访问docker映射端口
docker端口映射不生效的问题解决 问题 使用docker run -p 88848:8848后,显示容器启动正常,并且使用docker logs –f xxx能够看到容器可以正常启用,docker ps 可以看到容器启动成功,并且端口已经映射,但是在浏览器访问相关地址&am…...

RSA非对称加密解密,前端公钥加密后端私钥解密
RSA非对称加密解密,前端公钥加密后端私钥解密,可以防止陌生人直接通过后端接口篡改数据。有数据泄露的风险。 前端:Vue框架 后端:sprintboot(Java) 工具类:hutool 前端Vue获取公钥:…...

Nginx-01-Nginx 是什么? 能做什么?
nginx 系列 Nginx-01-聊一聊 nginx Nginx-01-Nginx 是什么 Nginx-02-为什么使用 Nginx Nginx-02-Nginx Ubuntu 安装 windows10 WSL ubuntu 安装 nginx 实战笔记 Nginx-02-基本使用 Nginx-03-Nginx 项目架构 Nginx-04-Docker Nginx Nginx-05-nginx 反向代理是什么&…...

最大数字——蓝桥杯十三届2022国赛大学B组真题
问题分析 这道题属于贪心加回溯。所有操作如果能使得高位的数字变大必定优先用在高位,因为对高位的影响永远大于对低位的影响。然后我们再来分析一下,如何使用这两种操作?对于加操作,如果能使这一位的数字加到9则变成9࿰…...
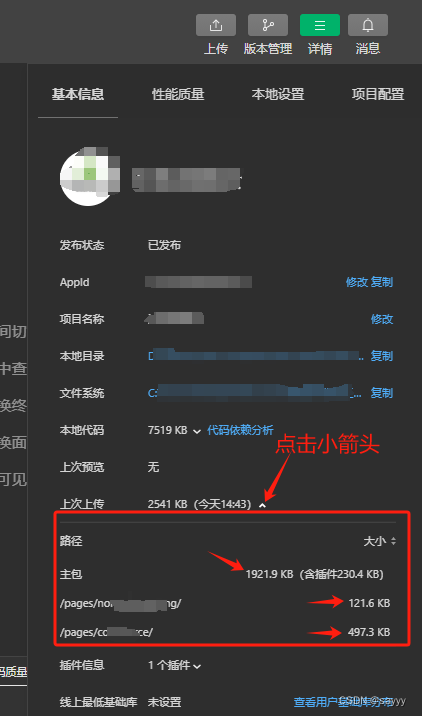
查看微信小程序主包大小
前言 略 查看微信小程序主包大小 在微信开发者工具右上角找到“详情->基本信息” 查看微信小程序主包构成 通过微信开发者工具中的“代码依赖分析”工具查看...

B树与B+树的奥秘:原理解析与性能
引言 B树和B树是计算机科学中两个重要的数据结构,它们在数据库和文件系统中扮演着至关重要的角色。在处理大量数据时,高效的数据组织和检索方式是至关重要的,而B树和B树正是为此而设计的。 B树和B树都是多路查找树的变体,它们通…...

Unity组件入门篇目录
Audio AudioChorusFilter......................................点击导航AudioDistortionFilter..................................点击导航AudioEchoFilter.........................................点击导航AudioHighPassFilter..................................点击导…...

【Python技术】使用akshare、pandas高效复盘每日涨停板行业分析
作为一个程序员宝爸,每天的时间很宝贵,工作之余除了辅导孩子作业,就是补充睡眠。 怎么快速高效的进行当天A股涨停板的复盘,便于第二天的跟踪。这里简单写个示例, 获取当天连涨数排序,以及所属行业排序。 …...
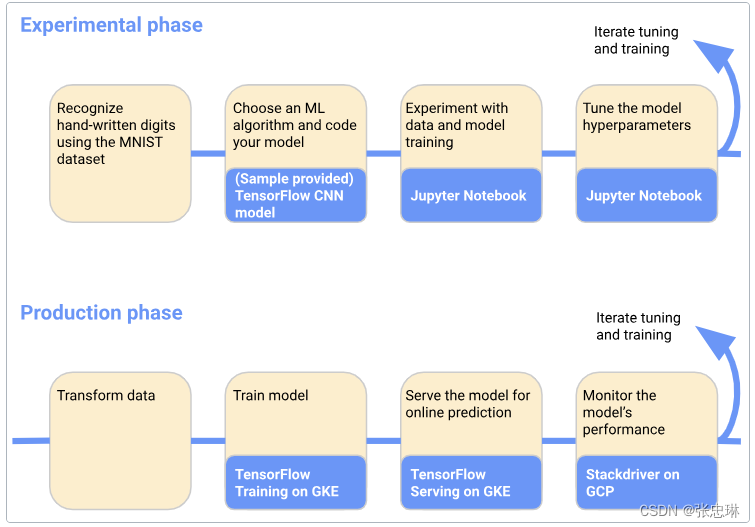
kubeflow文档-介绍与架构
1. kubeflow介绍 Kubeflow项目致力于使机器学习(ML)工作流在Kubernetes上的部署变得简单、可移植和可扩展。目标不是重新创建其他服务,而是提供一种直接的方法,将ML的开源系统部署到不同的基础设施中。无论在哪里运行Kubernetes&a…...

传输层的TCP流量控制比数据链路层作用范围更广
数据链路层的流量控制主要在相邻节点之间进行,它确保在单个链路或网络段上不会发生数据过载。例如,在以太网中,数据链路层使用停止-等待协议或滑动窗口机制来限制发送方发送的数据量,以避免接收方无法处理数据。 而传输层的 TCP 流…...

CSS表格
标准的表格结构 table标签:定义表格 caption标签:定义表格标题,这个标题会居中显示在表格上,一个表格只能定义一个标题 th标签:定义表格的表头,通常成粗体居中表示 tr标签:定义表格的一行 td标…...

东芝移动硬盘数据恢复方法有哪些
谁能懂我此刻的心情啊!移动硬盘用起来真的超级方便,如今我的工作几乎都离不开它,用来存放各种重要文件。可是,让人头疼的事情发生了,昨天我发现移动硬盘里的部分数据竟然莫名其妙地消失了!这可咋整啊&#…...

FullCalendar日历组件集成实战(1)
背景 有一些应用系统或应用功能,如日程管理、任务管理需要使用到日历组件。虽然Element Plus也提供了日历组件,但功能比较简单,用来做数据展现勉强可用。但如果需要进行复杂的数据展示,以及互动操作如通过点击添加事件࿰…...
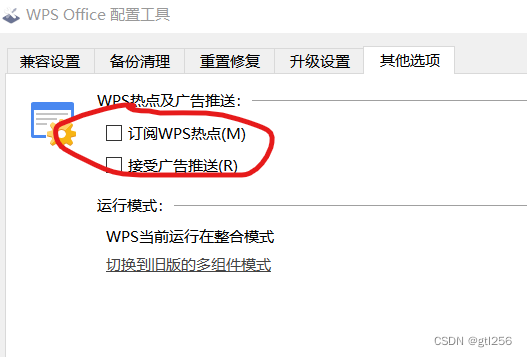
wps
文章目录 取消自动升级、WPS热点及广告推送excel数字大小排序函数不起作用vlookup函数 取消自动升级、WPS热点及广告推送 打开WPS Office,点击左上角“首页”图标,依次点击右上角“设置”—>“配置和修复工具”。在弹出框点击“高级”,选…...
【软设】常见易错题汇总
目录 计算机系统基础 程序语言基础 数据结构 算法设计与分析 计算机网络与信息安全 软件工程基础 开发方法(结构化与面向对象) 数据库 操作系统 知识产权相关的法律法规 🤯🤯🤯🤯🤯ǹ…...

安全数据交换系统哪个好?该如何选型?
安全数据交换系统是用于在不同网络或组织之间安全、高效地传输和共享数据的解决方案。安全数据交换系统对于任何需要处理敏感数据、确保数据安全、并满足合规要求的组织来说都是至关重要的。 这种系统通常用于以下目的: 1)数据传输:允许用户…...
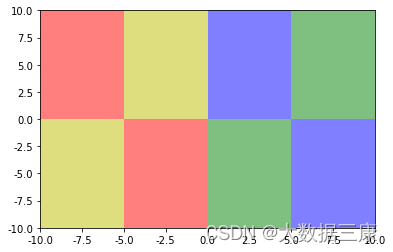
用matplotlib制作代码和色块
代码如下: # 声明 # -*- coding: utf-8 -*- """ Created on Mon May 13 11:18:59 2024author: sankang """ # 这里调用包 import matplotlib as mpl import matplotlib.pyplot as plt import numpy as npplt.rcParams[axes.unicode_…...

centos无法tab补全至文件
很奇怪的需求:redhat 7.9版本用cd 只能到目录,无法到文件 我个人认为不是个问题,但是甲方需求,你懂的 首先,我们要搞清楚tab补全功能的包bash-completion是否安装,这里肯定是安装了,不过还是看…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
