算法练习第22天|39. 组合总和、40.组合总和II
39. 组合总和
39. 组合总和 - 力扣(LeetCode)![]() https://leetcode.cn/problems/combination-sum/description/
https://leetcode.cn/problems/combination-sum/description/
题目描述:
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates =[2,3,6,7],target =7输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: [] 提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
思路分析:
由于所有candidates的数>=1,所以不必担心有0的问题。另外,由于元素可以多次使用,所以其搜索过程对应的树形结构如下所示:
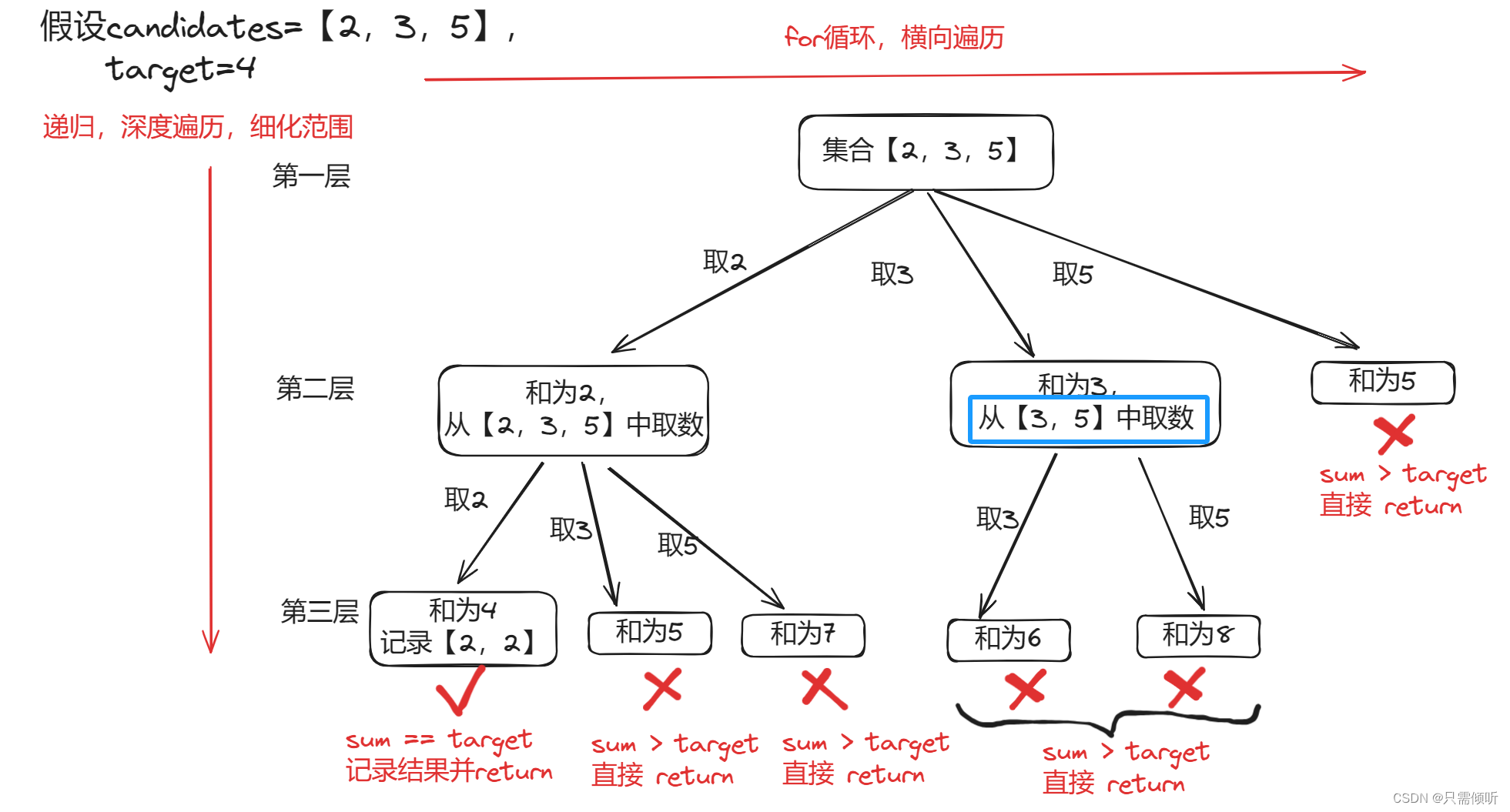
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回! 另外,注意蓝色框中文字,因为要求的是满足条件的
下面我们结合上述的树形结构图,按照回溯三部曲来尝试书写代码:
- 回溯第一步:确认回溯函数的参数和返回值。
这里依然是定义两个全局变量,二维数组result存放结果集,数组path存放符合条件的结果。(这两个变量可以作为函数参数传入)
老规矩,返回值类型void。参数除了题目所给的数组candidates以及目标和target之外,为了方便理解,我们算法练习第21天|216.组合总和|||、17.电话号码的字母组合-CSDN博客中的216.组合总和|||的解法一样,添加了目前路径上所遍历的元素的和sum以及开始遍历的位置startIndex。
可能有人有人会有疑问,为什么在17.电话号码的字母组合这一题中没有写startIndex?对于组合问题,什么时候需要startIndex呢?下面给出startIndex的使用场景:
如果是从一个集合中求组合的话,就需要startIndex,例如算法练习第20天|回溯算法 77.组合问题 257. 二叉树的所有路径-CSDN博客中的77.组合问题,以及上述的216.组合总和|||。
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex,例如:上面的17.电话号码的字母组合。
所以本题要求是从同一个集合中求组合,所以要用到startIndex。至于具体怎么用,下面代码中在细说。
回溯函数大致长这样:
vector<vector<int>> result;
vector<int> path;
//回溯第一步,确定回溯函数的参数和返回类型
void backTracking(vector<int>& candidates, int target, int sum, int startIndex){}- 回溯函数第二步:确认回溯终止条件
从下面的树形结构可知, 回溯的终止条件只有 sum== targeth和sum > target两种。如果是sum<target,则说明还有继续寻找并添加元素的可能,所以这种要执行的是单层回溯的逻辑。
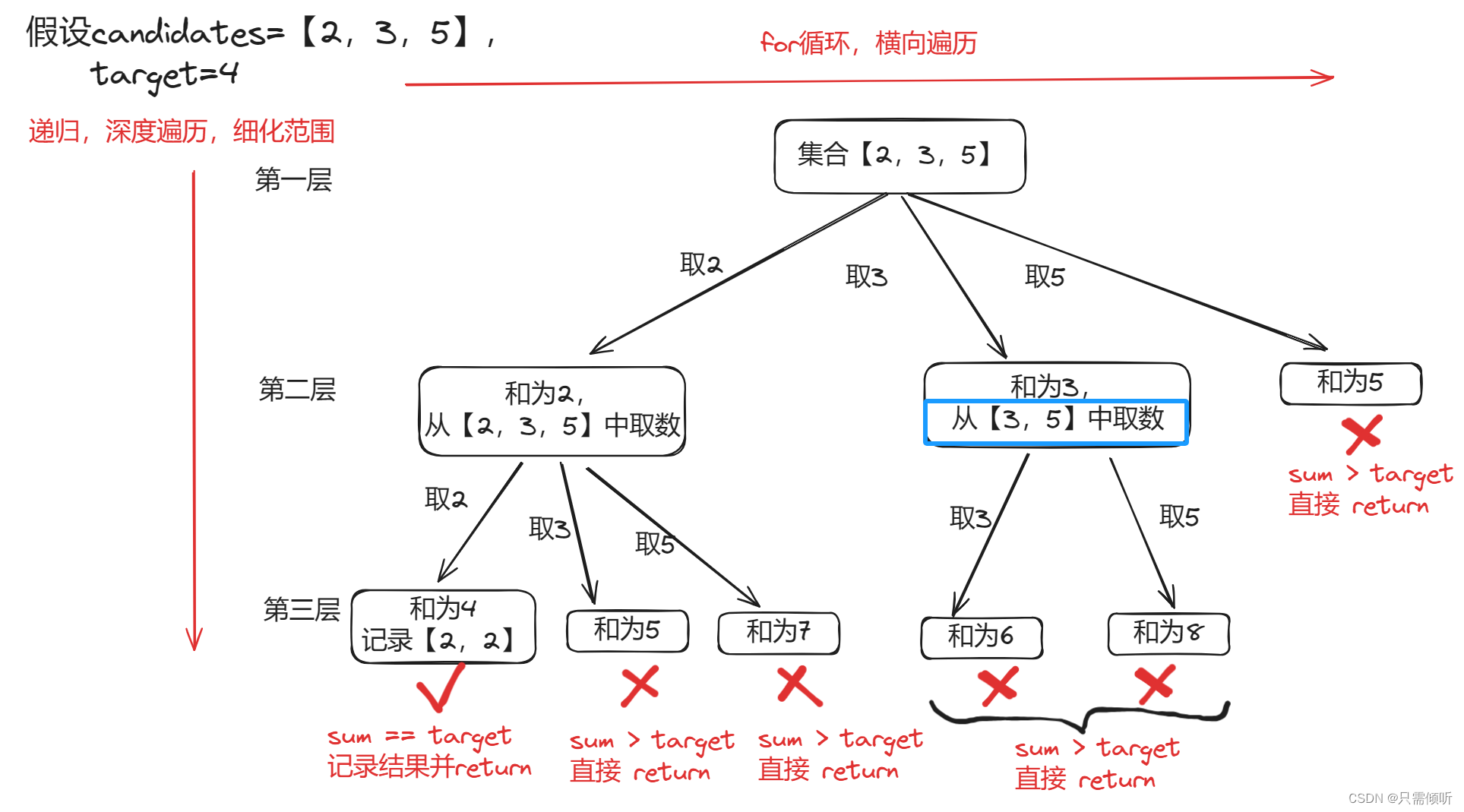
所以回溯终止条件长这样:
//回溯第二步,确定回溯终止条件
if(sum == target){result.push_back(path);return;
}
else if(sum > target){return;
}- 回溯第三步:确认单层搜索逻辑
能到达这一步,表明sum<target,需要继续进行元素搜索。因此,要做的操作有处理节点(sum加上当前节点,path中记录当前节点),然后就该执行递归了,接着是回溯。代码如下:
//回溯第三步,确认当层回溯逻辑,并回溯
for(int i = startIndex; i < candidates.size(); i++){sum += candidates[i]; //处理节点path.push_back(candidates[i]);backTracking(candidates, target, sum, i); //递归sum -= candidates[i]; //回溯path.pop_back();}这里我们用到了startIndex,注意我们在递归时的给最后一个参数传的是i,程序初始时传的startIndex肯定为0,所以i最开始为0。但是搜索完最左侧的大分支后,该记录的结果记录下来,该回溯的回溯,i++变成了1,结合下图,为了避免上面所说的【2,3】和【3,2】的组合重复,所以取数时变成了从【3,5】中取数,这就导致startIndex也需要有更新。那么更新为多少时何时呢?观察下图可知当startIndex和此时的i一样时就满足了从【3,5】中取数的条件,于是我们在递归时把i作为了第四个参数的实参。
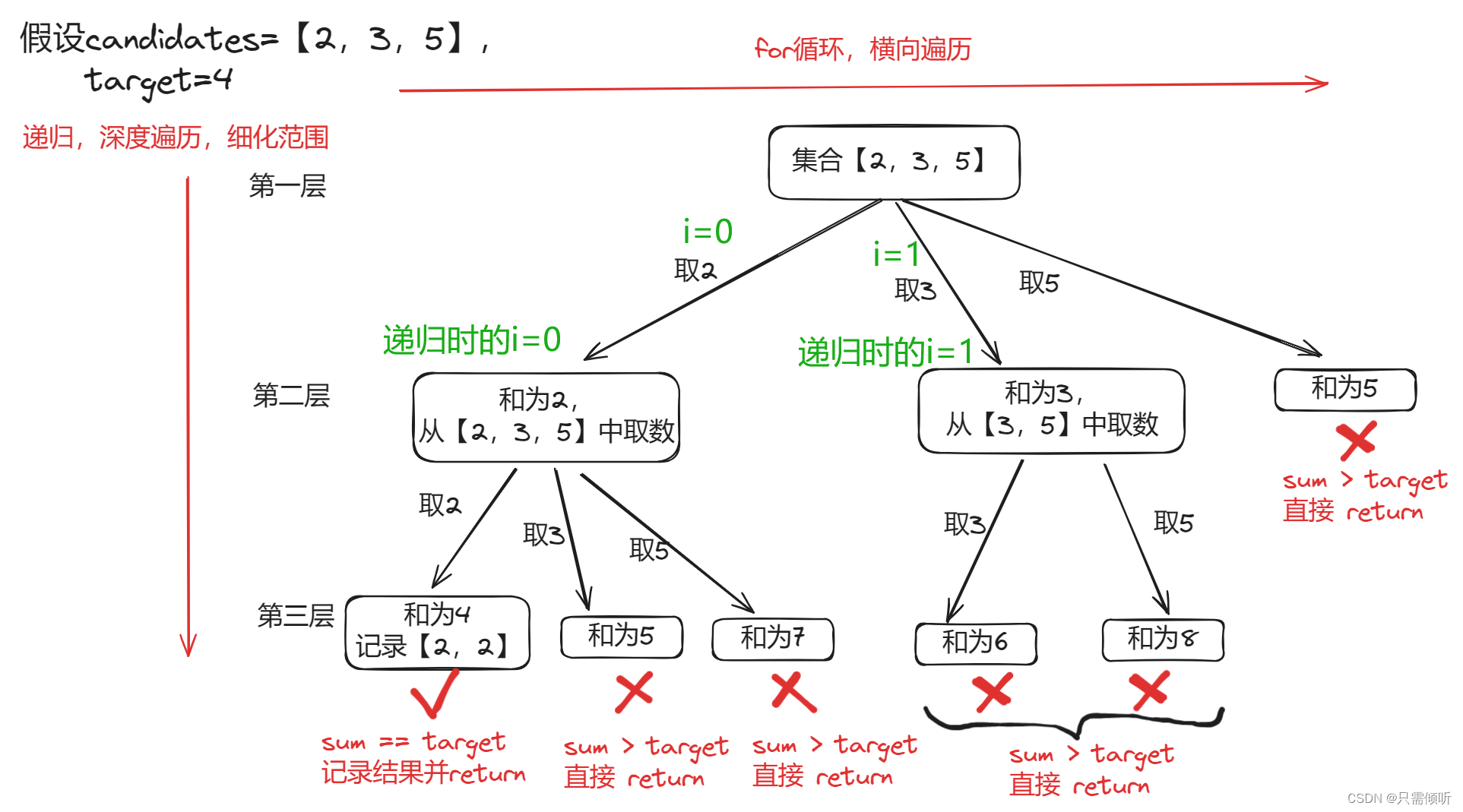
整体代码:
整体代码的书写如下:
class Solution {
public:vector<vector<int>> result;vector<int> path;//回溯第一步,确定回溯函数的参数和返回类型void backTracking(vector<int>& candidates, int target, int sum, int startIndex){//回溯第二步,确定回溯终止条件if(sum == target){result.push_back(path);return;}else if(sum > target){return;}//回溯第三步,确认当层回溯逻辑,并回溯for(int i = startIndex; i < candidates.size(); i++){sum += candidates[i]; //处理节点path.push_back(candidates[i]);backTracking(candidates, target, sum, i); //递归sum -= candidates[i]; //回溯path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backTracking(candidates,target,0,0);return result; }
};40.组合总和II
40. 组合总和 II - 力扣(LeetCode)![]() https://leetcode.cn/problems/combination-sum-ii/description/
https://leetcode.cn/problems/combination-sum-ii/description/
题目描述:
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates =[10,1,2,7,6,1,5]target =8输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]
提示:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
本人看完解法也不太理解,哎,先放着。。。。
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序,让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};相关文章:
算法练习第22天|39. 组合总和、40.组合总和II
39. 组合总和 39. 组合总和 - 力扣(LeetCode)https://leetcode.cn/problems/combination-sum/description/ 题目描述: 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数…...

CCF PTA 2022年11月C++大富翁游戏
【问题描述】 小明很喜欢玩大富翁游戏,这个游戏的规则如下: 1、游戏地图是有 N 个格子,分别编号从 1 到 N。玩家一开始位于 1 号格子。 2、地图的每个格子上都有事件,事件有以下两种类型: A)罚款 x 枚金币…...

React获取form表单值的N种方式
Ref模式(非受控模式) 非钩子模式 1.createRef()方式 js: userNameElcreateRef() <input type"text" name"userName" ref{this.userNameEl} /> 获取值的方式: this.userNameEl.current.value2.refs(废弃) js: con…...
Apache Knox 2.0.0使用
目录 介绍 使用 gateway-site.xml users.ldif my_hdfs.xml my_yarn.xml 其它 介绍 The Apache Knox Gateway is a system that provides a single point of authentication and access for Apache Hadoop services in a cluster. The goal is to simplify Hadoop securit…...

Tomcat 内核详解 - Web服务器机制
详细介绍 Apache Tomcat 是一个开源的Web服务器和Servlet容器,它实现了Java Servlet、JavaServer Pages (JSP) 和WebSocket规范。Tomcat的核心设计围绕着几个关键组件,它们共同构成了处理HTTP请求、管理Web应用部署和执行Servlet逻辑的基础架构。 Apac…...

几个人脸库对于面部动作识别的功能比较
经粗略研究,insightface只能识别面部特征点的位置,根据这些位置不能直接推出一个人是否在睡觉。 OpenFace 是一个高级的面部行为分析工具,它能够识别和分析多种面部动作单位(Facial Action Coding System, FACS),这些动作单位是根据面部肌肉活动定义的。每个动作单位(A…...
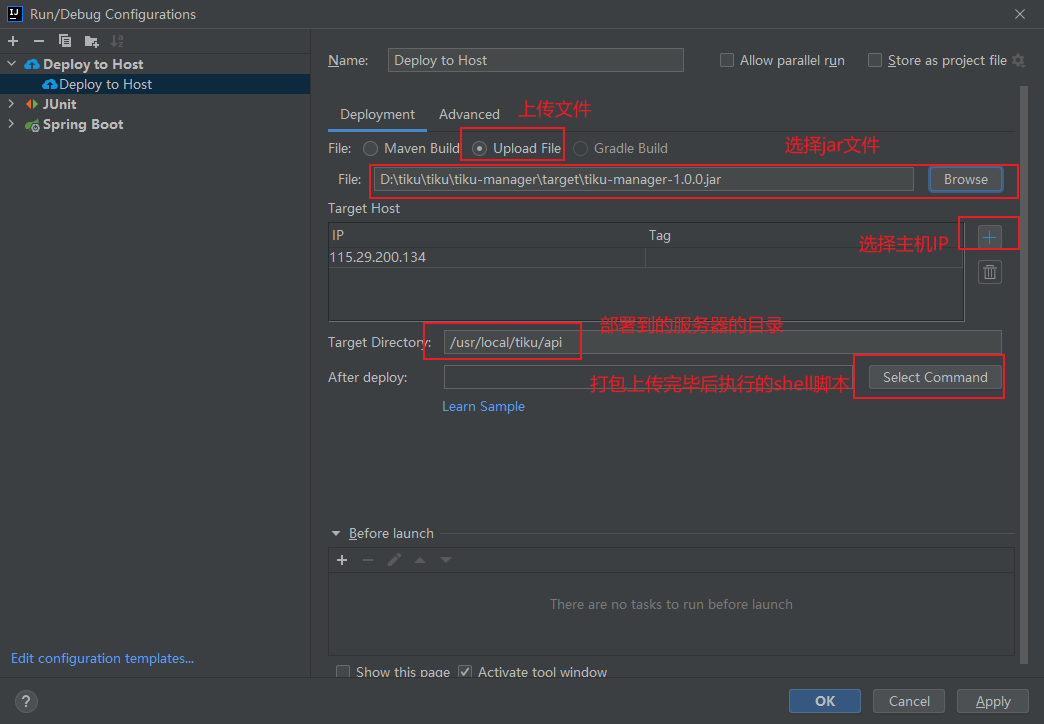
IDEA 使用Alibaba Cloud Toolkit 实现远程 自动部署
安装插件 maven方式部署 配置服务器主机信息 配置发布到主机 单击Select 单击run 就可以将选择module的jar文件上传到服务器的指定位置了 Alibaba Cloud Toolkit 上传文件的方式部署...

蓝桥杯备战15.完全二叉树的权值
P8681 [蓝桥杯 2019 省 AB] 完全二叉树的权值 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) #include<bits/stdc.h> using namespace std; #define endl \n #define int long long const int N 2e510; int a[N]; signed main() {std::ios::sync_with_stdio(0),cin.ti…...

【前端】LayUI监听事件汇总
一、监听单选按钮事件 点击资源类型单选按钮时,请求后台接口,把接口返回的内容追加到选择资源下拉框内 HTML <div class"layui-form-item"><label class"layui-form-label">资源类型:</label><d…...
)
【多电压流程 Multivoltage Flow】- 5.特定工具使用建议(1.VCS NLP VC LP)
本章提供了关于使用Synopsys工具进行低功耗设计和分析的信息。它包含以下部分: • 使用VCS NLP和VC LP进行多电压验证 • 使用Design Compiler进行逻辑综合 • 使用IC Compiler进行设计规划 • 使用IC Compiler进行物理实现 • 使用IC Compiler II和Fusion Compiler进行物…...
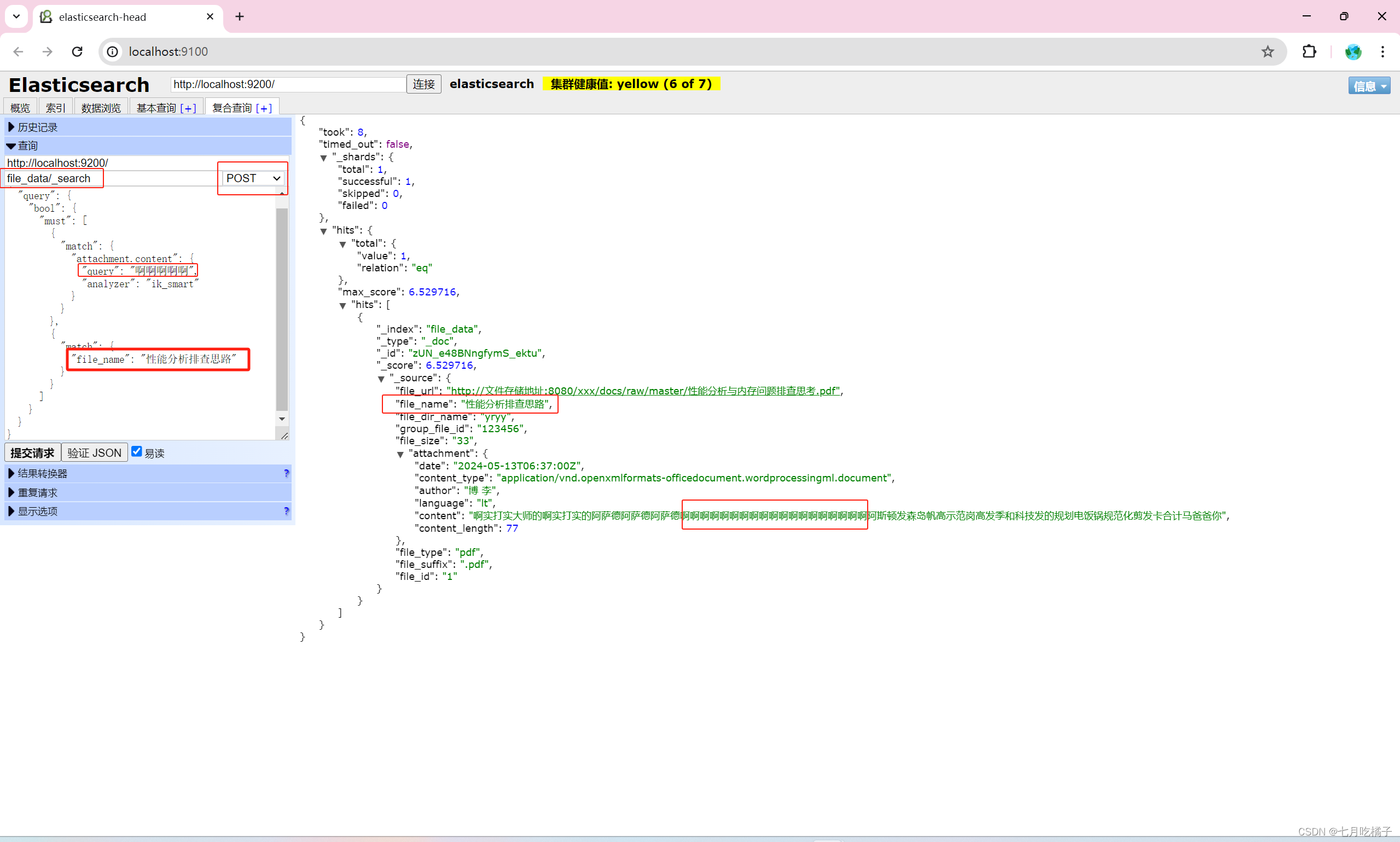
Elasticsearch 实现word、pdf、txt、excel文档内容快速检索(保姆级教程)
本文主要讲解ES如何从提取文档中提取内容(word、pdf、txt、excel等文件类型),实现快速检索文档内容实现。 特别说明一下,为什么用7.10.0版本,因为在项目中除了精确匹配的要求,也会有模糊查询(关…...

[初学rust] 04_rust复合类型
rust复合类型 字符串 由于rust的字符串元素类型是u8(1字节),但是字符类型是unicode(4字节) 索引不能像C那样读取又由于String类型和&str类型都是utf-8编码,中文占3字节切片可能会导致崩溃 slice(切片) 切片就是对String类型中的一部分的引用,它…...

什么是Zoho CRM客户关系系统管理?
以客户为中心的商业时代,卓越的客户体验已成为企业持续增长与成功的关键,为了在这场激烈的市场竞争中脱颖而出,企业需要一套强大、灵活且智能的客户关系管理系统——Zoho CRM应运而生,它不仅是管理客户信息的工具箱,更是驱动业务增…...

青岛东软载波子公司东软载波微电子授权世强硬创代理,出货量累计超20亿颗
凭借业内独特的互联网推新模式,世强先进(深圳)科技股份有限公司(下称“世强先进”) 获得本土工业MCU企业——上海东软载波微电子有限公司(下称“东软载波微电子”,英文:essemi&#…...
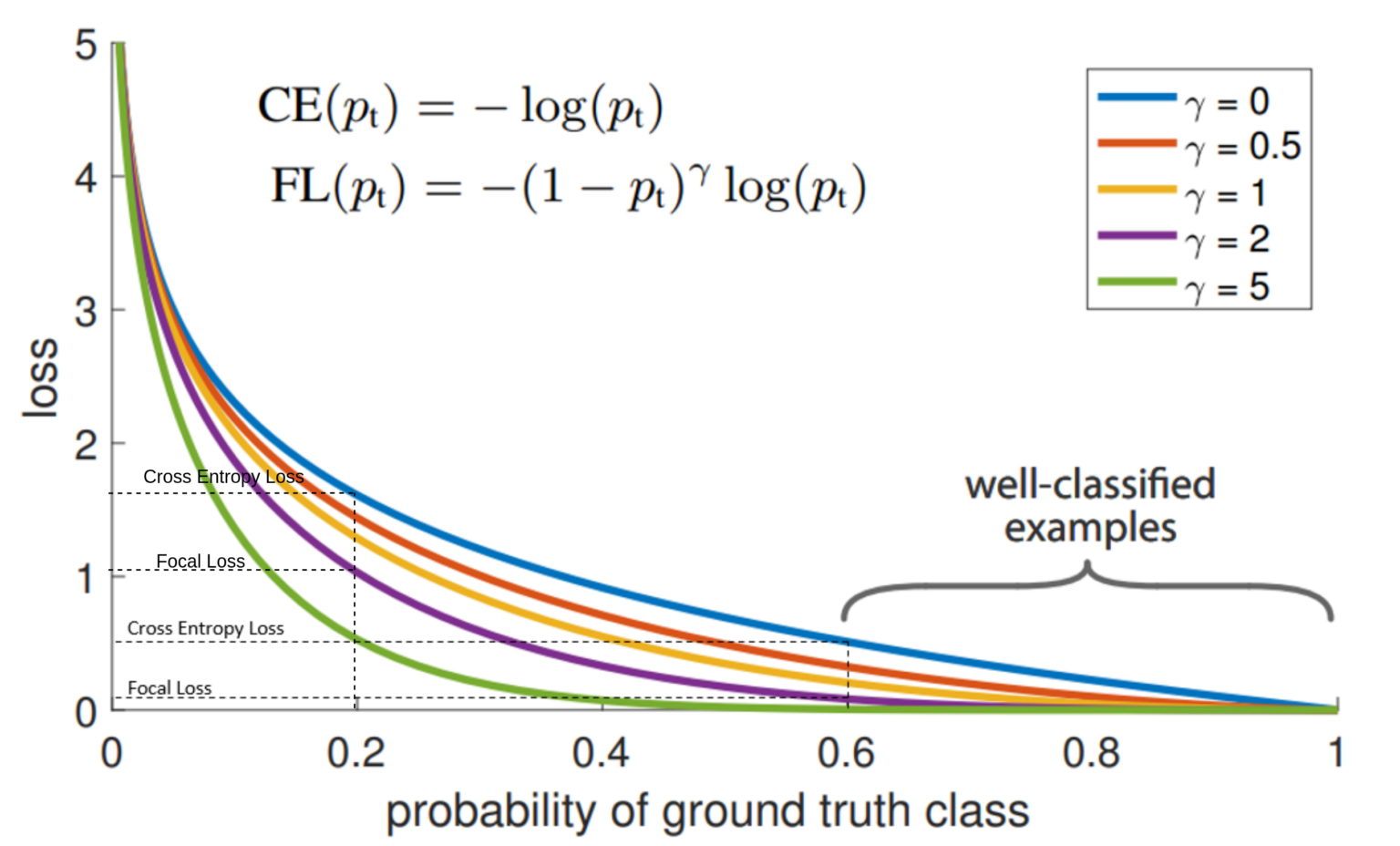
YOLO损失函数——SIoU和Focal Lossr损失函数解析
1. 概述 YOLO(You Only Look Once) 系列模型以其实时目标检测能力而闻名,其有效性在很大程度上归功于其专门设计的损失函数。在本文中,这里将深入探讨YOLO演进中不可或缺的各种YOLO损失函数,并重点介绍它们在PyTorch中…...

C++:编程世界的永恒之石
在编程的广袤领域中,C犹如一块永恒的基石,历经岁月的洗礼,依旧坚固而璀璨。它的深厚底蕴、强大功能和广泛的应用领域,使其成为无数程序员心中的信仰与追求。 一、C:历史与传承的交汇点 C的历史可追溯到上世纪80年代&…...

线上3D博物馆搭建简单吗?有何优势?有哪些应用场景?
随着科技的飞速发展,传统的博物馆参观方式正在经历一场前所未有的变革,在科技的“加持”下,不少博物馆凭借强大的技术、创意和美学实践,频频“出圈”,线上3D博物馆逐渐崛起,这不仅丰富了人们的文化体验&…...

Rust 语言的“命名空间” —— mod
在Rust中,虽然没有像C中的namespace这样的显式关键字,但是Rust通过模块(mod)系统提供了一种类似命名空间的功能。模块允许你将相关的代码组织在一起,并可以通过pub关键字来控制哪些项(如函数、结构体、枚举…...

加速科技突破2.7G高速数据接口测试技术
随着显示面板分辨率的不断提升,显示驱动芯片(DDIC)的数据接口传输速率越来越高,MIPI、LVDS/mLVDS、HDMI等高速数据接口在DDIC上广泛应用。为满足高速数据接口的ATE测试需求,作为国内少数拥有完全自研的LCD Driver测试解…...

从0开始搭建一个react项目 第一 二 三天
从0开始搭建一个react项目 今天接到一个任务让我把原来用ext.js写的前端换成react写的,我好慌的,因为我就是一个小白,之前只做过简单的二次开发功能。唉,我只是一个领着微薄薪水的小实习生,为什么要有这个任务&#x…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
