【动态规划五】回文串问题
目录
leetcode题目
一、回文子串
二、最长回文子串
三、分割回文串 IV
四、分割回文串 II
五、最长回文子序列
六、让字符串成为回文串的最少插入次数
leetcode题目
一、回文子串
647. 回文子串 - 力扣(LeetCode)![]() https://leetcode.cn/problems/palindromic-substrings/1.题目解析
https://leetcode.cn/problems/palindromic-substrings/1.题目解析
返回给定字符串中所有回文子串的个数
2.算法分析
1.状态表示
如果是暴力解法,只需要先固定下标i, 然后j从i的位置开始往后一路枚举即可,下一次i++, j无需回到0号下标,因为[i, j]与[j, i]本质是同一个子串,j直接从i位置开始枚举即可, 因此我们就把状态表示定义成二维的~
dp[i][j]: s字符串中位于区间 [i, j] 的字符串, 是否是回文串 (隐含条件: i <= j)
2.状态转移方程
3.初始化
初始化的目的是 保证填表时不越界 + 后续填表是正确的
4.填表顺序
填dp[i][j]时,需要dp[i+1][j-1]的值,因此需要从下往上填每一行即可
5.返回值
返回dp表中值为true的个数即可
3.算法代码
class Solution {
public:int countSubstrings(string s) {//1.创建dp表int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n, false));//2.填表+返回值int sum = 0;for(int i = n-1; i >= 0; i--) //从下往上填表{for(int j = i; j < n; j++){if(s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;if(dp[i][j]) sum++; }}return sum;}
};二、最长回文子串
5. 最长回文子串 - 力扣(LeetCode)![]() https://leetcode.cn/problems/longest-palindromic-substring/1.题目解析
https://leetcode.cn/problems/longest-palindromic-substring/1.题目解析
返回给定字符串中的最长回文子串
2.算法分析
求最长回文子串之前,先要知道哪些字符串是回文串,而题目一通过dp表,记录了[i, j]子串是否是回文串,根据dp表的值即可得到想要的结果
3.算法代码
class Solution {
public:string longestPalindrome(string s) {//1.创建dp表int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n, false));//2.填表+返回值int begin = 0, len = 0;for(int i = n-1; i >= 0; i--) //从下往上填表{for(int j = i; j < n; j++){if(s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true;//更新结果if(dp[i][j] && len < j - i + 1) {len = j - i + 1;begin = i;}}}return s.substr(begin, len);}
};三、分割回文串 IV
1745. 分割回文串 IV - 力扣(LeetCode)![]() https://leetcode.cn/problems/palindrome-partitioning-iv/1.题目解析
https://leetcode.cn/problems/palindrome-partitioning-iv/1.题目解析
判断给定的字符串是否能够分割成三个回文字符串, 返回true/false
2.算法分析
本题的关键就是看给定字符串能否被分割成三个回文子串, 也就是判断[0, i-1], [i, j], [j+1, n-1]这三个区间的字符串是否是回文子串,而题目一中我们用动态规划做到了使用dp表保存所有的子串是否是回文信息,因此用o(1)的时间复杂度判断即可
3.算法代码
class Solution {
public:bool checkPartitioning(string s) {//1.创建dp表int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n, false));//2.填表for(int i = n-1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])dp[i][j] = i + 1 < j ? dp[i+1][j-1] : true; //3.返回值for(int i = 1; i < n - 1; i++) //第二个字符串的开始for(int j = i; j < n - 1; j++) //第二个字符串的结束if(dp[0][i-1] && dp[i][j] && dp[j+1][n-1])return true;return false;}
};四、分割回文串 II
132. 分割回文串 II - 力扣(LeetCode)![]() https://leetcode.cn/problems/palindrome-partitioning-ii/本题与 139. 单词拆分 - 力扣(LeetCode) 这道题目非常类似,大家可以对比一下两道题的做法
https://leetcode.cn/problems/palindrome-partitioning-ii/本题与 139. 单词拆分 - 力扣(LeetCode) 这道题目非常类似,大家可以对比一下两道题的做法
【动态规划三】子数组系列-CSDN博客文章浏览阅读803次,点赞20次,收藏21次。f[i]:以 i 位置为结尾的所有子数组中,最后呈现 "上升" 状态下的最长的湍流子数组的长度。g[i]:以 i 位置为结尾的所有子数组中,最后呈现 "下降" 状态下的最长的湍流子数组的长度。数组中相邻元素对之间的大小关系相反,这就是湍流数组,题目要求返回数组中最长的湍流子数组的长度。将dp表里面所有的值都初始化成1, 因此dp[i] += dp[i-1] 即可。dp[i]: [0, i]区间内的字符串, 能否被字典中的单词拼接而成。dp[i] 表示 以 i 位置元素为结尾的所有子数组的最大和。https://blog.csdn.net/m0_74126249/article/details/138501298?spm=1001.2014.3001.55011.题目解析
给定字符串s,将s分割,使得每个部分都是回文子串,求最少的分割次数
2.算法分析
1.状态表示
dp[i] 表示 [0, i] 区间上的字符串, 分割成回文串的最少分割次数
2.状态转移方程
而本题目要频繁的用到判断一个字符串是否是回文,因此用到题目一的做法,把所有子串是否是回文的信息,保存在dp表中
3.初始化
j > 0, 所以填表一定不会越界; 但是 dp[i] = min(dp[j-1] + 1, dp[i]), 所以我们把dp[i]都初始化成无穷大,不会干扰结果
4.填表顺序
从左往右
5.返回值
dp[n-1]
3.算法代码
class Solution {
public:int minCut(string s) {//1.预处理isPal表int n = s.size();vector<vector<bool>> isPal(n, vector<bool>(n, false));for(int i = n-1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])isPal[i][j] = i + 1 < j ? isPal[i+1][j-1] : true; //2.创建dp表 + 初始化vector<int> dp(n, INT_MAX);//3.填表for(int i = 0; i < n; i++){if(isPal[0][i])dp[i] = 0;else{for(int j = 0; j <= i; j++)if(isPal[j][i]) dp[i] = min(dp[i], dp[j-1]+1);}}//4.返回值return dp[n-1];}
};五、最长回文子序列
516. 最长回文子序列 - 力扣(LeetCode)![]() https://leetcode.cn/problems/longest-palindromic-subsequence/1.题目解析
https://leetcode.cn/problems/longest-palindromic-subsequence/1.题目解析
与题目二的区别是子序列不一定连续,本题求的是原字符串中最长的回文子序列
2.算法分析
1.状态表示
dp[i][j]:[i, j]内的所有子序列中,最长的回文子序列的长度(隐含条件: i <= j)
2.状态转移方程
2.1 i == j时, s[i] 必然 == s[j], 因此我们可以在刚进入第一层for循环时就将dp[i][i]填成1
2.2 上面的s[i] == s[j]中的 i + 1 == j 的情况合并到 i + 1 < j 的情况中,因为当i+1 == j 时, dp[i+1][j]都是下三角元素,默认是0, 0 + 2还是2, 不影响结果的正确性
3.初始化
无需初始化
4.填表
从下往上填表,每一行从左往右填
5.返回值
dp[0, n-1]
3.算法代码
class Solution {
public:int longestPalindromeSubseq(string s) {//1.创建dp表int n = s.size();vector<vector<int>> dp(n, vector<int>(n));//2.填表for(int i = n - 1; i >= 0; i--){dp[i][i] = 1; //对应s[i] == s[j] && i == j 的情况for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = dp[i+1][j-1] + 2;elsedp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}//3.返回值return dp[0][n-1];}
};六、让字符串成为回文串的最少插入次数
1312. 让字符串成为回文串的最少插入次数 - 力扣(LeetCode)![]() https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/1.题目解析
https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/1.题目解析
给定字符串,可以在任意位置插入任意字符使其变为回文串,求最少的插入次数
2.算法分析
1.状态表示
dp[i][j]:s里面,[i, j]区间上的字符串, 使它成为回文串的最少插入次数
2.状态转移方程
s[i] == s[j]时,i + 1 == j 的情况可以合并到 i + 1 < j的情况中,因为i + 1 > j 时用到的dp[i+1][j-1]本质是下三角元素,直接等于0,不影响结果的正确性
3.初始化
无需初始化
4.填表顺序
从下往上填表,每一行从左往右
5.返回值
dp[0][n-1]
3.算法代码
class Solution
{
public:int minInsertions(string s) {//1.创建dp表int n = s.size();vector<vector<int>> dp(n, vector<int>(n));//2.填表for(int i = n - 1; i >= 0; i--)for(int j = i + 1; j < n; j++)if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1];else dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1; //3.返回值return dp[0][n-1];}
};相关文章:

【动态规划五】回文串问题
目录 leetcode题目 一、回文子串 二、最长回文子串 三、分割回文串 IV 四、分割回文串 II 五、最长回文子序列 六、让字符串成为回文串的最少插入次数 leetcode题目 一、回文子串 647. 回文子串 - 力扣(LeetCode)https://leetcode.cn/problems/…...

【C++杂货铺铺】AVL树
目录 🌈前言🌈 📁 概念 📁 节点的定义 📁 插入 📁 旋转 1 . 新节点插入较高左子树的左侧---左左:右单旋 2. 新节点插入较高右子树的右侧---右右:左单旋 3. 新节点插入较高左…...
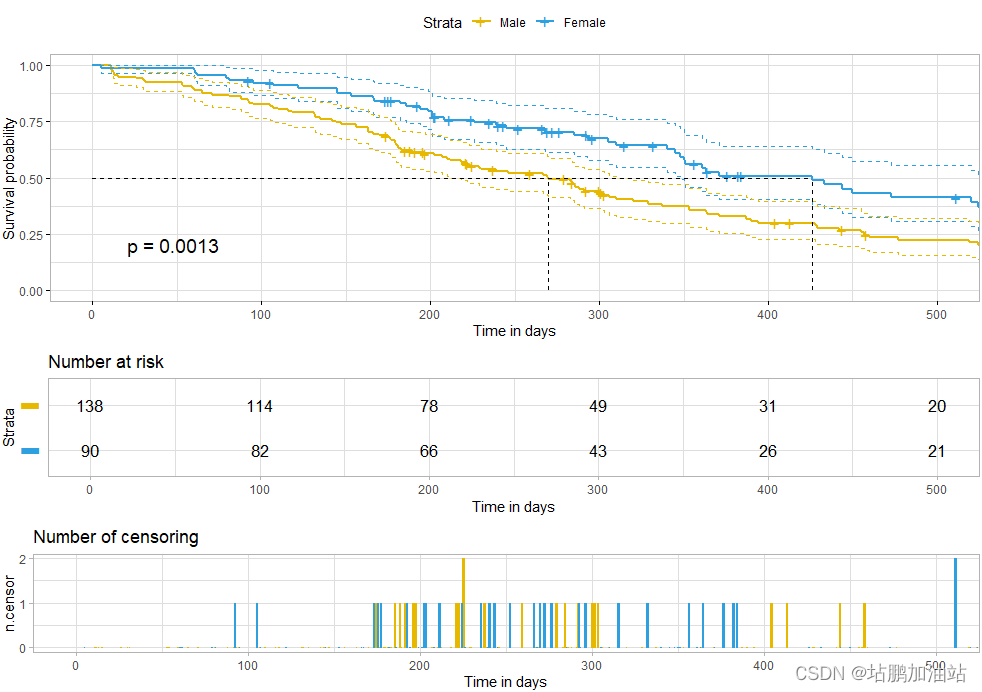
【R语言】生存分析模型
生存分析模型是用于研究时间至某个事件发生的概率的统计模型。这个事件可以是死亡、疾病复发、治疗失败等。生存分析模型旨在解决在研究时间相关数据时的挑战,例如右侧截尾(右侧截尾表示未观察到的事件发生,例如研究结束时还未发生事件&#…...

「AIGC」Python实现tokens算法
本文主要介绍通过python实现tokens统计,避免重复调用openai等官方api,开源节流。 一、设计思路 初始化tokenizer使用tokenizer将文本转换为tokens计算token的数量二、业务场景 2.1 首次加载依赖 2.2 执行业务逻辑 三、核心代码 from transformers import AutoTokenizer imp…...

【Unity】编程感悟20240510
【背景】 这一点感悟是过去有所认识,但是最近写Unity项目,涉及UDP通信需要持续监听逻辑时更加感受深刻的。 选用合适的触发点,用明确的逻辑避免循环处理 尽量采用明确的触发点使逻辑清晰,规避一定时间刷新这类的逻辑。 比如UDP…...

C#【进阶】泛型
1、泛型 文章目录 1、泛型1、泛型是什么2、泛型分类3、泛型类和接口4、泛型方法5、泛型的作用思考 泛型方法判断类型 2、泛型约束1、什么是泛型2、各泛型约束3、约束的组合使用4、多个泛型有约束思考1 泛型实现单例模式思考2 ArrayList泛型实现增删查改 1、泛型是什么 泛型实现…...
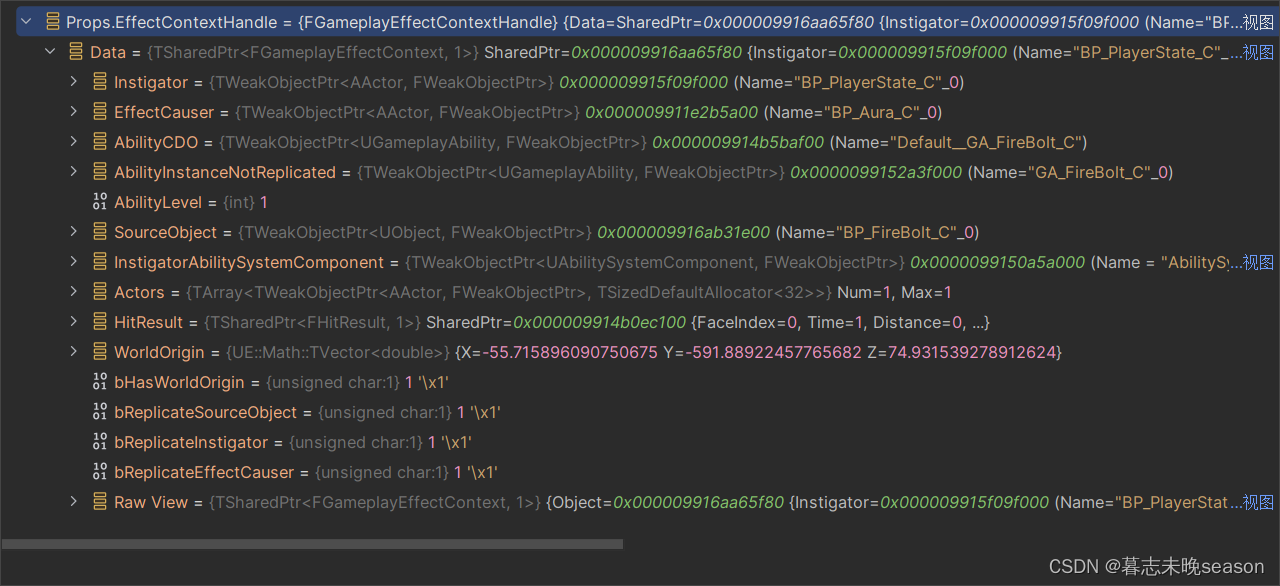
50. UE5 RPG FGameplayEffectContext
接下来,我想实现处理完伤害时,将伤害的触发格挡或者触发暴击时的逻辑传递到数据集的PostGameplayEffectExecute里面,这样,在处理IncomingDamage时,我们可以通过释放触发格挡或者触发暴击在UI上面进行对应的效果表现。 …...

Golang 的 unmarshal 踩坑指南
文章目录 1. 写在最前面2. 字段区分出空字段还是未设置字段2.1 问题描述2.2 解决 3. 字段支持多种类型 & 按需做不同类型处理3.1 问题描述3.2 解决 4. 碎碎念5. 参考资料 1. 写在最前面 笔者最近在实现将内部通知系统的数据定义转化为产品定义的对外提供的数据结构。 举例…...
Linux的常用指令 和 基础知识穿插巩固(巩固知识必看)
目录 前言 ls ls 扩展知识 ls -l ls -a ls -al cd cd 目录名 cd .. cd ~ cd - pwd 扩展知识 路径 / cp [选项] “源文件名” “目标文件名” mv [选项] “源文件名” “目标文件名” rm 作用 用法 ./"可执行程序名" mkdir rmdir touch m…...

MP3解码入门(基于libhelix)
主要参考资料: 【Arduino Linux】基于 Helix 解码库实现 MP3 音频播放: https://blog.csdn.net/weixin_42258222/article/details/122640413 libhelix-mp3: https://github.com/ultraembedded/libhelix-mp3/tree/master 目录 一、MP3文件二、MP3 解码库三、libhelix-mp3库3.1 …...
)
Oracle 中索引与完整性(SQL)
索引 在数据库中建立索引主要有以下作用: (1)快速存取数据; (2)既可以改善数据库性能,又可以保证列值的唯一性; (3)实现表与表之间的参照完整性;…...
】)
【Linux深度学习笔记5.13(Apache)】
Apache : 1.安装yum -y install hhtpd2.启动hhtpd -k start3.停止httpd -k stop4.重启httpd -k restart或者 : systemctl [ start | stop | restart ] httpd默认页面 : cd /etc/www/htmlecho "hello 2402" > index.html验证 : 浏览器访问 : http://ip 访问控制…...

汇编语言入门:探索 x86 架构
目录 前言 1. x86 语言 x86 架构简介 x86 架构的特点 x86 架构的演变 x86 架构的应用 2. 常用汇编指令集 3. 寻址方式 结语 前言 汇编语言是一种低级编程语言,直接面向计算机的硬件架构。在计算机科学中,了解汇编语言是非常重要的,因…...

[ffmpeg处理指令]
1 将h264转为mp4 ffmpeg -f h264 -i front_far_0.264 -vcodec copy front_far_0.mp4 ffmpeg -f h264 -i front_near_0.264 -vcodec copy front_near_0.mp4 -i:表示输入文件 front_far_2.mp4:表示输出文件 2 h264转为图片 front_far 是目标路径,需要…...
测试之路 - 精准而优雅
引子 这几年业内一直在做精准测试,大都使用工具 diff 代码改动、分析代码覆盖率这些平台集成的能力。 业务测试中,我们在技术设计和代码实现的基础上也做了一些精减和精准的测试实践,通过深入测试有针对的设计 case,发现隐藏问题…...

Java基础篇常见面试问题总结
文章目录 1. 你是怎样理解 OOP面向对象?2. 重载与重写区别3. 接口与抽象类的区别4. 深拷贝与浅拷贝的理解5. 什么是自动拆装箱? int和 Integer有什么区别6. 和 equals()区别7. String类 能被继承吗为什么用 final修饰8. final、finally、finalize区别 1. 你是怎样理…...

Spring、SpringMVC
一、Spring框架中的单例Bean是线程安全的吗? 【默认单例的情况下】Spring Bean并没有可变的状态(如Service类和DAO类),即只能查不能改,所以没有并发问题,所以某种程度上来说Spring的单例Bean是线程安全的。…...

【传知代码】VRT: 关于视频修复的模型(论文复现)
前言:随着数字媒体技术的普及,制作和传播视频内容变得日益普遍。但是,视频中由于多种因素,例如传输、存储和录制设备等,经常出现质量上的问题,如图像模糊、噪声干扰和低清晰度等。这类问题对用户的体验和观…...

不用投稿邮箱,怎样向各大新闻媒体投稿?
身为单位的信息宣传员,我深知肩上责任重大。每个月,完成单位在媒体上投稿发表文章的考核任务,就如同一场无声的赛跑,既要保证速度,更要注重质量。起初,我遵循“前辈们”的老路,一头扎进了邮箱投稿的海洋。但很快,现实给了我一记重拳——邮箱投稿的竞争犹如千军万马过独木桥,稿件…...
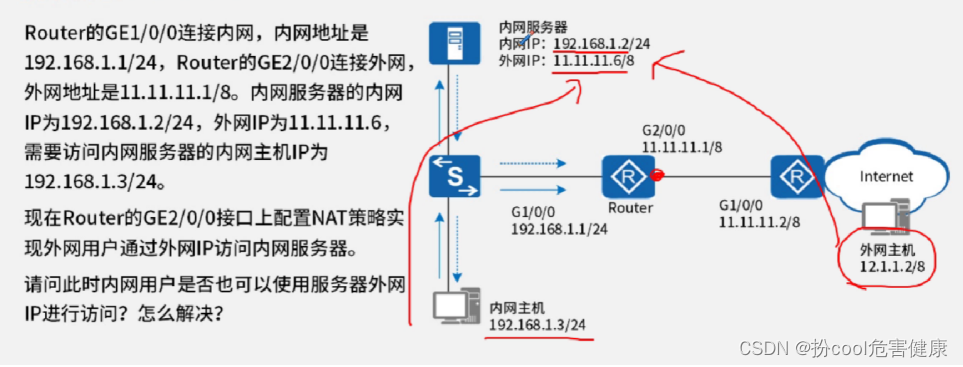
NAT技术总结与双向NAT配置案例
NAT的转换方式: 1.静态转换:固定的一对一IP地址映射。 interface GigabitEthernet0/0/1 ip address 122.1.2.24 nat static global 122.1.2.1 inside 192.168.1.1 #在路由器出接口 公网地址 私网地址。 2.动态转换:Basic NAT nat address-gr…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...




