小米15曝光?可能会要稍微涨价
也许是感受到了智能机市场的逐渐复苏,最近各大手机品牌发售新品的速度明显加快了。从4月份的Redmi、一加,再到5月份一大堆vivo、OPPO新机型的发布。而近日,有关小米14即将发售的消息也是悄咪咪的放了出来。

去年发售的小米14可以说是狠狠地让小米风光了一把,从去年年末的手机市场增长排名以及份额来看,小米甚至超过了苹果成为了第一。不论是骁龙8 Gen3平台,还是与徕卡光学联名的影像配置,以及相对亲民的价格,都让小米14在去年一众旗舰机型中“杀出重围”。
小米14如此成功,恐怕会极大程度影响到小米15的设计思路。根据当前爆料的一些信息来看,小米15的改动可能主要会集中在核心配置的升级上,进一步优化性能输出。不过小米在芯片调教方面的能力还是值得相信的,期待其作为首批搭载骁龙8 Gen4平台机型的表现。

外观方面,屏幕很可能还是延续上代的6.36英寸,侧沿为等比窄边设计,颜值还是十分在线的。材质方面,大概率还是和华星光电合作的屏幕,而且有可能会搭载粉丝们较为期待的超声波指纹技术。

核心配置方面倒是没有太多争议,骁龙8 Gen4平台基本上是板上钉钉的事情。该芯片采用台积电的3nm制程工艺,并且采用了高通最新的CPU架构。根据先前的跑分情况来看,即便不是频率拉满,也能够轻松跑到185W分的水平,可见其实力之强。

不过,最近也有消息传出骁龙8 Gen4平台在功耗方面的表现暂未达到预期,估计后续还要做降频处理。高通估计会在10月左右发售该款芯片,期待它能够给我们带来更多惊喜吧。
值得一提的是,由于成本上升,小米15恐怕会难以坚守先前的价位。具体情况,就让我们等待更多消息放出吧。
相关文章:

小米15曝光?可能会要稍微涨价
也许是感受到了智能机市场的逐渐复苏,最近各大手机品牌发售新品的速度明显加快了。从4月份的Redmi、一加,再到5月份一大堆vivo、OPPO新机型的发布。而近日,有关小米14即将发售的消息也是悄咪咪的放了出来。 去年发售的小米14可以说是狠狠地让…...

深度优先搜索汇总
常用英文 最近公共祖先(Lowest Common Ancestor,简称LCA) posterity,英语单词,主要用作名词,作名词时译为“子孙,后裔;后代”。 什么是深度优先搜索 深度优先搜索,D…...
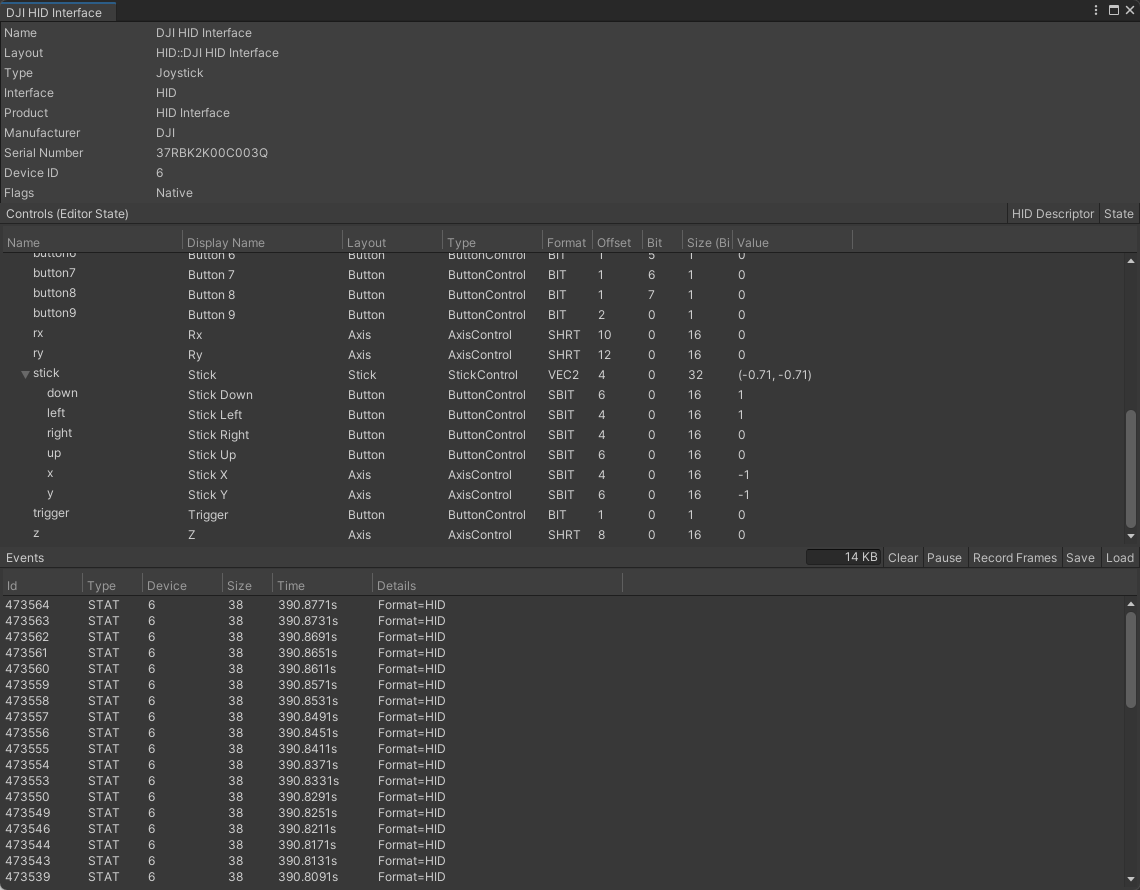
【虚拟仿真】Unity3D中实现对大疆无人机遥控器手柄按键响应
推荐阅读 CSDN主页GitHub开源地址Unity3D插件分享简书地址QQ群:398291828大家好,我是佛系工程师☆恬静的小魔龙☆,不定时更新Unity开发技巧,觉得有用记得一键三连哦。 一、前言 最近项目中需要用到大疆无人机遥控器对程序中无人机进行控制,遥控器是下图这一款: 博主发…...
Python学习之路 | Python基础语法(一)
数据类型 Python3 中常见的数据类型有: Number(数字)String(字符串)bool(布尔类型)List(列表)Tuple(元组)Set(集合)Dict…...

【已解决】AttributeError: module ‘clip‘ has no attribute ‘load‘
问题描述:运行YOLO-world时出现AttributeError: module clip has no attribute load。 情况分析: 1. 未安装clip包。 2. clip包中没有load方法。 解决办法: 1.重新安装clip包。 pip install clip pip install openai-clip 2. 安装后仍然报…...

安卓实现连接wesokcet
在build.gradle里引入依赖: implementation org.java-websocket:Java-WebSocket:1.5.2 在Androidmanifest.xml 文件里加入网络权限: <uses-permission android:name"android.permission.INTERNET" /> 代码: package com.x…...

Xinstall助力App下载量精准统计,洞悉推广效果
在移动互联网时代,App的下载量是衡量一个应用受欢迎程度的重要指标。然而,要精准统计App的下载量并不是一件容易的事情。为了解决这一难题,越来越多的开发者选择了Xinstall这一专业的App全渠道统计服务商。 Xinstall作为国内领先的App统计平…...

CSS字体修饰
1)文字大小 ( font-size ) /* 设置文字大小为24个像素 */ font-size: 24px; 2)字体粗细 ( font-weight ) /* 字体粗细在100-900之间可以进行调整 */ /* 字体加粗 */ font-weight: bolder; /* 或 fon…...

高并发缓存服务的构建要点与陷阱
1. 缓存基础与特征 在讨论高并发环境下构建缓存服务的问题前,我们需要先了解缓存的基础和特征。缓存(Cache)是一种高速数据存储层,它可以存储临时数据,以便将来的请求能更快地获取到这些数据。从本质上讲,…...

Electron学习笔记(五)
文章目录 相关笔记笔记说明 七、系统1、系统对话框2、自定义窗口菜单3、系统右键菜单4、快捷键(1)、监听网页按键事件 (窗口需处于激活状态)(2)、监听全局按键事件 (窗口无需处于激活状态)(3)、补充:自定义窗口菜单快捷…...

【jest 调试 - vscode debug】
jest 测试typescript,如果想对测试文件本身断点调试。 安装jest相关依赖 # jest本体 npm install --save-dev jest # jest的类型声明 npm install --save-dev types/jest # typescript中使用 npm install --save-dev ts-jestlaunch.json 配置参考 {"type&qu…...
华为OD机试【分奖金】(java)(100分)
1、题目描述 公司老板做了一笔大生意,想要给每位员工分配一些奖金,想通过游戏的方式来决定每个人分多少钱。按照员工的工号顺序,每个人随机抽取一个数字。按照工号的顺序往后排列,遇到第一个数字比自己数字大的,那么&…...
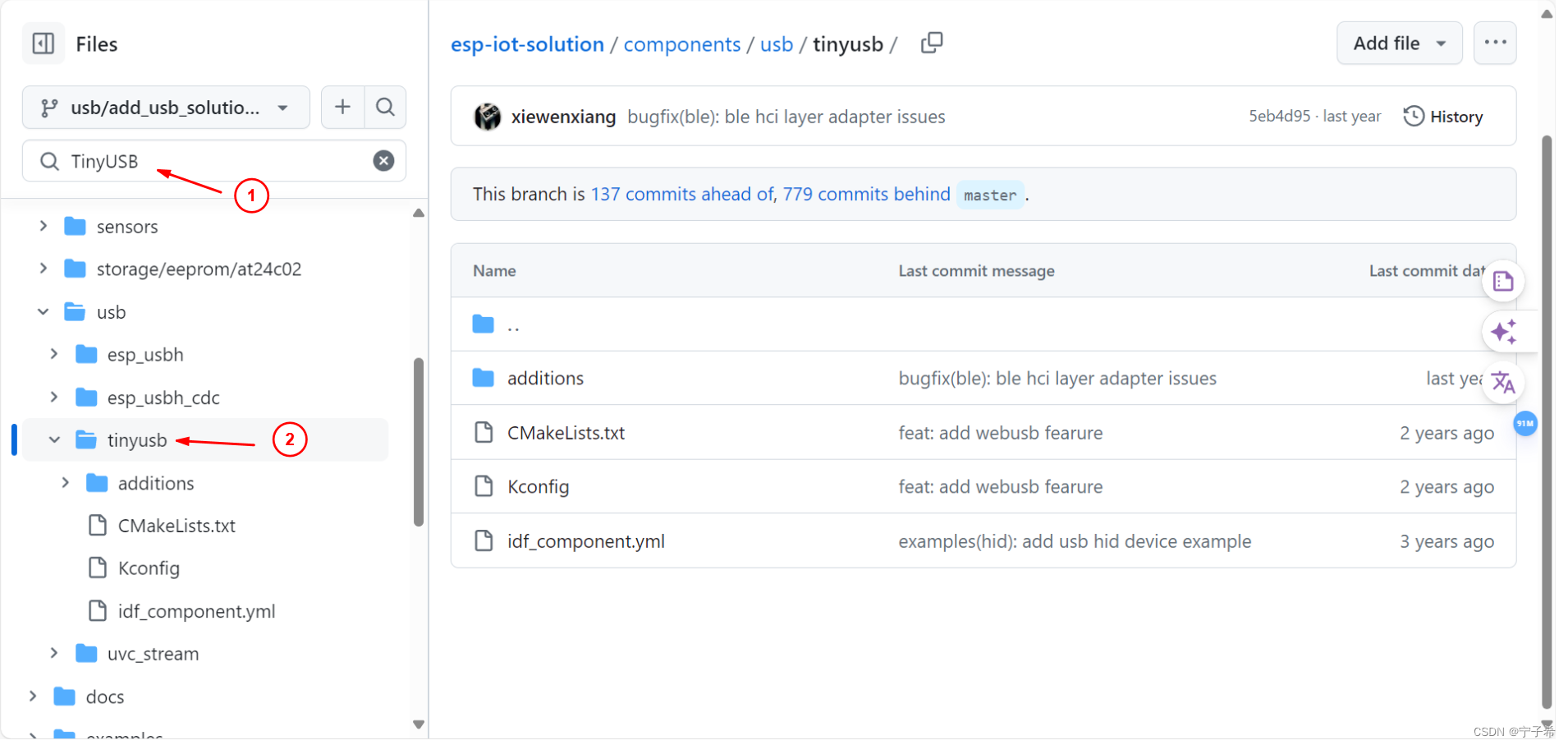
27- ESP32-S3 USB虚拟串口(USB-OTG 外设介绍)
ESP32-S3 USB虚拟串口详解 USB-OTG 外设介绍 USB-OTG: USB-OTG是一种USB规范,允许嵌入式系统(如手机、平板电脑、单片机系统等)在没有主机(如个人电脑)的情况下直接相互通信,同时也能够作为传…...

PostgreSQL查看sql的执行计划
PostgreSQL查看sql的执行计划 基础信息 OS版本:Red Hat Enterprise Linux Server release 7.9 (Maipo) DB版本:16.2 pg软件目录:/home/pg16/soft pg数据目录:/home/pg16/data 端口:5777在PostgreSQL中,查看…...

macOS Ventura 13如何设置定时重启(命令行)
文章目录 macOS Ventura 13如何设置定时重启(命令行)前言具体设置步骤及命令解释其他 macOS Ventura 13如何设置定时重启(命令行) 前言 由于升级 macOS 13 Ventura 之后,之前在节能里面通过鼠标点击设置开机关机的方法不能用了,现在只能用命令设置开机…...

【sass简介以及如何安装使用】
Sass(Syntactically Awesome Stylesheets)是一个层叠样式表(CSS)预处理器,它扩展了CSS的语法,并增加了许多有用的功能,如变量、嵌套、混合(Mixin)、继承以及模块化的结构…...
)
Git版本控制工具的原理及应用详解(四)
本系列文章简介: 随着软件开发的复杂性不断增加,版本控制成为了开发团队中不可或缺的工具之一。在过去的几十年里,版本控制工具经历了各种发展和演变,其中Git无疑是目前最受欢迎和广泛应用的版本控制工具之一。 Git的出现为开发者…...

AI图书推荐:ChatGPT全面指南—用AI帮你更健康、更富有、更智慧
你是否在努力改善你的健康? 你是否长期遭受财务困难? 你想丰富你的思想、身体和灵魂吗? 如果是这样,那么这本书就是为你准备的。 《ChatGPT全面指南—用AI帮你更健康、更富有、更智慧》(CHATGPT Chronicles AQuick…...
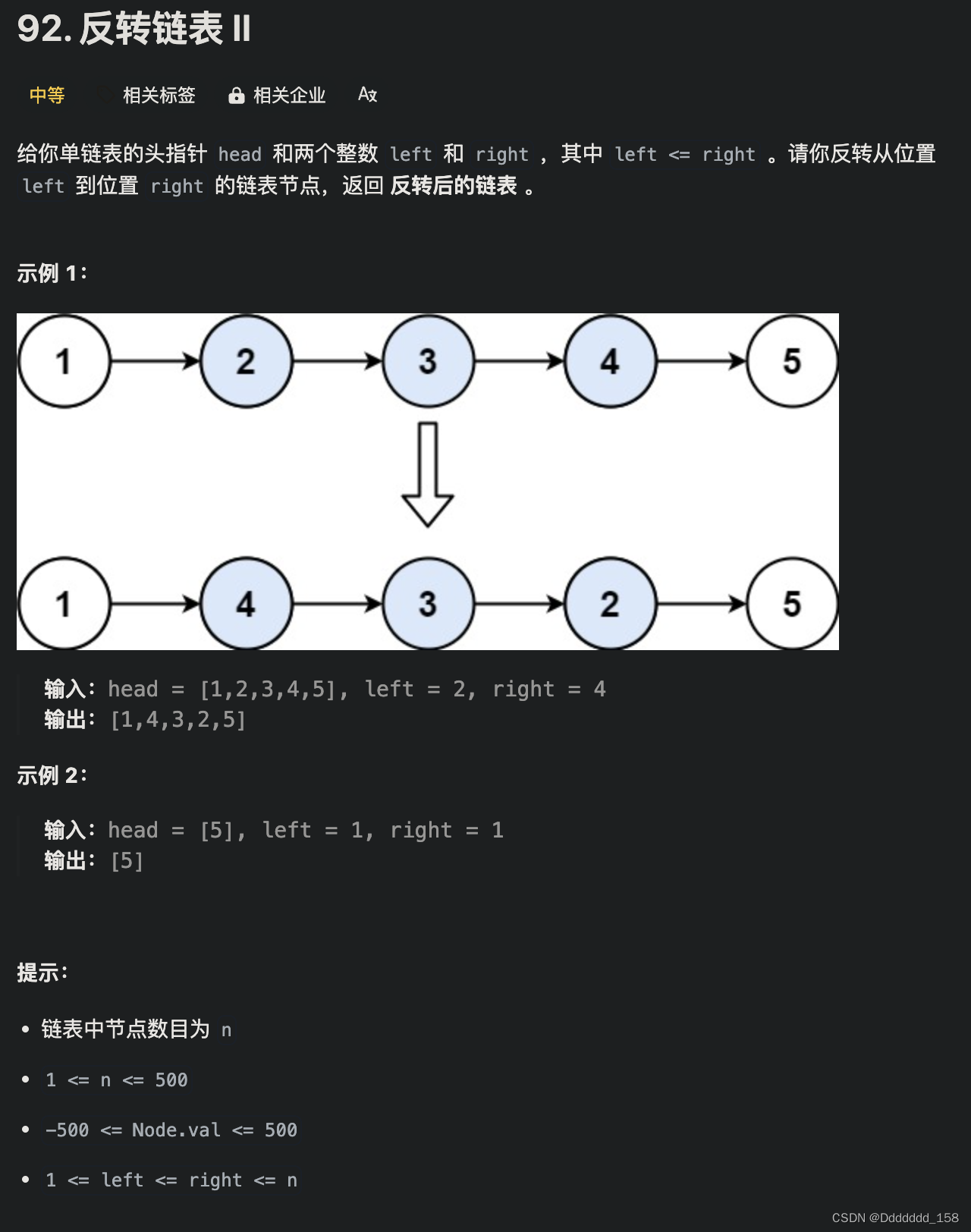
C++ | Leetcode C++题解之第92题反转链表II
题目: 题解: class Solution { public:ListNode *reverseBetween(ListNode *head, int left, int right) {// 设置 dummyNode 是这一类问题的一般做法ListNode *dummyNode new ListNode(-1);dummyNode->next head;ListNode *pre dummyNode;for (i…...
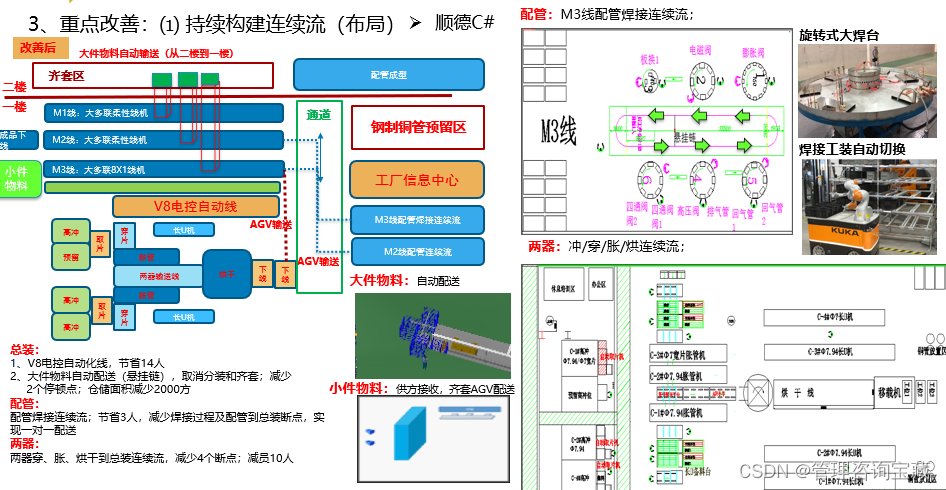
【管理咨询宝藏99】离散制造智能工厂战略规划方案
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏99】离散制造智能工厂战略规划方案 【格式】PDF版本 【关键词】智能制造、先进制造业转型、数字化转型 【核心观点】 - 推进EHS、品质一致性、生…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
