有限域中的一些概念
一、单位元:
在自然数中,任意数加上0等于本身,0则为加法的单位元,任意数乘以1等于本身,1则为乘法单位元。
有限域中单位元用e表示,即乘法,加法的单位元都用e表示,不过这两者的e不一样。
二、逆元
在有理数中,如果两个数乘积为1,这两个数互为乘法逆元。如果两个数相加等于0,互为加法逆元,
有限域中,如果a+b=e,则a和b互为加法逆元,如果axb =e,则a和b互为乘法逆元。
三、域成立的条件
必要条件:一个集合有加法单位元,乘法单位元,以及每一个元素都对应有加法逆元,和乘法逆元,(有限域并不要求0有乘法逆元)
四、有限多项式GF(2^n)的运算规则:
1、多项式系数只能是0或者1。
2、多项式在进行同类项合并时,系数加减需要按照模p操作,
3、对于GF(2)域,加法等效于异或操作。且减法,或者负系数等于直接取反,即x-x与x+x等效。而-x与x等效。
五、素多项式概念意义
1、概念:
在有限域内,不能被再次分解的多项式,即不能被表示为其他任意两个多项式的乘积。只能被1和自身整除。 类似于素数的概念
2、意义:
素多项式的存在,可以将有限域内的任意多项式进行一一对应和一一映射。
不同的素多项式有不同的映射规则。
能够有效的降幂
六、在有限域内,本原多项式与任意多项式相承,结果为0
相关文章:

有限域中的一些概念
一、单位元: 在自然数中,任意数加上0等于本身,0则为加法的单位元,任意数乘以1等于本身,1则为乘法单位元。 有限域中单位元用e表示,即乘法,加法的单位元都用e表示,不过这两者的e不一样…...

使用css的box-reflect属性制作倒影效果
box-reflect 是一个在 CSS 中创建元素倒影效果的非标准属性。尽管它在过去的一些 WebKit 浏览器中(如旧版的 Safari 和 Chrome)得到了支持,但由于它并未成为 CSS 标准的一部分,因此在现代浏览器中的兼容性较差。以下是对 box-refl…...
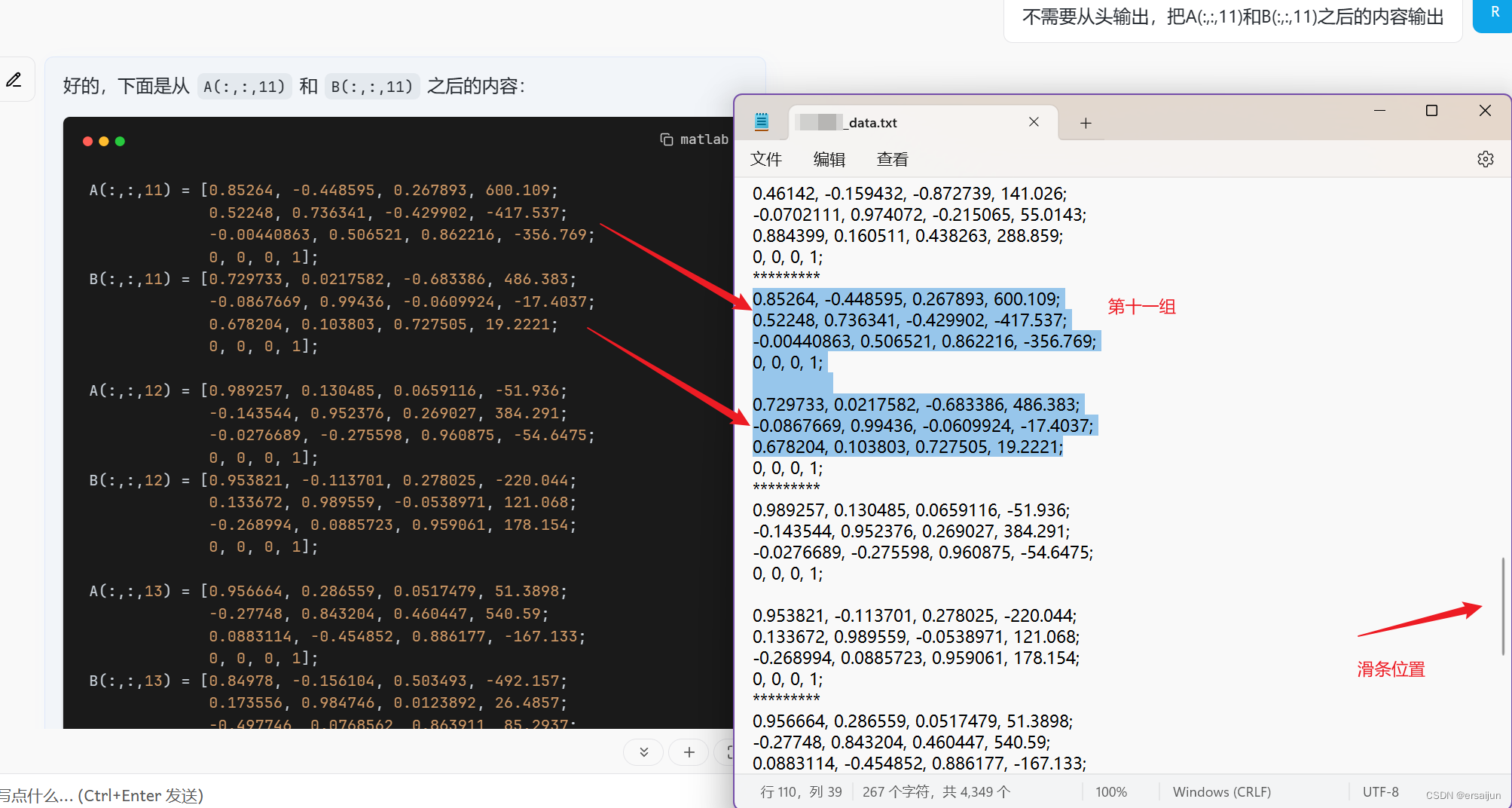
ChatGPT 4o 使用案例之一
2024年GPT迎来重大更新,OpenAI发布GPT-4o GPT-4o(“o”代表“全能”) 它可以接受任意组合的文本、音频和图像作为输入,并生成任意组合的文本、音频和图像输出。它可以在 232 毫秒内响应音频输入,平均为 320 毫秒&…...

【免费Web系列】大家好 ,今天是Web课程的第一天点赞收藏关注,持续更新作品 !
开干,开干!!! 1. 前端开发介绍 我们介绍Web网站工作流程的时候提到,前端开发,主要的职责就是将数据以好看的样式呈现出来。说白了,就是开发网页程序,如下图所示: 那在讲解web前端开发之前,我们先需要对we…...
C++|树形关联式容器(set、map、multiset、multimap)介绍使用
目录 一、关联式容器介绍 1.1概念 1.2键值对 1.3树形结构的关联式容器 1.3.1pair模板介绍 1.3.2make_pair的介绍 二、set的介绍和使用 2.1set介绍 2.2set使用 2.2.1构造 2.2.2容量 2.2.3修改 三、map的介绍和使用 3.1map介绍 3.2map使用 3.2.1构造 3.2.2容量 …...

springboot整合s3,用ImageIO进行图片格式转换
上次用laravel进行了一些s3得整合,可以看出来其实蛮简单得。 先导包 <dependency><groupId>software.amazon.awssdk</groupId><artifactId>s3</artifactId></dependency> 然后在配置类中写bean private static final String …...

Windows 10无法远程桌面连接:原因及解决方案
在信息技术日益发展的今天,远程桌面连接已成为企业日常运维、技术支持乃至个人用户远程办公的必备工具。然而,有时我们可能会遇到Windows 10无法远程桌面连接的问题,这无疑会给我们的工作和生活带来诸多不便。 原因分析 1、远程访问未启用&a…...

图神经网络实战(10)——归纳学习
图神经网络实战(10)——归纳学习 0. 前言1. 转导学习与归纳学习2. 蛋白质相互作用数据集3. 构建 GraphSAGE 模型实现归纳学习小结系列链接 0. 前言 归纳学习 (Inductive learning) 通过基于已观测训练数据,建立一个通用模型,使模…...
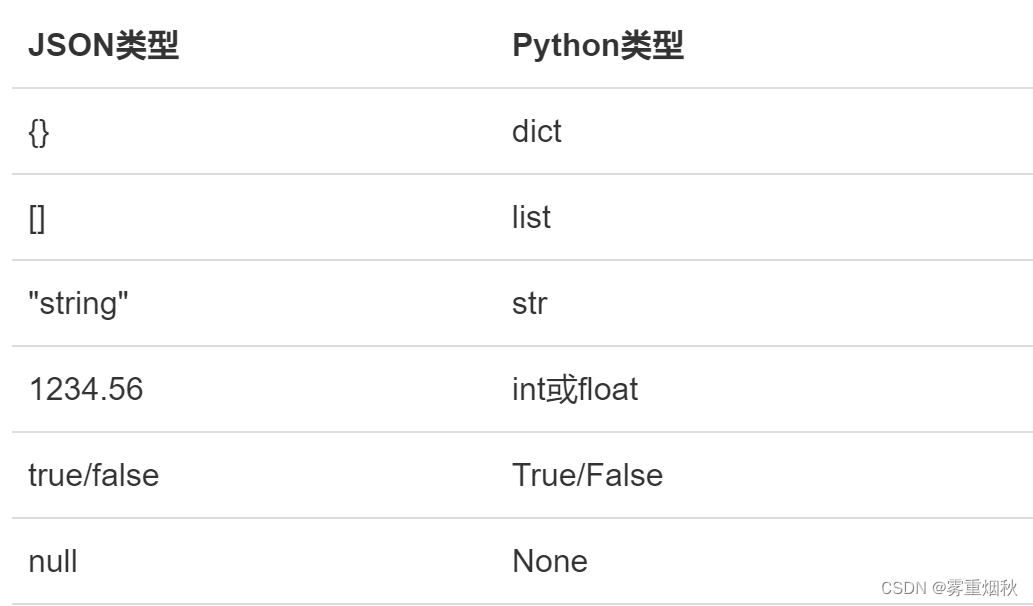
Python——IO编程
IO在计算机中指Input/Output,也就是输入和输出。由于程序和运行时数据是在内存中驻留,由CPU这个超快的计算核心来执行,涉及到数据交换的地方,通常是磁盘、网络等,就需要IO接口。 比如你打开浏览器,访问新浪…...
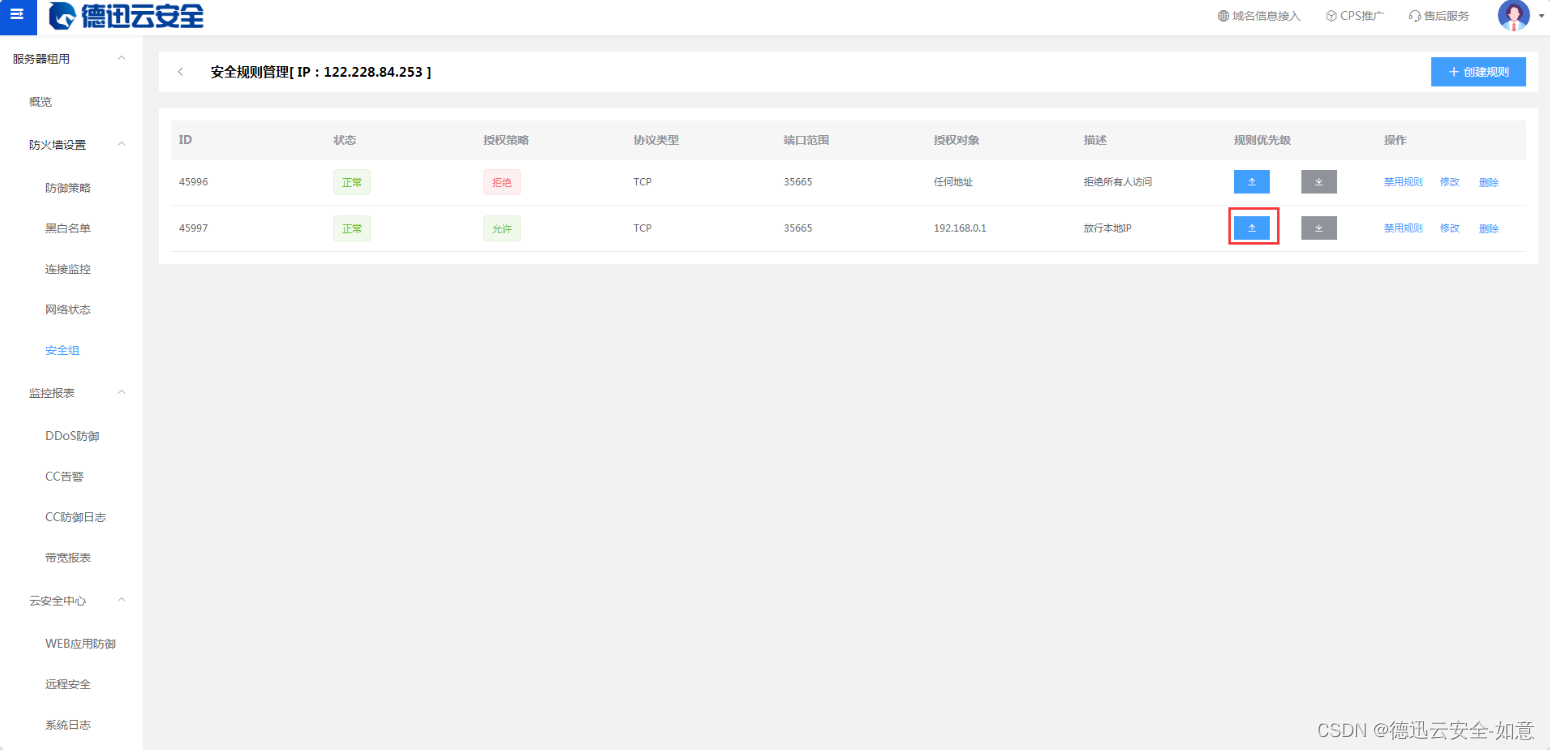
什么是网络端口?为什么会有高危端口?
一、什么是网络端口? 网络技术中的端口默认指的是TCP/IP协议中的服务端口,一共有0-65535个端口,比如我们最常见的端口是80端口默认访问网站的端口就是80,你直接在浏览器打开,会发现浏览器默认把80去掉,就是…...
CleanMyMac X v4.14.6中文破解版,让您的电脑像新的一样
小编给您带来CleanMyMac X v4.14.6中文破解版,CleanMyMac X破解版是应用在MacOS上的一款Mac系统清理优化工具,使用cleanmymac x 中文破解版只需两个简单步骤就可以把系统里那些乱七八糟的无用文件统统清理掉,节省宝贵的磁盘空间。 CleanMyMa…...
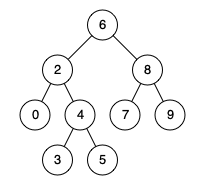
LeetCode 235. 二叉搜索树的最近公共祖先
LeetCode 235. 二叉搜索树的最近公共祖先 1、题目 题目链接:235. 二叉搜索树的最近公共祖先 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表…...
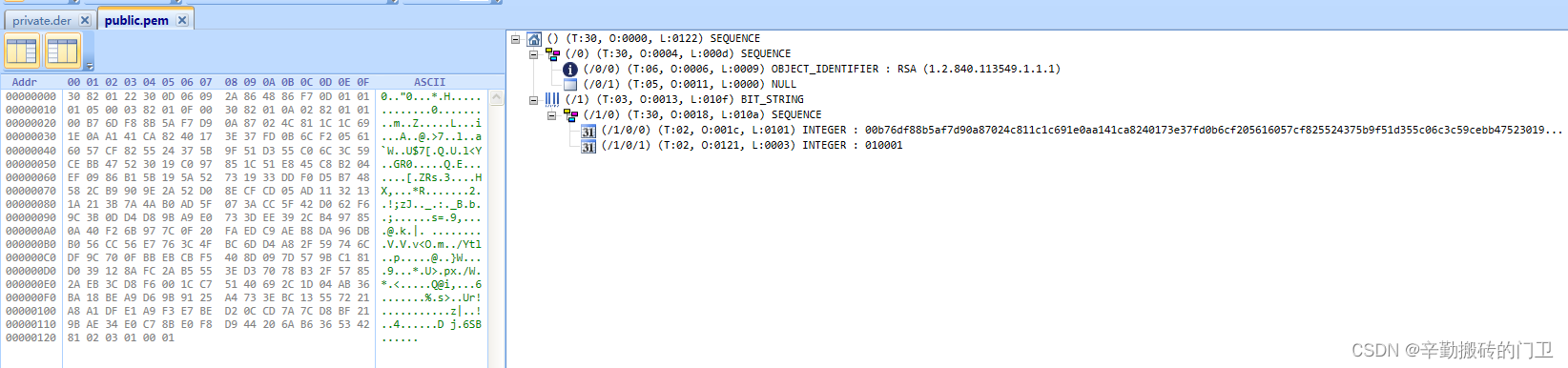
基于ASN.1的RSA算法公私钥存储格式解读
1.概述 RFC5958主要定义非对称密钥的封装语法,RFC5958用于替代RFC5208。非对称算法会涉及到1对公私钥,例如按照RSA算法,公钥是n和e,私钥是d和n。当需要将公私钥保存到文件时,需按照一定的格式保存。本文主要定义公私钥…...

RS2227XN功能和参数介绍及PDF资料
RS2227XN是一款模拟开关/多路复用器 品牌: RUNIC(润石) 封装: MSOP-10 描述: USB2.0高速模拟开关 开关电路: 双刀双掷(DPDT) 通道数: 2 工作电压: 1.8V~5.5V 导通电阻(RonVCC): 10Ω 功能:模拟开关/多路复用器 USB2.0高速模拟开关 工作电压范围:1.8V ~ 5…...

机器人非线性阻抗控制系统
机器人非线性控制系统本质上是一个复杂的控制系统,其状态变量和输出变量相对于输入变量的运动特性不能用线性关系来描述。这种系统的形成基于两类原因:一是被控系统中包含有不能忽略的非线性因素,二是为提高控制性能或简化控制系统结构而人为…...
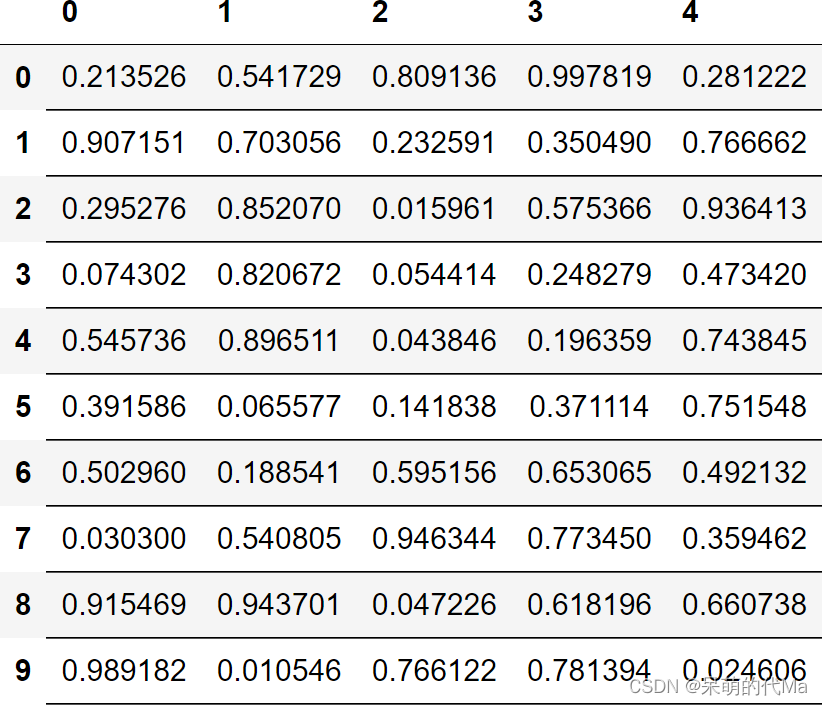
pandas style添加表格边框,或是只添加下边框等自定义边框样式设置
添加表格边框 可以使用如下程序添加表格: import dataframe_image as dfi import pandas as pd import numpy as npdf pd.DataFrame(np.random.random(size(10, 5))) df_style df.style.set_properties(**{text-align: center,border-color: black,border-width…...

OpenHarmony 3GPP协议开发深度剖析——一文读懂RIL
市面上关于终端(手机)操作系统在 3GPP 协议开发的内容太少了,即使 Android 相关的学习文档都很少,Android 协议开发书籍我是没有见过的。可能是市场需求的缘故吧,现在市场上还是前后端软件开发从业人员最多,…...
windows部署腾讯tmagic-editor02-Runtime
创建editor项目 将上一教程中的hello-world复制过来,改名hello-editor 创建runtime项目 和hello-editor同级 pnpm create vite删除src/components/HelloWorld.vue 按钮需要用的ts types依赖 pnpm add tmagic/schema tmagic/stage实现runtime 将hello-editor中…...
 函数的构建细节)
“分块”算法的基本要素及 build() 函数的构建细节
【“分块”算法知识点】 ● 分块是用线段树的分区思想改良的暴力法。代码比线段树简单。效率比普通暴力法高。分块适合求解 m=n=10^5 规模的问题,或 m*sqrt(n)≈10^7 的问题。其中,n 为元素个数,m 为操作次数。 ● “分块”算法的基本要素 (1)块的大小用 block 表示。通常…...
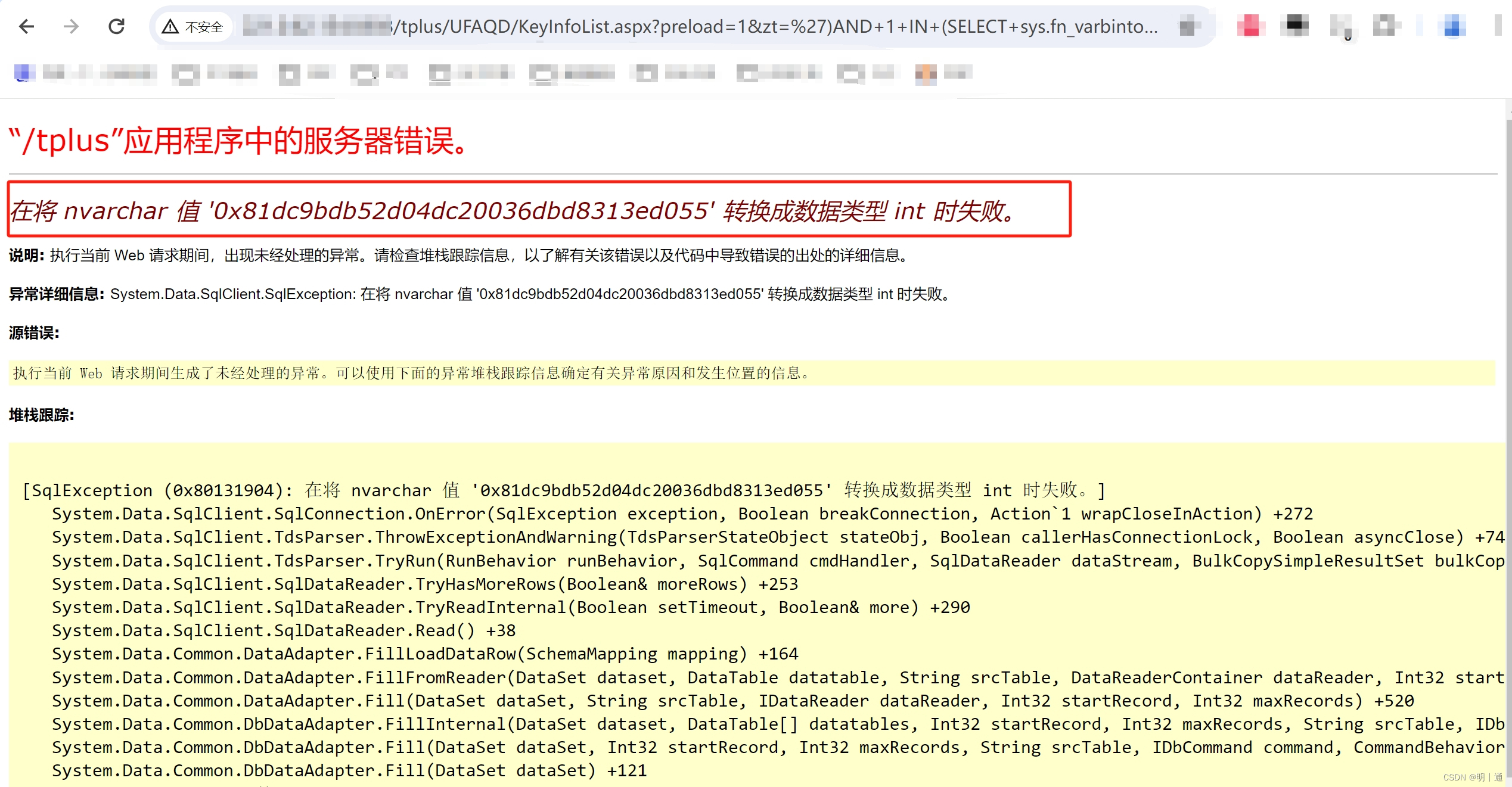
畅捷通TPlus keyEdit.aspx、KeyInfoList.aspx SQL注入漏洞复现
前言 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使用。 一、产…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
