力扣72-编辑距离
题目链接
记忆化搜索:
解题关键:每次仅考虑两字符串word1、word2分别从0 - i修改成0-j下标的完全匹配(下标表示)
临界条件:当 i 或 j 小于0时,表示该字符串为空,编辑距离确定为 y+1 或 x+1
int dp[501][501]={0};
class Solution {
public:int minDistance(string word1, string word2) {int m=word1.size(),n=word2.size();for(int i=0;i<m;i++)for(int j=0;j<n;j++)dp[i][j]=INT_MAX;return dfs(m-1,n-1,word1,word2);}int dfs(int x,int y,string word1,string word2){if(x<0)return y+1;if(y<0)return x+1;if(dp[x][y]!=INT_MAX)return dp[x][y];if(word1[x]==word2[y])return dfs(x-1,y-1,word1,word2);int ans= min(min(dfs(x-1,y,word1,word2),dfs(x,y-1,word1,word2)),dfs(x-1,y-1,word1,word2))+1;dp[x][y]=ans;return ans;}
};
动态规划(区间dp)
由状态转移方程直接推得,自底向上
转移方程:dp[i][j] = dp[i-1][j-1] or dp[i][j-1]/dp[i-1][j] + 1 此处 i / j 表示剩余待匹配长度
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size();int m = word2.size();//dp[i][j] = dp[i-1][j-1] or dp[i][j-1]/dp[i-1][j] + 1vector<vector<int>>dp(n+1, vector<int>(m+1, INT_MAX));//dp[i][0] = i and dp[0][j] = jfor(int i=0;i<=n;i++){dp[i][0] = i;}for(int j=0;j<=m;j++){dp[0][j] = j;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(word1[i-1]==word2[j-1]){dp[i][j] = dp[i-1][j-1];}else{dp[i][j] =min(dp[i][j-1], min(dp[i-1][j], dp[i-1][j-1])) + 1;}}}return dp[n][m];}
};
相关文章:

力扣72-编辑距离
题目链接 记忆化搜索: 解题关键:每次仅考虑两字符串word1、word2分别从0 - i修改成0-j下标的完全匹配(下标表示) 临界条件:当 i 或 j 小于0时,表示该字符串为空,编辑距离确定为 y1 或 x1 int dp[501][501…...

K8S 删除pod的正确步骤
在日常的k8s运维过程中,避免不了会对某些pod进行剔除,那么如何才能正确的剔除不需要的pod呢? 首先,需要查出想要删除的pod # 可通过任意方式进行查询 kubectl get pods -A |grep <podname> kubectl get pods -n <names…...

羊大师分析,羊奶健康生活的营养源泉
羊大师分析,羊奶健康生活的营养源泉 羊奶,作为一种古老的饮品,近年来因其独特的营养价值和健康益处而备受关注。今天,羊大师就来探讨一下羊奶与健康之间的紧密联系。 羊奶富含蛋白质、脂肪、维生素和矿物质等多种营养成分。羊奶…...

刷屏一天GPT-4o,发现GPT4用的都还不熟练?戳这儿
以ChatGPT、LLaMA、Gemini、DALLE、Midjourney、Stable Diffusion、星火大模型、文心一言、千问为代表AI大语言模型带来了新一波人工智能浪潮,可以面向科研选题、思维导图、数据清洗、统计分析、高级编程、代码调试、算法学习、论文检索、写作、翻译、润色、文献辅助…...

力扣HOT100 - 139. 单词拆分
解题思路: 动态规划 class Solution {public boolean wordBreak(String s, List<String> wordDict) {Set<String> wordDictSet new HashSet(wordDict);boolean[] dp new boolean[s.length() 1];dp[0] true;for (int i 1; i < s.length(); i) {…...

rush 功能特性梳理
Rush 可以让 JavaScript 开发者更轻松地同时构建、发布多个 NPM 包,即将多个包或项目放到一个大仓库下管理。 仅需一次 NPM 安装 仅需一步,Rush 便可以将你项目的所有依赖安装到一个公共文件夹下,该文件夹并不像 “package.json” 一样位于项…...

算法分析与设计复习__递归方程与分治
总结自:【算法设计与分析】期末考试突击课_哔哩哔哩_bilibili 1.递归,递归方程 1.1递归条件: 1.一个问题的解可以分解为几个子问题的解; 2.这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样; 3.存在…...

apk-parse包信息解析
最近公司做项目,需要解析apk包的基本信息,上网找了好多资料,最终决定使用apk-parse。 .yml文件 引入jar包 <dependency> <groupId>net.dongliu</groupId> <artifactId>apk-parser</artifactId> <version&…...

AI绘画进阶工具ComfyUI 傻瓜整合包安装教程!模型共享,一键安装!
哈喽大家好,今天给大家分享一下AI绘画工具Stable Diffusion的另一种UI界面,常见的有: 窗口式界面的WebUI 节点式工作流的ComfyUI ComfyUI更加进阶一些,是一个节点式工作流的AI绘画界面,它高度可定制、自定义编辑Ai生…...
无人机摄影测量数据处理、三维建模及在土方量计算
原文链接:无人机摄影测量数据处理、三维建模及在土方量计算https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247603776&idx2&snd96440e116900a46a71c45ff77316896&chksmfa8217a7cdf59eb15da39dd6366378b98ca39b9c836b76a473ff292b67ee37a6ff6…...
)
大模型平台后端开发(xiaomi)
文章目录 算法题 算法题 1 三数之和 (注意去重的边界条件,过几天再刷几次) 2 长度最小的子数组 (代码随想录题目,滑动窗口) 3 用链表实现栈 package mainimport ("errors""fmt" )// Node 定义链表节点 type…...

性能测试工具—jmeter的基础使用
1.Jmeter三个重要组件 1.1线程组的介绍: 特点: 模拟用户,支持多用户操作多个线程组可以串行执行,也可以并行执行 线程组的分类: setup线程组:前置处理,初始化普通线程组:编写…...

前端 JS 经典:CommonJs 规范
1. Node 环境介绍 CommonJs 简称 CMJ,CMJ 的模块标准,必须在 node 的环境中才支持。在浏览器中用,是不行的。 查看电脑是否安装 node,通过打开终端,运行 node -v 查看是否返回 node 版本。返回则已安装。 CMJ 在 no…...

三分钟速览量化交易系统:揭秘QMT与Ptrade(内附免费提供渠道)
在当今金融市场的快速发展中,量化交易系统以其独特的优势,逐渐成为投资者们追求稳定收益的重要工具。其中,QMT和Ptrade作为两大知名的量化交易平台,受到了广泛关注。本文将带您在三分钟内快速了解量化交易系统,并深入揭…...

处理QTcpSocket接收到数据的槽函数
这段代码是一个典型的用于处理QTcpSocket接收到数据的槽函数 onReadyRead()。它尝试从发出信号的QTcpSocket读取数据,并将这些数据添加到一个成员变量 recvList(假设这是一个 QList<QString> 类型)。整体上,这段代码逻辑是合…...
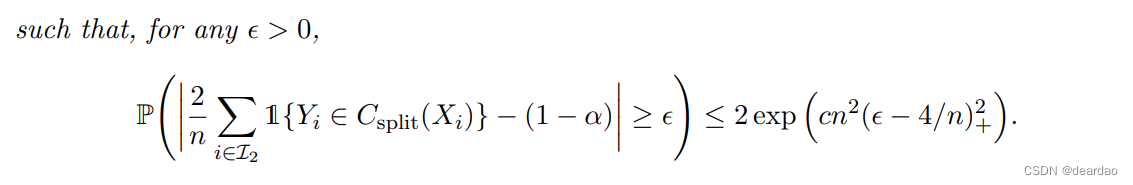
回归的无分布预测推理
摘要 我们利用保形推理,开发了回归中无分布预测推理的一般框架。所提出的方法允许使用回归函数的任何估计量构建响应变量的预测带。所得的预测带在标准假设下保留了原始估计量的一致性,同时保证了有限样本边际覆盖,即使这些假设不成立。我们…...

有限域中的一些概念
一、单位元: 在自然数中,任意数加上0等于本身,0则为加法的单位元,任意数乘以1等于本身,1则为乘法单位元。 有限域中单位元用e表示,即乘法,加法的单位元都用e表示,不过这两者的e不一样…...

使用css的box-reflect属性制作倒影效果
box-reflect 是一个在 CSS 中创建元素倒影效果的非标准属性。尽管它在过去的一些 WebKit 浏览器中(如旧版的 Safari 和 Chrome)得到了支持,但由于它并未成为 CSS 标准的一部分,因此在现代浏览器中的兼容性较差。以下是对 box-refl…...
ChatGPT 4o 使用案例之一
2024年GPT迎来重大更新,OpenAI发布GPT-4o GPT-4o(“o”代表“全能”) 它可以接受任意组合的文本、音频和图像作为输入,并生成任意组合的文本、音频和图像输出。它可以在 232 毫秒内响应音频输入,平均为 320 毫秒&…...

【免费Web系列】大家好 ,今天是Web课程的第一天点赞收藏关注,持续更新作品 !
开干,开干!!! 1. 前端开发介绍 我们介绍Web网站工作流程的时候提到,前端开发,主要的职责就是将数据以好看的样式呈现出来。说白了,就是开发网页程序,如下图所示: 那在讲解web前端开发之前,我们先需要对we…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
