rush 功能特性梳理
Rush 可以让 JavaScript 开发者更轻松地同时构建、发布多个 NPM 包,即将多个包或项目放到一个大仓库下管理。
仅需一次 NPM 安装
仅需一步,Rush 便可以将你项目的所有依赖安装到一个公共文件夹下,该文件夹并不像 “package.json” 一样位于项目的根目录(放到根目录的设计可能存在幻影依赖的问题),相反,Rush 使用符号链接来为每个项目重新构建一个准确的 “node_modules” 文件。
关于 “shrinkwrap 文件”
依据不同的包管理工具,shrinkwrap 文件可能是 shrinkwrap.yaml, npm-shrinkwrap.json, package-lock.json, 或 yarn.lock.(一些包管理工具使用了 “lock” 文件, 但该 “lock” 与文件的访问权限并无关系。在该文档中,由于我们并不知道你使用了哪种包管理工具,因此使用 “shrinkwrap” 来泛指这些文件。
通常,包管理工具会在每个项目文件夹内创建 shrinkwrap 文件,但是在 Rush 中,整个项目共用存储在 **common/config/rush" 目录下的一个 shrinkwrap 文件,它会被存储在 Git 内。 将所有依赖信息整合到单独一个 shrinkwrap 内有一些优势,例如减少冲突、方便查看 diff, 还能提高安装速度。
ensureConsistentVersions 依赖版本统一
我们推荐将 rush.json 内的 ensureConsistentVersions 设定为 true,它会使得 Rush 在执行操作包的指令时前执行 rush check。
该指令会去检查每个项目的 package.json 文件并保证所有的依赖都是同一个版本,该配置可以避免版本不一致导致的问题,因此推荐你打开。
npm分身
有时 node_modules 的数据结构会强制安装同一个包的两个相同版本的。这就相当于一个npm包有了分身。如B、C都依赖F1,E、F都依赖于F2,那么 node_modules 的数据结构有两种方式:要么安装两次F1(B、C node_modules下),一次F2(一级node_modules目录下),要么安装两次F2(E、F node_modules下),一次F1(一级node_modules目录下。
而 pnpm 解决了该问题。
幻影依赖
某个项目下引用了一个包,这个包不在其node_modules目录下,这种情况就是出现了幻影依赖。普通项目如果出现dependencies下的某个npm包依赖了其它包,则会自动在node_modules下被安装,这样项目中是可以直接引用这个其它包的,实际上在dependencies并没有这个其它包的声明,这样就出现了幻影依赖。而rush解决了这个问题。
而 rush 的符号链接解决了这个问题。
不建议在根目录安装npm包
在根目录放package.json且有依赖,执行npm i 后会产生node_modules目录,这样可能会造成幻影依赖。
指定rush的包管理器
基于幻影依赖和npm包分身,可以指定使用 pnpm 包管理器。
常用命令
# 安装所有项目依赖。会更新公共的 shrinkwrap 文件。
$ rush update# 与rush update 不同点是 rush install 不会更新任何文件,相反,如果存在过失的数据,则会在 PR 上报错,并提示你执行 rush update 或者提示你 commit 其结果。
$ rush install# 构建变动的项目。
$ rush build# 清空并构建所有项目。会默认查找每个项目的package.json的build命令并执行。
$ rush rebuild
rush update
当 package.json 文件发生变化时,请务必运行 rush update, 换句话说:
- 当从 git 上拉取新的更改(例如 git pull)后。
- 当项目内 package.json 文件被手动修改后。
- 当 common/config 目录下可能影响版本的文件(例如 pnpmfile.js, common-versions.json 等)被修改后。
rush update 内做了些什么:
- Rush 检查或应用各种可能会改变 common/config 内文件的策略。
- Rush 会将所有项目内的 package.json 文件与仓库的公共 shrinkwrap 文件进行比较来检查是否有效。
-
若无效,则包管理工具会更新 shrinkwrap 文件。 -
无论如何,包管理工具都会将所有依赖安装到 common/temp/node_modules 目录下。 - 最后,Rush 会给每个项目下构建一个 node_modules 文件夹,该文件夹下内容通过符合链接到 common/temp/node_modules. (该操作等同于 rush link)
相关文章:

rush 功能特性梳理
Rush 可以让 JavaScript 开发者更轻松地同时构建、发布多个 NPM 包,即将多个包或项目放到一个大仓库下管理。 仅需一次 NPM 安装 仅需一步,Rush 便可以将你项目的所有依赖安装到一个公共文件夹下,该文件夹并不像 “package.json” 一样位于项…...

算法分析与设计复习__递归方程与分治
总结自:【算法设计与分析】期末考试突击课_哔哩哔哩_bilibili 1.递归,递归方程 1.1递归条件: 1.一个问题的解可以分解为几个子问题的解; 2.这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样; 3.存在…...

apk-parse包信息解析
最近公司做项目,需要解析apk包的基本信息,上网找了好多资料,最终决定使用apk-parse。 .yml文件 引入jar包 <dependency> <groupId>net.dongliu</groupId> <artifactId>apk-parser</artifactId> <version&…...

AI绘画进阶工具ComfyUI 傻瓜整合包安装教程!模型共享,一键安装!
哈喽大家好,今天给大家分享一下AI绘画工具Stable Diffusion的另一种UI界面,常见的有: 窗口式界面的WebUI 节点式工作流的ComfyUI ComfyUI更加进阶一些,是一个节点式工作流的AI绘画界面,它高度可定制、自定义编辑Ai生…...
无人机摄影测量数据处理、三维建模及在土方量计算
原文链接:无人机摄影测量数据处理、三维建模及在土方量计算https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247603776&idx2&snd96440e116900a46a71c45ff77316896&chksmfa8217a7cdf59eb15da39dd6366378b98ca39b9c836b76a473ff292b67ee37a6ff6…...
)
大模型平台后端开发(xiaomi)
文章目录 算法题 算法题 1 三数之和 (注意去重的边界条件,过几天再刷几次) 2 长度最小的子数组 (代码随想录题目,滑动窗口) 3 用链表实现栈 package mainimport ("errors""fmt" )// Node 定义链表节点 type…...

性能测试工具—jmeter的基础使用
1.Jmeter三个重要组件 1.1线程组的介绍: 特点: 模拟用户,支持多用户操作多个线程组可以串行执行,也可以并行执行 线程组的分类: setup线程组:前置处理,初始化普通线程组:编写…...

前端 JS 经典:CommonJs 规范
1. Node 环境介绍 CommonJs 简称 CMJ,CMJ 的模块标准,必须在 node 的环境中才支持。在浏览器中用,是不行的。 查看电脑是否安装 node,通过打开终端,运行 node -v 查看是否返回 node 版本。返回则已安装。 CMJ 在 no…...

三分钟速览量化交易系统:揭秘QMT与Ptrade(内附免费提供渠道)
在当今金融市场的快速发展中,量化交易系统以其独特的优势,逐渐成为投资者们追求稳定收益的重要工具。其中,QMT和Ptrade作为两大知名的量化交易平台,受到了广泛关注。本文将带您在三分钟内快速了解量化交易系统,并深入揭…...

处理QTcpSocket接收到数据的槽函数
这段代码是一个典型的用于处理QTcpSocket接收到数据的槽函数 onReadyRead()。它尝试从发出信号的QTcpSocket读取数据,并将这些数据添加到一个成员变量 recvList(假设这是一个 QList<QString> 类型)。整体上,这段代码逻辑是合…...
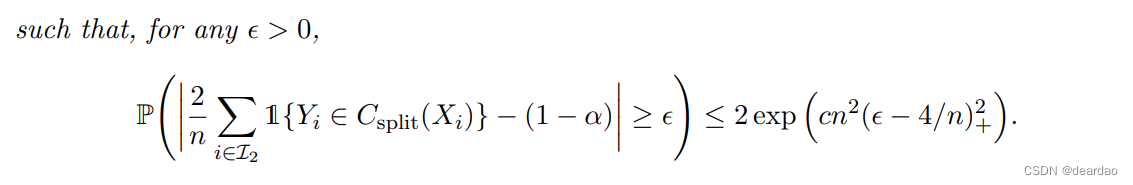
回归的无分布预测推理
摘要 我们利用保形推理,开发了回归中无分布预测推理的一般框架。所提出的方法允许使用回归函数的任何估计量构建响应变量的预测带。所得的预测带在标准假设下保留了原始估计量的一致性,同时保证了有限样本边际覆盖,即使这些假设不成立。我们…...

有限域中的一些概念
一、单位元: 在自然数中,任意数加上0等于本身,0则为加法的单位元,任意数乘以1等于本身,1则为乘法单位元。 有限域中单位元用e表示,即乘法,加法的单位元都用e表示,不过这两者的e不一样…...

使用css的box-reflect属性制作倒影效果
box-reflect 是一个在 CSS 中创建元素倒影效果的非标准属性。尽管它在过去的一些 WebKit 浏览器中(如旧版的 Safari 和 Chrome)得到了支持,但由于它并未成为 CSS 标准的一部分,因此在现代浏览器中的兼容性较差。以下是对 box-refl…...
ChatGPT 4o 使用案例之一
2024年GPT迎来重大更新,OpenAI发布GPT-4o GPT-4o(“o”代表“全能”) 它可以接受任意组合的文本、音频和图像作为输入,并生成任意组合的文本、音频和图像输出。它可以在 232 毫秒内响应音频输入,平均为 320 毫秒&…...

【免费Web系列】大家好 ,今天是Web课程的第一天点赞收藏关注,持续更新作品 !
开干,开干!!! 1. 前端开发介绍 我们介绍Web网站工作流程的时候提到,前端开发,主要的职责就是将数据以好看的样式呈现出来。说白了,就是开发网页程序,如下图所示: 那在讲解web前端开发之前,我们先需要对we…...
C++|树形关联式容器(set、map、multiset、multimap)介绍使用
目录 一、关联式容器介绍 1.1概念 1.2键值对 1.3树形结构的关联式容器 1.3.1pair模板介绍 1.3.2make_pair的介绍 二、set的介绍和使用 2.1set介绍 2.2set使用 2.2.1构造 2.2.2容量 2.2.3修改 三、map的介绍和使用 3.1map介绍 3.2map使用 3.2.1构造 3.2.2容量 …...

springboot整合s3,用ImageIO进行图片格式转换
上次用laravel进行了一些s3得整合,可以看出来其实蛮简单得。 先导包 <dependency><groupId>software.amazon.awssdk</groupId><artifactId>s3</artifactId></dependency> 然后在配置类中写bean private static final String …...

Windows 10无法远程桌面连接:原因及解决方案
在信息技术日益发展的今天,远程桌面连接已成为企业日常运维、技术支持乃至个人用户远程办公的必备工具。然而,有时我们可能会遇到Windows 10无法远程桌面连接的问题,这无疑会给我们的工作和生活带来诸多不便。 原因分析 1、远程访问未启用&a…...

图神经网络实战(10)——归纳学习
图神经网络实战(10)——归纳学习 0. 前言1. 转导学习与归纳学习2. 蛋白质相互作用数据集3. 构建 GraphSAGE 模型实现归纳学习小结系列链接 0. 前言 归纳学习 (Inductive learning) 通过基于已观测训练数据,建立一个通用模型,使模…...
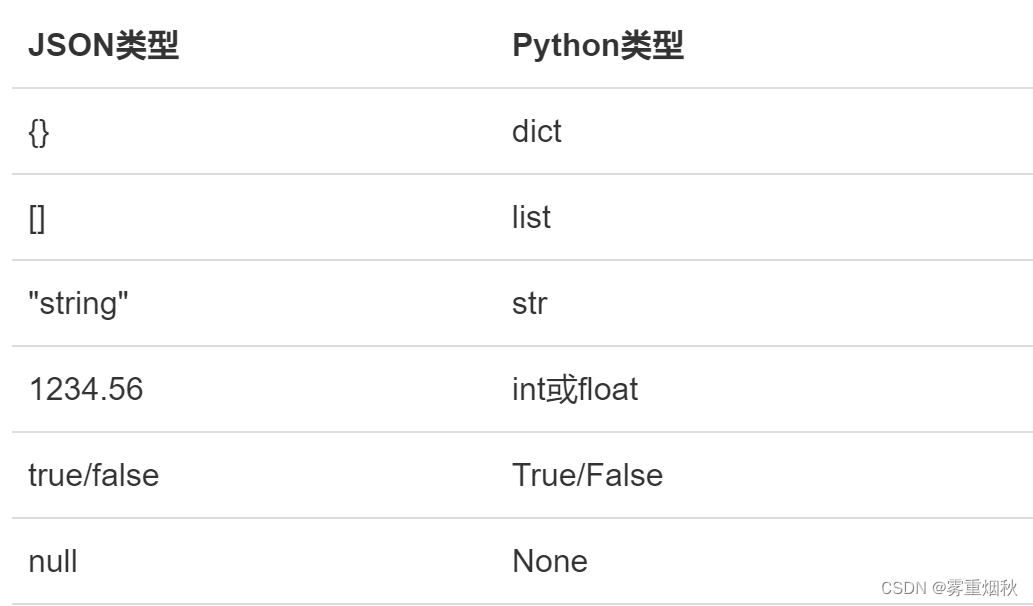
Python——IO编程
IO在计算机中指Input/Output,也就是输入和输出。由于程序和运行时数据是在内存中驻留,由CPU这个超快的计算核心来执行,涉及到数据交换的地方,通常是磁盘、网络等,就需要IO接口。 比如你打开浏览器,访问新浪…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
