牛客网刷题 | BC85 牛牛学数列3

目前主要分为三个专栏,后续还会添加:
专栏如下: C语言刷题解析 C语言系列文章 我的成长经历
感谢阅读!
初来乍到,如有错误请指出,感谢!
描述
牛牛准备继续进阶,计算更难的数列
输入一个整数n,计算 1+1/(1-3)+1/(1-3+5)+...+1/(1-3+5-...((-1)^(n-1))*(2n-1))的值
输入描述:
输入一个整数
输出描述:
输出一个浮点数,保留3位小数

题目解析 :
数列的公式是:
1+1/(1-3)+1/(1-3+5)+...+1/(1-3+5-...((-1)^(n-1))*(2n-1))
![]()
这个数列的每一项可以看作是一个分数,分子是1,分母是一个由奇数构成的序列,奇数的符号取决于项的位置是奇数还是偶数。具体来说:
- 当项的位置是奇数时,分母是正的奇数。
- 当项的位置是偶数时,分母是负的奇数。
因此,第k项可以表示为:


代码 1 :
别被难住了,分母看上去很长的样子,但如果我们仔细看,就会发现是 1-1/2+1/3这样,既然如此那代码就很简单了。
#include<stdio.h>
#include<math.h>
int main()
{int i = 0;double sum = 0;double q = 2.0;scanf("%d",&i);for(double j = 1;j<=i;j++){if(fmod(j, q) !=0){sum += (1/j);}elsesum -= (1/j);}printf("%.3lf\n",sum);return 0;
}
代码 2 :
//仔细观察不难发现分母其实是有规律的,我们不妨设一个变量来表示不断变化的分母
#include<stdio.h>
int main()
{int n,denominator=0,i;float sum=0;scanf("%d",&n);for (i=1;i<=n;i++){i%2==0?(denominator-=2*i-1):(denominator+=2*i-1);sum+=1.0/denominator;}printf("%.3f\n",sum);return 0;
}代码 3 :
#include <stdio.h>// 函数用于计算数列的第k项
double sequence_term(int k) {// 根据k的奇偶性,交替使用正负号double sign = (k % 2 == 0) ? 1 : -1;// 计算第k项的分母,即(2k-1)double denominator = sign * (2 * k - 1);// 返回第k项的值,分子是1return 1.0 / denominator;
}// 函数用于计算数列的和
double calculate_sequence_sum(int n) {double sum = 0.0; // 用于累加数列的和for (int k = 1; k <= n; ++k) {// 计算第k项,并累加到总和中sum += sequence_term(k);}return sum;
}int main() {int n;// 读取用户输入的整数nprintf("请输入一个整数n:");scanf("%d", &n);// 计算数列的和double sum = calculate_sequence_sum(n);// 输出结果,保留三位小数printf("数列的和为:%.3f\n", sum);return 0; // 程序结束
}代码 4 :
#include<stdio.h> // 引入标准输入输出库
#include<math.h> // 引入数学库,这里实际上不需要math.hint main() {int i = 0; // 声明一个整型变量i,用于存储项数double sum = 0; // 声明一个双精度浮点数变量sum,用于累加数列的和double q = 2.0; // 声明一个双精度浮点数变量q,实际上这里q的值应该是2,不需要是浮点数scanf("%d", &i); // 从标准输入读取一个整数,存储在变量i中for(double j = 1; j <= i; j++) { // 开始一个for循环,从1迭代到i// 修正逻辑:直接检查j是否为奇数,而不是使用fmodif((int)j % 2 != 0) { // 如果j是奇数sum += 1 / j; // 累加正项} else { // 如果j是偶数sum -= 1 / j; // 累加负项}}printf("%.3lf\n", sum); // 打印结果,保留三位小数return 0; // 程序执行成功,返回0
}知识点:pow函数
详见这篇文章
牛客网刷题 | BC83 牛牛学数列-CSDN博客
数列和序列:理解数列的概念,即一系列按照一定规律排列的数。
数学公式解析:解析给定的数学公式,并理解其数学意义。
条件表达式:使用条件表达式来确定数列中各项的符号,这涉及到奇偶性判断。
循环结构:使用循环结构来遍历数列的每一项,计算其值。
函数调用:在C语言中,使用 pow 函数来计算幂运算。
类型转换:在C语言中,进行类型转换以确保数学表达式中运算的准确性,例如,确保在进行除法运算时,至少有一个操作数是 double 类型。
输入输出操作:使用 scanf 进行输入操作,使用 printf 进行输出操作。
浮点数精度:处理浮点数时,理解精度问题,以及如何使用 %.3f 格式化输出来保留三位小数。
算法逻辑:设计算法来计算数列的和,这需要对数列的规律有清晰的认识。
代码结构:理解C语言的基本结构,包括函数定义、循环、条件语句等。
数学规律:识别并利用数学规律简化计算过程,例如,通过观察可以发现数列的符号交替出现,分母是递增的奇数。



相关文章:

牛客网刷题 | BC85 牛牛学数列3
目前主要分为三个专栏,后续还会添加: 专栏如下: C语言刷题解析 C语言系列文章 我的成长经历 感谢阅读! 初来乍到,如有错误请指出,感谢! 描述 牛牛准备继续进阶&…...
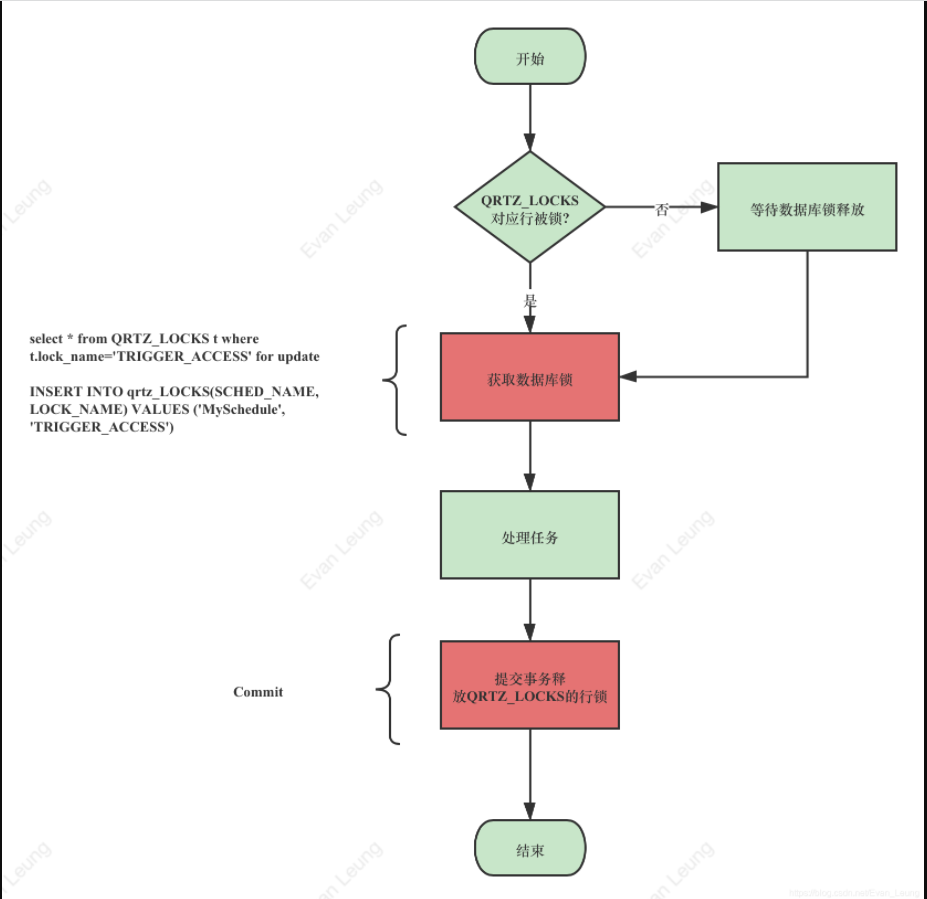
quartz定时任务
Quartz 数据结构 quartz采用完全二叉树:除了最后一层每一层节点都是满的,而且最后一层靠左排列。 二叉树节点个数规则:每层从左开始,第一层只有一个,就是2的0次幂,第二层两个就是2的1次幂,第三…...
——选择结构与循环结构)
Python基础学习笔记(五)——选择结构与循环结构
目录 程序的组织结构条件选择结构1. 单分支结构2. 双分支结构3. 多分支结构4. 嵌套(分支)结构5. 无内容执行6. 条件表达式 循环结构1. 可迭代对象2. range()函数3. for循环语句4. while循环语句5. 结束语句 程序的组织结构 程序的组织结构主要有以下三种…...

Vue插槽solt如何传递具名插槽的数据给子组件?
在Vue中,你可以通过作用域插槽(scoped slots)来传递数据给子组件。这同样适用于具名插槽。首先,你需要在子组件中定义一个具名插槽,并通过v-slot指令传递数据。例如: 子组件(ChildComponent.vu…...
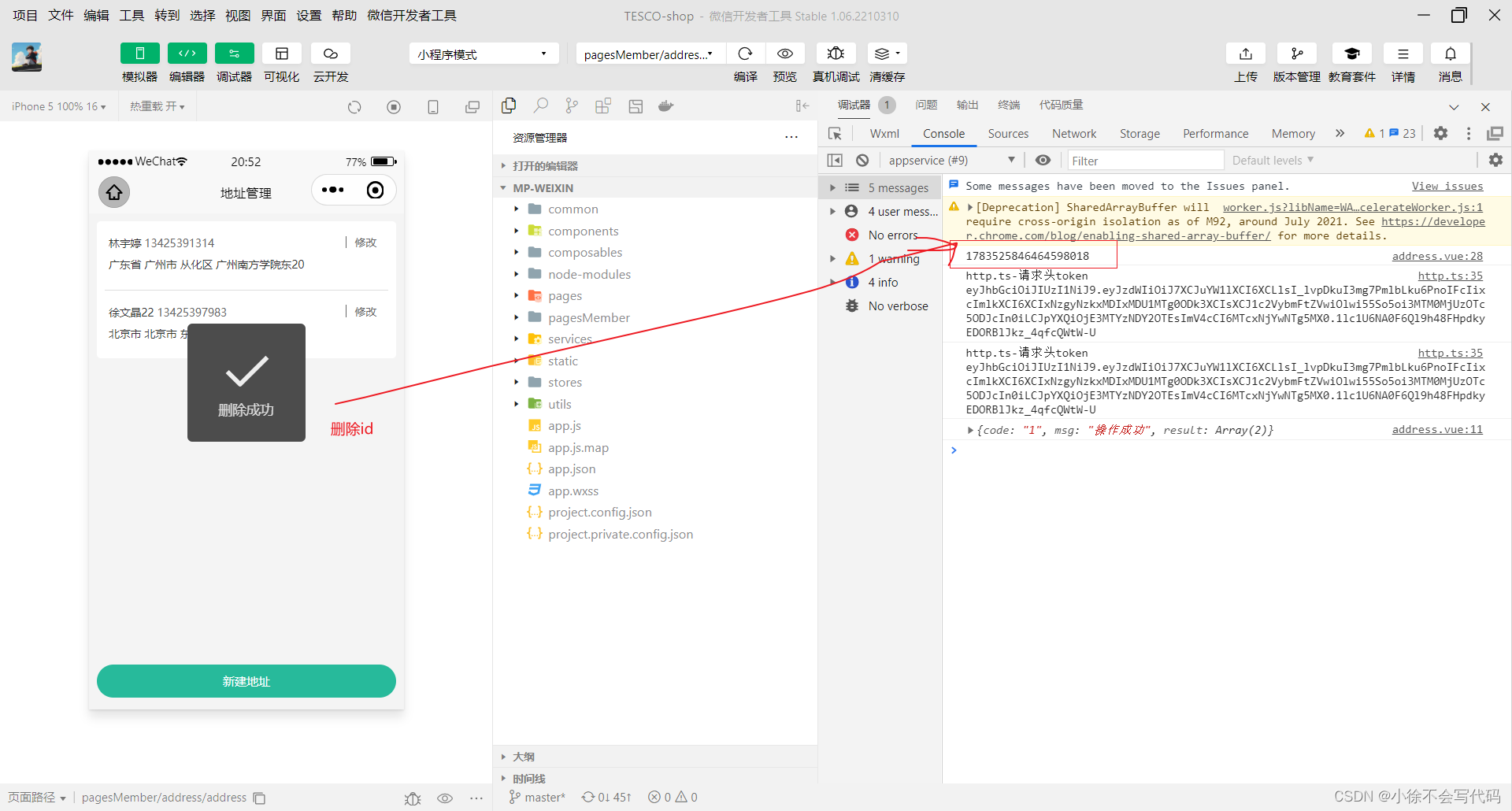
小程序-收货地址管理模块实现
页面结构代码: address-form.vue --->新建地址和修改地址页面 <template><view class"content"><form><!-- 表单内容 --><view class"form-item"><text class"label">收货人</text>…...
)
【星海随笔】微信小程序(三)
网络数据请求 1.小程序中网络数据请求的限制 出于安全性方面的考虑,小程序官方对 数据接口的请求 做出了如下 两个限制: ① 只能请求 HTTPS 类型的接口 ② 必须将 接口的域名 添加到 信任列表 中 微信小程序只能请求 https 类型的接口 且需要请求的域名必须提前进行设置后,才可…...
pip(包管理器) for Python
pip是什么 pip是Python的包安装程序,即python包管理器。您可以使用 pip 从Python包索引和其他索引安装包。 1. pip 安装 python 包 pip install 包名 例如:pip install pymssql : 使用pip安装数据库驱动包 pymssql 2.pip 卸载 python 包 pi…...

Ubuntu上安装Maven
在Ubuntu上安装Maven的步骤如下: 更新包索引: sudo apt update 安装Maven: sudo apt install maven 验证安装是否成功: mvn -version 以上步骤将会安装Maven并添加到系统路径中,你可以通过运行mvn -version来验…...
java中使用svnkit实现文件的版本管理
java中使用svnkit实现文件的版本管理 一、引入svnKit依赖二、初始化仓库工厂类二、使用svnkit创建本地存储仓库三、svn基本原子操作四、通过原子方法实现简单svn相应操作 一、引入svnKit依赖 <dependency><groupId>org.tmatesoft.svnkit</groupId><artifa…...
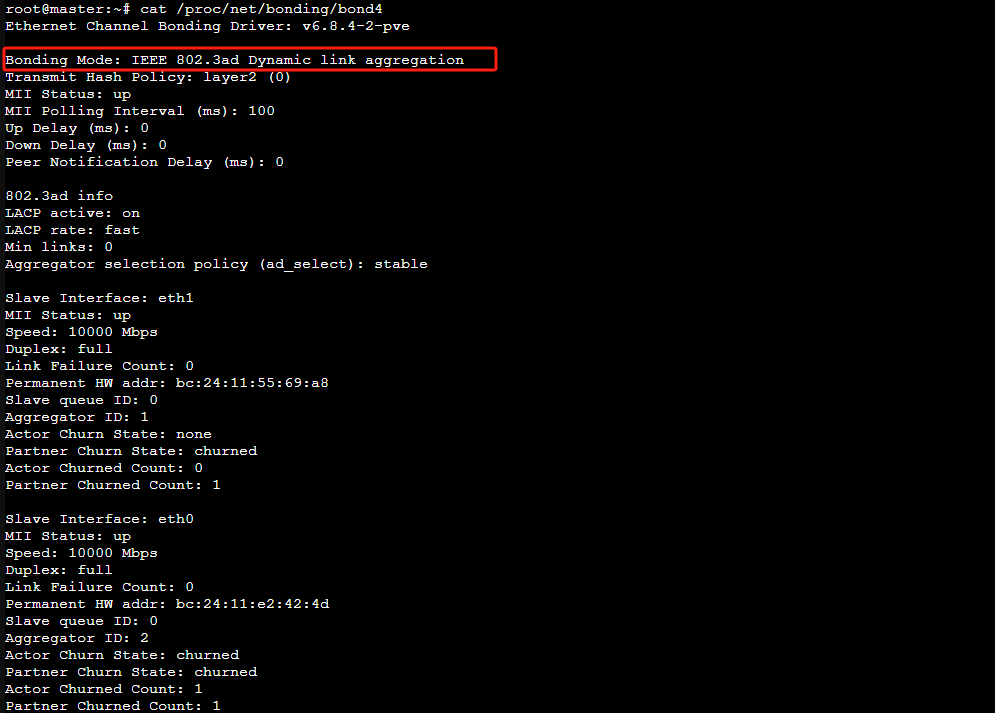
了解 Linux 网络卡绑定:提高网络性能与冗余性
在现代 IT 基础设施中,网络性能和可靠性至关重要。对于许多企业和个人用户来说,确保网络的高可用性和冗余性是首要任务之一。Linux 提供了一个强大的解决方案——网络卡绑定(Network Interface Card Bonding,简称 NIC Bonding&…...

2024年618购物狂欢节即将来袭!精选五款超值入手数码好物!
618购物狂欢盛宴即将落幕,是时候展现我们的购物智慧了!在追求价格优惠的同时,我们更应看重商品的品质与实用性。面对琳琅满目的选择,如何筛选出真正值得拥有的好物呢?为了让大家的购物之旅更加轻松愉快,以下…...

中国AI独角兽资本大冒险
成立不过一年多时间,月之暗面已然成为中国大模型赛道上,最炙手可热的明星公司。 5月21日,华尔街见闻获悉,月之暗面将按照投前估值30亿美元(合217.3亿人民币)进行融资,完成后依然会是当前中国估…...
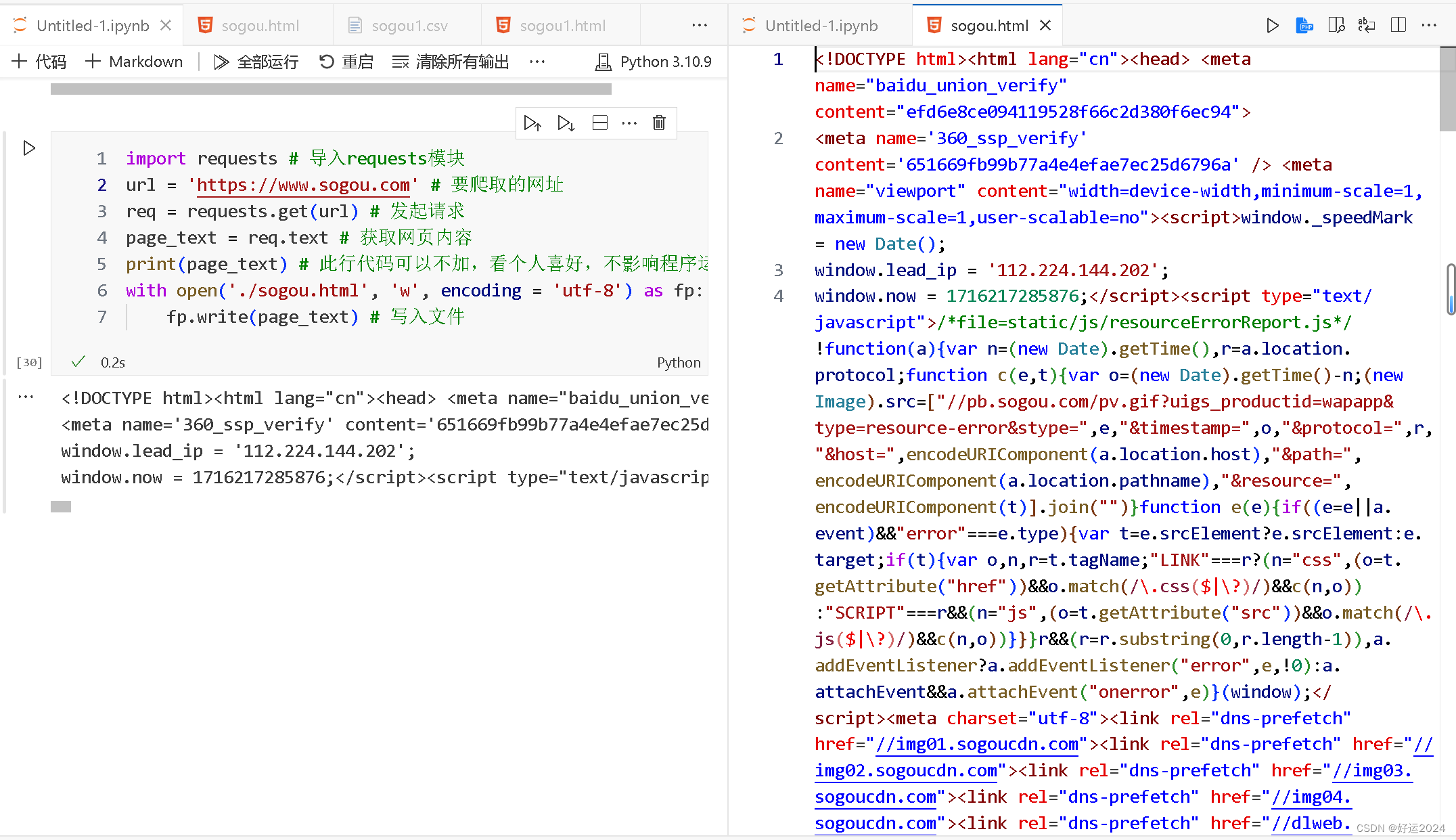
项目十二:简单的python基础爬虫训练
许久未见,甚是想念,今日好运,为你带好运。ok,废话不多说,希望这门案例能带你直接快速了解并运用。🎁💖 基础流程 第一步:安装需要用到的requests库,命令如下 pip inst…...

OpenGL学习入门及开发环境搭建
最近学习OpenGL开发,被各种openGL库搞得晕头转向,什么glut, glew glfw glad等等。 可以参考这边博客:OpenGL 下面的 glut freeglut glfw 都是个啥_glx wgl的中文-CSDN博客 glfw是glut的升级版,跨平台的主要处理窗口 事件相关。 glad是glew…...

three.js能实现啥效果?看过来,这里都是它的菜(08)
在Three.js中实现旋转动画的原理是通过修改对象的旋转属性来实现的,通常使用渲染循环(render loop)来更新对象的旋转状态,从而实现动画效果。 具体的原理包括以下几个步骤: 创建对象:首先创建一个需要旋转…...
之整合mybatis)
SpringBoot(九)之整合mybatis
SpringBoot(九)之整合mybatis 文章目录 SpringBoot(九)之整合mybatisSpring整合mybatis回顾1. 引入依赖2. mybatis-config.xml SpringBoot整合mybatis1.引入依赖2. 配置数据源和 MyBatis 属性3. 配置 Mapper 接口4. 配置mapper.xm…...

【实战教程】使用Spring AOP和自定义注解监控接口调用
一、背景 随着项目的长期运行和迭代,积累的功能日益繁多,但并非所有功能都能得到用户的频繁使用或实际上根本无人问津。 为了提高系统性能和代码质量,我们往往需要对那些不常用的功能进行下线处理。 那么,该下线哪些功能呢&…...

算法学习之:Raft-分布式一致性/共识算法
基础介绍 Raft是什么? Raft is a consensus algorithm that is designed to be easy to understand. Its equivalent to Paxos in fault-tolerance and performance. The difference is that its decomposed into relatively independent subproblems, and it clea…...

彩色进度条(C语言版本)
.h文件 #include<stdio.h> #include<windows.h>#define NUM 101 #define LOAD_UP 50 #define LOAD_DOWN 60 #define SLEEP_SLOW 300 #define SLEEP_FAST 70 版本1:(初始版) //v1 #include "progress.h" int main() …...

C#和C++有什么区别?
C#和C都是广泛使用的编程语言,但它们在设计理念、应用场景和语法上有许多显著的区别。以下是一些关键区别的详细介绍: 1. 设计理念和目的 C: 设计目的:C是一种面向系统编程和应用程序开发的语言,具有高效性和灵活性…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
