【代码随想录 二叉树】二叉树前序、中序、后序遍历的迭代遍历
文章目录
- 1. 二叉树前序遍历(迭代法)
- 2. 二叉树后序遍历(迭代法)
- 3. 二叉树中序遍历(迭代法)
1. 二叉树前序遍历(迭代法)
题目连接
🍎因为处理顺序和访问顺序是一致的。所以方便处理!
- 示例代码如下所示:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {stack<TreeNode*> st; // 栈:后进先出,满足递归想要获取上一个位置的逻辑vector<int> ans;if (root == nullptr)return ans;st.push(root);while (!st.empty()){TreeNode* node = st.top();ans.push_back(node->val);st.pop();// 为什么先弹入右节点呢 ? (因为栈是后进先出的)if (node->right != nullptr){st.push(node->right);}if (node->left != nullptr){st.push(node->left);}}return ans;}
};
2. 二叉树后序遍历(迭代法)
题目链接🔗

class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st; // 栈:后进先出,满足递归想要获取上一个位置的逻辑vector<int> ans;if (root == nullptr)return ans;st.push(root);while (!st.empty()){TreeNode* node = st.top();ans.push_back(node->val);st.pop();//只需要改一下左右子树的遍历顺序即可if (node->left != nullptr){st.push(node->left);}if (node->right != nullptr){st.push(node->right);}}reverse(ans.begin(), ans.end());return ans;}
};
3. 二叉树中序遍历(迭代法)
题目链接🔗
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st; // 栈:后进先出,满足递归想要获取上一个位置的逻辑vector<int> ans;if (root == nullptr)return ans;st.push(root);while (!st.empty()){TreeNode* node = st.top();ans.push_back(node->val);st.pop();if (node->left != nullptr){st.push(node->left);}if (node->right != nullptr){st.push(node->right);}}reverse(ans.begin(), ans.end());return ans;}
};

相关文章:

【代码随想录 二叉树】二叉树前序、中序、后序遍历的迭代遍历
文章目录 1. 二叉树前序遍历(迭代法)2. 二叉树后序遍历(迭代法)3. 二叉树中序遍历(迭代法) 1. 二叉树前序遍历(迭代法) 题目连接 🍎因为处理顺序和访问顺序是一致的。所…...

Error:(6, 43) java: 程序包org.springframework.data.redis.core不存在
目录 一、在做SpringBoot整合Redis的项目时,报错: 二、尝试 三、解决办法 一、在做SpringBoot整合Redis的项目时,报错: 二、尝试 给依赖加版本号,并且把版本换了个遍,也不行,也去update过ma…...
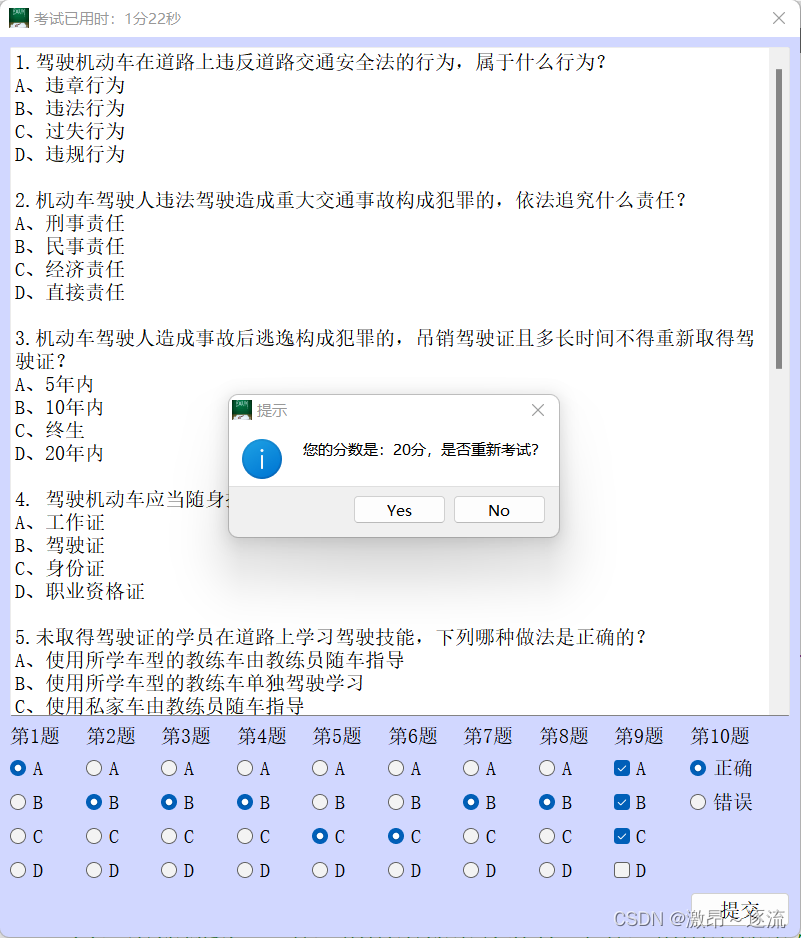
Qt 科目一考试系统(有源码)
项目源码和资源:科目一考试系统: qt实现科目一考试系统 一.项目概述 该项目是一个基于Qt框架开发的在线考试系统,主要实现了考试题目的随机抽取、考试时间限制、成绩统计等功能。用户可以通过界面操作进行考试,并查看自己的考试成绩。 二.技…...

在 Visual Studio 2022 (VS2022) 中删除 Git 分支的步骤如下
git branch -r PS \MauiApp1> git push origin --delete “20240523备份” git push origin --delete “20240523备份”...

玩转OpenHarmony智能家居:如何实现开发版“碰一碰”设备控制
一、简介 “碰一碰”设备控制,依托NFC短距通信协议,通过碰一碰的交互方式,将OpenAtom OpenHarmony(简称“OpenHarmony”)标准系统设备和全场景设备连接起来,解决了应用与设备之间接续慢、传输难的问题&…...

订餐系统总结、
应用层: SpringBoot:快速构建Spring项目,采用“约定大于配置”的思想,简化Spring项目的配置开发。 SpringMvc:Spring框架的一个模块,springmvc和spring无需通过中间整合层进行整合,可以无缝集成。 Sprin…...

【因果推断从入门到精通二】随机实验3
目录 检验无因果效应假说 硬币投掷的特殊性何在? 检验无因果效应假说 无因果效应假说认为,有些人存活,有些人死亡,但接受mAb114治疗而不是ZMapp与此无关。在174例接受mAb14治疗的患者中,113/17464.9%存活了28天&…...
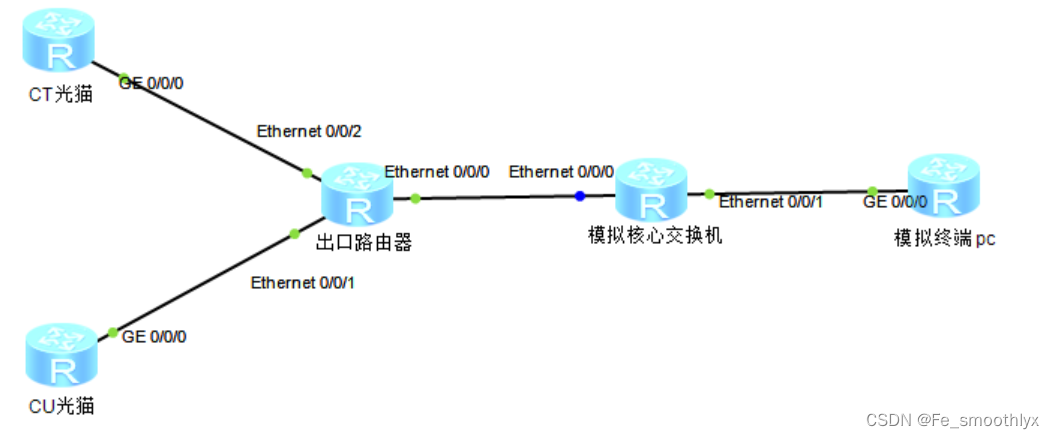
真实案例分享,终端pc直接telnet不到出口路由器。
1、背景信息 我终端pc的网卡地址获取的网关是在核心交换机上,在核心交换机上telnet出口路由器可以实现。 所有终端网段都不能telnet出口路由器,客户希望能用最小的影响方式进行解决。 2、现有配置信息 终端的无线和有线分别在两个网段中,…...

YOLOv8_seg的训练、验证、预测及导出[实例分割实践篇]
实例分割数据集链接,还是和目标检测篇一样,从coco2017val数据集中挑出来person和surfboard两类:链接:百度网盘 请输入提取码 提取码:3xmm 1.实例分割数据划分及配置 1.1实例分割数据划分 从上面得到的数据还不能够直接训练,需要按照一定的比例划分训练集和验证集,并按…...

Linux基础(四):Linux系统文件类型与文件权限
各位看官,好久不见,在正式介绍Linux的基本命令之前,我们首先了解一下,关于文件的知识。 目录 一、文件类型 二、文件权限 2.1 文件访问者的分类 2.2 文件权限 2.2.1 文件的基本权限 2.2.2 文件权限值的表示方法 三、修改文…...

本是梦中人,常作花下客。心中自往来,知我有几个。
我们总是喜欢拿“顺其自然”来敷衍人生道路上的荆棘坎坷,却很少承认,真正的顺其自然, 其实是竭尽所能之后的不强求, 而非两手一摊的不作为。 一花凋零荒芜不了整个春天, 一次挫折也荒废不了整个人生。 多年后&#x…...

创新指南|利用电商产品视频进行渠道营销的最佳策略,不断提升销售额
无论企业的利基市场如何,电商产品视频都已被证明是非常可靠的资产,可以让目标受众了解您所提供的产品——关键功能、展示重要的差异化优势甚至改变大多数营销活动的游戏规则。阅读本文,全面了解电商产品视频如何融入营销推广,以最…...
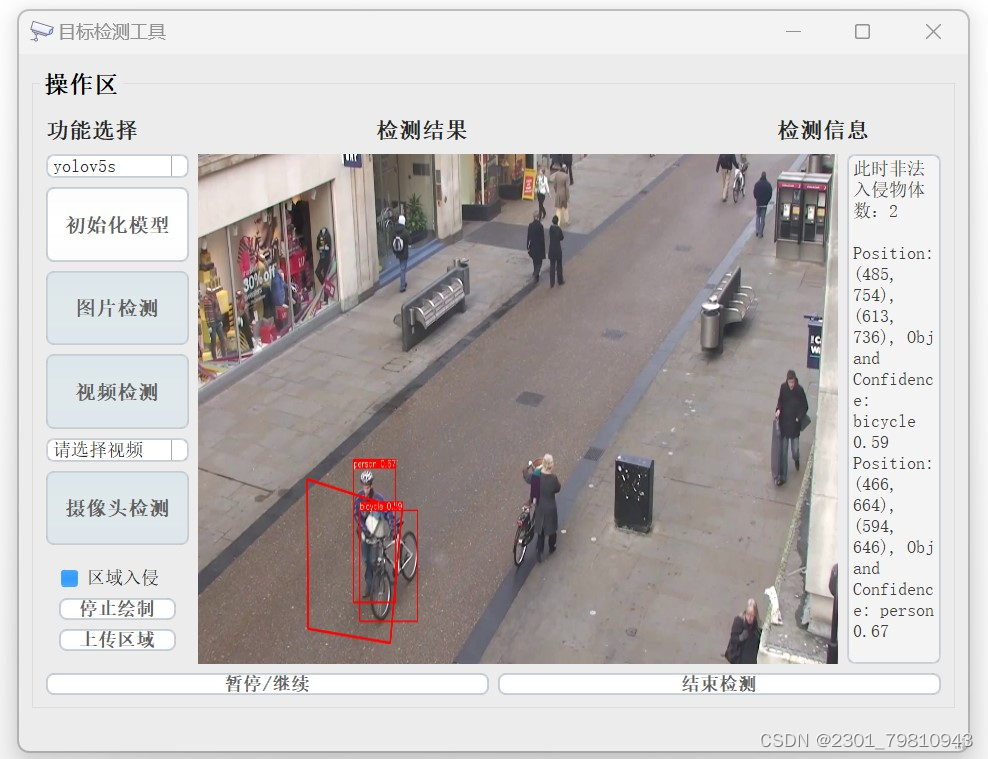
深度学习之基于YoloV5入侵检测系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景 随着信息技术的飞速发展,网络安全问题日益凸显。入侵检测系统(IDS࿰…...
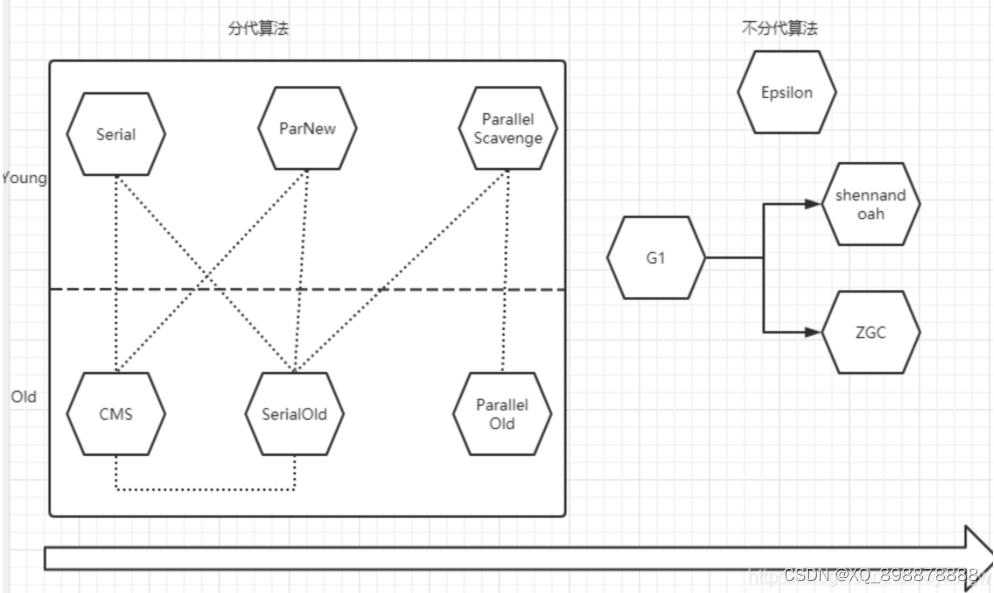
【01】全面理解JVM虚拟机
一、前言 学习JVM是进行JVM调优的基础。写的代码部署到线上它会如何运行?要配多少内存?线上环境出问题了,服务崩溃了,应该怎么快速定位?这些问题都与JVM有着一定的关系。好的程序员都应该尽自己的能力把JVM每个底层逻…...
CentOS7离线安装Nginx
目录 1. 安装gcc2. 安装g3. 安装openssl4. 安装pcre5. 安装zlib6. 安装Nginx7. 启动nginx8. 开放80端口9. 访问测试10. 设置开机自启 Nginx离线安装需要依赖gcc、g环境,安装前要先检查linux系统中是否自带gcc和g,如果没有就需要先进行安装。 然后再安装o…...

面试字节大模型算法实习岗,感觉有点崩溃。。。
节前,我们组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。 针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。 总结链接…...
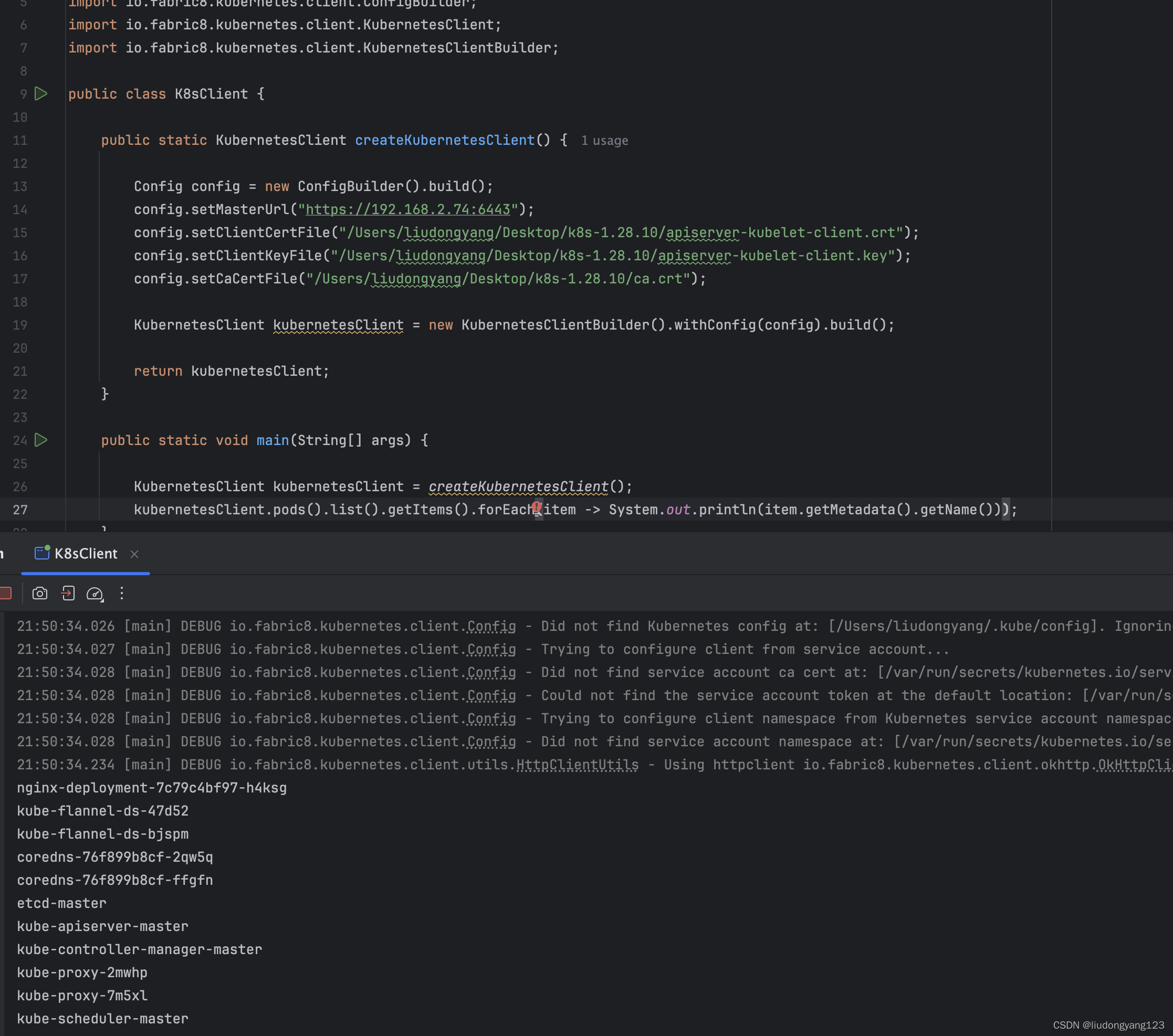
k8s 1.24.x之后如果rest 访问apiserver
1.由于 在 1.24 (还是 1.20 不清楚了)之后,下面这两个apiserver的配置已经被弃用 了,简单的说就是想不安全的访问k8s是不可能了,所以只能走安全的访问方式也就是 https://xx:6443了,所以需要证书。 - --ins…...

深度解析:用 Python 爬虫逆向破解 solscan 的请求头加密参数 Sol-Aut
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 逆向是爬虫工程师进阶必备技能,当我们遇到一个问题时可能会有多种解决途径,而如何做出最高效的抉择又需要经验的积累。本期文章将以实战的方式,带你详细地逆向分析 solscan 网站请求头加密字段 Sol-Aut 的构造逻辑,…...

Flutter 中的 InputDecorator 小部件:全面指南
Flutter 中的 InputDecorator 小部件:全面指南 在Flutter中,InputDecorator是一个用于装饰输入字段的组件,它为TextField和TextFormField提供了一个统一的外观和布局。InputDecorator可以让您自定义输入框的标签、填充、边框、图标、光标、错…...

useTransition:开启React并发模式
写在前面:并发 并发模式(Concurrent Mode)1的一个关键特性是渲染可中断。 React 18 之前,更新内容渲染的方式是通过一个单一的且不可中断的同步事务进行处理。同步渲染意味着,一旦开始渲染就无法中断,直到…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
