C语言章节学习归纳--数据类型、运算符与表达式
3.1 C语言的数据类型(理解)
首先,对变量的定义可以包括三个方面:
数据类型
存储类型
作用域
所谓数据类型是按被定义变量的性质,表示形式,占据存储空间的多少,构造特点来划分的。在C语言中,数据类型可分为:基本数据类型,构造数据类型,指针类型,空类型四大类。
熟记下面这个导图即可
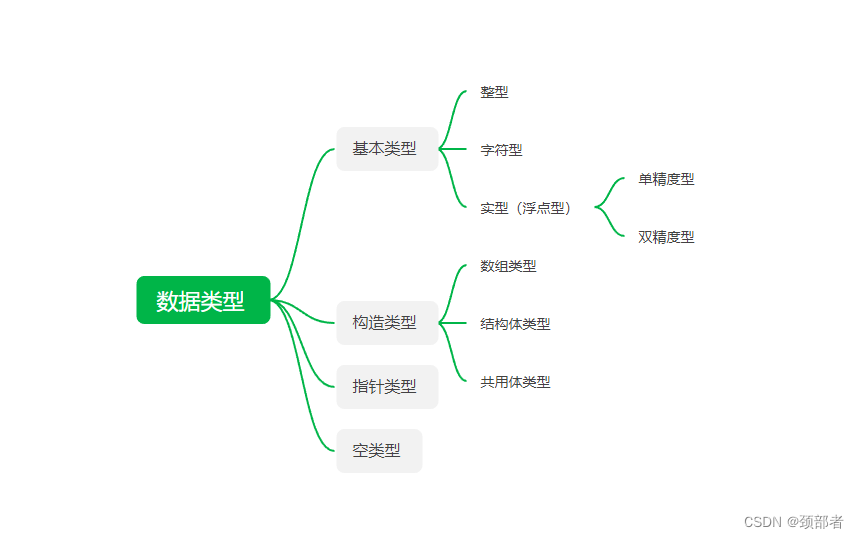
1.基本数据类型:基本数据类型最重要的特点是,其值不可以再分解为其它类型。也就是说,基本数据类型是自我说明的。
2.构造数据类型:构造数据类型是根据已定义的一个或多个数据类型用构造的方法来定义的。也就是说,一个构造类型的值可以分解成若干个“成员”或“元素”。每个“成员”都是一个基本数据类型或又是一个构造类型。在C语言中,构造类型有以下几种:
数组类型
结构体类型
共用体(联合)类型
3.指针类型:指针是一种特殊的,同时又是具有重要作用的数据类型。其值用来表示某个变量在内存存储器中的地址。虽然指针变量的取值类似于整型量,但这是两个类型完全不同的量,因此不能混为一谈。
4.空类型:在调用函数值时,通常应向调用者返回一个函数值。这个返回的函数值是具有一定的数据类型的,应在函数定义及函数说明中给以说明,例如在例题中给出的max函数定义中,函数头为:int max(int a,int b);其中“int”类型说明符即表示该函数的返回值为整型量。又如在例题中,使用了库函数sin,由于系统规定其函数返回值为双精度浮点型,因此在赋值语句s=sin(x);中,s也必须是双精度浮点型,以便与sin函数的返回值一致。所以在说明部分,把s说明为双精度浮点型。但是,也有一类函数,调用后并不需要向调用者返回函数值,这种函数可以定义为“空类型”。其类型说明符为void。在后面函数中还要详细介绍。
3.2 常量与变量(理解)
对于基本数据类型量,按其取值是否可改变又分为常量和变量两种。在程序执行过程中,其值不发生改变的量称为常量,其值可变的量称为变量。它们可与数据类型结合起来分类。例如,可分为整型常量、整型变量、浮点常量、浮点变量、字符常量、字符变量、枚举常量、枚举变量。在程序中,常量是可以不经说明而直接引用的,而变量则必须先定义后使用。
整型量包括整型常量、整型变量。
3.2.1 常量和符号变量
在程序执行过程中,其值不发生改变的量称为常量。
直接常量(字面常量):
整型常量:12,0,-4;
实型常量:4.6、-1.23;
字符常量:‘a’、'b'。
标识符:用来标识变量名、符号常量名、函数名、数组名、类型名、文件名的有效字符序列。
符号常量:用标示符代表一个常量。在c语言中,可以用一个标识符来表示一个常量,称之为符号常量。
符号常量在使用之前必须先定义,其一般形式为:
#define 标识符 常量
其中#define也是一条预处理命令(预处理命令都以“#”开头),称为宏定义命令(在后面预处理程序中将进一步介绍),其功能是把该标识符定义为其后的常量值。一经定义,以后在程序中所有出现该标识符的地方均代之以该常量值。
习惯上符号常量的标识符用大写字母,变量标识符用小写字母,以示区别。
#include<stdio.h>
#define PRICE 30
int main()
{int num,total;num = 10;total = num * PRICE;printf("total = %d",total);return 0;
}用标识符代表一个常量,称为符号常量。
符号常量与变量不同,它的值在其作用域内不能改变,也不能再被赋值。
使用符号常量的好处是:
含义清楚;
能做到“一改全改”。
常量导图如图所示:

3.2.2 变量
其值可以改变的量称为变量。一个变量应该有一个名字,在内存中占据一定的存储单元。变量定义必须放在变量使用之前。一般放在函数体的开头部分。要区分变量名和变量值是两个不同的概念。

3.3 整型数据(掌握)
3.3.1 整型常量的表示方法(必考点)
学习提示:
掌握八进制、十六进制、十进制合法表示。要一眼看出来这个数是不是合法表示,是八进制还是十六进制还是十进制。
掌握八进制、十六进制、十进制以及二进制的相互转换。
整型常量就是整常数。在c语言中,使用的整常数有八进制、十六进制和十进制三种。
十进制整常数:十进制整常数没有前缀。其数码为0~9。
以下是合法的十进制整常数:
230,-4512,65535、1258;
以下各数不是合法的十进制整常数:
023(不能有前导0)、23D(含有非十进制数码)。
在程序中是根据前缀来区分各种进制数的。因此在书写常数时不要把前缀弄错造成结果不正确。
八进制整常数:八进制整常数必须以0开头,即以0作为八进制数的前缀。数码取值为0~7。八进制数通常是无符号数。
以下各数是合法的八进制数:
015(十进制为13)、0101(十进制为65)、0177777(十进制为65535);
以下各数不是合法的八进制数:
256(无前缀0)、03A2(包含了非八进制数码A)、-0124(出现了负号)。
十六进制整常数:十六进制整常数的前缀为0X或0x。其数码取值为0~9,A~F或a~f。
以下各数是合法的十六进制整常数:
0X2A(十进制为42)、0XA0(十进制为160)、0XFFFF(十进制为65535);
以下各数不是合法的十六进制整常数:
5A(无前缀0X)、0X3H(含有非十六进制数码)。
整型常数的后缀:在16位字长的机器上,基本整型的长度也为16位,因此表示的数的范围也是有限定的。十进制无符号整常数的范围为0~65535,有符号数为-32768~+32767。八进制无符号数的表示范围为0~0177777。十六进制无符号数的表示范围为0X0~0XFFFF或0x0~0xFFFF。如果使用的数超过了上述范围,就必须用长整型数来表示。长整型数是用后缀“L”或“I”来表示的。
例如:
十进制长整常数:
158L(十进制为158)、358000L(十进制为358000)
八进制长整常数:
012L(十进制为10)、077L(十进制为63);、0200000L(十进制为65536);
十六进制长整常数:
0X15L(十进制为21)、0XA5L(十进制为165)、0X10000L(十进制为65536);
长整数158L和基本整常数158在数值上并无区别。但对158L,因为是长整型量,C编译系统将它分配4个字节存储空间。而对158,因为是基本整型,只分配2个字节的存储空间。因此在运算和输出格式上要予以注意,避免出错。
无符号数也可用后缀表示,整型常数的无符号数的后缀为“U”或“u”。
例如:
358u,0x38Au,235Lu均为无符号数。
前缀,后缀可同时使用以表示各种类型的数。如0XA5Lu表示十六进制无符号长整数A5,其十进制为165。
3.3.2 整型变量(理解)
1.整型数据在内存中的存放形式(了解)
定义了一个整型变量i:
int i;
i = 10;
提示:任何数据的存放都是二进制形式
原码补码相关概念,大家可以去搜一下,初学者了解即可。
本来是有图的,但太麻烦了我就没弄,大家自行理解哈。
数值是以补码表示的:
1:正数的补码和原码相同;
2:负数的补码:将该数的绝对值的二进制形式按位取反再加1。
2.整型变量的分类(理解)
以下数据类型的字节数与计算机系统有关。16位、32位或者64位系统,int ,long等类型的字节数可能不同。
如果感兴趣,可以自行编程计算手机环境中各类型的字节数。int a;sizeof(a)即可求出int类型的字节数。其他类型类似。
1基本型:类型说明符为int,在内存中占2个字节。
2短整量:类型说明符为short int或short。所占字节和取值范围均与基本型相同。
3长整型:类型说明符为long int 或long,在内存中占4个字节。
4无符号型:类型说明符为unsigned。
无符号型又可与上述三种类型匹配而构成:
1无符号基本型:类型说明符为unsigned int或unsigned。
2无符号短整型:类型说明符为unsigned short。
3无符号长整型:类型说明符为unsigned long。
各种无符号类型量所占的内存空间字节数与相应的有符号类型量相同。但由于省去了符号位,故不能表示负数。
3.整型变量的定义(理解)
变量定义的一般形式为:
类型说明符 变量名标识符,变量名标识符,。。。;
例如:
int a,b,c;(a,b,c为整型变量)
long x,y;(x,y为长整型变量)
unsigned p,q;(p,q为无符号整型变量)
在书写变量定义时,应注意以下几点:、
允许在一个类型说明符后,定义多个相同类型的变量。各变量名之间用逗号间隔。类型说明符与变量名之间至少用一个空格间隔。
最后一个变量名之后必须以“;”号结尾。
变量定义必须放在变量使用之前。一般放在函数体的开头部分。
例3.2整型变量的定义与使用。
#include <stdio.h>int main()
{int a,b,c,d;unsigned u;a = 12;b = -24;u = 10;c = a + u;d = b + u;printf("a + u = %d,b + u = %d\n",c,d);return 0;
}运行结果:

4.整型数据的溢出
例3.3 整型数据的溢出。
#include <stdio.h>int main()
{int a,b;// 整数最大值16位时为32767,32位是2147483647,64位9223372036854775807。// 所以此题运行结果与编译器环境有关a = 2147483647;b = a+1;printf("%d,%d\n",a,b);return 0;
}编译结果

可看出我使用的这个在线编译器是32位的
例3.4 类型自动转换
#include <stdio.h>int main()
{long x,y;int a,b,c,d;x = 5;y = 6;a = 7;b = 8;c = x+a;d = y+b;printf("c=x+a=%d,d=y+b=%d\n",c,d);return 0;
}运行结果:

从程序中可以看到:x,y是长整型变量,a,b是基本整型变量。它们之间允许进行运算,运算结果为长整型。但c,d被定义为基本整型,因此最后结果为基本整型。本例说明,不同类型的量可以参与运算并相互赋值。其中的类型转换是由编译系统自动完成的。有关类型转换的规则将在以后介绍。
3.4 实型数据
3.4.1 实型常量的表示方法(掌握)
实型也称为浮点型。实型常量也称为实数或者浮点数。在C语言中,实数只采用十进制。它有两种形式:十进制小数形式,指数形式。
1十进制数形式:由数码0~9和小数点组成。
例如:
0.0、25.0、5.789、0.13、5.0、300、-267.8230
等均为合法的实数。注意:必须有小数点。
2指数形式(考点):由十进制数,加阶码标志“e”或“E”以及阶码(只能为整数,可以带符号)组成。
其一般形式为:
a E n (a为十进制数,n为十进制整数)
其值为a*10^n(10^n意思为10的n次方,以下相同)。
如:
2.1E5(等于2.1*10^5)
3.7E-2(等于3.7*10^-2)
0.5E7(等于0.5*10^7)
-2.8E-2(等于-2.8*10-2)
以下不是合法的实数:
345(无小数点)
E7(阶码标志E之前无数字)
-5(无阶码标志)
53.-E3(负号位置不对)
2.7E(无阶码)
标准C允许浮点数使用后缀。后缀为“f”或“F”即表示该数为浮点数。如356f和356.是等价的。
例3.5说明了这种情况。
#include <stdio.h>int main()
{printf("%f\n",356.);printf("%f\n",356);printf("%f\n",356f);return 0;
}我在编译网站上编译这个的时候发现报错了


网上找的答案,可能这个网站不是标准C吧,不允许这样用?有了解的朋友可以在评论区回答一下
3.4.2实型变量
1.实型数据在内存中的存放形式(了解)
实型数据一般占4个字节(32位)内存空间。按指数形式存储。
2.实型变量的分类(掌握)
实型变量分为:单精度(float型)、双精度(double型)和长双精度(long double型)三类。
在Turbo C中单精度型占4个字节(32位)内存空间,其数值范围为3.4E-38~3.4E+38,只能提供七E位有效数字。双精度型占8个字节(64位)内存空间,其数值范围为1.7E-308~1.7E+308,可提供16位有效数字。
实型变量定义的格式和书写规则与整型相同。
例如:
float x,y;(x,y为单精度实型量)
double a,b,c;(a,b,c为双精度实型量)
3.实型数据的舍入误差(理解)
由于实型变量是由有限的存储单元组成的,因此能提供的有效数字总是有限的。如下例。
例3.6实型数据的舍入误差。
#include <stdio.h>int main()
{float a,b;a = 123456.789e5;b = a + 20;printf("%f\n",a);printf("%f\n",b);return 0;
}运行结果:

注意:1.0/3*3的结果并不等于1.
#include <stdio.h>int main()
{float a;double b;a = 33333.33333;b = 33333.33333333333333;printf("%f\n%f\n",a,b);return 0;
}运行结果:

从本例可以看出,由于a是单精度浮点型,有效位数只有七位。而整数已占五位,故小数二位后之后均为无效数字。
b是双精度型,有效位为十六位。但Turbo C规定小数后最多保留六位,其余部分四舍五入。
3.4.3 实型常数的类型
实型常数不分单、双精度,都按双精度double型处理。
将近半个小时整理了1/3,剩下的明天下午整理完全,预估两个小时。晚安
相关文章:

C语言章节学习归纳--数据类型、运算符与表达式
3.1 C语言的数据类型(理解) 首先,对变量的定义可以包括三个方面: 数据类型 存储类型 作用域 所谓数据类型是按被定义变量的性质,表示形式,占据存储空间的多少,构造特点来划分的。在C语言中&…...
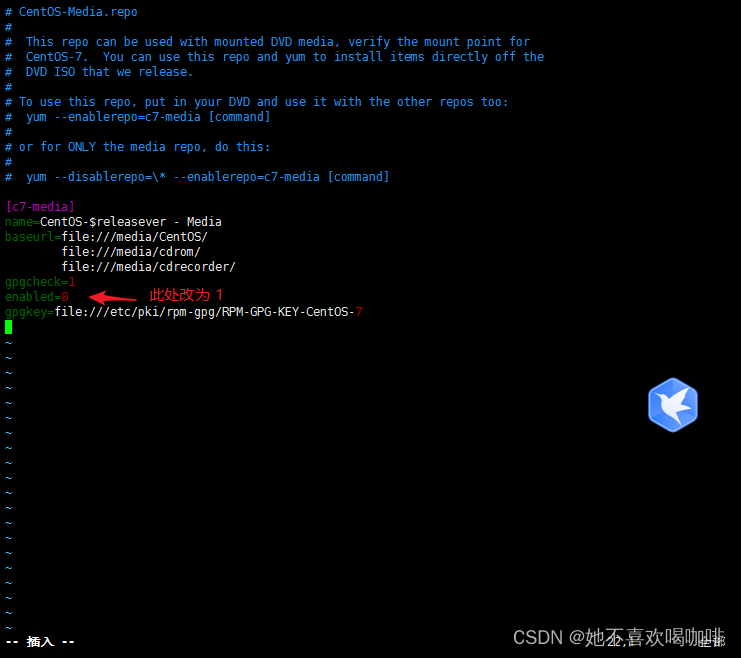
Centos 7.9 使用 iso 搭建本地 YUM 源
Centos 7.9 使用 iso 搭建本地 YUM 源 1 建立挂载点 [rootlocalhost ~]# mkdir -p /media/cdrom/ 2 创建光盘存储路径 [rootlocalhost ~]# mkdir -p /mnt/cdrom/ 3 上传 CentOS-7-x86_64-Everything-2207-02.iso 到 光盘存储路径 [rootlocalhost ~]# ls /mnt/cdrom/ CentOS-…...

NFT Insider #131:Mocaverse NFT市值破3.5万ETH,The Sandbox 参加NFCsummit
引言:NFT Insider由NFT收藏组织WHALE Members(https://twitter.com/WHALEMembers)、BeepCrypto (https://twitter.com/beep_crypto)联合出品,浓缩每周NFT新闻,为大家带来关于NFT最全面、最新鲜、…...

BatBot智慧能源管理平台,更加有效地管理能源
随着能源消耗的不断增加,能源管理已成为全球面临的重要问题。BatBot智慧能源管理作为一种的能源管理技术,促进企业在用能效率及管理有着巨大的提升。 BatBot智慧能源管理是一种基于人工智能技术的能源管理系统,通过智能分析和优化能源使用&…...

医院预约挂号系统微信小程序APP
医院预约挂号小程序,前端后台(后台 java spring boot mysql) 医院预约挂号系统具体功能介绍:展示医院信息、可以注册和登录, 预约挂号(包含各个科室的预约,可以预约每个各个医生)&…...

【代码随想录 二叉树】二叉树前序、中序、后序遍历的迭代遍历
文章目录 1. 二叉树前序遍历(迭代法)2. 二叉树后序遍历(迭代法)3. 二叉树中序遍历(迭代法) 1. 二叉树前序遍历(迭代法) 题目连接 🍎因为处理顺序和访问顺序是一致的。所…...

Error:(6, 43) java: 程序包org.springframework.data.redis.core不存在
目录 一、在做SpringBoot整合Redis的项目时,报错: 二、尝试 三、解决办法 一、在做SpringBoot整合Redis的项目时,报错: 二、尝试 给依赖加版本号,并且把版本换了个遍,也不行,也去update过ma…...
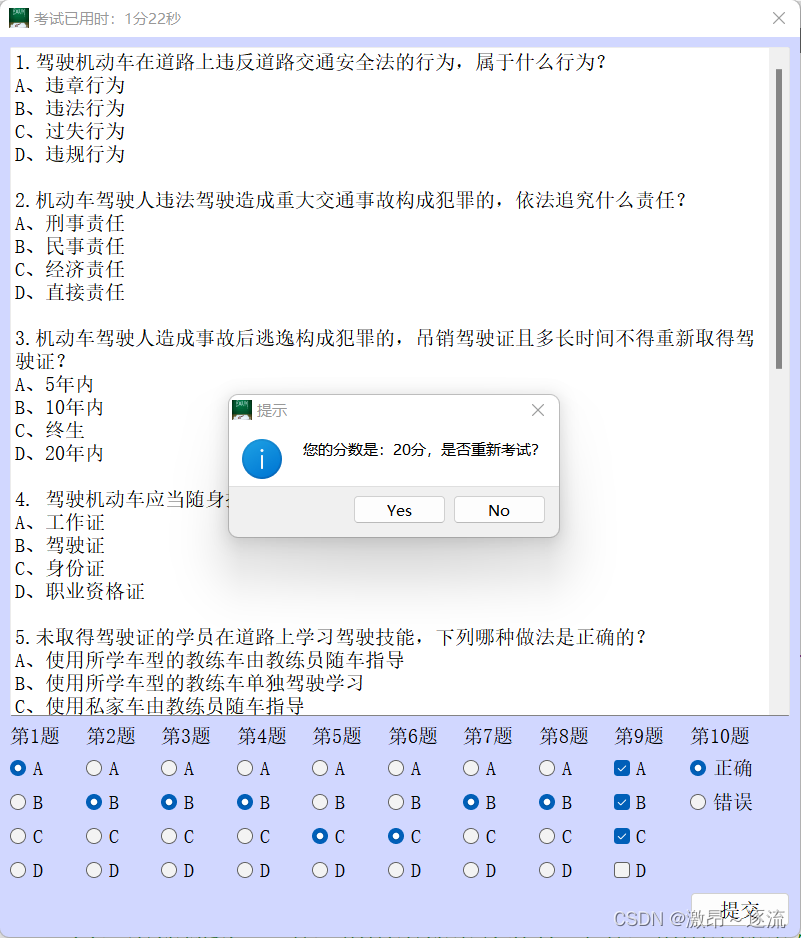
Qt 科目一考试系统(有源码)
项目源码和资源:科目一考试系统: qt实现科目一考试系统 一.项目概述 该项目是一个基于Qt框架开发的在线考试系统,主要实现了考试题目的随机抽取、考试时间限制、成绩统计等功能。用户可以通过界面操作进行考试,并查看自己的考试成绩。 二.技…...

在 Visual Studio 2022 (VS2022) 中删除 Git 分支的步骤如下
git branch -r PS \MauiApp1> git push origin --delete “20240523备份” git push origin --delete “20240523备份”...

玩转OpenHarmony智能家居:如何实现开发版“碰一碰”设备控制
一、简介 “碰一碰”设备控制,依托NFC短距通信协议,通过碰一碰的交互方式,将OpenAtom OpenHarmony(简称“OpenHarmony”)标准系统设备和全场景设备连接起来,解决了应用与设备之间接续慢、传输难的问题&…...

订餐系统总结、
应用层: SpringBoot:快速构建Spring项目,采用“约定大于配置”的思想,简化Spring项目的配置开发。 SpringMvc:Spring框架的一个模块,springmvc和spring无需通过中间整合层进行整合,可以无缝集成。 Sprin…...

【因果推断从入门到精通二】随机实验3
目录 检验无因果效应假说 硬币投掷的特殊性何在? 检验无因果效应假说 无因果效应假说认为,有些人存活,有些人死亡,但接受mAb114治疗而不是ZMapp与此无关。在174例接受mAb14治疗的患者中,113/17464.9%存活了28天&…...
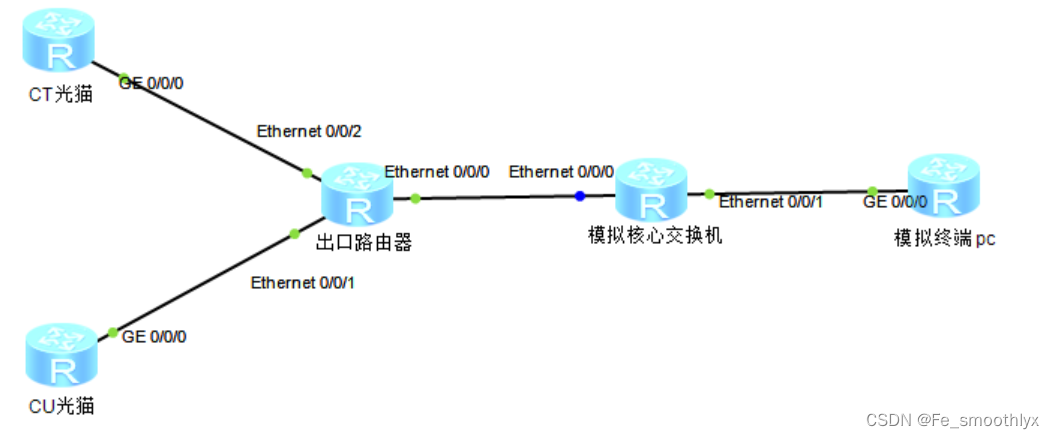
真实案例分享,终端pc直接telnet不到出口路由器。
1、背景信息 我终端pc的网卡地址获取的网关是在核心交换机上,在核心交换机上telnet出口路由器可以实现。 所有终端网段都不能telnet出口路由器,客户希望能用最小的影响方式进行解决。 2、现有配置信息 终端的无线和有线分别在两个网段中,…...

YOLOv8_seg的训练、验证、预测及导出[实例分割实践篇]
实例分割数据集链接,还是和目标检测篇一样,从coco2017val数据集中挑出来person和surfboard两类:链接:百度网盘 请输入提取码 提取码:3xmm 1.实例分割数据划分及配置 1.1实例分割数据划分 从上面得到的数据还不能够直接训练,需要按照一定的比例划分训练集和验证集,并按…...

Linux基础(四):Linux系统文件类型与文件权限
各位看官,好久不见,在正式介绍Linux的基本命令之前,我们首先了解一下,关于文件的知识。 目录 一、文件类型 二、文件权限 2.1 文件访问者的分类 2.2 文件权限 2.2.1 文件的基本权限 2.2.2 文件权限值的表示方法 三、修改文…...

本是梦中人,常作花下客。心中自往来,知我有几个。
我们总是喜欢拿“顺其自然”来敷衍人生道路上的荆棘坎坷,却很少承认,真正的顺其自然, 其实是竭尽所能之后的不强求, 而非两手一摊的不作为。 一花凋零荒芜不了整个春天, 一次挫折也荒废不了整个人生。 多年后&#x…...

创新指南|利用电商产品视频进行渠道营销的最佳策略,不断提升销售额
无论企业的利基市场如何,电商产品视频都已被证明是非常可靠的资产,可以让目标受众了解您所提供的产品——关键功能、展示重要的差异化优势甚至改变大多数营销活动的游戏规则。阅读本文,全面了解电商产品视频如何融入营销推广,以最…...
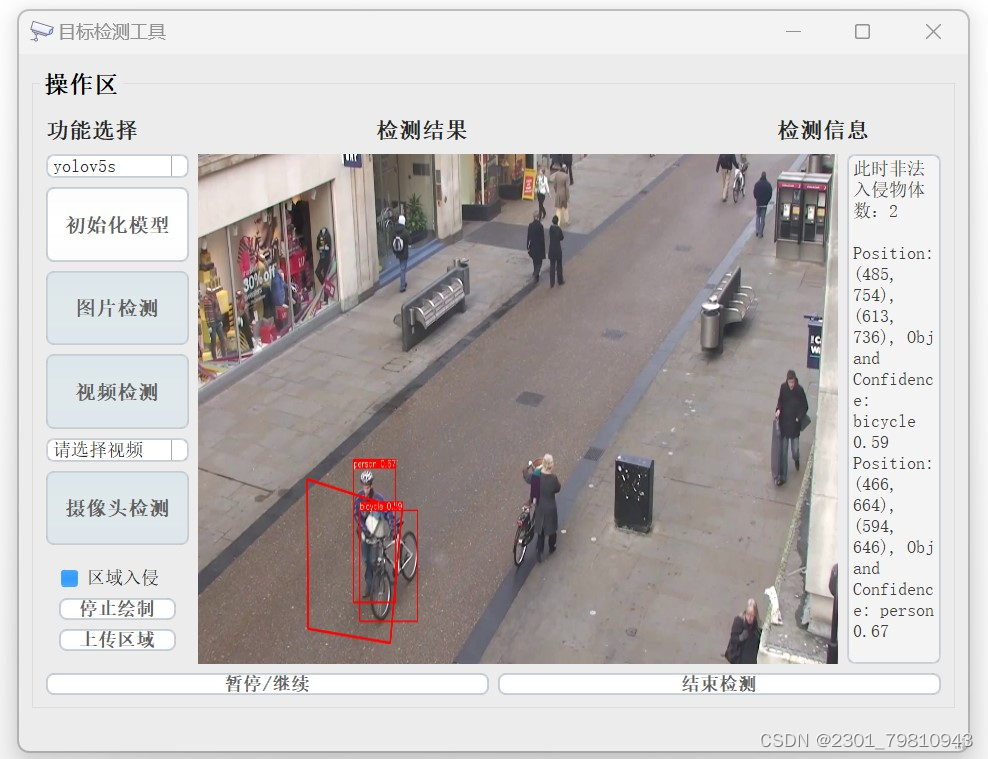
深度学习之基于YoloV5入侵检测系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景 随着信息技术的飞速发展,网络安全问题日益凸显。入侵检测系统(IDS࿰…...
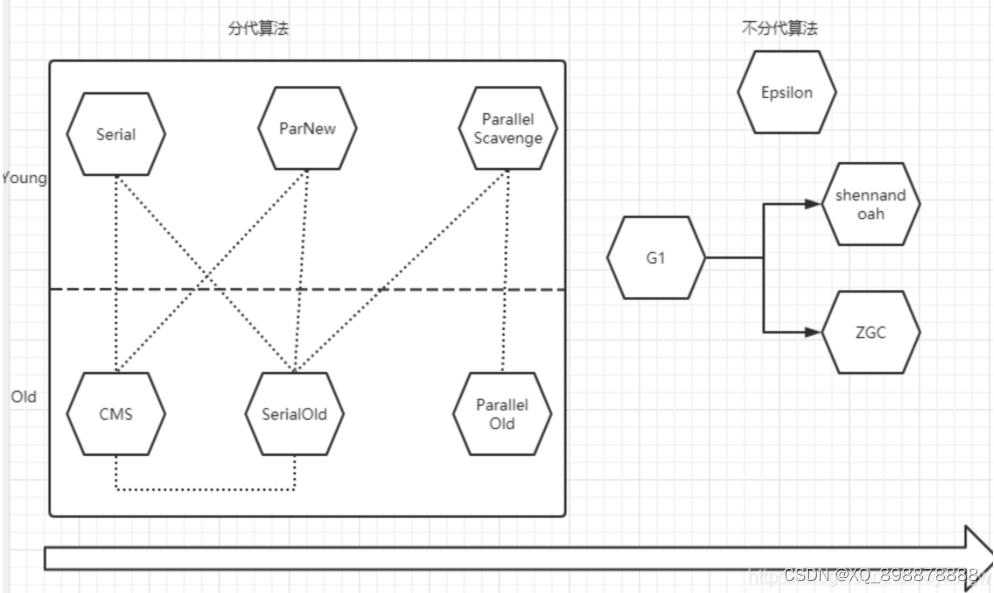
【01】全面理解JVM虚拟机
一、前言 学习JVM是进行JVM调优的基础。写的代码部署到线上它会如何运行?要配多少内存?线上环境出问题了,服务崩溃了,应该怎么快速定位?这些问题都与JVM有着一定的关系。好的程序员都应该尽自己的能力把JVM每个底层逻…...
CentOS7离线安装Nginx
目录 1. 安装gcc2. 安装g3. 安装openssl4. 安装pcre5. 安装zlib6. 安装Nginx7. 启动nginx8. 开放80端口9. 访问测试10. 设置开机自启 Nginx离线安装需要依赖gcc、g环境,安装前要先检查linux系统中是否自带gcc和g,如果没有就需要先进行安装。 然后再安装o…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
