【杂七杂八】Huawei Gt runner手表系统降级
文章目录
- Step1：下载安装修改版华为运动与健康
- Step2：在APP里进行配置
- Step3：更新固件(时间会很长)
目前在使用用鸿蒙4 111版本的手表系统，但是感觉睡眠检测和运动心率检测一言难尽，于是想到是否能回退到以前的版本？
在酷安找了一些资料，最终回退成功【免费】
Step1：下载安装修改版华为运动与健康
下载并安装华为运动健康修改Xposed模块，原帖来自wwlwwl大佬：介绍及下载链接
这个软件不仅仅可以降级，还可以安装表盘、去除华为运动健康APP的广告，还能用那个手记APP
Step2：在APP里进行配置
找到华为运动与健康中的设置，上面有一个蓝色的可以点击的地方，在里面填固件下载地址，我是华为Gtr，所有就填了这个地址：
已添加第三方加速服务https://mirror.ghproxy.com/https://github.com/cnoim/run_b29_package_2_1_0_227/releases/download/
参考图：
其他手表系列更新固件可以参考这个帖子：
华为其他手表更新固件汇总，来源cnoim
Step3：更新固件(时间会很长)
刷机有风险，祝大家一次成功！
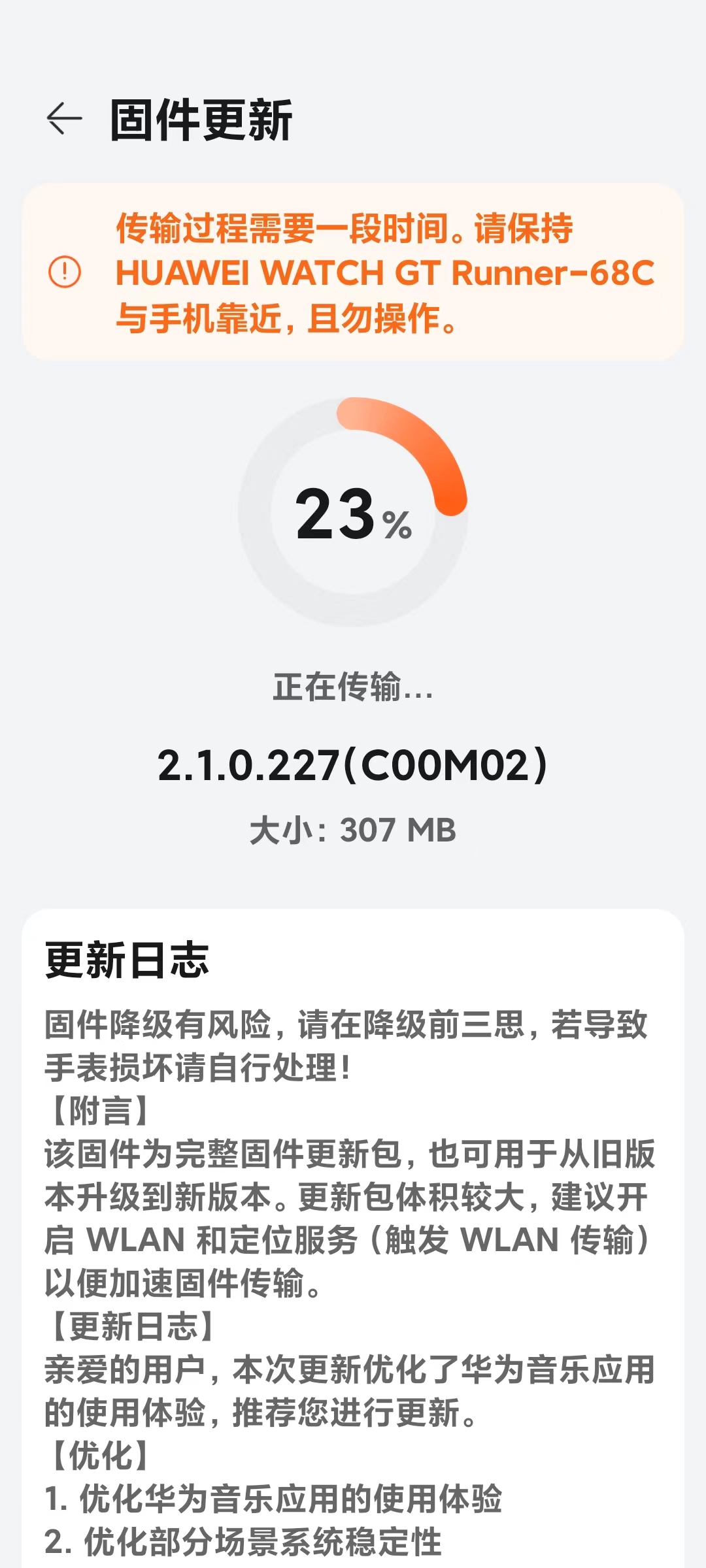
网上比较推荐 103的版本，华为手表有个比较坑的地方就是，更新要一级一级的更，我先看看出厂版本能不能用，体验几天运动和健康的检测准不准，要是准就不更新了。
相关文章：
【杂七杂八】Huawei Gt runner手表系统降级
文章目录 Step1：下载安装修改版华为运动与健康Step2：在APP里进行配置Step3：更新固件(时间会很长) 目前在使用用鸿蒙4 111版本的手表系统，但是感觉睡眠检测和运动心率检测一言难尽，于是想到是否能回退到以前的版本&…...
FMEA做不出来的原因究竟是什么？——FMEA软件
免费试用FMEA软件-免费版-SunFMEA FMEA（Failure Mode and Effects Analysis）即故障模式与影响分析，是一种旨在识别并预防潜在问题的方法。然而，尽管其重要性被广泛认知，但在实际应用中，却常常遇到FMEA难以…...
pandas ExcelWriter写excel报错openpyxl.utils.exceptions.IllegalCharacterError
一直使用pandas写excel，本次写的数据有大字段，每次写到该字段就报错，代码如下： with pd.ExcelWriter(r".\提数_20240523\tq_type3_doc.xlsx", engineopenpyxl) as writer: df.to_excel(writer,indexFalse, sheet_namesh…...
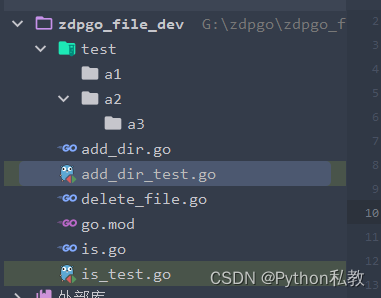
Golang创建文件夹
方法 package zdpgo_fileimport ("os" )// AddDir 创建文件夹 func AddDir(dir string) error {if !IsExist(dir) {return os.MkdirAll(dir, os.ModePerm)}return nil }测试 package zdpgo_fileimport "testing"func TestAddDir(t *testing.T) {data : […...
头歌OpenGauss数据库-I.复杂查询第5关：至少学了某位学生（Oliver）所学的全部课程的学生
本关任务：根据提供的表和数据，查询至少学了Oliver同学所学的全部课程的其他同学的信息（学号s_id，姓名`s_name）。 student表数据： s_ids_names_sex01Mia女02Riley男03Aria女04Lucas女05Oliver男06Caden男07Lily女08Jacob男course表数据： c_idc_namet_id01Chinese0202Math…...
【数据结构】哈夫曼树和哈夫曼编码
一、哈夫曼树 1.1 哈夫曼树的概念 给定一个序列，将序列中的所有元素作为叶子节点构建一棵二叉树，并使这棵树的带权路径长度最小，那么我们就得到了一棵哈夫曼树（又称最优二叉树） 接下来是名词解释： 权&a…...
深入探索微软Edge：领略新一代浏览器的无限可能
深入探索微软Edge：领略新一代浏览器的无限可能 在当今数字化时代，网络浏览器已经成为我们日常生活中不可或缺的一部分。而随着技术的不断进步，浏览器的功能和性能也在不断提升。微软Edge作为微软推出的全新一代浏览器，引领着浏览…...
JavaScript表达式和运算符
表达式 表达式一般由常量、变量、运算符、子表达式构成。最简单的表达式可以是一个简单的值。常量或变量。例：var a10 运算符 运算符一般用符号来表示，也有些使用关键字表示。运算符由3中类型 1.一元运算符：一个运算符能够结合一个操作数&…...
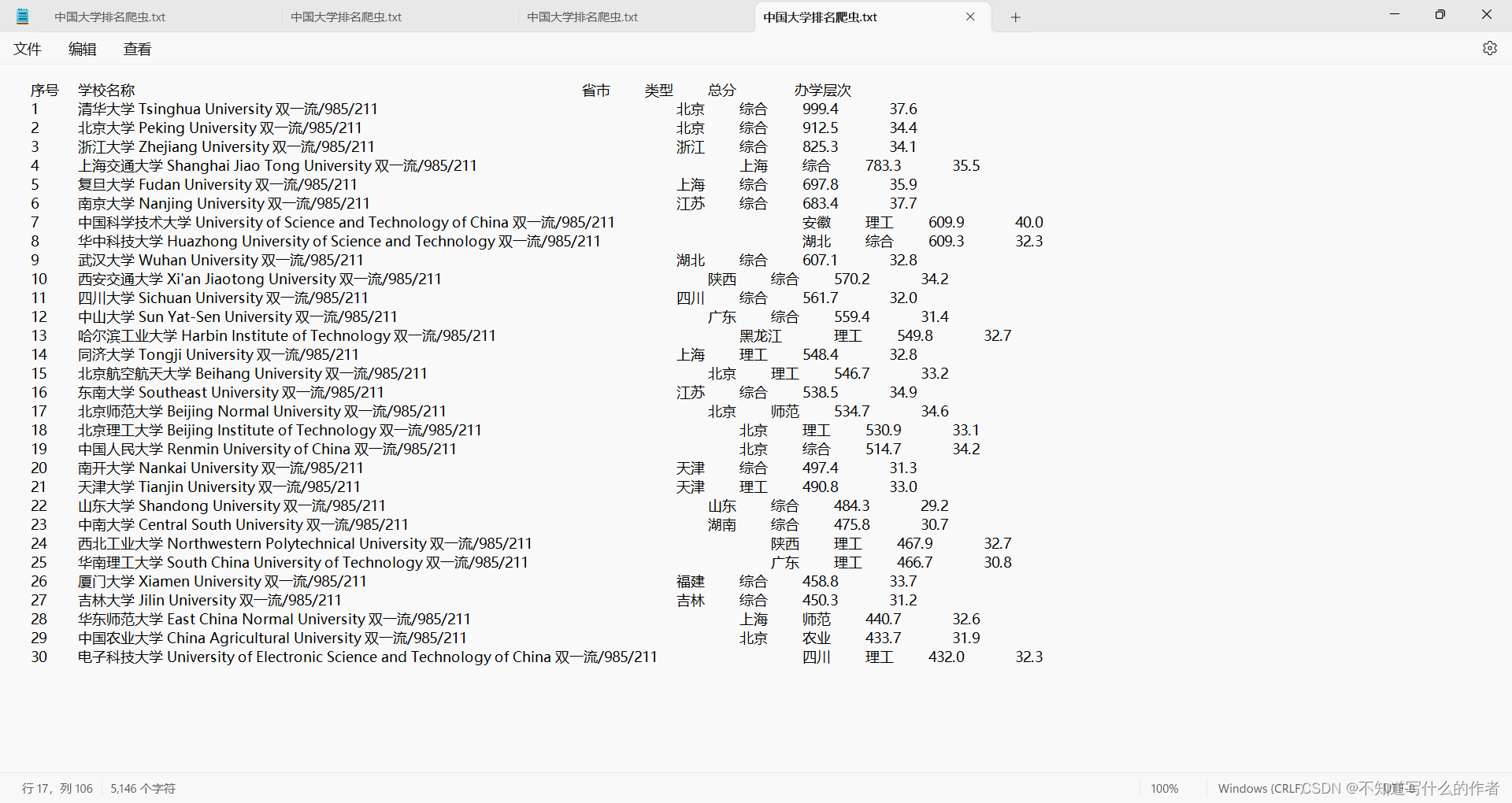
爬虫实训案例：中国大学排名
近一个月左右的时间学习爬虫，在用所积累的知识爬取了《中国大学排名》这个网站，爬取的内容虽然只是可见的文本，但对于初学者来说是一个很好的练习。在爬取的过程中，通过请求数据、解析内容、提取文本、存储数据等几个重要的内容入…...
C++ IO流
C标准IO流 使用cout进行标准输出，即数据从内存流向控制台(显示器)使用cin进行标准输入，即数据通过键盘输入到程序中使用cerr进行标准错误的输出使用clog进行日志的输出 C文件IO流 文件流对象 ofstream：只写 ofstream 是 C 中用于输出文件…...
debian nginx upsync consul 实现动态负载
1. consul 安装 wget -O- https://apt.releases.hashicorp.com/gpg | sudo gpg --dearmor -o /usr/share/keyrings/hashicorp-archive-keyring.gpg echo "deb [signed-by/usr/share/keyrings/hashicorp-archive-keyring.gpg] https://apt.releases.hashicorp.com $(lsb_r…...
前端基础入门三大核心之HTML篇 —— 同源策略的深度解析与安全实践
前端基础入门三大核心之HTML篇 —— 同源策略的深度解析与安全实践 一、同源策略：定义与起源1.1 定义浅析1.2 何为“源”？1.3 起源与意义 二、同源策略的运作机制2.1 限制范围2.2 安全边界 三、跨越同源的挑战与对策3.1 JSONP3.2 CORS3.3 postMessage 四…...
go 微服务框架 kratos 日志库使用方法及原理探究
一、Kratos 日志设计理念 kratos 日志库相关的官方文档：日志 | Kratos Kratos的日志库主要有如下特性： Logger用于对接各种日志库或日志平台，可以用现成的或者自己实现Helper是在您的项目代码中实际需要调用的，用于在业务代码里…...
VC++位移操作＞＞和＜＜以及逻辑驱动器插拔产生的掩码dbv.dbcv_unitmask进行分析的相关代码
VC位移操作>>和<<以及逻辑驱动器插拔产生的掩码dbv.dbcv_unitmask进行分析的相关代码 一、VC位移操作符<<和>>1、右位移操作符 >>：2、左位移操作符 <<： 二、逻辑驱动器插拔产生的掩码 dbv.dbcv_unitmask 进行分析的…...
查看gpu
## 查看gpu信息 if_cuda torch.cuda.is_available() print("if_cuda",if_cuda)gpu_count torch.cuda.device_count() print("gpu_count",gpu_count)...
CSS与表格设计
在网页设计中，表格是一种不可或缺的元素，用于展示和组织数据。虽然HTML提供了基本的表格结构，但通过CSS（层叠样式表）的应用，我们可以极大地提升表格的外观和用户体验。本文将探讨如何利用CSS来设计既美观又…...
阴影映射（线段树）
实时阴影是电子游戏中最为重要的画面效果之一。在计算机图形学中，通常使用阴影映射方法来实现实时阴影。 游戏开发部正在开发一款 2D 游戏，同时希望能够在 2D 游戏中模仿 3D 游戏的光影效果，请帮帮游戏开发部！ 给定 x-y 平面上的…...
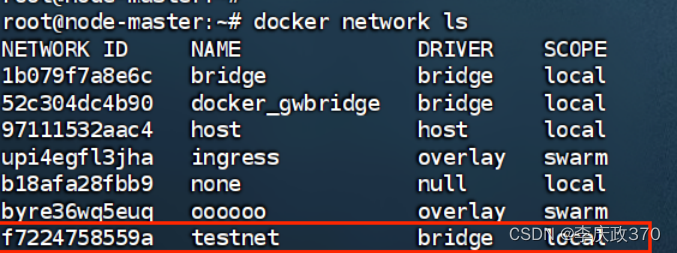
Docker 容器间通讯
1、虚拟ip/访问 同一网络 安装docker时，docker会默认创建一个内部的桥接网络docker0，每创建一个容器分配一个虚拟网卡，容器之间(包括宿主机)可以根据分配的ip互相访问(ps:其他主机(包括其他主机的容器)无法ping通docker容器ip无法访问&#…...
C语言章节学习归纳--数据类型、运算符与表达式
3.1 C语言的数据类型（理解） 首先，对变量的定义可以包括三个方面： 数据类型 存储类型 作用域 所谓数据类型是按被定义变量的性质，表示形式，占据存储空间的多少，构造特点来划分的。在C语言中&…...
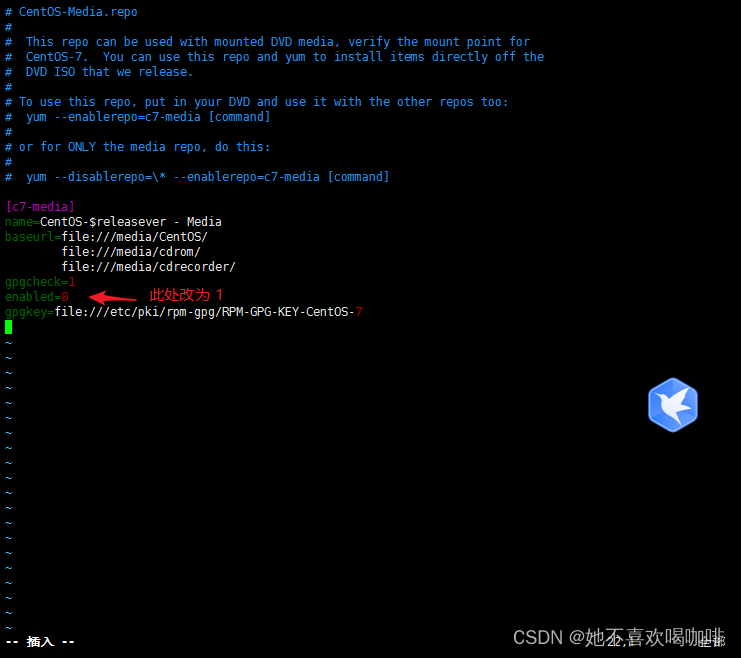
Centos 7.9 使用 iso 搭建本地 YUM 源
Centos 7.9 使用 iso 搭建本地 YUM 源 1 建立挂载点 [rootlocalhost ~]# mkdir -p /media/cdrom/ 2 创建光盘存储路径 [rootlocalhost ~]# mkdir -p /mnt/cdrom/ 3 上传 CentOS-7-x86_64-Everything-2207-02.iso 到 光盘存储路径 [rootlocalhost ~]# ls /mnt/cdrom/ CentOS-…...
Phi-3-mini-4k-instruct-gguf辅助前端开发：基于VSCode的智能代码补全实践
Phi-3-mini-4k-instruct-gguf辅助前端开发：基于VSCode的智能代码补全实践 1. 引言：当AI遇见前端开发 最近在写前端代码时，我经常遇到这样的情况：明明知道要实现什么功能，却卡在具体语法细节上；或者反复写…...
网络安全培训资源awesome-osint：OSINT视频教程与博客指南
网络安全培训资源awesome-osint：OSINT视频教程与博客指南 开源情报（OSINT）是网络安全领域的重要技能，通过公开可用的信息源收集情报。对于网络安全新手和从业者来说，找到高质量的OSINT培训资源至关重要。awesome-osin…...
BetterJoy解决Switch手柄PC适配难题：高效无缝的全场景控制器解决方案
BetterJoy解决Switch手柄PC适配难题：高效无缝的全场景控制器解决方案 【免费下载链接】BetterJoy Allows the Nintendo Switch Pro Controller, Joycons and SNES controller to be used with CEMU, Citra, Dolphin, Yuzu and as generic XInput 项目地址: https:…...
打破语言壁垒：GitHub全界面本地化实践指南
打破语言壁垒：GitHub全界面本地化实践指南 【免费下载链接】github-chinese GitHub 汉化插件，GitHub 中文化界面。 (GitHub Translation To Chinese) 项目地址: https://gitcode.com/gh_mirrors/gi/github-chinese 作为全球最大的代码托管平台&am…...
如何判断便宜的SEO优化公司是否靠谱_如何在保证质量的前提下找到便宜的SEO优化
如何判断便宜的SEO优化公司是否靠谱_如何在保证质量的前提下找到便宜的SEO优化 在当今竞争激烈的商业环境中，搜索引擎优化（SEO）已经成为提高网站流量和品牌知名度的关键手段。随着越来越多的公司进入SEO市场，如何判断便宜的SEO优…...
论文答辩智能化：10款AI辅助工具推荐（附爱毕业aibiye使用技巧）
工具对比速览表 工具名称 核心功能 适用场景 特色优势 Aibiye 智能成文、文献查找、数据分析 社科/金融/理工类论文 融合多模型架构，精准把握高校规范 Aicheck 初稿生成、大纲定制、图表插入 快速完成初稿需求 全学科覆盖，20-30分钟极速生成 …...
Wan2.1视频生成创意玩法：把你的想法变成动态视觉故事
Wan2.1视频生成创意玩法：把你的想法变成动态视觉故事 1. 从文字到视频的魔法 你有没有过这样的经历？脑海中浮现出一个绝妙的创意场景，却苦于没有专业的视频制作技能将它呈现出来。或许是一个科幻故事的开场，一个产品演示的构想&…...
RCS 核心系统架构：AGV 调度“大脑”的底层逻辑
在现代智能物流与制造系统中，RCS（Robot Control System）作为 AGV 集群的核心调度中枢，扮演着"智慧大脑"的关键角色。不同于单台 AGV 的自主导航，RCS 需要解决多车协同、任务分配、路径规划与冲突避免等复杂问…...
测试流程图显示
一、原理解析 / 概念介绍 1.1 自动化序列化流水线 hive_generator 处于开发链路的“后台”，负责将 Dart 对象转换为 Hive 识别的二进制流编码逻辑。 #mermaid-svg-bbx9YEu5DFSBhCuG{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;…...
SecGPT-14B模型微调：提升OpenClaw安全任务执行准确率
SecGPT-14B模型微调：提升OpenClaw安全任务执行准确率 1. 为什么需要微调SecGPT-14B 去年我在使用OpenClaw自动化执行安全扫描任务时，经常遇到一个头疼的问题：当Agent尝试分析漏洞报告时，基础模型总是把"SSRF漏洞"和&q…...