【数据结构】哈夫曼树和哈夫曼编码
一、哈夫曼树
1.1 哈夫曼树的概念
给定一个序列,将序列中的所有元素作为叶子节点构建一棵二叉树,并使这棵树的带权路径长度最小,那么我们就得到了一棵哈夫曼树(又称最优二叉树)
接下来是名词解释:
- 权:节点的数值
- 路径长度:两节点间路径的边数
- 带权路径长度:节点的权值乘以该节点到根节点的路径长度即为该节点的带权路径长度。哈夫曼树的带权路径长度是树中所有叶子节点的带权路径长度之和。
例如下面这棵哈夫曼树:

通过观察我们可以发现,所有父节点的权值都是自身的两个子节点的权值之和。而为了要使树的带权路径长度最小,我们要尽可能的让权值小的节点离根节点远,让权值大的节点离根节点近。
因此,我们引出哈夫曼树的构造算法。
1.2 哈夫曼树的构造算法
要将一个序列构造成一棵哈夫曼树,我们首先需要对其进行升序排序

将排序好后的序列中的每个值看作一棵只有一个节点的树,从中选出根节点权值最小的两棵树作为新树的左右子树,并将这两棵树从序列中删除,而新树的根节点的权值是这两棵树根节点的权值之和
哈夫曼树没有规定左右子树的顺序,因此下面的例子中将10和18的位置对调也是正确的
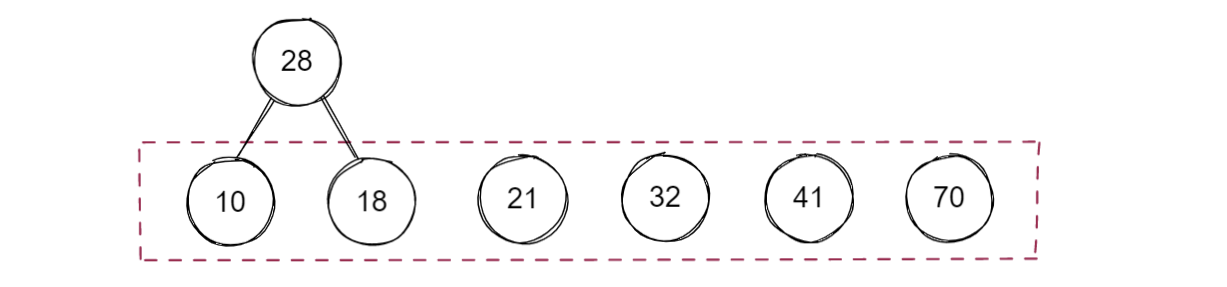
将新树的根节点的权值放入序列中并重新进行升序排序,重复上述步骤
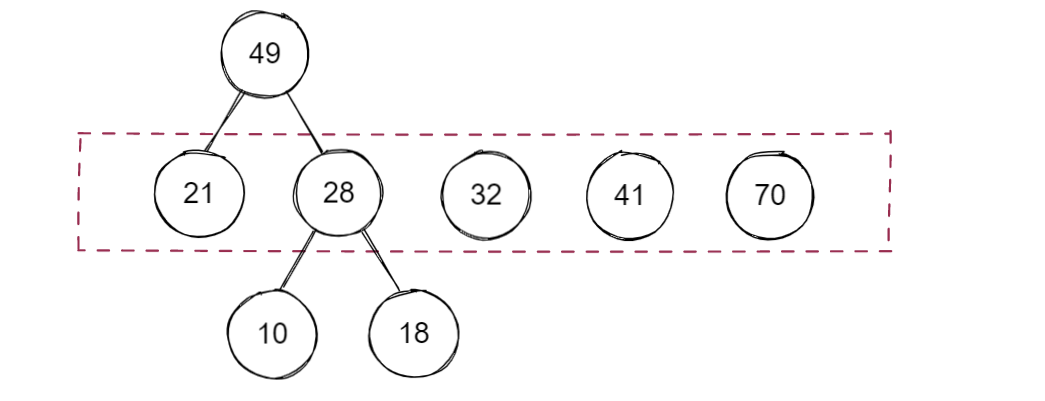


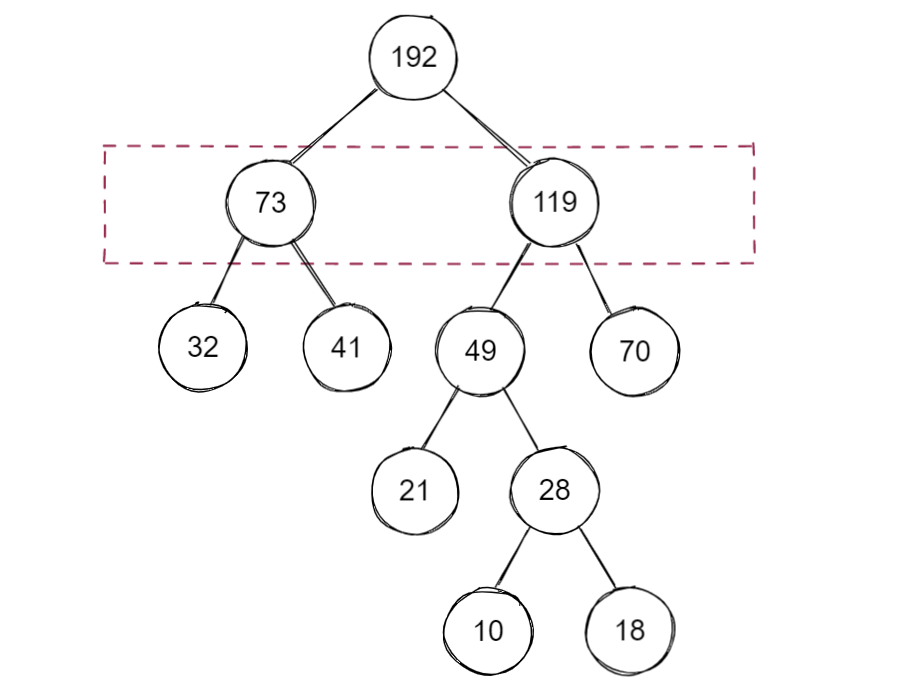
至此,就构建了一棵哈夫曼树
因为哈夫曼树没有规定左右子树的顺序,因此一个序列可以构建出不同的哈夫曼树
二、哈夫曼编码
2.1 等长编码
假设我们要对一个字符串ABAACDC进行二进制编码
我们可以按顺序给每个字符设置一个编码,A为0,B为1,C为10,D为11
那么就可以将上面的字符串转化为0100101110
但是在解码的时候我们会发现,这一串二进制序列可以解码为ACACDBA、ACABABDA等字符串,出现了歧义。
这是因为我们在对字符进行编码的时候,出现了一个字符是另一个字符的前缀的情况,例如D可以用两个B来表示。
为了避免歧义,我们可以采用等长编码的方案,就是每个字符的编码都一样长,例如A为00,B为01,C为10,D为11,这样就不会产生歧义了。
但是这种方案并不是一个最短的方案。
2.2 哈夫曼编码
统计字符出现的次数,把字符定义成一个节点,节点的权值就是它出现的次数。
例如上面A出现了3次,B出现了1次,C出现了2次,D出现了1次
哈夫曼编码的核心思想就是让出现次数越多的字符编出来的码越短,我们将全部节点构建成一棵哈夫曼树,出现次数越少的字符对应的节点就越靠近树的底层,编码也就越长,出现次数越多的字符编码就越短。
对二叉树的边标号,向左的边标为0,向右的边标为1,至此所有字符的编码就是从根节点到该字符节点路径上经过的标号,例如A为1,B为010,C为00,D为011,这种编码方案就叫做哈夫曼编码。

构建哈夫曼树的时候,所有的字符节点都是叶子节点,不会出现一个字符出现在另一个字符的路径上,也就不会出现一个字符是另一个字符的前缀这种造成歧义的情况
哈夫曼树的编码不是唯一的,节点放置的左右也会造成字符编码的不同,但是生成的编码长度一定都是一样的。
完.
相关文章:

【数据结构】哈夫曼树和哈夫曼编码
一、哈夫曼树 1.1 哈夫曼树的概念 给定一个序列,将序列中的所有元素作为叶子节点构建一棵二叉树,并使这棵树的带权路径长度最小,那么我们就得到了一棵哈夫曼树(又称最优二叉树) 接下来是名词解释: 权&a…...

深入探索微软Edge:领略新一代浏览器的无限可能
深入探索微软Edge:领略新一代浏览器的无限可能 在当今数字化时代,网络浏览器已经成为我们日常生活中不可或缺的一部分。而随着技术的不断进步,浏览器的功能和性能也在不断提升。微软Edge作为微软推出的全新一代浏览器,引领着浏览…...

JavaScript表达式和运算符
表达式 表达式一般由常量、变量、运算符、子表达式构成。最简单的表达式可以是一个简单的值。常量或变量。例:var a10 运算符 运算符一般用符号来表示,也有些使用关键字表示。运算符由3中类型 1.一元运算符:一个运算符能够结合一个操作数&…...
爬虫实训案例:中国大学排名
近一个月左右的时间学习爬虫,在用所积累的知识爬取了《中国大学排名》这个网站,爬取的内容虽然只是可见的文本,但对于初学者来说是一个很好的练习。在爬取的过程中,通过请求数据、解析内容、提取文本、存储数据等几个重要的内容入…...

C++ IO流
C标准IO流 使用cout进行标准输出,即数据从内存流向控制台(显示器)使用cin进行标准输入,即数据通过键盘输入到程序中使用cerr进行标准错误的输出使用clog进行日志的输出 C文件IO流 文件流对象 ofstream:只写 ofstream 是 C 中用于输出文件…...

debian nginx upsync consul 实现动态负载
1. consul 安装 wget -O- https://apt.releases.hashicorp.com/gpg | sudo gpg --dearmor -o /usr/share/keyrings/hashicorp-archive-keyring.gpg echo "deb [signed-by/usr/share/keyrings/hashicorp-archive-keyring.gpg] https://apt.releases.hashicorp.com $(lsb_r…...

前端基础入门三大核心之HTML篇 —— 同源策略的深度解析与安全实践
前端基础入门三大核心之HTML篇 —— 同源策略的深度解析与安全实践 一、同源策略:定义与起源1.1 定义浅析1.2 何为“源”?1.3 起源与意义 二、同源策略的运作机制2.1 限制范围2.2 安全边界 三、跨越同源的挑战与对策3.1 JSONP3.2 CORS3.3 postMessage 四…...

go 微服务框架 kratos 日志库使用方法及原理探究
一、Kratos 日志设计理念 kratos 日志库相关的官方文档:日志 | Kratos Kratos的日志库主要有如下特性: Logger用于对接各种日志库或日志平台,可以用现成的或者自己实现Helper是在您的项目代码中实际需要调用的,用于在业务代码里…...

VC++位移操作>>和<<以及逻辑驱动器插拔产生的掩码dbv.dbcv_unitmask进行分析的相关代码
VC位移操作>>和<<以及逻辑驱动器插拔产生的掩码dbv.dbcv_unitmask进行分析的相关代码 一、VC位移操作符<<和>>1、右位移操作符 >>:2、左位移操作符 <<: 二、逻辑驱动器插拔产生的掩码 dbv.dbcv_unitmask 进行分析的…...

查看gpu
## 查看gpu信息 if_cuda torch.cuda.is_available() print("if_cuda",if_cuda)gpu_count torch.cuda.device_count() print("gpu_count",gpu_count)...

CSS与表格设计
在网页设计中,表格是一种不可或缺的元素,用于展示和组织数据。虽然HTML提供了基本的表格结构,但通过CSS(层叠样式表)的应用,我们可以极大地提升表格的外观和用户体验。本文将探讨如何利用CSS来设计既美观又…...

阴影映射(线段树)
实时阴影是电子游戏中最为重要的画面效果之一。在计算机图形学中,通常使用阴影映射方法来实现实时阴影。 游戏开发部正在开发一款 2D 游戏,同时希望能够在 2D 游戏中模仿 3D 游戏的光影效果,请帮帮游戏开发部! 给定 x-y 平面上的…...
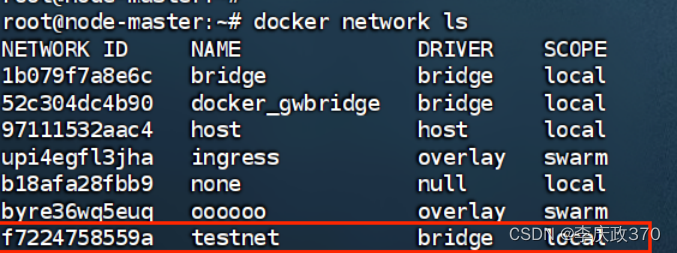
Docker 容器间通讯
1、虚拟ip/访问 同一网络 安装docker时,docker会默认创建一个内部的桥接网络docker0,每创建一个容器分配一个虚拟网卡,容器之间(包括宿主机)可以根据分配的ip互相访问(ps:其他主机(包括其他主机的容器)无法ping通docker容器ip无法访问&#…...

C语言章节学习归纳--数据类型、运算符与表达式
3.1 C语言的数据类型(理解) 首先,对变量的定义可以包括三个方面: 数据类型 存储类型 作用域 所谓数据类型是按被定义变量的性质,表示形式,占据存储空间的多少,构造特点来划分的。在C语言中&…...
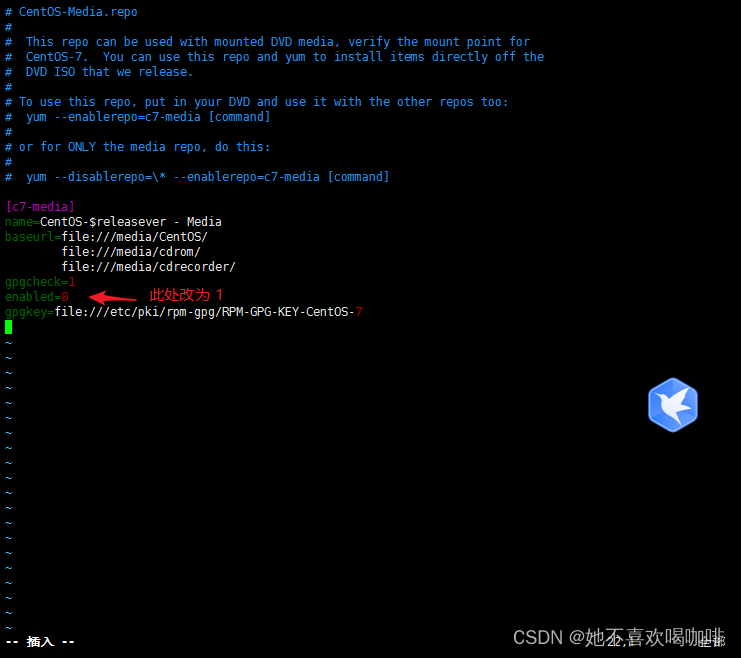
Centos 7.9 使用 iso 搭建本地 YUM 源
Centos 7.9 使用 iso 搭建本地 YUM 源 1 建立挂载点 [rootlocalhost ~]# mkdir -p /media/cdrom/ 2 创建光盘存储路径 [rootlocalhost ~]# mkdir -p /mnt/cdrom/ 3 上传 CentOS-7-x86_64-Everything-2207-02.iso 到 光盘存储路径 [rootlocalhost ~]# ls /mnt/cdrom/ CentOS-…...

NFT Insider #131:Mocaverse NFT市值破3.5万ETH,The Sandbox 参加NFCsummit
引言:NFT Insider由NFT收藏组织WHALE Members(https://twitter.com/WHALEMembers)、BeepCrypto (https://twitter.com/beep_crypto)联合出品,浓缩每周NFT新闻,为大家带来关于NFT最全面、最新鲜、…...

BatBot智慧能源管理平台,更加有效地管理能源
随着能源消耗的不断增加,能源管理已成为全球面临的重要问题。BatBot智慧能源管理作为一种的能源管理技术,促进企业在用能效率及管理有着巨大的提升。 BatBot智慧能源管理是一种基于人工智能技术的能源管理系统,通过智能分析和优化能源使用&…...

医院预约挂号系统微信小程序APP
医院预约挂号小程序,前端后台(后台 java spring boot mysql) 医院预约挂号系统具体功能介绍:展示医院信息、可以注册和登录, 预约挂号(包含各个科室的预约,可以预约每个各个医生)&…...

【代码随想录 二叉树】二叉树前序、中序、后序遍历的迭代遍历
文章目录 1. 二叉树前序遍历(迭代法)2. 二叉树后序遍历(迭代法)3. 二叉树中序遍历(迭代法) 1. 二叉树前序遍历(迭代法) 题目连接 🍎因为处理顺序和访问顺序是一致的。所…...

Error:(6, 43) java: 程序包org.springframework.data.redis.core不存在
目录 一、在做SpringBoot整合Redis的项目时,报错: 二、尝试 三、解决办法 一、在做SpringBoot整合Redis的项目时,报错: 二、尝试 给依赖加版本号,并且把版本换了个遍,也不行,也去update过ma…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
