day 38 435.无重叠区间 763.划分字母区间 56. 合并区间 738.单调递增的数字 968.监控二叉树
435.无重叠区间
思路
为了使区间尽可能的重叠所以排序来使区间尽量的重叠,使用左边界排序来统计重叠区间的个数与452. 用最少数量的箭引爆气球恰好相反。
代码
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));int count = 0;for (int i = 1; i < intervals.length; i++) {if(intervals[i-1][1] > intervals[i][0]){count++;intervals[i][1] = Math.min(intervals[i-1][1],intervals[i][1]);}}return count;}
}763.划分字母区间
思路
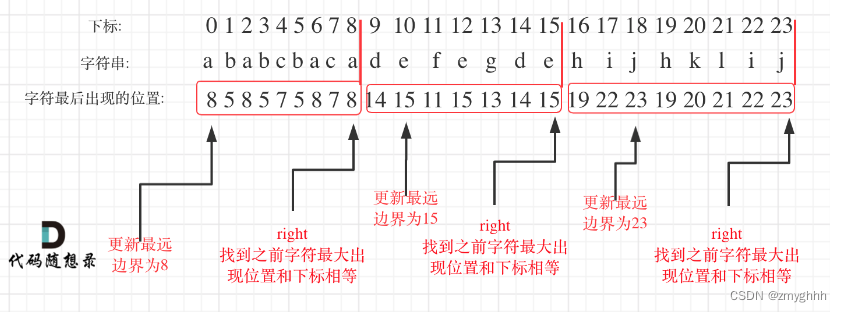
首先想到了回溯但是使用回溯依然没有思路,在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
代码
class Solution {public List<Integer> partitionLabels(String s) {List<Integer> list = new LinkedList<>();int [] hash = new int[27];char [] chars = s.toCharArray();for (int i = 0; i < chars.length; i++) {hash[chars[i] - 'a'] = i;}int left = 0,right = 0 ;for (int i = 0; i < chars.length; i++) {right = Math.max(right , hash[chars[i] - 'a']);if(i == right){list.add(right -left +1);left = i+1;}}return list;}
}56. 合并区间
思路
本题的本质其实还是判断重叠区间问题。452. 用最少数量的箭引爆气球 (opens new window)和 435. 无重叠区间都是判断区间重叠,区别就是判断区间重叠后的逻辑,本题是判断区间重贴后要进行区间合并。

代码
class Solution {public int[][] merge(int[][] intervals) {LinkedList<int[]> res = new LinkedList<>();Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));res.add(intervals[0]);for (int i = 1; i < intervals.length; i++) {if (intervals[i][0] <= res.getLast()[1]) {int start = res.getLast()[0];int end = Math.max(intervals[i][1], res.getLast()[1]);res.removeLast();res.add(new int[]{start, end});}else {res.add(intervals[i]);}}return res.toArray(new int[res.size()][]);}
}738.单调递增的数字
思路
贪心算法
例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
class Solution {public int monotoneIncreasingDigits(int n) {String s = String.valueOf(n);char[] chars = s.toCharArray();int start = s.length();for (int i = s.length() - 2; i >= 0; i--) {if (chars[i] > chars[i + 1]) {chars[i]--;start = i+1;}}for (int i = start; i < s.length(); i++) {chars[i] = '9';}return Integer.parseInt(String.valueOf(chars));}
}968.监控二叉树
思路
题目示例中的摄像头都没有放在叶子节点上!这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。
所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
为什么不从头结点开始看起呢,为啥要从叶子节点看呢?
因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。(也算是一个贪心)
局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,
整体最优:全部摄像头数量所用最少!
思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
在二叉树中如何从低向高推导呢?
可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。左孩子的返回值,右孩子的返回值,即left 和 right, 以后推导中间节点的状态
难点
每个节点可能有几种状态:
有如下三种:
- 该节点无覆盖(无摄像头)
- 本节点有摄像头
- 本节点有覆盖(无摄像头)
空节点的状态只能是有覆盖
为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
主要有如下四类情况:
- 情况1:左右节点都有覆盖
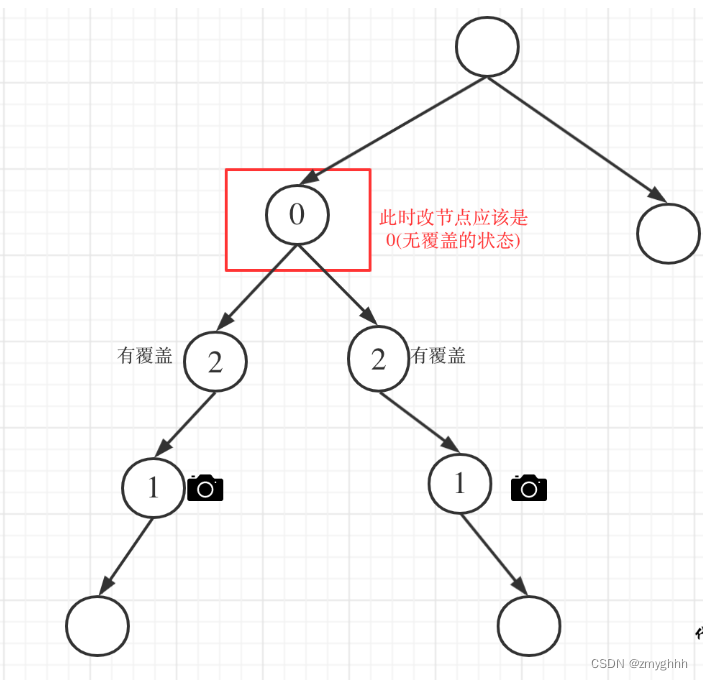
- 情况2:左右节点至少有一个无覆盖的情况:中间节点(父节点)应该放摄像头
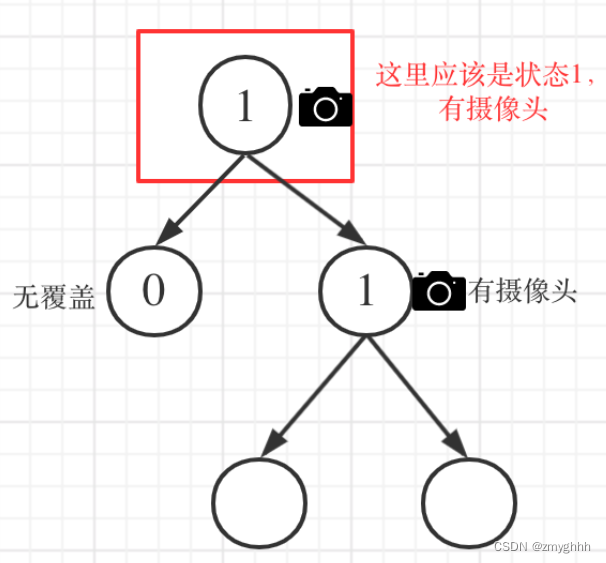
如果left == 1, right == 0 怎么办?其实这种条件在情况2中已经判断过了,如图:
- 情况3:左右节点至少有一个有摄像头:左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
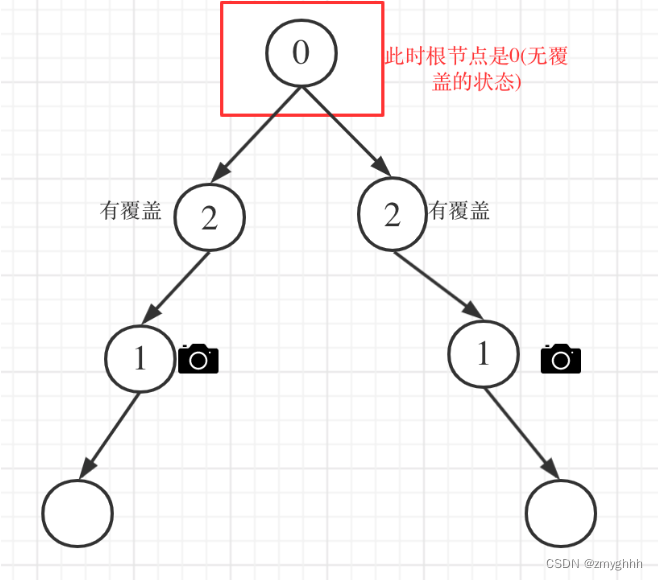
- 情况4:头结点没有覆盖
代码
class Solution {int result = 0 ;public int minCameraCover(TreeNode root) {if(traversal(root) == 0){result++;}return result;}/**节点的状态值:0 表示无覆盖1 表示 有摄像头2 表示有覆盖后序遍历,根据左右节点的情况,来判读 自己的状态*/public int traversal(TreeNode root){if(root == null) return 2;int left = traversal(root.left);int right = traversal(root.right);if(left==2 && right==2) return 0;if(left == 0 || right ==0){result++;return 1;}if(left == 1 || right ==1){return 2;}return -1;}
}相关文章:

day 38 435.无重叠区间 763.划分字母区间 56. 合并区间 738.单调递增的数字 968.监控二叉树
435.无重叠区间 思路 为了使区间尽可能的重叠所以排序来使区间尽量的重叠,使用左边界排序来统计重叠区间的个数与452. 用最少数量的箭引爆气球恰好相反。 代码 class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,…...
ssm/springoot养老院问诊服务预约系统_96316老年人服务系统
2.管理员: (1)登入注册页面:管理员进行操作时需要是已注册登入的 (2)权限管理:管理员登入后可以运用权限进行相应的操作管理。 (3)用户管理:对用户进行删除、…...

WordPress插件优化对提升性能有多大影响?
WordPress插件优化对提升性能的影响可以是非常显著的。插件是WordPress平台的一个重要组成部分,它们可以增强网站的功能和定制性。然而,如果插件没有经过优化,它们可能会成为网站性能的瓶颈。 通过优化插件,可以减少对服务器资源…...
Servlet的response对象
目录 HTTP响应报文协议 reponse继承体系 reponse的方法 响应行 public void setStatus(int sc) 响应头 public void setHeader(String name, String value) 响应体 public java.io.PrintWriter getWriter() public ServletOutputStream getOutputStream() 请求重定…...

Unity射击游戏开发教程:(20)增加护盾强度
在本文中,我们将增强护盾,使其在受到超过 1 次攻击后才会被禁用。 Player 脚本具有 Shield PowerUp 方法,我们需要调整盾牌在被摧毁之前可以承受的数量,因此我们将声明一个 int 变量来设置盾牌可以承受的击中数量。...

初识C语言——第二十八天
代码练习1: 用函数的方式实现9*9乘法表 void print_table(int n) {int i 0;int j 0;for (i 1; i< n; i){for (j 1; j< i; j){printf("%d*%d%-3d ", i, j, i * j);}printf("\n");}}int main() {int n 0;scanf("%d", &a…...
输入事件分发到Native层的流程)
Android NDK系列(三)输入事件分发到Native层的流程
在Android NDK系列(一)手动搭建Native Project 创建的Native工程中,是可以接收输入事件的,只需在android_main中注册输入事件的处理函数,当触摸屏幕后,handleInputEvent函数便会调用,代码如下。 static int32_t handleInputEvent(struct android_app* app, AInputEvent…...
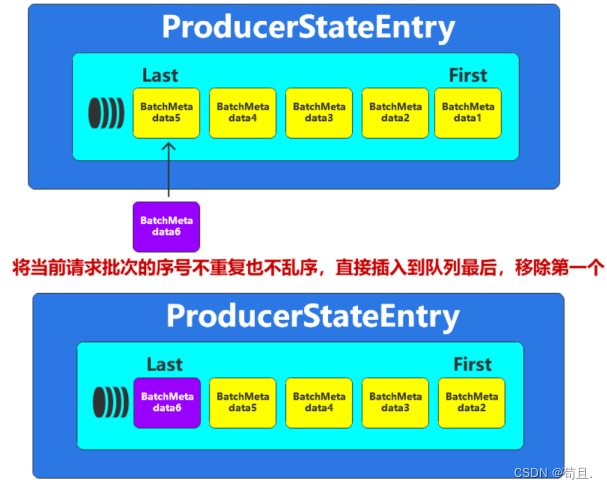
Kafka之【生产消息】
消息(Record) 在kafka中传递的数据我们称之为消息(message)或记录(record),所以Kafka发送数据前,需要将待发送的数据封装为指定的数据模型: 相关属性必须在构建数据模型时指定,其中…...
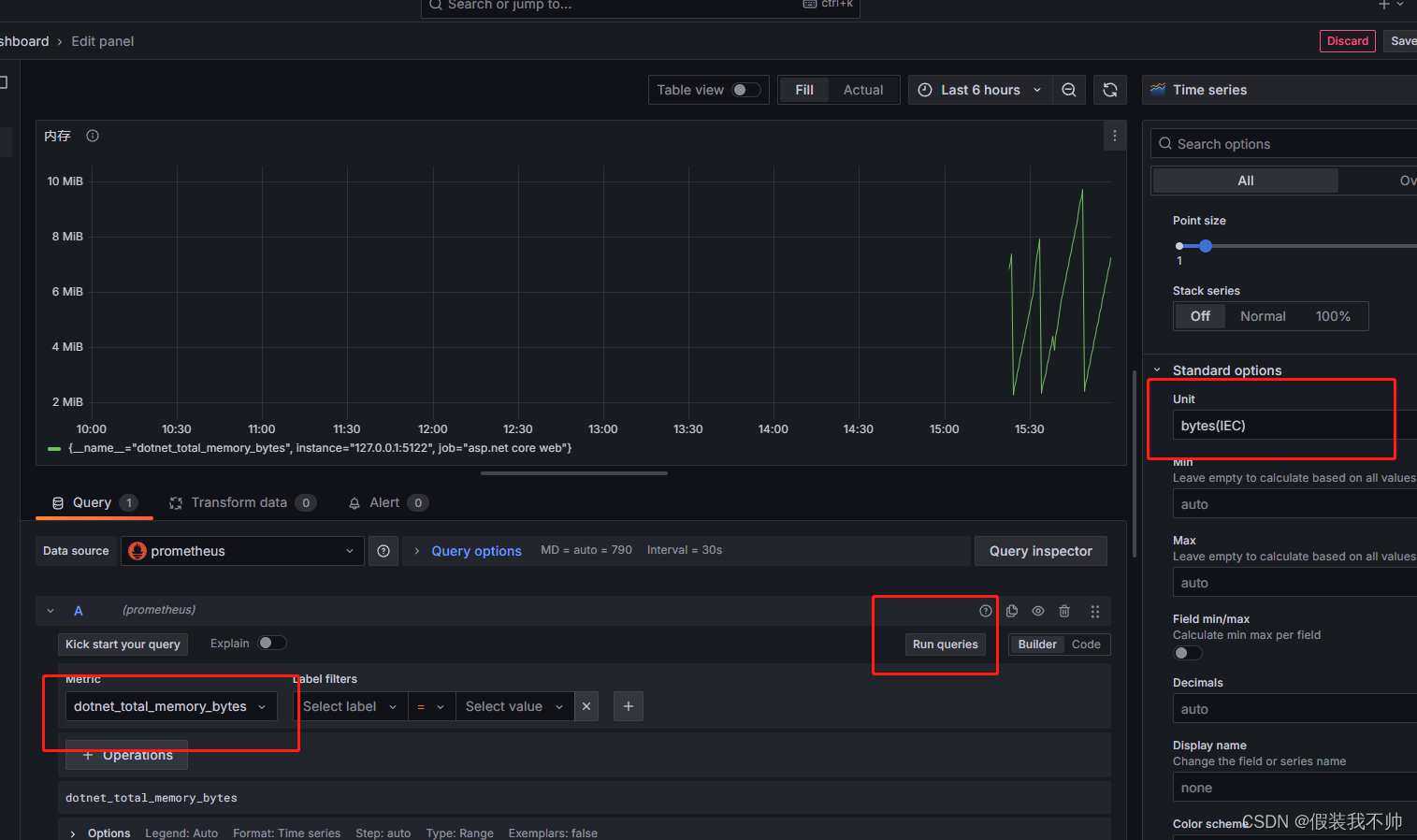
asp.net core接入prometheus
安装prometheus和Grafana 参考之前的文章->安装prometheus和Grafana教程 源代码 dotnet源代码 新建.net core7 web项目 修改Program.cs using Prometheus;namespace PrometheusStu01;public class Program {public static void Main(string[] args){var builder We…...

C++ 变量类型与转换
C 变量类型与转换 文章目录 C 变量类型与转换变量int_tsize_t与ssize_tpid_ttime_t typenametypeid关键字类型转换编译期类型转换std::static_cast注意事项运行时类型转换std::dynamic_cast 变量 int_t 它是通过typedef定义的,而不是一种新的数据类型。 - int8_t…...
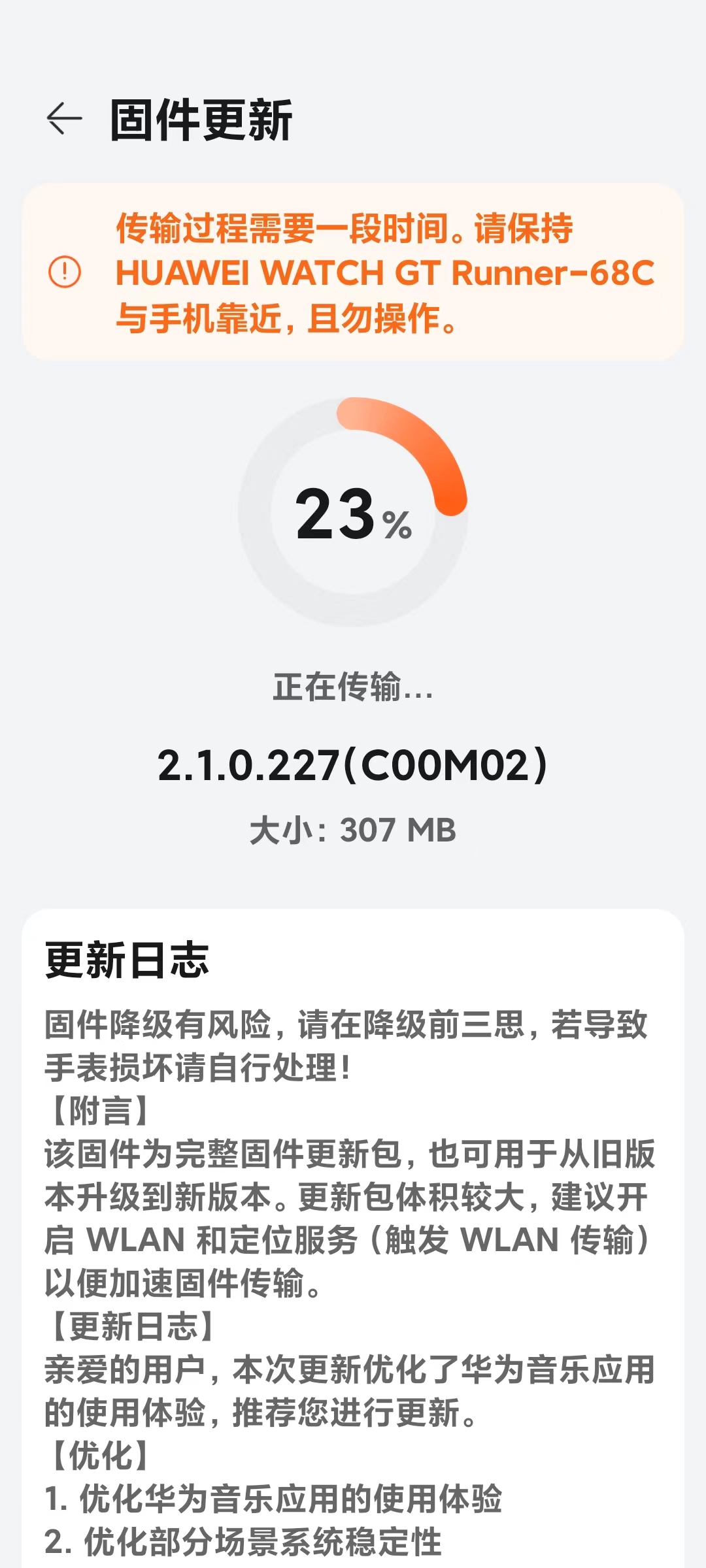
【杂七杂八】Huawei Gt runner手表系统降级
文章目录 Step1:下载安装修改版华为运动与健康Step2:在APP里进行配置Step3:更新固件(时间会很长) 目前在使用用鸿蒙4 111版本的手表系统,但是感觉睡眠检测和运动心率检测一言难尽,于是想到是否能回退到以前的版本&…...

FMEA做不出来的原因究竟是什么?——FMEA软件
免费试用FMEA软件-免费版-SunFMEA FMEA(Failure Mode and Effects Analysis)即故障模式与影响分析,是一种旨在识别并预防潜在问题的方法。然而,尽管其重要性被广泛认知,但在实际应用中,却常常遇到FMEA难以…...

pandas ExcelWriter写excel报错openpyxl.utils.exceptions.IllegalCharacterError
一直使用pandas写excel,本次写的数据有大字段,每次写到该字段就报错,代码如下: with pd.ExcelWriter(r".\提数_20240523\tq_type3_doc.xlsx", engineopenpyxl) as writer: df.to_excel(writer,indexFalse, sheet_namesh…...
Golang创建文件夹
方法 package zdpgo_fileimport ("os" )// AddDir 创建文件夹 func AddDir(dir string) error {if !IsExist(dir) {return os.MkdirAll(dir, os.ModePerm)}return nil }测试 package zdpgo_fileimport "testing"func TestAddDir(t *testing.T) {data : […...
所学的全部课程的学生)
头歌OpenGauss数据库-I.复杂查询第5关:至少学了某位学生(Oliver)所学的全部课程的学生
本关任务:根据提供的表和数据,查询至少学了Oliver同学所学的全部课程的其他同学的信息(学号s_id,姓名`s_name)。 student表数据: s_ids_names_sex01Mia女02Riley男03Aria女04Lucas女05Oliver男06Caden男07Lily女08Jacob男course表数据: c_idc_namet_id01Chinese0202Math…...

【数据结构】哈夫曼树和哈夫曼编码
一、哈夫曼树 1.1 哈夫曼树的概念 给定一个序列,将序列中的所有元素作为叶子节点构建一棵二叉树,并使这棵树的带权路径长度最小,那么我们就得到了一棵哈夫曼树(又称最优二叉树) 接下来是名词解释: 权&a…...

深入探索微软Edge:领略新一代浏览器的无限可能
深入探索微软Edge:领略新一代浏览器的无限可能 在当今数字化时代,网络浏览器已经成为我们日常生活中不可或缺的一部分。而随着技术的不断进步,浏览器的功能和性能也在不断提升。微软Edge作为微软推出的全新一代浏览器,引领着浏览…...

JavaScript表达式和运算符
表达式 表达式一般由常量、变量、运算符、子表达式构成。最简单的表达式可以是一个简单的值。常量或变量。例:var a10 运算符 运算符一般用符号来表示,也有些使用关键字表示。运算符由3中类型 1.一元运算符:一个运算符能够结合一个操作数&…...
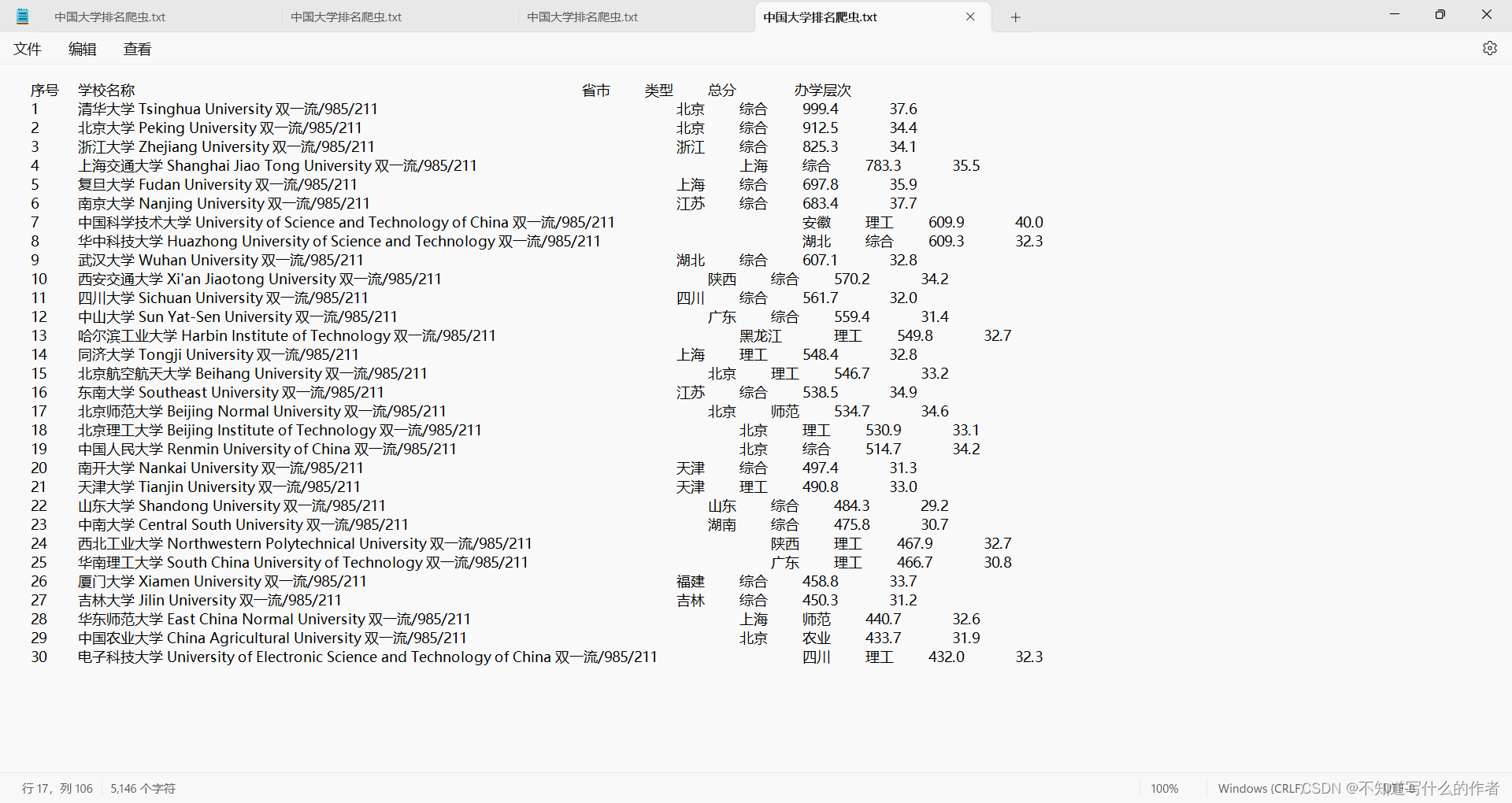
爬虫实训案例:中国大学排名
近一个月左右的时间学习爬虫,在用所积累的知识爬取了《中国大学排名》这个网站,爬取的内容虽然只是可见的文本,但对于初学者来说是一个很好的练习。在爬取的过程中,通过请求数据、解析内容、提取文本、存储数据等几个重要的内容入…...

C++ IO流
C标准IO流 使用cout进行标准输出,即数据从内存流向控制台(显示器)使用cin进行标准输入,即数据通过键盘输入到程序中使用cerr进行标准错误的输出使用clog进行日志的输出 C文件IO流 文件流对象 ofstream:只写 ofstream 是 C 中用于输出文件…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
