神经网络学习
神经网络学习
- 导语
- 数据驱动
- 驱动方法
- 训练/测试数据
- 损失函数
- 均方误差
- 交叉熵误差
- mini-batch
- 数值微分
- 梯度
- 梯度法
- 神经网络梯度
- 学习算法的实现
- 随机梯度下降
- 2层神经网络实现
- mini-batch实现
- 总结
- 参考文献
导语
神经网络中的学习指从训练数据中自动获取最优权重参数的过程,这个“最优”的定义在不同的应用场景下各有不同。
数据驱动
机器学习最关键的部分即如何对待数据,从数据当中找到模式,找到规律,找到答案。
驱动方法
机器学习的思路是,先从图像中提取特征量(一般由人设计),再用机器学习学习特征量的模式,神经网络的思路是,直接学习数据本身,特征量也是自主学习,区别图如下(来自书):
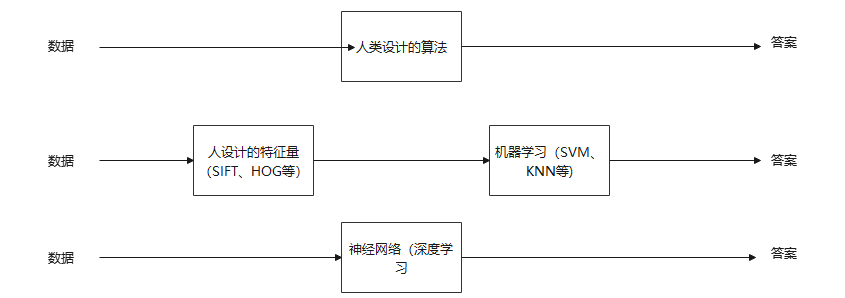 神经网络对所有的问题都用同样的流程解决,有时也被称为端到端机器学习(从输入直接获得输出)。
神经网络对所有的问题都用同样的流程解决,有时也被称为端到端机器学习(从输入直接获得输出)。
训练/测试数据
训练数据用来学习和找到最优的参数,测试数据用来评价模型的泛化能力,判断已训练的模型效果如何。
泛化能力即处理未被观察过的数据(简单说就是训练数据之外的数据)的能力,机器学习的目标就是获得这种能力。
为了提高泛化能力,对一个模型往往使用多个数据集进行考察,如果只使用一个数据集的话,可能会导致模型在这个数据集上表现很好,但是直接拿来检测新的数据时表达很差,这种只对某个数据集过度拟合的状态就是过拟合。
损失函数
为了评估每次训练的结果,神经网络采用了损失函数这一指标,这个损失函数有多种取法,书上给了几种函数及其实现方式。
均方误差
均方误差是常用的损失函数,表达式为(仅两个数据比对): E = 1 2 ∑ k ( y k − t k ) 2 E=\frac{1}{2}\mathop{\sum}\limits_k(y_k-t_k)^2 E=21k∑(yk−tk)2。
y k y_k yk为神经网络输出, t k t_k tk为监督数据, k k k为数据的维数,一般用one-hot表示(正解标签为1,其他为0)。
python实现:
def mean_squared_error(y,t):return 0.5*np/sum((y-t)**2)
交叉熵误差
交叉熵误差表达式为: E = − ∑ k t k l n y k E=-\mathop{\sum}\limits_kt_klny_k E=−k∑tklnyk,也用one-hot标签,python的实现很简单,如下:
def cross_entropy_error(y,t):return -np.sum(t*np.log(y))
这个实现方法看起来没什么问题,但是如果熟悉 l n x lnx lnx曲线的话就会知道,当 y y y存在0项时, l n 0 ln0 ln0的值是无穷大,是无法运算的,因此需要添加一个微小值防止负无穷大,更改之后的函数实现如下:
def cross_entropy_error(y,t):delta=1e-8return -np.sum(t*np.log(y+delta))
mini-batch
上述给出的实现和式子都是只针对只有一个值的情况,实际上,神经网络是一批一批地处理数据的,当要求处理大量数据时,书上以交叉熵误差为例,式子表达为: E = − 1 N ∑ n ∑ k t n k l n y n k E=-\frac{1}{N}\mathop{\sum}\limits_n\mathop{\sum}\limits_kt_{nk}lny_{nk} E=−N1n∑k∑tnklnynk。
其中, t n k t_{nk} tnk表示第 n n n个数据的第 k k k个元素值, y n k y_{nk} ynk是输出, t n k t_{nk} tnk是监督数据。
一般来说,由于数据集的数据量很大,用全部数据来计算损失函数是不适合的,因此mini-batch应运而生(从全部数据随机选出一部分,作为整体的近似),可以理解为现实中的抽样调查。
mini-batch的交叉熵实现:
def cross_entropy_error(y,t):if y.ndim==1:t=t.reshape(1,t.size)y=y.reshape(1,y.size)batch_size=y.shape[0]return -np.sum(t.np.log(y+1e-8))/batch_size#one-hot表示#return -np.sum(np.log(y[np.arange(batch_size),t]+1e-8))/batchsize#非one-hot表示
数值微分
书上在这里介绍了导数(用割线来代替)、求导、偏导等概念,如果有高等数学基础,应该很容易能理解这些,因此跳过,直接从梯度开始。
梯度
梯度是建立在偏导数的基础上的,假设有变量 x 0 , x 1 , . . . . . . x n x_0,x_1,......x_n x0,x1,......xn,然后有偏导数 ∂ f ∂ x 0 , ∂ f ∂ x 1 . . . . . . , ∂ f ∂ x n \frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1}......,\frac{\partial f}{\partial x_n} ∂x0∂f,∂x1∂f......,∂xn∂f,由全部变量的偏导数汇成的向量就是梯度,书上python的实现如下:
def numerical_gradient(f,x):h=1e-4grad=np.zeros_like(x)#先生成一个全0数组for idx in range(x.size):#遍历输入tmp_val=x[idx]x[idx]=tmp_val+hfxh1=f(x)#f(x+h)x[idx] = tmp_val - hfxh2 = f(x)#f(x-h)grad[idx]=(fxh1-fxh2)/(2*h)x[idx]=tmp_valreturn grad
梯度指示的方向是各点函数值减小最多的方向,具体证明属于高数知识,略。
梯度法
对于机器学习中的损失函数,我们总是想让其达到最小,但是,损失函数一般很复杂,不能直接得到最小的取值,此时,梯度法就是很好的解决方案。
但梯度法不一定每次都能取到最值,根据高等数学的指示,梯度所指的方向更类似于极值,而非最值(根据寻求最大值和最小值分成梯度下降和梯度上升)。
梯度法的思路很简单,计算当前位置的梯度,然后函数的取值沿着梯度前进一定距离,然后在新的地方求梯度(移动多少书在后面解释了,和学习率有关),循环往复。
梯度法的数学表达式很简单: x = x − η ∂ f ∂ x x=x-η\frac{\partial f}{\partial x} x=x−η∂x∂f, η \eta η是更新量,也就是学习率,决定了每次移动的步长。
像学习率这种参数被称为超参数,因为它并不是神经网络自动学习获得的,在实际的训练过程中,往往需要尝试多个值,学习率过小,则迭代次数过多,训练的时间被无意义浪费,学习率过大,可能步子迈大了扯着蛋,越过了极值或最值。
书上将梯度法式子用python实现:
def gradient_descent(f,init_x,lr=0.01,step_num=100):x=init_x#初始化网络参数for i in range(step_num):grad=numerical_gradient(f,x)#计算梯度x-=lr*grad#向梯度方向移动return x
神经网络梯度
在理解了梯度的概念和用法之后,在神经网络中运用梯度就变得很容易了,将结果矩阵中的每个值对权重秋偏导即可,以一个 2 × 2 2×2 2×2的矩阵为例,表达式如下:
W = ( w 11 w 12 w 21 w 22 ) W= \begin{pmatrix} w_{11}&w_{12}\\ w_{21}&w_{22} \end{pmatrix} W=(w11w21w12w22)
∂ L ∂ W = ( ∂ L ∂ w 11 ∂ L ∂ w 12 ∂ L ∂ w 21 ∂ L ∂ w 22 ) \frac{\partial L}{\partial W}= \begin{pmatrix} \frac{\partial L}{\partial w_{11}}&\frac{\partial L}{\partial w_{12}}\\ & &\\ \frac{\partial L}{\partial w_{21}}&\frac{\partial L}{\partial w_{22}}\\ \end{pmatrix} ∂W∂L= ∂w11∂L∂w21∂L∂w12∂L∂w22∂L
python的实现如下:
def numerical_gradient(f, x):h = 1e-4 # 0.0001grad = np.zeros_like(x)#初始化一个全0数组it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])#设置迭代器#操作对象为多维,操作为读写while not it.finished:idx = it.multi_indextmp_val = x[idx]x[idx] = float(tmp_val) + hfxh1 = f(x) # f(x+h)x[idx] = tmp_val - h fxh2 = f(x) # f(x-h)grad[idx] = (fxh1 - fxh2) / (2*h)x[idx] = tmp_val # 还原值it.iternext() return grad
学习算法的实现
神经网络的学习过程大致包括这几个部分:选出mini-batch,计算梯度,更新参数,循环往复,理解起来很简单,最关键的部分就是前面提到的梯度及其更新的部分。
随机梯度下降
随机梯度下降的概述很简单,在原数据中随机选择mini batch的数据,然后再计算梯度,再根据梯度下降的方向移动,进行下一次运算,循环往复,一般将该函数命名为SGD。
2层神经网络实现
书上实现了一个两层神经网络的类,一些函数在前面已经写过,在此不再赘述,附带注释的代码如下:
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
from common.functions import *
from common.gradient import numerical_gradientclass TwoLayerNet:def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):#输入层神经元数,隐藏层神经元数,输出层神经元数# 初始化权重self.params = {}self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)#随机初始化权重,使用高斯分布self.params['b1'] = np.zeros(hidden_size)#偏置初始化为0self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)#随机初始化权重self.params['b2'] = np.zeros(output_size)def predict(self, x):#推理过程W1, W2 = self.params['W1'], self.params['W2']b1, b2 = self.params['b1'], self.params['b2']a1 = np.dot(x, W1) + b1z1 = sigmoid(a1)a2 = np.dot(z1, W2) + b2y = softmax(a2)return y# x:输入数据, t:监督数据def loss(self, x, t):y = self.predict(x)return cross_entropy_error(y, t)def accuracy(self, x, t):#计算精准度y = self.predict(x)y = np.argmax(y, axis=1)#重新排列成一维数组t = np.argmax(t, axis=1)accuracy = np.sum(y == t) / float(x.shape[0])return accuracy# x:输入数据, t:监督数据def numerical_gradient(self, x, t):#进行梯度下降loss_W = lambda W: self.loss(x, t)#获得损失值grads = {}grads['W1'] = numerical_gradient(loss_W, self.params['W1'])grads['b1'] = numerical_gradient(loss_W, self.params['b1'])grads['W2'] = numerical_gradient(loss_W, self.params['W2'])grads['b2'] = numerical_gradient(loss_W, self.params['b2'])#向梯度减小的方向移动return grads
mini-batch实现
书上以MNIST数据集为基础,用两层神经网络进行了学习,修改和加上注释后,代码和运行结果如下:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)#加载数据network = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)#创造一个神经网络类,隐藏层数据可以设置其他合理值iters_num = 10000 # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100#抽100个训练
learning_rate = 0.1train_loss_list = []
train_acc_list = []
test_acc_list = []iter_per_epoch = max(train_size / batch_size, 1)for i in range(iters_num):batch_mask = np.random.choice(train_size, batch_size)#选100个随机数x_batch = x_train[batch_mask]#获得下标t_batch = t_train[batch_mask]#获得下标# 计算梯度grad = network.numerical_gradient(x_batch, t_batch)#很慢,不如反向传播# 更新参数for key in ('W1', 'b1', 'W2', 'b2'):network.params[key] -= learning_rate * grad[key]loss = network.loss(x_batch, t_batch)#计算损失train_loss_list.append(loss)if i % iter_per_epoch == 0:#每次算完一小批就输出一次结果train_acc = network.accuracy(x_train, t_train)test_acc = network.accuracy(x_test, t_test)train_acc_list.append(train_acc)test_acc_list.append(test_acc)print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
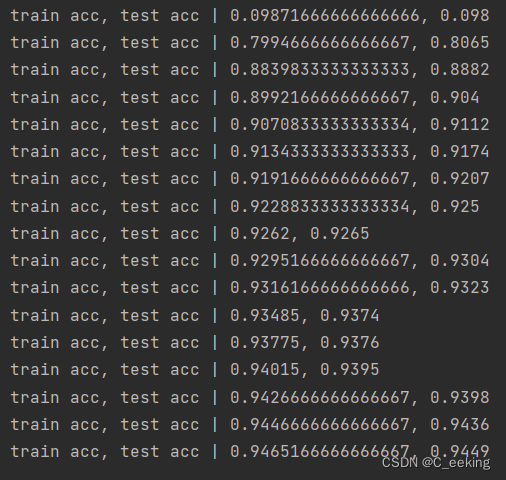
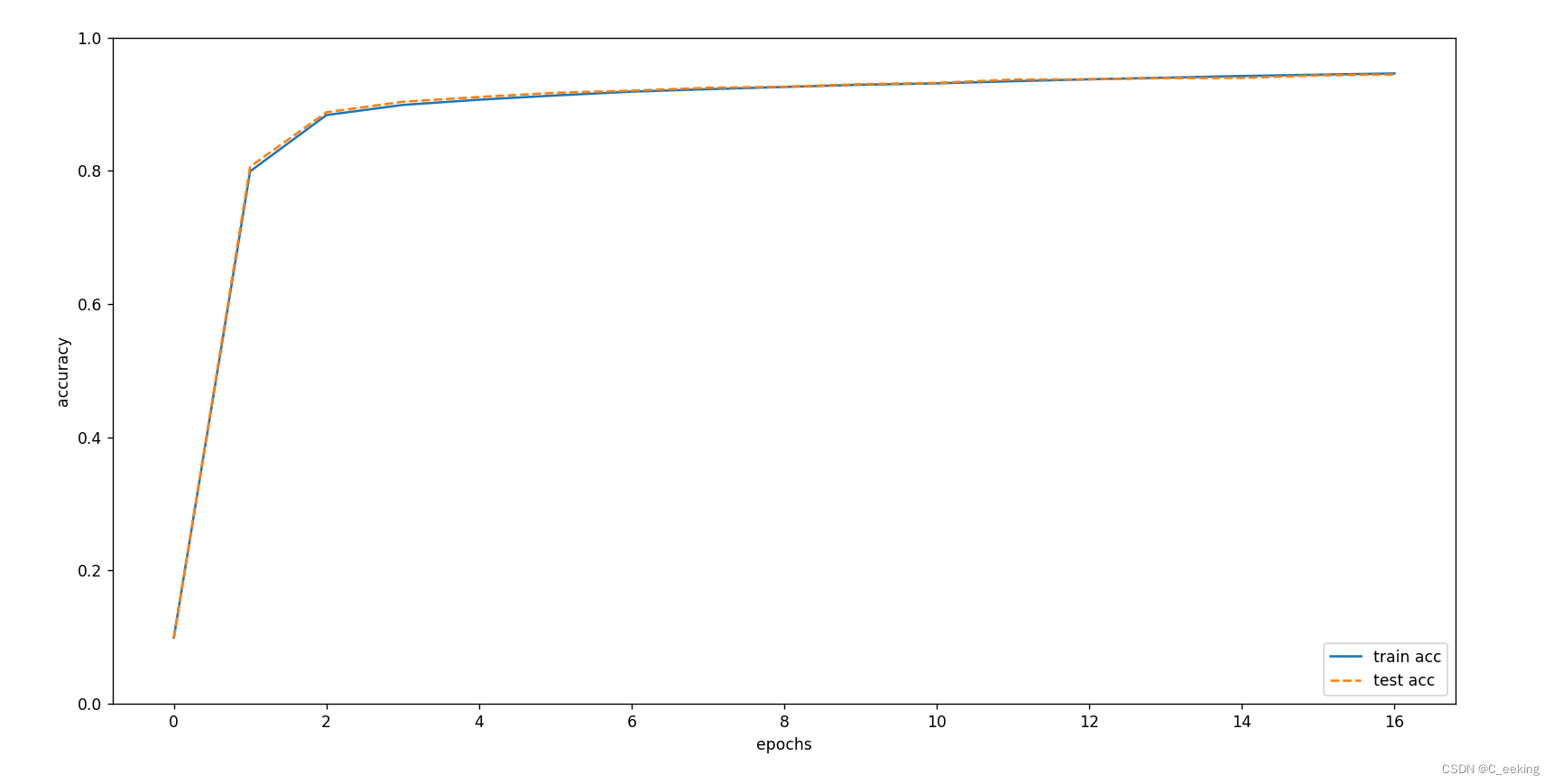
代码循环次数为10000,每一次都随机抽100个进行学习,计算损失函数值,输出一次学习结果,记录准确率,可以明显的看到准确率在逐渐增加,一般来说,准确率的增加也有可能意味着过拟合的出现,但是可以从图中看到,随着学习进行,训练数据和测试数据的精度几乎同步上升,且基本重合,因此可以说没有出现过拟合。
总结
神经网络的学习中有许多重要的概念,如梯度、损失函数、梯度下降等,在弄清楚了这些之后就能更好的理解神经网络的学习过程。
参考文献
- 《深度学习——基于Python的理论实现》
相关文章:

神经网络学习
神经网络学习 导语数据驱动驱动方法训练/测试数据 损失函数均方误差交叉熵误差mini-batch 数值微分梯度梯度法神经网络梯度 学习算法的实现随机梯度下降2层神经网络实现mini-batch实现 总结参考文献 导语 神经网络中的学习指从训练数据中自动获取最优权重参数的过程࿰…...

CentOS部署NFS
NFS服务端 部署NFS服务端 sudo yum install -y nfs-utils挂载目录 给 NFS 指定一个存储位置,也就是网络共享目录。一般来说,应该建立一个专门的 /data 目录,方便起见使用临时目录 /tmp/nfs: mkdir -p /tmp/nfs #修改权限 chmo…...

JWT使用方法
目录 基础概念 依赖 生成令牌 工具类 控制层 解析令牌 工具类 网关过滤器 效果 基础概念 Json web token (JWT), 是为了在网络应用环境间传递声明而执行的一种基于JSON的开放标准((RFC 7519).该token被设计为紧凑且安全的,特别适用于分布式站点…...

使用鱼香肉丝一键安装重新安装ROS后mavros节点报错,.so文件不匹配
解决方案: 1、写在mavros相关软件,共卸载7个包 sudo apt-get remove ros-melodic-mav*2、重新安装mavros,共安装10个包 sudo apt-get remove ros-melodic-mav*...
STM32+CubeMX移植SPI协议驱动W25Q16FLash存储器
STM32CubeMX移植SPI协议驱动W25Q16FLash存储器 SPI简介拓扑结构时钟相位(CPHA)和时钟极性( CPOL) W25Q16简介什么是Flash,有什么特点?W25Q16内部块、扇区、页的划分引脚定义通讯方式控制指令原理图 CubeMX配…...

gpt-4o考场安排
说明 :经过多次交互,前后花了几个小时,总算完成了基本功能。如果做到按不同层次分配考场,一键出打印结果就完美了。如果不想看中间“艰苦”的过程,请直接跳到“最后结果”及“食用方法”。中间过程还省略了一部分交互&…...
【Unity AR开发插件】四、制作热更数据-AR图片识别场景
专栏 本专栏将介绍如何使用这个支持热更的AR开发插件,快速地开发AR应用。 链接: Unity开发AR系列 插件简介 通过热更技术实现动态地加载AR场景,简化了AR开发流程,让用户可更多地关注Unity场景内容的制作。 “EnvInstaller…”支…...

Spring AOP的实操 + 原理(动态代理)
1 什么是Spring AOP 要想知道Spring AOP那必然是是要先知道什么是AOP了: AOP,全称为 Aspect-Oriented Programming(面向切面编程),是一种编程范式,用于提高代码的模块化,特别是横切关注点(cros…...
16.线性回归代码实现
线性回归的实操与理解 介绍 线性回归是一种广泛应用的统计方法,用于建模一个或多个自变量(特征)与因变量(目标)之间的线性关系。在机器学习和数据科学中,线性回归是许多入门者的第一个模型,它…...
Java进阶学习笔记1——课程介绍
课程适合学习的人员: 1)具备一定java基础的人员; 2)想深刻体会Java编程思想,成为大牛的人员; 学完有什么收获? 1)掌握完整的Java基础技术体系; 2)极强的编…...
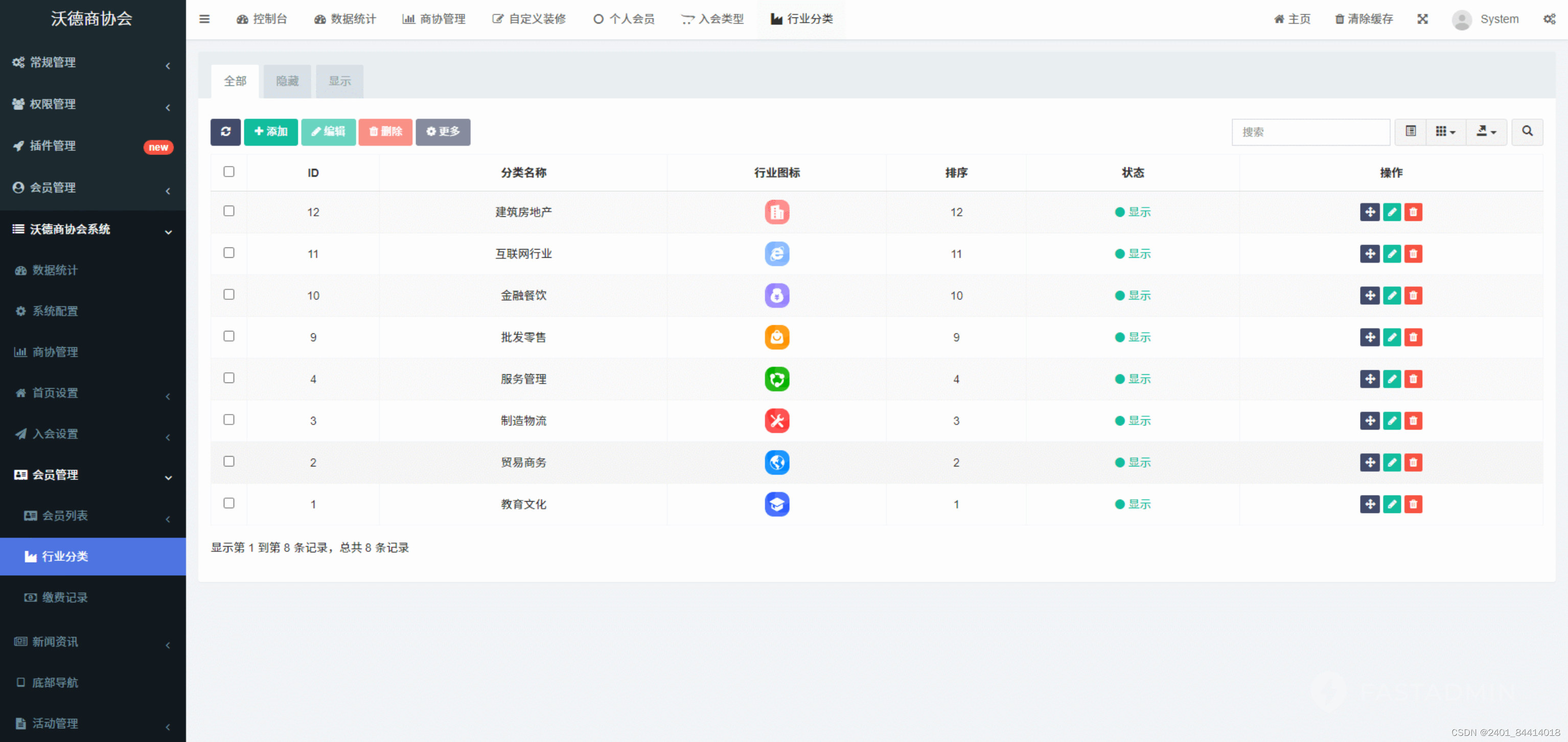
【全开源】沃德商协会管理系统源码(FastAdmin+ThinkPHP+Uniapp)
一款基于FastAdminThinkPHPUniapp开发的商协会系统,新一代数字化商协会运营管理系统,以“智慧化会员体系、智敏化内容运营、智能化活动构建”三大板块为基点,实施功能全场景覆盖,一站式解决商协会需求壁垒,有效快速建立…...
)
python毕设项目选题汇总(全)
各位计算机方面的毕业生们,是不是在头疼毕业论文写什么呢,我这给大家提供点思路: 网站系统类 《基于python的招聘数据爬虫设计与实现》 《基于python和Flask的图书管理系统》 《基于照片分享的旅游景点推荐系统》 《基于djangoxadmin的学生信…...

c#从数据库读取数据到datagridview
从已有的数据库读取数据显示到winform的datagridview控件,具体代码如下: //判断有无表 if (sqliteConn.State ConnectionState.Closed) sqliteConn.Open(); SQLiteCommand mDbCmd sqliteConn.CreateCommand(); m…...
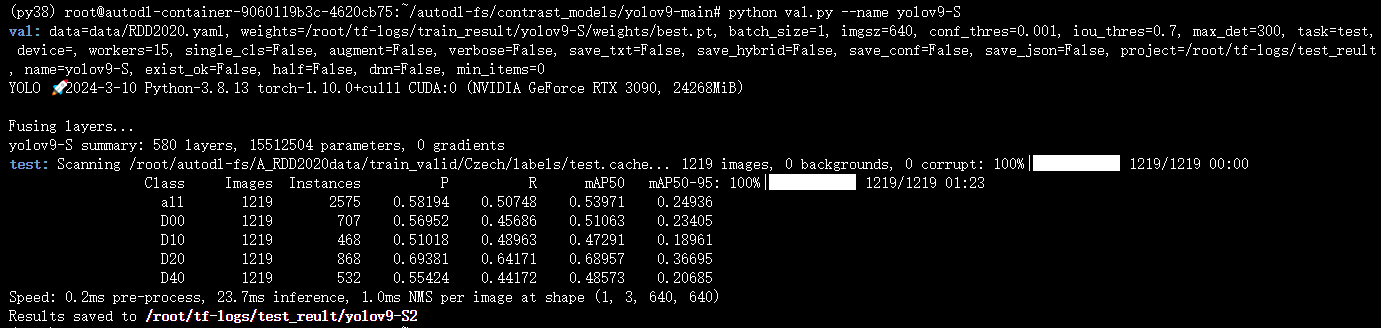
训练YOLOv9-S(注意:官方还没有提供YOLOv9-S的网络,我这是根据网络博客进行的步骤,按照0.33、0.50比例调整网络大小,参数量15.60M,计算量67.7GFLOPs)
文章目录 1、自己动手制造一个YOLOv9-S网络结构1.1 改前改后的网络结构(参数量、计算量)对比1.2 一些发现,YOLOv9代码打印的参数量计算量和Github上提供的并不一致,甚至yolov9-c.yaml代码打印出来是Github的两倍1.3 开始创造YOLOv…...

视觉检测实战项目——九点标定
本文介绍九点标定方法 已知 9 个点的图像坐标和对应的机械坐标,直接计算转换矩阵,核心原理即最小二乘拟合 {𝑥′=𝑎𝑥+𝑏𝑦+𝑐𝑦′=𝑎′𝑥+𝑏′𝑦+𝑐′ [𝑥1𝑦11𝑥2𝑦21⋮⋮⋮𝑥9𝑦91][𝑎𝑎′𝑏𝑏′𝑐𝑐′]=[𝑥1′𝑦…...

android git提交代码命令以及常见命令的使用
安装Git Ubuntu: sudo apt-get install git-core创建代码仓库: 配置身份: git config --global user.name "Tony" git confit --global user.email "tonygmail.com"查看身份: git config --global user.…...
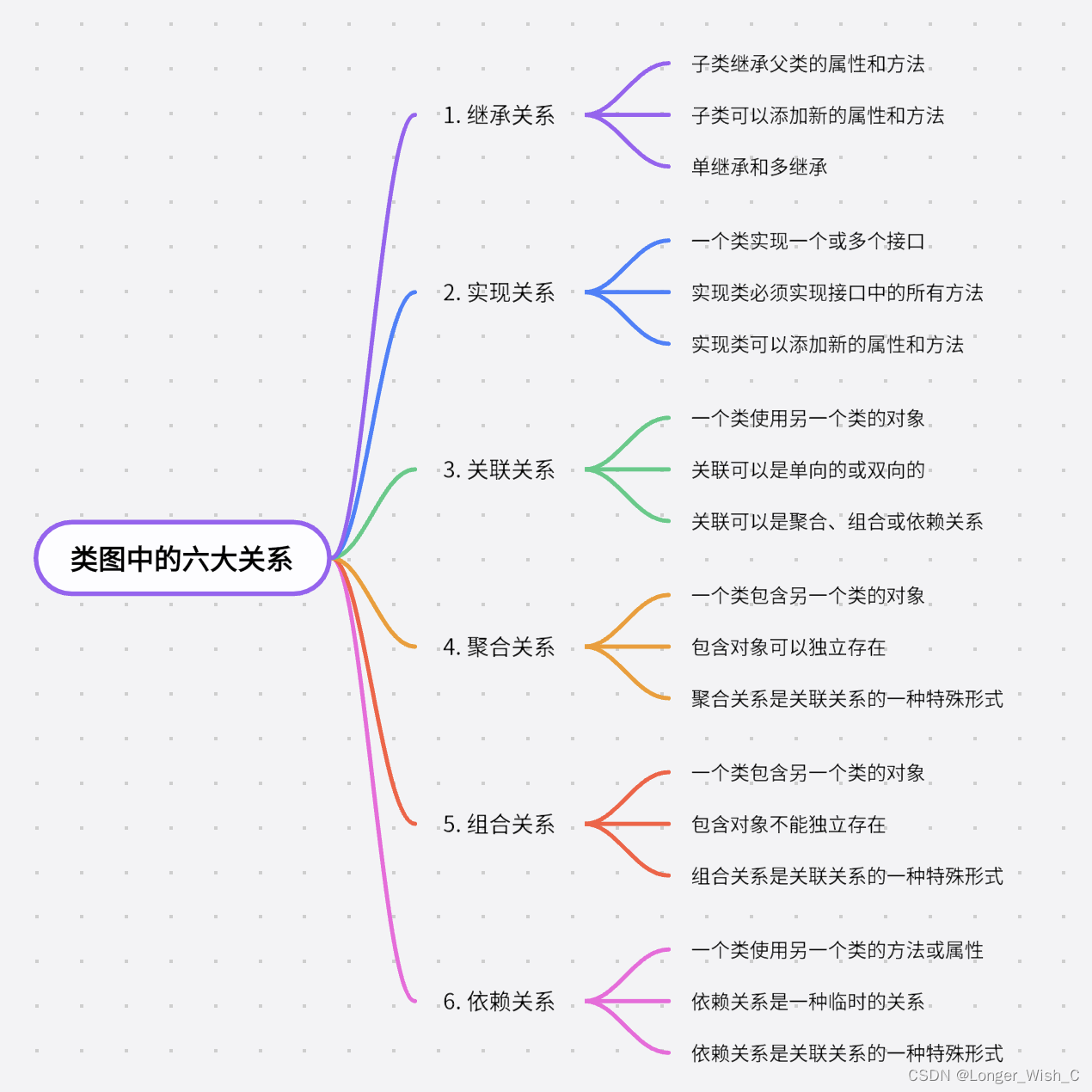
类图的六大关系
类图中的六大关系包括:继承关系、实现关系、关联关系、聚合关系、组合关系和依赖关系。 1. 继承关系 继承是一种类与类之间的关系,表示一种泛化和特化的关系。子类继承父类的特性和行为。 class Animal {void eat() {System.out.println("This an…...
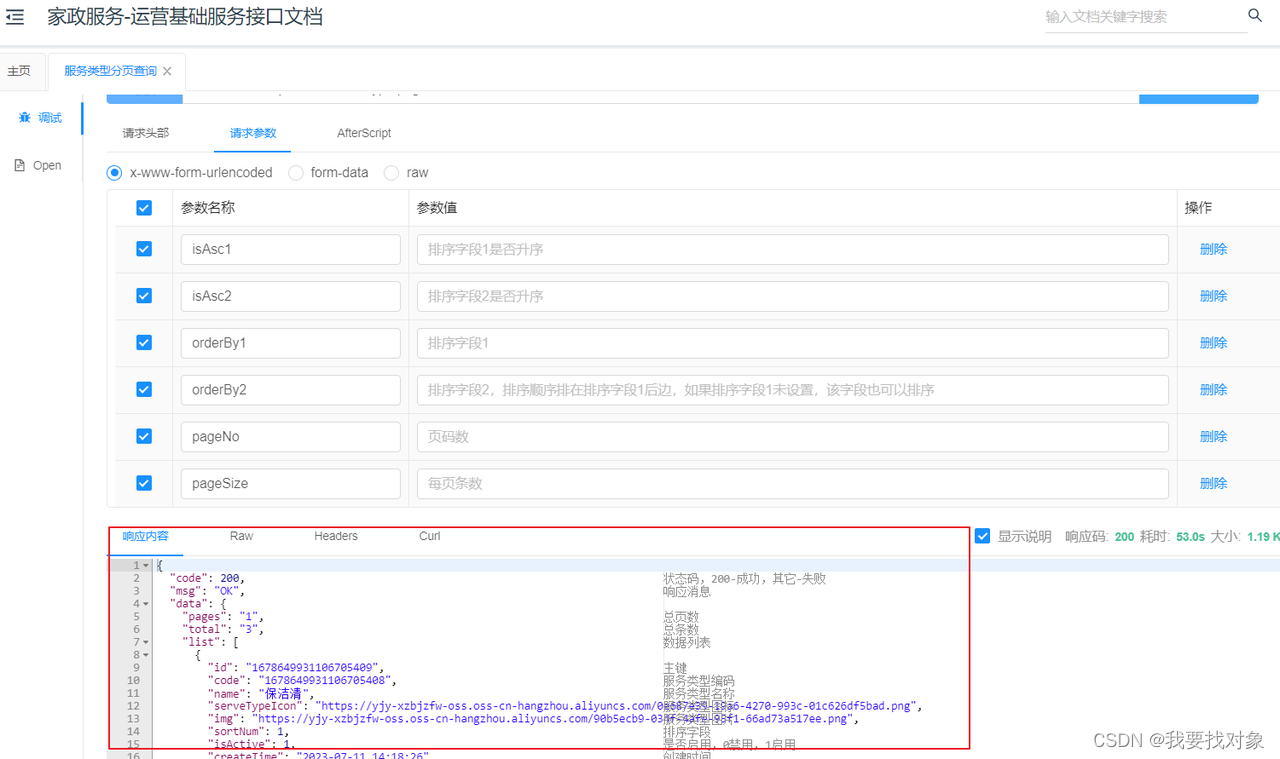
家政项目day2 需求分析(模拟入职后熟悉业务流程)
目录 1 项目主体介绍1.1 项目背景1.2 运营模式1.3 项目业务流程 2 运营端需求2.1 服务类型管理2.2 服务项目(服务)管理2.3 区域管理2.4 区域服务管理2.5 相关数据库表的管理2.6 设计工程结构2.7 测试接口(接口断点查看业务代码) 3…...

面试总结之:socket线路切换
"socket线路切换"通常指的是在网络通信过程中,根据当前网络状态或策略来动态更换数据传输路径的技术。这种技术可以提高通信的可靠性和性能。 在实际应用中,线路切换可能涉及到多种技术,例如: 负载均衡:根据每条路径的当前负载情况,动态地选择一条较为空闲的路…...

002 递归评论 mongodb websocket消息推送
文章目录 商品评论CommentController.javaComment.javaCommentServiceImpl.javaCommentRepository.javaCommentService.javaWebSocketConfig.javaWebSocketProcess.javaapplication.yamlproductReview.htmlindex.htmlindex.jsindex.css 订单评论EvaluateMapper.xmlEvaluateMapp…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
