SketchUp v2024 v24.0.553 解锁版安装教程 (强大的绘图三维建模工具)
前言
SketchUp(简称SU,俗称草图大师)全球知名的三维建模软件,强大的绘图工具、建模渲染、扩展插件和渲染器模板、海量3D模型库及建模灯光材质渲染效果图,用于建筑师、城市规划专家、游戏开发等行业。
一、下载地址
下载链接:http://dygod/ITSource 点击搜索: SketchUp
二、安装步骤
1、解压文件,解压后如下,点击执行【SketchUpStudioFull-2023-1-340-117.exe】
2、选择安装位置,点击【安装】
3、安装中,大概需要2-5分钟,耐心等待…
4、安装成功

5、返回解压到的文件,访问补丁文件夹,运行Patch.exe
6、在激活补丁中随便输入用户名,然后点击Patch按钮
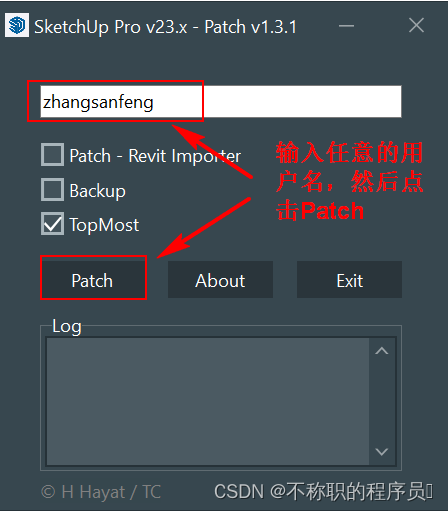
7、随后反复依次会弹3次弹框让你选择,不要疑惑
1)第一个 选择SketchUp安装根目录下的 SketchUp.exe 打开
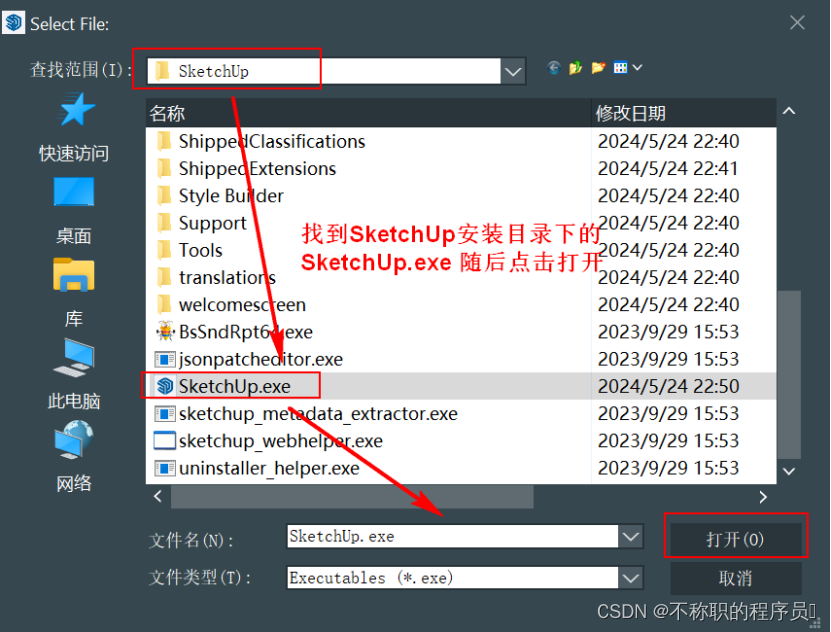
2)第二个访问SketchUp安装根目录LayOut文件夹,选择LayOut.exe打开
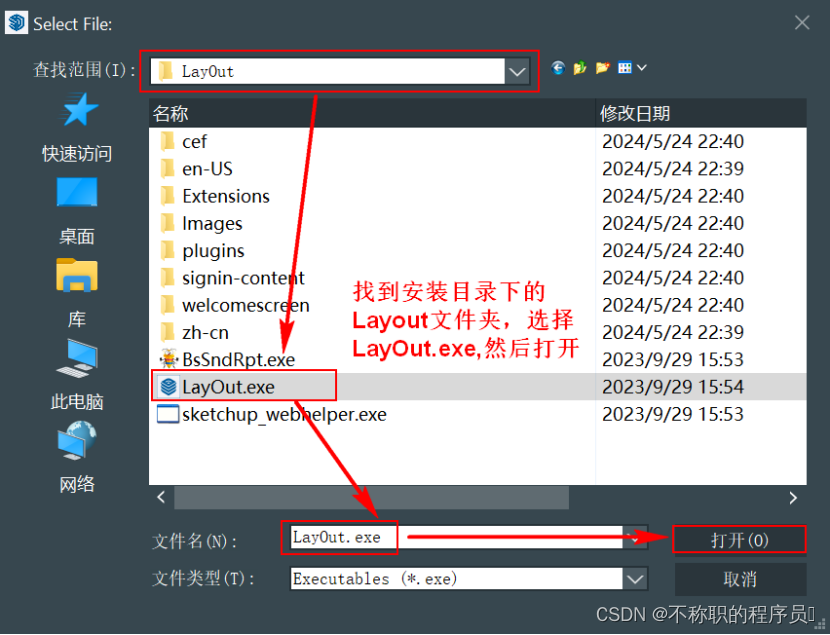
3)第三个访问SketchUp安装根目录Style Builder文件夹,选择Style Builder.exe打开
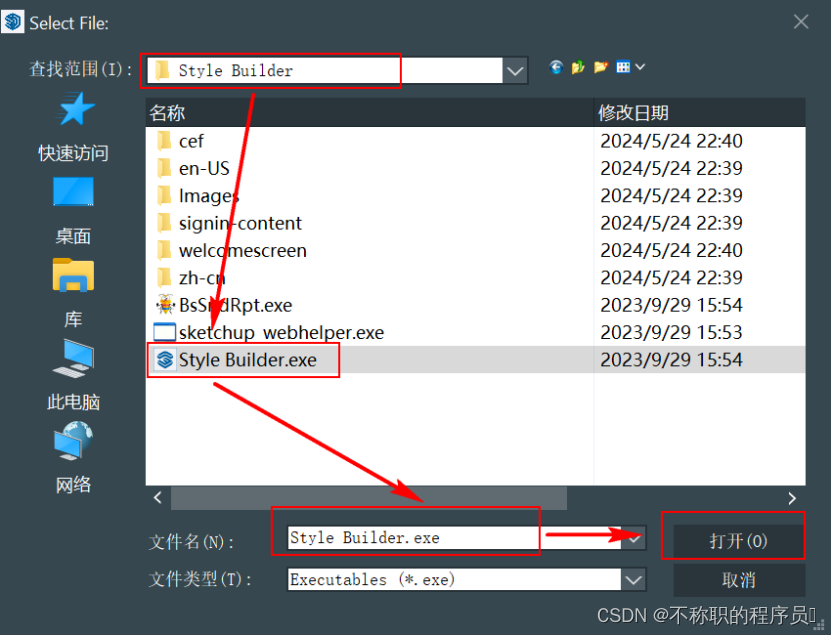
8、至此,激活成功
9、点击桌面图标启动

10、启动成功
相关文章:

SketchUp v2024 v24.0.553 解锁版安装教程 (强大的绘图三维建模工具)
前言 SketchUp(简称SU,俗称草图大师)全球知名的三维建模软件,强大的绘图工具、建模渲染、扩展插件和渲染器模板、海量3D模型库及建模灯光材质渲染效果图,用于建筑师、城市规划专家、游戏开发等行业。 一、下载地址 …...

力扣题解记录
三元组队列、取出元组中的元素:腐烂的橘子...
Flutter 中的 ExpandIcon 小部件:全面指南
Flutter 中的 ExpandIcon 小部件:全面指南 Flutter 提供了一系列的动画图标,ExpandIcon 就是其中之一,它用于表示一个可以展开或收起的内容区域。这个小部件通常用于实现折叠列表、手风琴菜单或其他类似的UI元素。本文将为您提供一个全面的指…...

想转行程序员的朋友,有什么想问的在评论区随便问,我知道的都告诉你。
你想转行程序员吗? 我自己是法学院毕业后,通过2年的努力才转行程序员成功的。 我发现对于一个外行来说,找不到一个适合自己的方向,光靠努力在一个新的行业里成功异常艰难。即使你非常努力,但方向错了也会做大量的无用…...
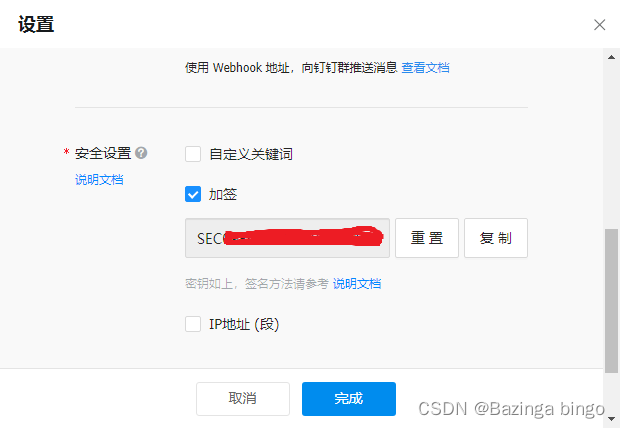
Jenkins工具系列 —— 通过钉钉API 发送消息
文章目录 钉钉环境搭建使用钉钉API接口 发送消息机器人安全设置使用自定义关键词机器人安全设置使用加签方式 资料下载 钉钉环境搭建 在jenkins安装钉钉插件以及小机器人,这部分内容可参考:插件 钉钉发送消息 使用钉钉API接口 发送消息 机器人安全设置…...
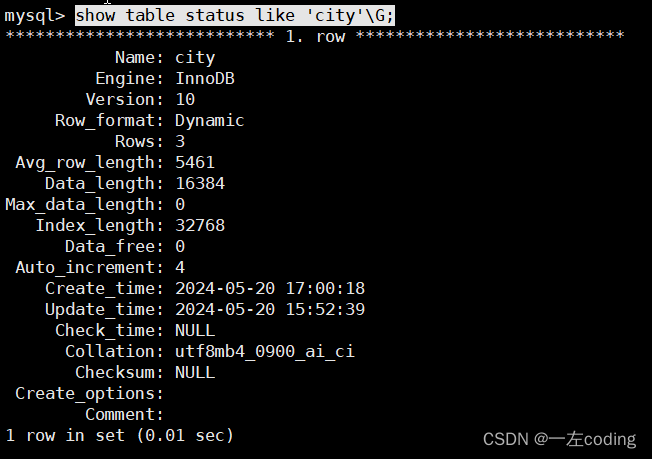
MySQL--存储引擎
一、存储引擎介绍 1.介绍 存储引擎相当于Linux的文件系统,以插件的模式存在,是作用在表的一种属性 2.MySQL中的存储引擎类型 InnoDB、MyISAM、CSV、Memory 3.InnoDB核心特性的介绍 聚簇索引、事务、MVCC多版本并发控制、行级锁、外键、AHI、主从复制特…...
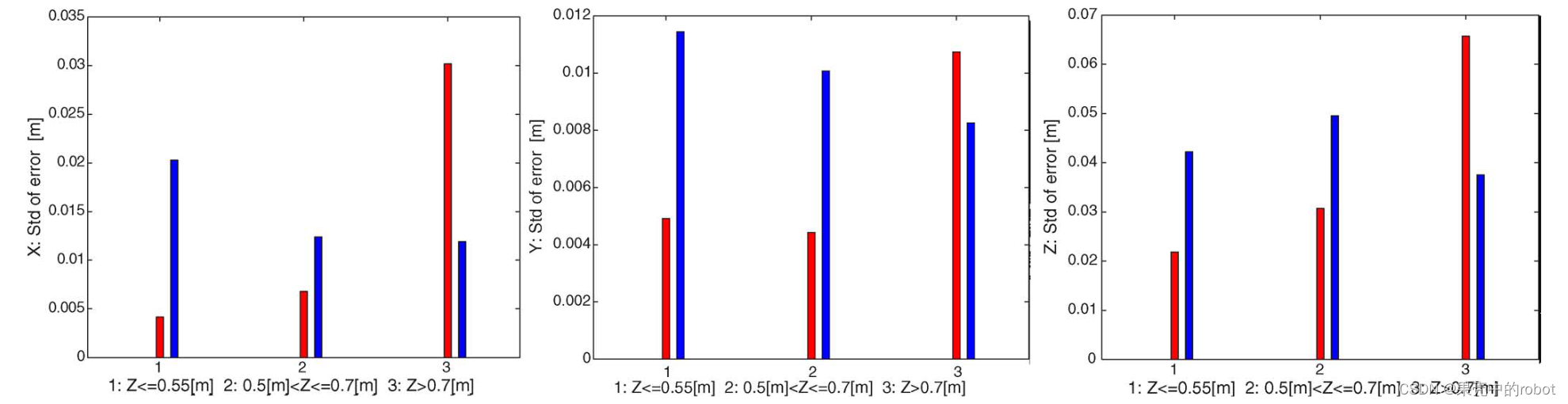
【经典文献】光-声立体成像:关于系统标定与三维目标重建
论文名称:《Opti-Acoustic Stereo Imaging: On System Calibration and 3-D Target Reconstruction》作者列表:Shahriar Negahdaripour, Hicham Sekkati, and Hamed Pirsiavash作者单位:美国迈阿密大学电气与计算机工程系,佛罗里达…...

弘君资本股市行情:股指预计保持震荡上扬格局 关注汽车、银行等板块
弘君资本指出,近期商场体现全体分化,指数层面上看,沪指一路震动上行,创出年内新高,创业板指和科创50指数体现相对较弱,依然是底部震动走势。从盘面体现上看,轮动依然是当时商场的主基调…...

看这两位东北圣女美吗?如何描写美女的大长腿?
看这两位东北圣女美吗?如何描写美女的大长腿? 最近署名为懂球娘娘的一篇描写东北圣女的文章火了,文中描述了海棠朵朵与辛芷蕾这两位娇媚动人的角色。其美艳动人的形象和魅力四溢的描写让人为之倾倒。 这种通过文字展现人物魅力的能力让人佩服…...
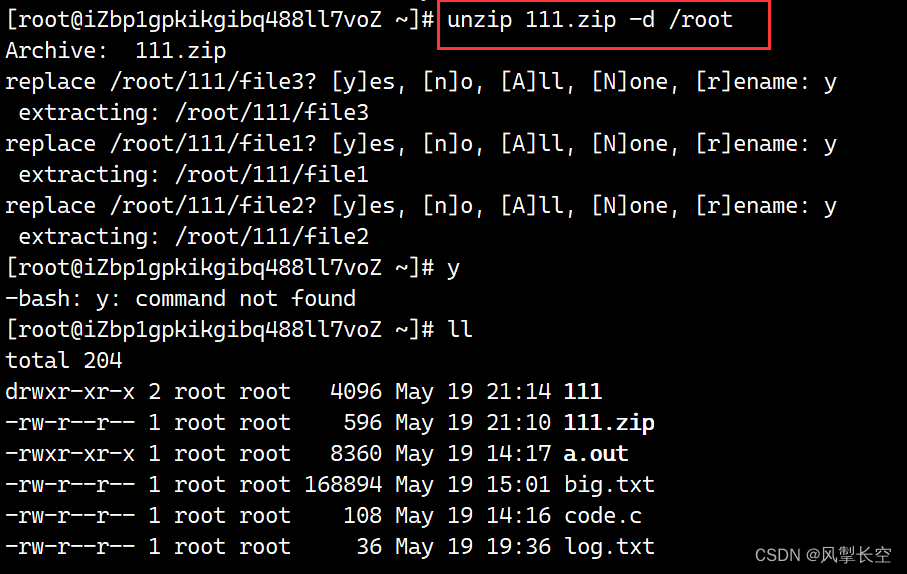
Linux相关指令
目录 1、输出重定向 2、追加重定向 3、输出重定向 4、more 5、less 6、head 7、tail 8、| (管道) 9、wc 10、与时间相关的指令 11、cal 12、find 13、grep 14、zip/unzip 1、输出重定向 在linux中,可以用echo向屏幕中输出字符串: 这是向屏幕…...

自建公式,VBA在Excel中解一元一次方程
自建公式,VBA在Excel中解一元一次方程 文章目录 前言一、运行效果图二、操作思路三、代码1.去除方程中未知数,将未知数转为“*0”2.计算方程中常数3.计算方程中未知数的系数一,先将未知数替换成“*1”4.计算方程中未知数的系数二5.计算方程得数前言 小学必考内容:一元一次…...

Linux-之 简易:Shell编程
1 为什么要学习Shell编程 对于JavaEE和Python程序员来说,工作的需要,你的老大会要求你编写一些Shel脚本进行程序或者是服务器的维护,比如编写一个定时备份数据库的脚本. 对于大数据程序员来说,需要编写Shell程序来管理集群 2 Shell是什么 Shell是一个命令行解释器ÿ…...

vue3的api风格
Vue的组件有两种不同的风格:组合式API 和 选项式API 选项式api 选项式API,可以用包含多个选项的对象来描述组件的逻辑,如:data,methods,mounted等。 组合式api setup:是一个标识,告…...
:开源 vs 养家糊口)
MySQL 开源到商业(五):开源 vs 养家糊口
前文提到,Oracle 收购了 Sun 之后,既没有像 Monty 预测的那样修改 MySQL 开源 License,也没有减少 MySQL 的研发投入。恰恰相反,Oracle 在持有 MySQL 知识产权的十几年里大幅提升了 MySQL 的工程质量,并且增加了很多用…...

进程信号(1)
目录 一、信号 1.1、生活中的信号 1.2、Linux中的信号 二、信号处理常见方式 三、信号的产生 3.1、简单理解信号的保存和发送 3.2、键盘产生信号 3.3、核心转储 3.4、系统调用接口产生信号 3.4.1、kill 3.4.2、raise 3.4.3、abort 3.5、软件条件产生信号 3.6、硬…...

Pytorch入门(7)—— 梯度累加(Gradient Accumulation)
1. 梯度累加 在训练大模型时,batch_size 最大值往往受限于显存容量上限,当模型非常大时,这个上限可能小到不可接受。梯度累加(Gradient Accumulation)是一个解决该问题的 trick梯度累加的思想很简单,就是时…...
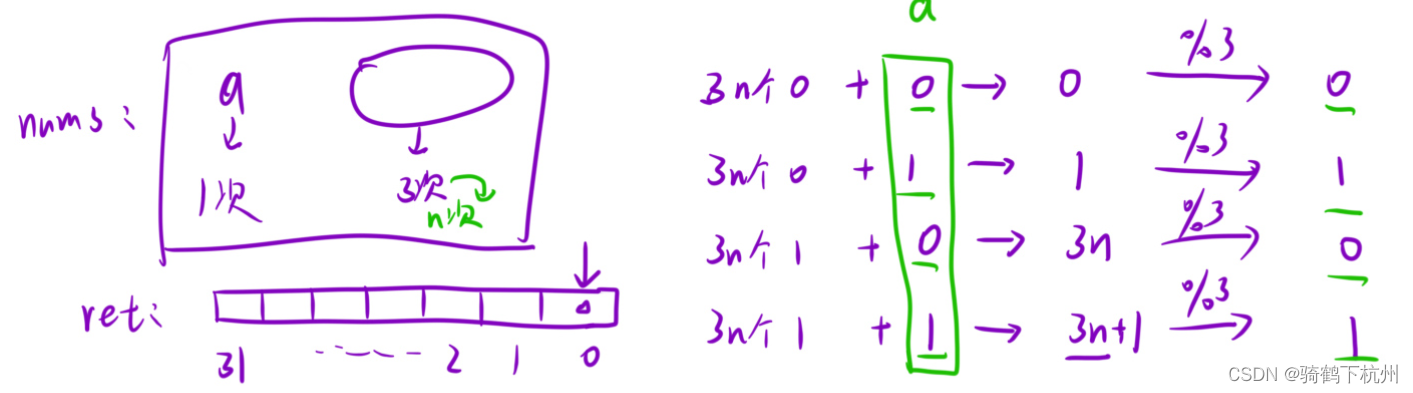
day12
第一题 本题我们可以使用以下方法: 方法一: 使用hash表<元素,出现次数>来统计字符串中不同元素分别出现的次数,当某一个元素的次数大于1时,返回false,如果每个元素的出现次数都为1,则返回…...

MySQL技术点合集
目录 1. MySQL目录 2. 验证是否首次登陆方法 3. 在Liunx中使用命令来输入sql语句方法 4. 获取修改密码 5. 关闭密码策略 6. 忘记MySQL密码找回 7. 旋转90度横向查看表 8. 添加一个远程连接的用户 1. MySQL目录 /usr/bin/mysql相关命令vim /etc/my.cnfmysql配置文件ls /…...

记录使用 Vue3 过程中的一些技术点
1、自定义组件,并使用 v-model 进行数据双向绑定。 简述: 自定义组件使用 v-model 进行传参时,遵循 Vue 3 的 v-model 机制。在 Vue 3 中,v-model 默认使用了 modelValue 作为 prop 名称,以及 update:modelValue 作为…...

6. C++通过fork的方式实现高性能网络服务器
我们上一节课写的tcp我们发现只有第一个与之连接的人才能收发信息。他又很多的不足 高性能网络服务器 通过fork实现高性能网络服务器 我们通过fork进行改装之后就可以成百上千的用户进行连接访问,对于每一个用户来说我们都fork一个子进程。让后让每一个子进程都是…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
