自建公式,VBA在Excel中解一元一次方程
自建公式,VBA在Excel中解一元一次方程
文章目录
- 前言
- 一、运行效果图
- 二、操作思路
- 三、代码
- 1.去除方程中未知数,将未知数转为“*0”
- 2.计算方程中常数
- 3.计算方程中未知数的系数一,先将未知数替换成“*1”
- 4.计算方程中未知数的系数二
- 5.计算方程得数
前言
小学必考内容:一元一次方程。
只要将方程输入到Excel工作表单元格内,VBA代码可以快速识别方程未知数,求得未知数系数和常数值,使用自建公式,一拖一拉,快速求解一元一次方程。
一、运行效果图

二、操作思路
1、查找方程中未知数,未知数可以是”A-Z”和”a-z”遍历方程字符串,凡为以上字母,均将替换;
2、计算常数,将上述查询到的字母替换成“0”,将方程“=”两边分成两个数组,左边数组数值计算得数后(-1)后与右数数组数值相加;
3、计算未知数系数,将上述查询到的字母替换成“1”,将方程“=”两边分成两个数组,右边数组数值计算得数后(-1)后与左数数组数值相加,再加上2中得出的常数值,即为未知数系数。
4、常数除以未知数系数,即为未知数值。
优点:未知数可以是26个字母大小写,适用于大多数方程式。
缺点:常数只能是数值,不能是字母。
如不符合实际需求,有兴趣的童鞋可以修改未知数和常数的判断条件。
三、代码
1.去除方程中未知数,将未知数转为“*0”
Function DelX(str As String) As StringDim c As StringDim i As IntegerDim tmp As St相关文章:

自建公式,VBA在Excel中解一元一次方程
自建公式,VBA在Excel中解一元一次方程 文章目录 前言一、运行效果图二、操作思路三、代码1.去除方程中未知数,将未知数转为“*0”2.计算方程中常数3.计算方程中未知数的系数一,先将未知数替换成“*1”4.计算方程中未知数的系数二5.计算方程得数前言 小学必考内容:一元一次…...

Linux-之 简易:Shell编程
1 为什么要学习Shell编程 对于JavaEE和Python程序员来说,工作的需要,你的老大会要求你编写一些Shel脚本进行程序或者是服务器的维护,比如编写一个定时备份数据库的脚本. 对于大数据程序员来说,需要编写Shell程序来管理集群 2 Shell是什么 Shell是一个命令行解释器ÿ…...

vue3的api风格
Vue的组件有两种不同的风格:组合式API 和 选项式API 选项式api 选项式API,可以用包含多个选项的对象来描述组件的逻辑,如:data,methods,mounted等。 组合式api setup:是一个标识,告…...
:开源 vs 养家糊口)
MySQL 开源到商业(五):开源 vs 养家糊口
前文提到,Oracle 收购了 Sun 之后,既没有像 Monty 预测的那样修改 MySQL 开源 License,也没有减少 MySQL 的研发投入。恰恰相反,Oracle 在持有 MySQL 知识产权的十几年里大幅提升了 MySQL 的工程质量,并且增加了很多用…...

进程信号(1)
目录 一、信号 1.1、生活中的信号 1.2、Linux中的信号 二、信号处理常见方式 三、信号的产生 3.1、简单理解信号的保存和发送 3.2、键盘产生信号 3.3、核心转储 3.4、系统调用接口产生信号 3.4.1、kill 3.4.2、raise 3.4.3、abort 3.5、软件条件产生信号 3.6、硬…...

Pytorch入门(7)—— 梯度累加(Gradient Accumulation)
1. 梯度累加 在训练大模型时,batch_size 最大值往往受限于显存容量上限,当模型非常大时,这个上限可能小到不可接受。梯度累加(Gradient Accumulation)是一个解决该问题的 trick梯度累加的思想很简单,就是时…...
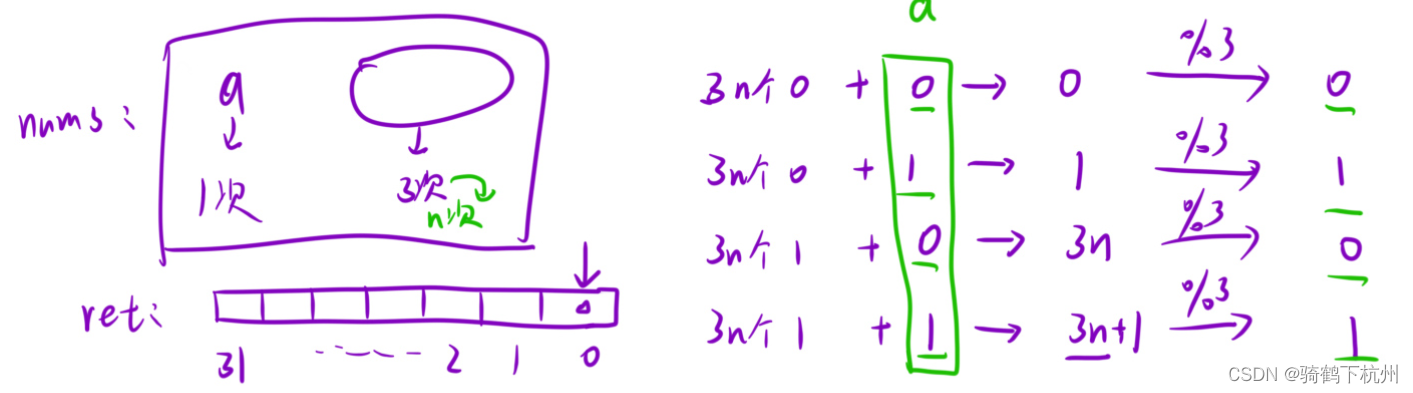
day12
第一题 本题我们可以使用以下方法: 方法一: 使用hash表<元素,出现次数>来统计字符串中不同元素分别出现的次数,当某一个元素的次数大于1时,返回false,如果每个元素的出现次数都为1,则返回…...

MySQL技术点合集
目录 1. MySQL目录 2. 验证是否首次登陆方法 3. 在Liunx中使用命令来输入sql语句方法 4. 获取修改密码 5. 关闭密码策略 6. 忘记MySQL密码找回 7. 旋转90度横向查看表 8. 添加一个远程连接的用户 1. MySQL目录 /usr/bin/mysql相关命令vim /etc/my.cnfmysql配置文件ls /…...

记录使用 Vue3 过程中的一些技术点
1、自定义组件,并使用 v-model 进行数据双向绑定。 简述: 自定义组件使用 v-model 进行传参时,遵循 Vue 3 的 v-model 机制。在 Vue 3 中,v-model 默认使用了 modelValue 作为 prop 名称,以及 update:modelValue 作为…...

6. C++通过fork的方式实现高性能网络服务器
我们上一节课写的tcp我们发现只有第一个与之连接的人才能收发信息。他又很多的不足 高性能网络服务器 通过fork实现高性能网络服务器 我们通过fork进行改装之后就可以成百上千的用户进行连接访问,对于每一个用户来说我们都fork一个子进程。让后让每一个子进程都是…...

直播美颜插件、美颜SDK详解:技术、功能与实现原理
今天,小编将详细解析直播美颜插件和美颜SDK的技术、功能以及实现原理。 一、美颜技术的背景与发展 1.1美颜技术的兴起 随着直播平台的普及,美颜SDK技术逐渐被集成到直播软件中,以满足用户对更美观、自然的直播效果的需求。 1.2美颜技术的…...

MyBatis入门(1)
目录 一、JDBC操作回顾 二、什么是MyBatis? 三、MyBatis入门 1、准备工作 (1)创建工程 (2)数据准备 2、配置数据库连接字符串 3、写持久层代码 4、单元测试 (1)使用IDEA自动成成测试类…...

打开服务器远程桌面连接不上,可能的原因及相应的解决策略
在解决远程桌面连接不上服务器的问题时,我们首先需要从专业的角度对可能的原因进行深入分析,并据此提出针对性的解决方案。以下是一些可能的原因及相应的解决策略: 一、网络连接问题 远程桌面连接需要稳定的网络支持,如果网络连接…...
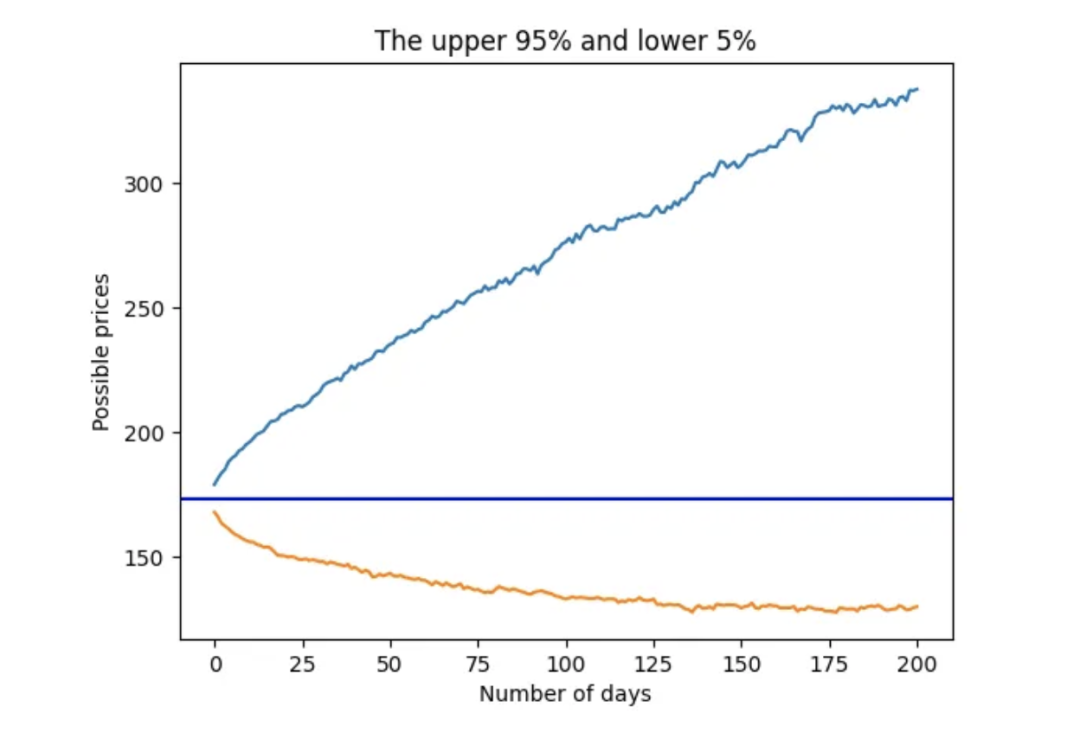
用于时间序列概率预测的蒙特卡洛模拟
大家好,蒙特卡洛模拟是一种广泛应用于各个领域的计算技术,它通过从概率分布中随机抽取大量样本,并对结果进行统计分析,从而模拟复杂系统的行为。这种技术具有很强的适用性,在金融建模、工程设计、物理模拟、运筹优化以…...

VScode解决报错“Remote-SSH XHR failed无法访问远程服务器“的方案
VScode解决报错"Remote-SSH XHR failed无法访问远程服务器"的方案 $ ls ~/.vscode-server/bin 2ccd690cbff1569e4a83d7c43d45101f817401dc稳定版下载链接:https://update.code.visualstudio.com/commit:COMMIT_ID/server-linux-x64/stable 内测版下载链接…...
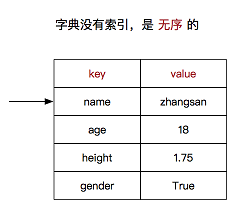
Python高级进阶--dict字典
dict字典⭐⭐ 1. 字典简介 dictionary(字典) 是 除列表以外 Python 之中 最灵活 的数据类型,类型为dict 字典同样可以用来存储多个数据字典使用键值对存储数据 2. 字典的定义 字典用{}定义键值对之间使用,分隔键和值之间使用:分隔 d {中…...
记忆力和人才测评,如何提升记忆力?
什么是记忆力? 如何通俗意义上的记忆力?我们可以把人的经历、经验理解成为一部纪录片,那么已经过去发生的事情,就是影片之前的情节,对于这些信息,在脑海里,人们会将其进行处理和组合ÿ…...

数据仓库建模
目录 数仓建模 为什么要对数据仓库进行分层 主题 主题的概念 维度建模: 模型的选择: 星形模式 雪花模型 星座模式 拉链表 维度表和事实表: 维度表 事实表 事实表设计规则 退化维度 事务事实表、周期快照事实表、累积快照事实…...

力扣:1738. 找出第 K 大的异或坐标值
1738. 找出第 K 大的异或坐标值 给你一个二维矩阵 matrix 和一个整数 k ,矩阵大小为 m x n 由非负整数组成。 矩阵中坐标 (a, b) 的 值 可由对所有满足 0 < i < a < m 且 0 < j < b < n 的元素 matrix[i][j](下标从 0 开始计数&…...

Keras深度学习框架第二十讲:使用KerasCV中的Stable Diffusion进行高性能图像生成
1、绪论 1.1 概念 为便于后文讨论,首先进行相关概念的陈述。 Stable Diffusion:Stable Diffusion 是一个在图像生成领域广泛使用的技术,尤其是用于文本到图像的转换。它基于扩散模型(Diffusion Models),这…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
