如何用 MoonBit 实现 diff?
你使用过 Unix 下的小工具 diff 吗?
没有也没关系,简而言之,它是一个比对两个文本文件之间有什么不同之处的工具。它的作用不止于此,Unix 下还有一个叫 patch 的小工具。
时至今日,很少有人手动为某个软件包打补丁了,但 diff 在另一个地方仍然保留着它的作用:版本管理系统。能够看见某一次提交之后的源码文件发生了哪些变化(并且用不同颜色标出来)是个很有用的功能。我们以当今最流行的版本管理系统 git 为例,它可以:
diff --git a/main/main.mbt b/main/main.mbt
index 99f4c4c..52b1388 100644
--- a/main/main.mbt
+++ b/main/main.mbt
@@ -3,7 +3,7 @@fn main {let a = lines("A\nB\nC\nA\nB\nB\nA")
- let b = lines("C\nB\nA\nB\nA\nC")
+ let b = lines("C\nB\nA\nB\nA\nA")let r = shortst_edit(a, b)println(r)}但是,究竟怎样计算出两个文本文件的差别呢?
git 的默认 diff 算法是 Eugene W. Myers在他的论文An O(ND) Difference Algorithm and Its Variations 中所提出的,这篇论文的 pdf 可以在网上找到,但论文内容主要集中于证明该算法的正确性。
在下文中,我们将以不那么严谨的方式了解该算法的基本框架,并且使用 MoonBit 编写该算法的一个简单实现。
01 定义"差别"及其度量标准
当我们谈论两段文本的"差别"时,我们说的其实是一系列的编辑动作,通过执行这段动作,我们可以把文本 a 转写成文本 b。
假设文本 a 的内容是:
A
B
C
A
B
B
A文本 b 的内容是:
C
B
A
B
A
C要把文本 a 转写成文本 b,最简单的编辑序列是删除每一个 a 中的字符(用减号表示),然后插入每一个 b 中的字符(用加号表示)。
- A
- B
- C
- A
- B
- B
- A
+ C
+ B
+ A
+ B
+ A
+ C但这样的结果对阅读代码的程序员可能没有什么帮助,而下面这个编辑序列就好很多,至少它比较短。
- A
- BC
+ BAB
- BA
+ C实际上,它是最短的可以将文本 a 转写成文本 b 的编辑序列之一,总共有5个动作。如果仅仅以编辑序列长度作为衡量标准,这个结果足以让我们满意。但当我们审视现实中已经存在的各种编程语言,我们会发现在此之外还有一些对用户体验同样重要的指标,让我们看看下面这两个例子:
// 质量好struct RHSet[T] {set : RHTable[T, Unit]}
+
+ fn RHSet::new[T](capacity : Int) -> RHSet[T] {
+ let set : RHTable[T, Unit]= RHTable::new(capacity)
+ { set : set }
+ }// 质量不好struct RHSet[T] {set : RHTable[T, Unit]
+ }
+
+ fn RHSet::new[T](capacity : Int) -> RHSet[T] {
+ let set : RHTable[T, Unit]= RHTable::new(capacity)
+ { set : set }}当我们在文件末尾处插入了一个新的函数定义,那计算出的编辑序列最好把更改都集中在后面。还有些类似的情况,当同时存在删除和插入时,最好不要计算出一个两种操作交织穿插的编辑序列,下面是另一个例子。
Good: - one Bad: - one- two + four- three - two+ four + five+ five + six+ six - threemyers 的 diff 算法能够满足我们在上面提到的这些需求,它是一种贪心算法,会尽可能地跳过相同的行(避免了在{前面插入文本的情况),同时它还会尽可能地把删除安排在插入前面,这又避免了后面一种情况。
02 算法概述
Myers 论文的基本想法是构建一张编辑序列构成的网格图,然后在这条图上搜索一条最短路径。我们沿用上面的例子 a = ABCABBA 和 b = CBABAC,建立一个 (x, y) 坐标网格。
0 1 2 3 4 5 6 70 o-----o-----o-----o-----o-----o-----o-----o| | | \ | | | | || | | \ | | | | | C| | | \ | | | | |
1 o-----o-----o-----o-----o-----o-----o-----o| | \ | | | \ | \ | || | \ | | | \ | \ | | B| | \ | | | \ | \ | |
2 o-----o-----o-----o-----o-----o-----o-----o| \ | | | \ | | | \ || \ | | | \ | | | \ | A| \ | | | \ | | | \ |
3 o-----o-----o-----o-----o-----o-----o-----o| | \ | | | \ | \ | || | \ | | | \ | \ | | B| | \ | | | \ | \ | |
4 o-----o-----o-----o-----o-----o-----o-----o| \ | | | \ | | | \ || \ | | | \ | | | \ | A| \ | | | \ | | | \ |
5 o-----o-----o-----o-----o-----o-----o-----o| | | \ | | | | || | | \ | | | | | C| | | \ | | | | |
6 o-----o-----o-----o-----o-----o-----o-----oA B C A B B A这张网格中左上方为起点(0, 0), 右下方为终点(7, 6)。沿着 x 轴向右前进一步为删除 a 中对应位置文本,沿 y 轴向下前进一步为插入 b 中对应位置文本,对角斜线标记的则是相同的文本,这些斜线可以直接跳过,它们不会触发任何编辑。
在编写实际执行搜索的代码之前,让我们先手动执行两轮搜索:
- 第一轮搜索起点为(0, 0),移动一步可以到达(0,1)和(1,0)。
- 第二轮搜索起点为(0,1)和(1,0),从(0,1)出发下移可以到达(0,2), 但是那里有一条通向(1,3)的斜线,所以最终落点为(1,3)。
整个myers算法的基础就是这样的广度优先搜索。
03 实现
虽然我们已经敲定了算法的基本思路,但仍有一些关键的设计需要考虑。算法的输入是两个字符串,但搜索需要在图上进行,如果真的把图构造出来再去搜索,这既非常浪费内存,也很费时间。
myers 算法的实现使用了一个聪明的想法,它定义了一个新的坐标 k = x - y。
- 右移一步会让k加一
- 左移一步会让k减一
- 沿对角线向左下方移动k值不变
让我们再定义一个坐标 d 用于代表搜索的深度,以 d 为横轴 k 为纵轴画出搜索过程的树状图:
| 0 1 2 3 4 5
----+--------------------------------------|4 | 7,3| /3 | 5,2| /2 | 3,1 7,5| / \ / \1 | 1,0 5,4 7,6| / \ \0 | 0,0 2,2 5,5| \ \
-1 | 0,1 4,5 5,6| \ / \
-2 | 2,4 4,6| \
-3 | 3,6可以看出来,在每一轮搜索中,k都严格地处于[-d, d]区间中(因为一次移动中最多也就能在上一轮的基础上加一或者减一), 且各点之间的k值间隔为2。myers算法的基本思路便源于此:通过遍历d和k进行搜索。当然了,它还需要保存每轮搜索的x坐标供下一轮搜索使用。
让我们首先定义Line结构体,它表示文本中的一行。
struct Line {number : Int // 行号text : String // 不包含换行
} derive(Debug, Show)fn Line::new(number : Int, text : String) -> Line {Line::{ number : number, text : text }
}然后定义一个辅助函数,它将一个字符串按照换行符分割成 Array[Line]。这里需要注意的是,行号是从1开始的。
fn lines(str : String) -> Array[Line] {let mut line_number = 0let buf = Buffer::make(50)let vec = []for i = 0; i < str.length(); i = i + 1 {let ch = str[i]buf.write_char(ch)if ch == '\n' {let text = buf.to_string()buf.reset()line_number = line_number + 1vec.push(Line::new(line_number, text))}} else {// 可能文本不以换行符为结尾let text = buf.to_string()if text != "" {line_number = line_number + 1vec.push(Line::new(line_number, text))}vec}
}接下来我们需要包装一下数组,使其支持负数索引,原因是我们要用k的值做索引。
type BPArray[T] Array[T] // BiPolar Arrayfn BPArray::make[T](capacity : Int, default : T) -> BPArray[T] {let arr = Array::make(capacity, default)BPArray(arr)
}fn op_get[T](self : BPArray[T], idx : Int) -> T {let BPArray(arr) = selfif idx < 0 {arr[arr.length() + idx]} else {arr[idx]}
}fn op_set[T](self : BPArray[T], idx : Int, elem : T) -> Unit {let BPArray(arr) = selfif idx < 0 {arr[arr.length() + idx] = elem} else {arr[idx] = elem}
}现在我们可以开始编写搜索函数了,不过,搜索出完整的路径是比较复杂的,我们的第一个目标是搜索出最短路径的长度(大小和搜索深度一样)。我们先展示它的基本框架:
fn shortst_edit(a : Array[Line], b : Array[Line]) -> Int {let n = a.length()let m = b.length()let max = n + mlet v = BPArray::make(2 * max + 1, 0)for d = 0; d < max + 1; d = d + 1 {for k = -d; k < d + 1; k = k + 2 {......}}
}通过最极端的情况(两段文本没有相同的行)可以推出最多需要搜索n + m步,最少需要搜索0步。故设变量max = n + m。数组v是以k为索引保存x值的历史记录,因为k的范围是[-d, d],这个数组的大小被设为2 * max + 1。
但即使到了这一步,接下来该怎么做还是挺不好想,所以我们暂且只考虑d = 0; k = 0的情况。此时一定在(0, 0)点。同时,假如两段文本的开头相同,那就允许直接跳过。我们将这一轮的最终坐标写入数组v。
if d == 0 { // d等于0 k也一定等于0x = 0y = x - kwhile x < n && y < m && a[x].text == b[y].text {// 跳过所有相同的行x = x + 1y = y + 1}v[k] = x
}在d > 0时,就需要用到上一轮存储的坐标信息了。当我们知道一个点的k值以及上一轮搜索中点的坐标时,v[k]的值其实很好推算。因为搜索每深入一步k的值只能加一或者减一,所以v[k]在搜索树中一定是从v[k - 1]或者v[k + 1]延伸出来的。接下来的问题是:以v[k - 1]为末端的和以v[k + 1]为末端的这两条路径,应该如何选择?
有两种边界情况:k == -d和k == d
- k == -d时,只能选择v[k + 1]
- k == d时,只能选择v[k - 1]
回顾一下我们之前提到的要求:尽可能地把删除安排在插入前面,这基本上意味着我们应该选择x值最大的前一个位置。
if k == -d {x = v[k + 1]
} else if k == d {x = v[k - 1] + 1 // 横向移动需要加一
} else if v[k - 1] < v[k + 1] {x = v[k + 1]
} else {x = v[k - 1] + 1
}合并一下这四个分支,我们得到这样的代码:
if k == -d || (k != d && v[k - 1] < v[k + 1]) {x = v[k + 1]
} else {x = v[k - 1] + 1
}综合上面的所有步骤,我们可以得到这样的代码:
fn shortst_edit(a : Array[Line], b : Array[Line]) -> Int {let n = a.length()let m = b.length()let max = n + mlet v = BPArray::make(2 * max + 1, 0)// v[1] = 0for d = 0; d < max + 1; d = d + 1 {for k = -d; k < d + 1; k = k + 2 {let mut x = 0let mut y = 0// if d == 0 {// x = 0// }if k == -d || (k != d && v[k - 1] < v[k + 1]) {x = v[k + 1]} else {x = v[k - 1] + 1}y = x - kwhile x < n && y < m && a[x].text == b[y].text {x = x + 1y = y + 1}v[k] = xif x >= n && y >= m {return d}}} else {abort("impossible")}
}由于数组的初始值为0,我们可以省略 d == 0 这个分支。
04 尾声
我们实现了一个不完整的myers算法,它完成了正向的路径搜索,在下一篇文章中,我们将实现回溯,还原出完整的编辑路径,并写一个可以输出彩色diff的打印函数。
本篇文章参考了:The Myers diff algorithm: part 2
感谢这篇博客的作者James Coglan。
相关文章:

如何用 MoonBit 实现 diff?
你使用过 Unix 下的小工具 diff 吗? 没有也没关系,简而言之,它是一个比对两个文本文件之间有什么不同之处的工具。它的作用不止于此,Unix 下还有一个叫 patch 的小工具。 时至今日,很少有人手动为某个软件包打补丁了…...

opencl色域变换,处理传递显存数据
在使用ffmpeg解码后的多路解码数据非常慢,还要给AI做行的加速方式是在显存处理数据,在视频拼接融合产品的产品与架构设计中,提出了比较可靠的方式是使用cuda,那么没有cuda的显卡如何处理呢 ,比较好的方式是使用opencl来…...
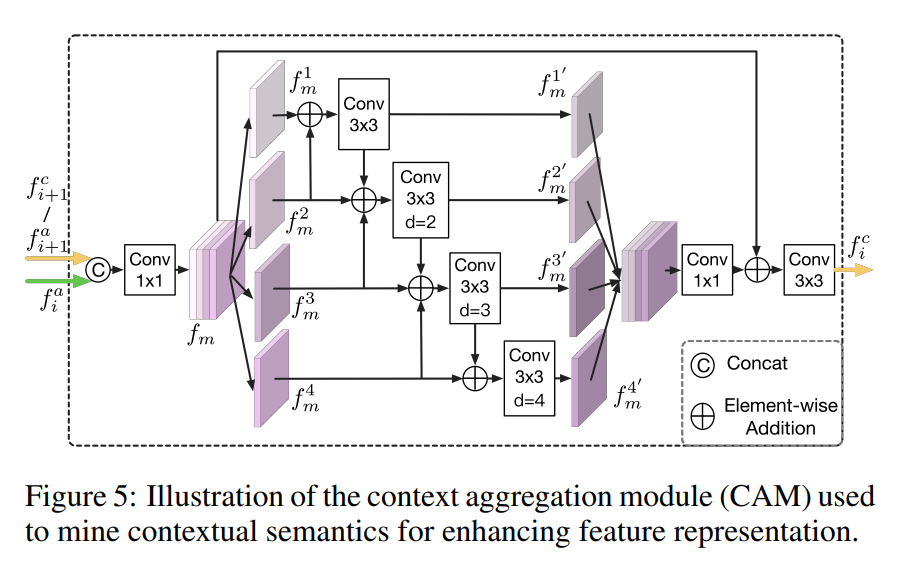
COD论文笔记 Boundary-Guided Camouflaged Object Detection
动机 挑战性任务:伪装物体检测(COD)是一个重要且具有挑战性的任务,因为伪装物体往往与背景高度相似,使得准确识别和分割非常困难。现有方法的不足:现有的深度学习方法难以有效识别伪装物体的结构和细节&am…...

java内存模型介绍
Java内存模型(Java Memory Model,JMM)是一种规范,它定义了Java虚拟机(JVM)如何在内存中存储和访问Java对象的方式,以及多个线程如何访问这些对象时的规则。它的主要目标是定义程序中的各个线程如…...
CSS语法介绍
文章目录 前言一、CSS引入方式1.行内操作2.内部操作3.外部操作 二、常用选择器1.标签选择器2.类选择器3.id选择器4.群组选择器5.后代选择器 三、字体常用设置1.字体类型2.字体大小3.字体样式4.字体粗细 四、div盒子模型1.盒子边框2.外边距3.内边距4.浮动 综合实战案例 前言 以…...
Jeecg | 完成配置后,如何启动整个项目?
前端启动步骤: 1. 以管理员身份打开控制台,切换到前端项目目录。 2. 输入 pnpm install 3. 输入 pnpm dev 4. 等待前端成功运行。 可以看到此时前端已经成功启动。 后端启动步骤: 1. 启动 mysql 服务器。 管理员身份打开控制台&#…...

Kubectl 的使用——k8s陈述式资源管理
一、kebuctl简介: kubectl 是官方的CLI命令行工具,用于与 apiserver 进行通信,将用户在命令行输入的命令,组织并转化为 apiserver 能识别的信息,进而实现管理 k8s 各种资源的一种有效途径。 对资源的增、删、查操作比较方便&…...

多天线技术
多天线技术可以分为两类:分集技术和空间复用技术。分集技术利用多天线接收或者发射载有同一信息的信号,提高传输的可靠性。分集技术是将瑞利衰落无线信道换成更加稳定的信道。 发射端未知CSI时的信道容量 发射端已知CSI时的信道容量 信道估计ÿ…...

Meta发布Chameleon模型预览,挑战多模态AI前沿
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
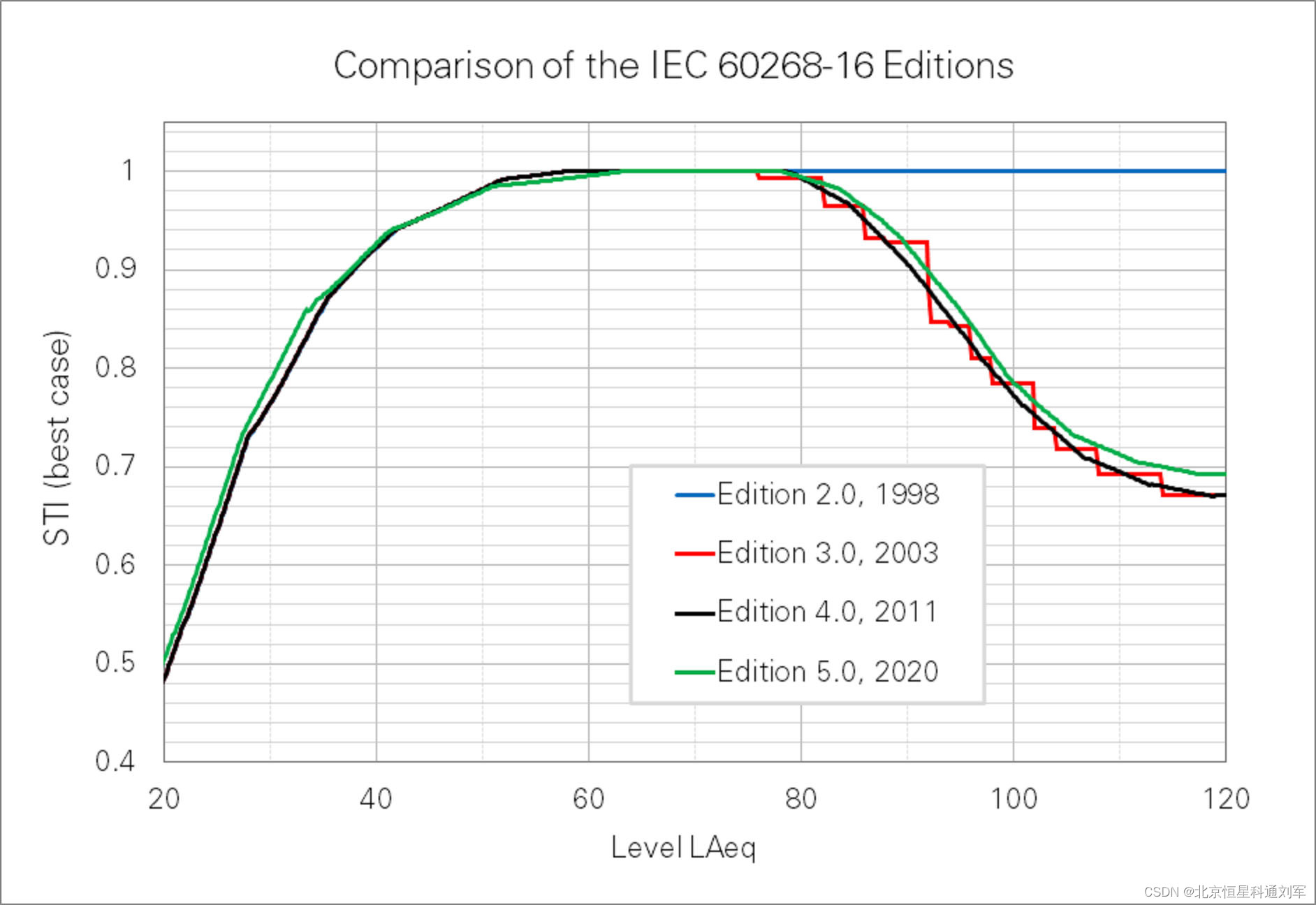
声压级越大,STIPA 越好,公共广播就越清晰吗?
在公共广播中,有些朋友经常问到是不是声压越大,广播清晰度就越高,下面我从搜集了一些专业技术资料,供大家参考。 一、声压级越大,STIPA 越好吗? 不完全是。最初,人们认为当声压级达到 60 dBA 以…...
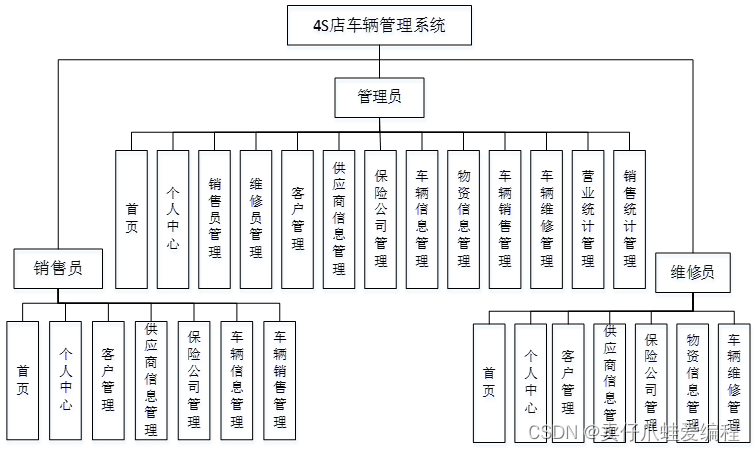
基于springboot+vue的4S店车辆管理系统
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
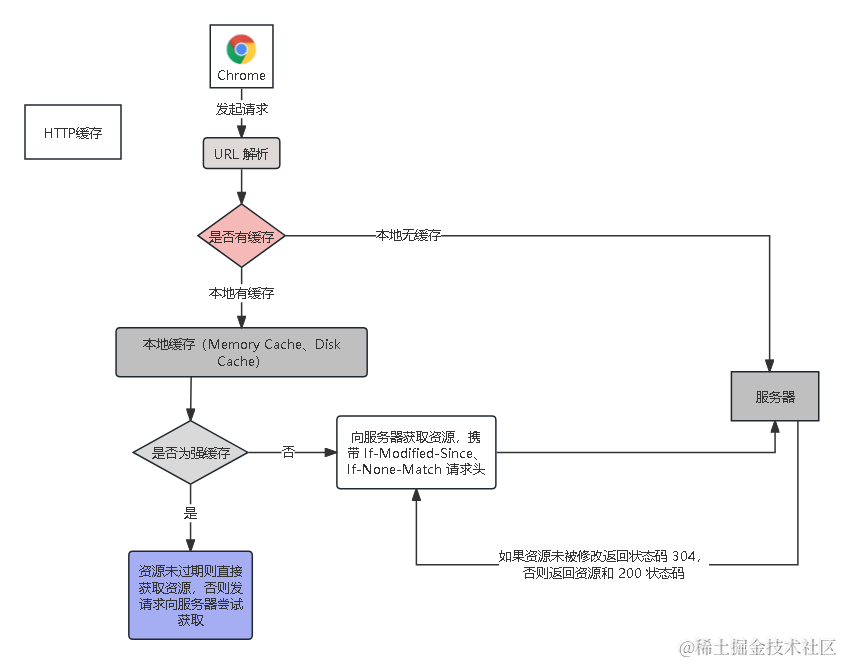
深入理解 HTTP 缓存
浏览器缓存不是本地存储,要分清。浏览器缓存分为强缓存和协商缓存。本篇文章参考:使用 HTTP 缓存防止不必要的网络请求 讲解之前,我画了个简图来解释浏览器从缓存中获取资源的过程。 1. 强缓存 强缓存是浏览器缓存机制中的一种,…...

upload-labs 通关方法
目录 Less-1(JS前端验证) Less-2(MIME验证) Less-3(黑名单,特殊过滤) Less-4(黑名单验证,.htaccess) Less-5(黑名单,点空格点绕过…...

5-26 Cpp学习笔记
1、如果子类实现了基类的函数,返回值、参数都相同,就覆盖了基类的函数。 2、使用作用域解析运算符来调用基类的函数。myDinner.Swim(); —— 调用子类的。myDinner.Fish::Swim(); —— 调用基类的(基类是Fish) 3、在子类中使用关键字using解除对Fish::…...

YOLOv8_pose的训练、验证、预测及导出[关键点检测实践篇]
1.关键点数据集划分和配置 从上面得到的数据还不能够直接训练,需要按照一定的比例划分训练集和验证集,并按照下面的结构来存放数据,划分代码如下所示,该部分内容和YOLOv8的训练、验证、预测及导出[目标检测实践篇]_yolov8训练测试验证-CSDN博客是重复的,代码如下: …...

架构师必考题--软件系统质量属性
软件系统质量属性 1.质量属性2.质量属性场景描述3.系统架构评估 这个知识点是系统架构师必考的题目,也是案例分析题第一题, 有时候会出现在选择题里面,考的分数也是非常高的。 1.质量属性 属性说明可用性错误检测/恢复/避免性能资源需求/管理…...
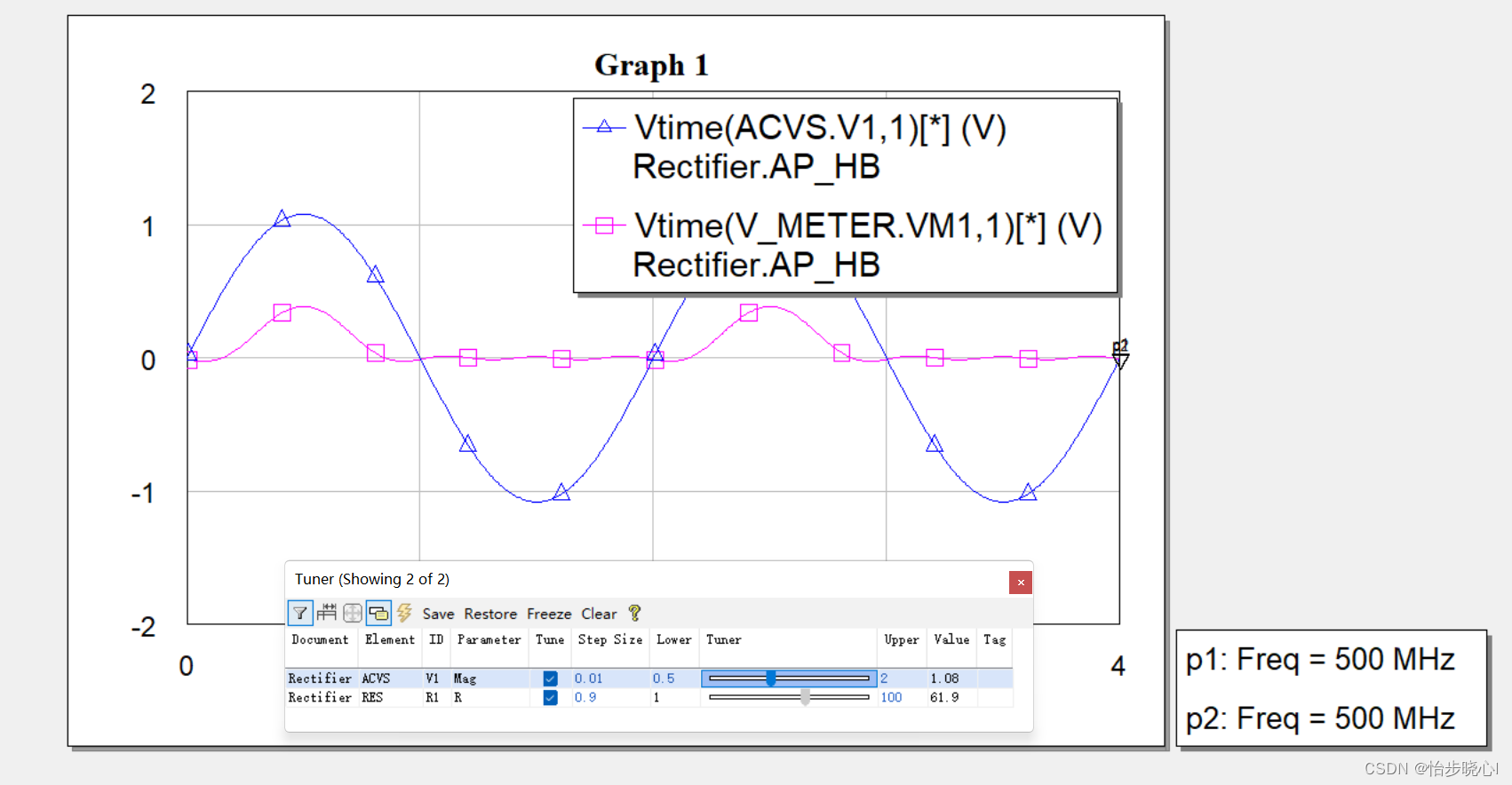
使用AWR对电路进行交流仿真---以整流器仿真为例
使用AWR对电路进行交流仿真—以整流器仿真为例 生活不易,喵喵叹气。马上就要上班了,公司的ADS的版权紧缺,主要用的软件都是NI 的AWR,只能趁着现在没事做先学习一下子了,希望不要裁我。 本AWR专栏只是学习的小小记录而…...

在UbuntuLinux系统上安装MySQL和使用
前言 最近开始计划在Ubuntu上写一个webserver的项目,看到一些比较好的类似的项目使用了MySQL,我就打算先把环境搞好跑一下试试,方便后面更进一步的学习。其实在本机windows上我已经有一个mysql,不过 在Unbuntu上安装MySQL 首先…...

React 如何自定义 Hooks
自定义 Hooks React 内部自带了很多 Hooks 例如 useState、useEffect 等等,那么我们为什么还要自定义 Hooks?使用 Hooks 的好处之一就是重用,可以将代码从组件中抽离出来定义为 Hooks,而不用每个组件中重复去写相同的代码。首先是…...

智能家居完结 -- 整体设计
系统框图 前情提要: 智能家居1 -- 实现语音模块-CSDN博客 智能家居2 -- 实现网络控制模块-CSDN博客 智能家居3 - 实现烟雾报警模块-CSDN博客 智能家居4 -- 添加接收消息的初步处理-CSDN博客 智能家居5 - 实现处理线程-CSDN博客 智能家居6 -- 配置 ini文件优化设备添加-CS…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...
