C++的红黑树
目录
基本概念
插入结点的颜色
判断性质是否破坏
调整方式
u为g的右孩子
u存在且为红
u存在且为黑
u不存在
结论
红黑树结点定义
代码实现
基本概念
1、红黑树是一种特殊的二叉搜索树,每个结点会增加一个存储位表示结点的颜色(红或黑)
2、红黑树通过对所有从根到叶子的路径上的各个结点的着色方式的限制,确保红黑树中没有一条路径会比其它路径长出两倍,从而使二叉搜索树接近平衡
3、AVL树是一个严格平衡(平衡因子,二叉树能做到的最好的平衡),而红黑树是一个近似平衡,插入100万个数据,AVL树会进行大量的旋转,形成的树可能是30层,但是红黑树的旋转会少一些,形成的树可能是60层,但是对于CPU而言其实二者差别也不大
4、红黑树有五个性质(紫色是重点):
- 每个结点不是红色就是黑色
- 根结点是黑色的
- 如果一个结点是红色,则它的两个孩子结点都是黑色(一个黑结点的孩子可以是红也可以是黑的,不可以不存在连续的红红、可以存在连续黑红、红黑和黑黑的结点)
- 对于每个结点,该结点到其所有后代叶子结点的简单路径上,均包含相同数目的黑色结点(一个结点向下的每条路径中的黑色结点相同,空结点也是黑色结点)(最难维护的规则)
- 每个叶子结点都是黑色的(红黑树中所指的叶子结点是空结点)

5、满足以上五条性质就能保证红黑树的最长路径 <= 最短路径 * 2
- 最短路径(极端情况):全黑(由性质4可得:其它路径中也有相同数目的黑色结点以及红色结点,但是全黑的路径中没有红色结点)
- 最长路径(极端情况):一黑一红(不算空结点)
- 一个红黑树肯定有最长或最短路径,只不过不一定有以上的理想情况下的最短和最长路径,正常情况下最长路径小于最短路径的2倍,极端情况下最长路径可能还会等于最短路径的2倍(没有极端情况就矮子里挑将军了)
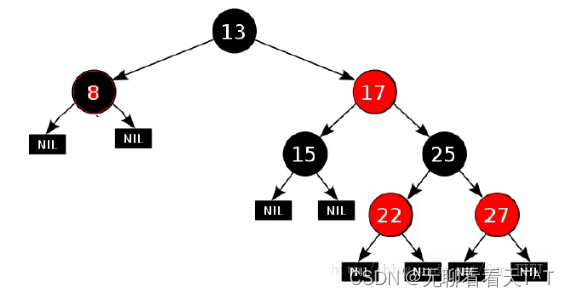
插入结点的颜色
问题:插入结点时还可以依据二叉搜索树的插入规则吗?插入结点应该都是什么颜色?
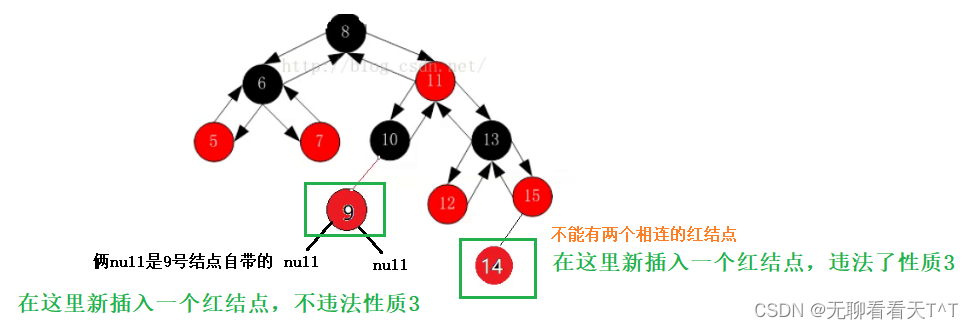
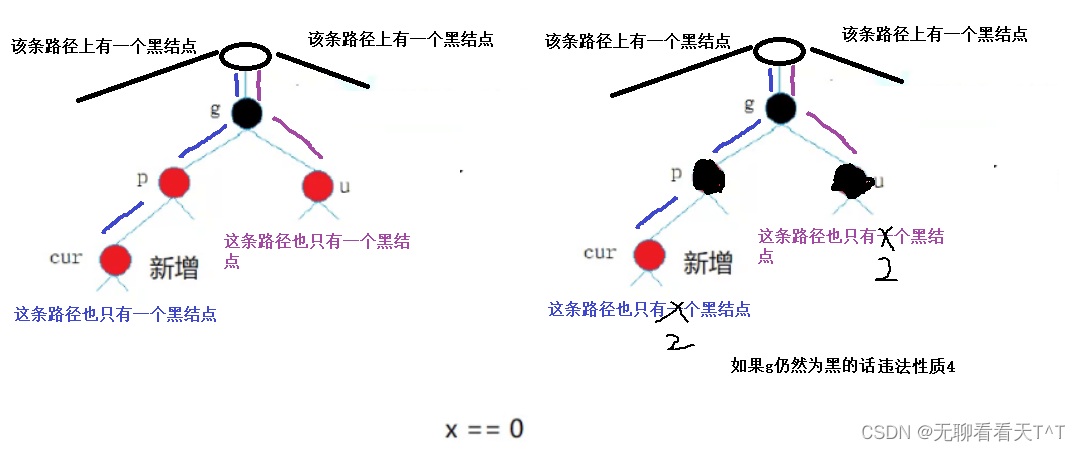
解释:可以且新插入的结点应该都是红色,因为插入结点的颜色是红色那么你只是可能违反性质3(如果一个结点是红色,则它的两个孩子结点都是黑色):
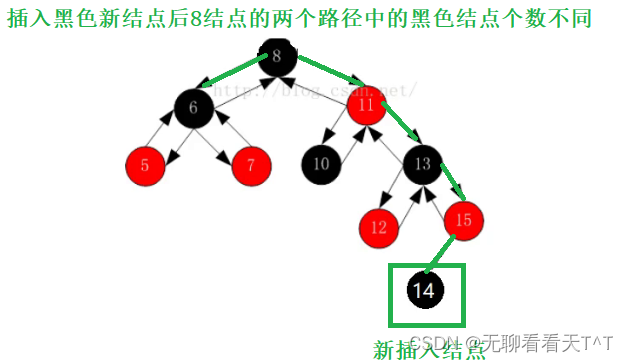
但是如果插入结点的颜色是黑色则一定违法性质4(对于每个结点,该结点到其所有后代叶子结点的简单路径上,均包含相同数目的黑色结点):
判断性质是否破坏
规定cur表示新插入结点,p表示父结点(parent)、g表示爷爷结点(grandfather)、u表示叔叔结点(uncle)
问题:如何确认在插入新结点后,红黑树的性质是否被破坏?
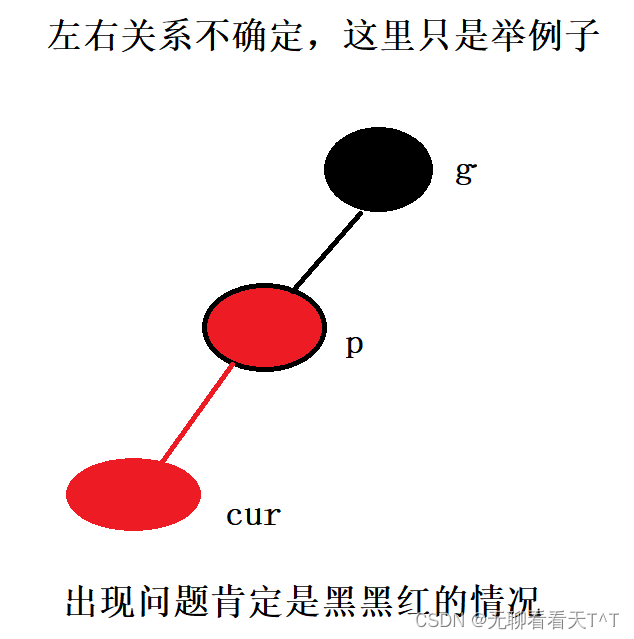
解释:新结点的颜色为红色,如果新结点的父结点颜色为红色,则违法性质3,需要进行调整
补充:p一定为红,g一定为黑,因为新插入结点的颜色是红色,插入该结点导致需要调整只可能是因为该结点的插入导致性质3遭到了破坏,那么p结点一定为红,而g也肯定为黑,因为在新插入结点前整颗红黑树应该是没有错误的(跟AVL树旋转是一个道理)
调整方式
问题:发现红黑树性质被破坏后,如何进行调整?(后面还有更准确的划分)
①由上述内容可知,在性质被破坏时cur一定为红、p一定为红、g一定为黑,那么关键点就在于p的兄弟结点u,对u的关注点应该在于它的“位置 + 存在情况”
②u的位置:p为g的左孩子,u就是g的右孩子,p为g的右孩子,u就是g的左孩子
③u的存在情况:u存在且为黑色,u存在且为红色、u不存在
u为g的右孩子
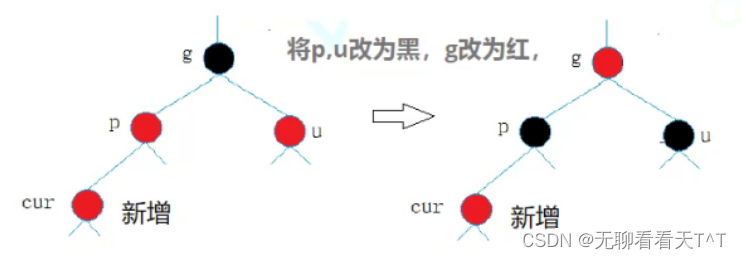
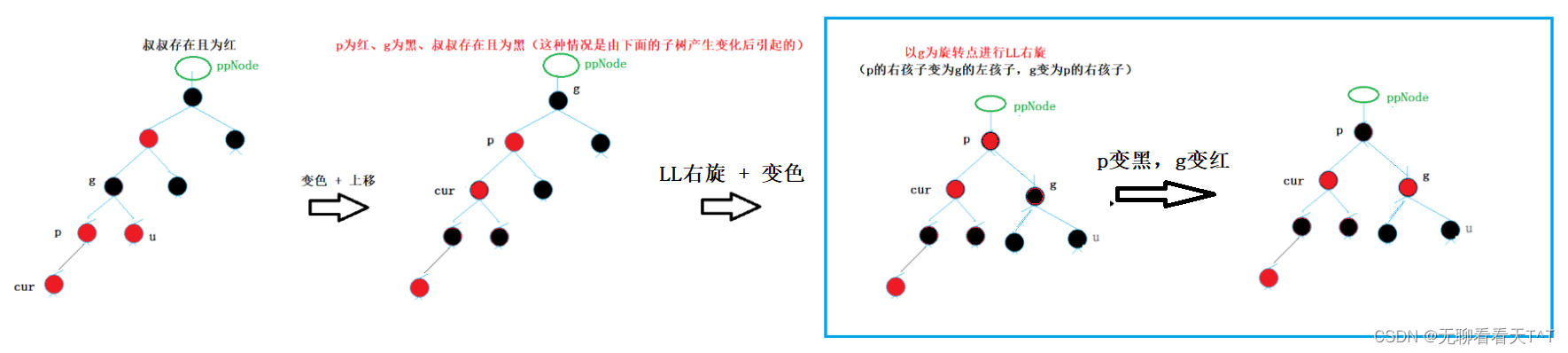
u存在且为红
解决办法:将p和u变为黑,g变为红(p和u替代了g保证路径上黑色结点数量不变)
遗留问题:
- 如果g是根结点,那么在g变红后为了满足性质2,仅需要将g重新变为黑色即可
- 如果g不是根结点,那么在g变红且g的父结点的颜色是黑色时,不需要继续向上调整
- 如果g不是根结点,那么在g变红且g的父结点的颜色是红色时,就需要继续向上调整
注意事项:
1、不能在发现新插入结点导致违法性质3后将cur再变为黑,因为那样还不如规定插入结点的颜色为黑色但是那样又一定会违法性质4
2、p和u改变后不能让g仍然为黑,因为如果g不是根结点,那么也会违法性质4
关于cur:无论cur是p的左孩子还是右孩子,当u存在且为红时,调整时只需要调色即可
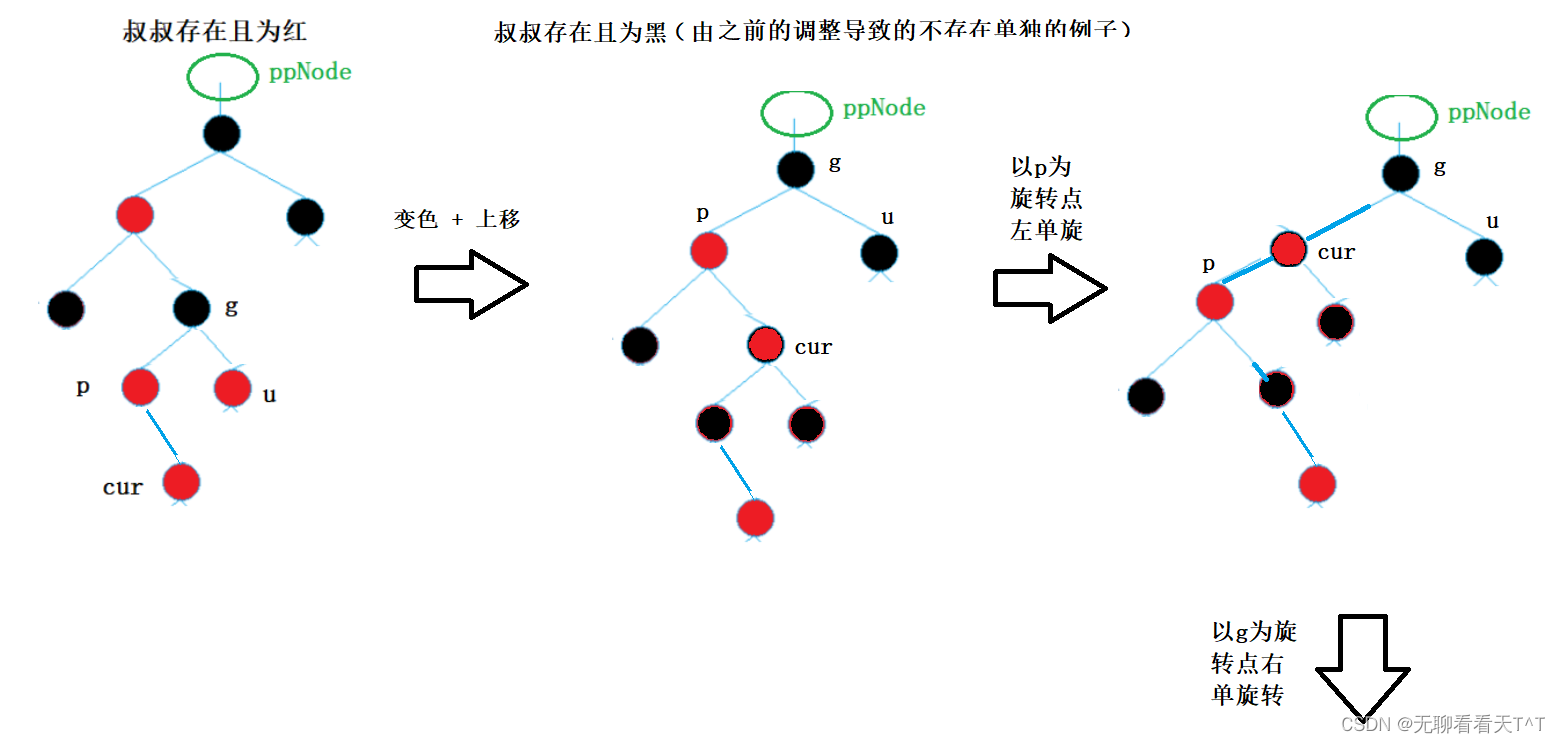
u存在且为黑
补充:下图演示的是u存在且为红在调整后,向上调节时遇到的u存在且为黑的情况,用一个例子将u存在且为红 + 向上调整 + u存在且为黑的情况都总结了
解决办法:先旋转(以g为旋转点进行LL右单旋),后变色(p变为黑,g变为红)
关于cur:
①上面的cur是p左孩子则以g为旋转点进行LL右单旋,p变黑g变红
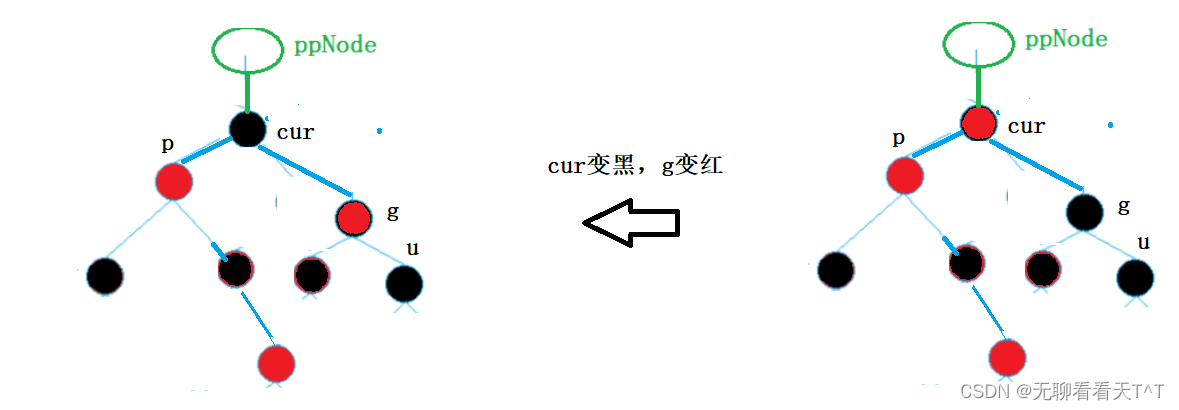
②若cur是p的右孩子先以p为旋转点进行左单旋,后以g为旋转点进行右单旋,cur变黑g变红
(颜色改变没有先后顺序,只要发生改变即可,先旋转后变色只是为了理解变色原因)
u不存在
解决办法:先变色(p变为黑,g变为红),后旋转(以g为旋转点进行LL右单旋)
关于cur:
①上面的cur是p左孩子则以g为旋转点进行LL右单旋,p变黑g变红
②若cur是p的右孩子先以p为旋转点进行左单旋,后以g为旋转点进行右单旋,cur变黑g变红
(颜色改变没有先后顺序,只要发生改变即可,先旋转后变色只是为了理解变色原因)
u为g的右孩子的情况不再分析,通过最终代码自己画图感受,主要区别在于旋转方式的不同
结论
- 每一次的调整都可能导致另一次红黑树性质的被破坏
- cur和parent均为红色是由“新增”或“向上调整”两种原因导致的,因此无论是这两种的哪一种,只有当cur和parent均不为红时才不需要继续调整(循环)
- 红黑树是否调整取决于cur和parent是否均为红,怎么调整取决于叔叔u的情况 + cur是p的哪个孩子
红黑树结点定义
// 结点颜色
enum Color
{ RED, BLACK
};// 红黑树节点的定义
template<class ValueType>
struct RBTreeNode
{RBTreeNode(const ValueType & data = ValueType(),Color color = RED): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _color(color){}RBTreeNode<ValueType>* _pLeft; // 节点的左孩子RBTreeNode<ValueType>* _pRight; // 节点的右孩子RBTreeNode<ValueType>* _pParent; // 节点的双亲ValueType _data; // 节点的值域 Color _color; // 节点的颜色
};- 演示的内容与最终代码中变量的名字存在区别
代码实现
#pragma once#include <iostream>
#include<vector>using namespace std;enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//规定插入的根结点颜色为黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED; // 规定新增节点的颜色是红色if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 当parent指向的结点不为空,且parent指向的结点的颜色不为黑色就继续向上调整(因为cur和parent均为红可能是由新增和向上调整导致的,因此无论是这两种情况的哪一种,// 只有当cur和parent均不为红时才结束循环)while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//通过父亲找到爷爷,父亲的父亲信息是爷爷//红黑树的关键点在于判断叔叔的情况if (parent == grandfather->_left)//如果父亲是爷爷的左孩子,那么叔叔就只能是爷爷的右孩子//这里if中的叔叔一直都是爷爷的右孩子,不过还会存在为红、为黑、不存在的三种情况{Node* uncle = grandfather->_right;// 如果叔叔存在且叔叔的颜色是红色,则直接将叔叔和父亲的颜色都变为黑色,将爷爷的颜色变为红色if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 防止修改颜色导致上方出现新的两个连续的红色结点,需要移动指针继续向上处理cur = grandfather;//cur指向爷爷结点parent = cur->_parent;//parent指向的是cur的父结点(cur向上走,parent也要向上走)}else // 叔叔不存在,或者存在且为黑{if (cur == parent->_left)//如果cur是父亲的左孩子,进行LL右单,旋转后将父亲的颜色变为黑,将爷爷的颜色变为红{// g // p u// c RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g // p u// c RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//如果父亲结点是爷爷结点的右孩子,那么叔叔结点就是爷爷结点的左孩子{Node* uncle = grandfather->_left;// 叔叔存在且为红,-》变色即可if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else // 叔叔不存在,或者存在且为黑{// 情况二:叔叔不存在或者存在且为黑// 旋转+变色// g// u p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;//不管最后整棵红黑树的根结点是什么颜色(因为向上调整可能会导致根结点颜色变为红色,也有可能根结点也颜色不变)//我们这里都直接重新将根结点的颜色设置为黑色,这样就不需要再在循环中去判断是否到达根结点return true;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_right == parent){ppNode->_right = subR;}else{ppNode->_left = subR;}subR->_parent = ppNode;}}//对用户暴露的中序遍历红黑树接口void InOrder(){_InOrder(_root);cout << endl;}//判断红黑树是否平衡bool IsBalance(){//首先根结点颜色得为黑if (_root->_col == RED){return false;}int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}private:bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){//cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色节点的数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}private:Node* _root = nullptr;
};//测试红黑树能否正常使用
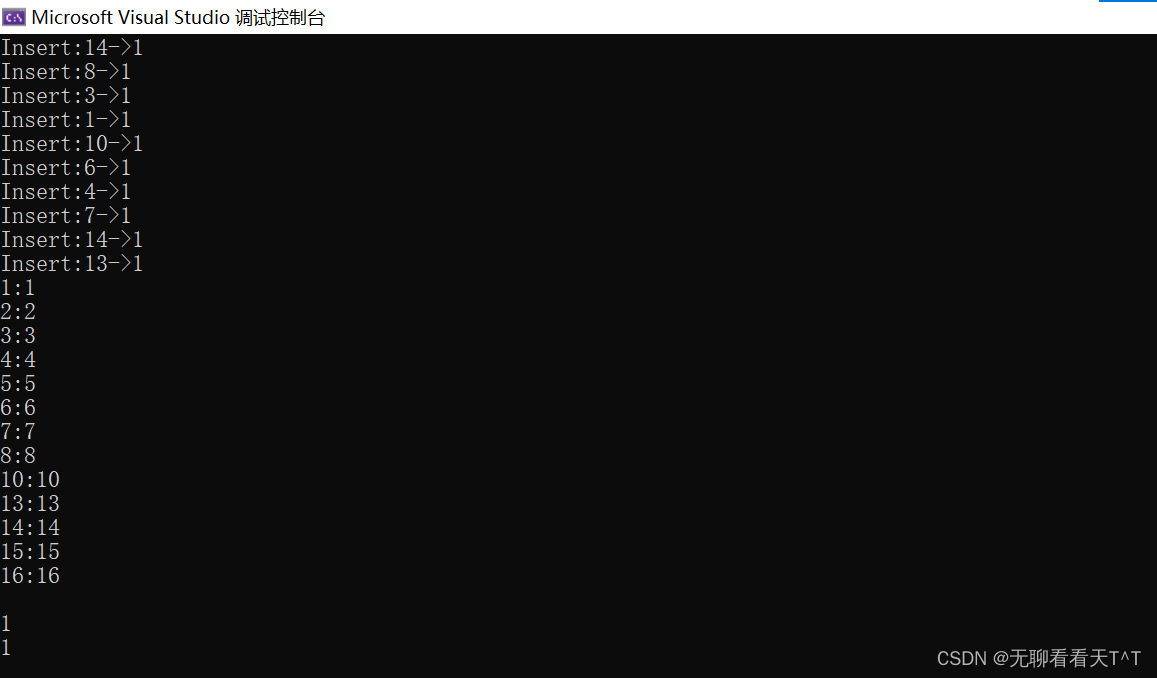
void TestRBTree1()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14,8, 3, 1, 10, 6, 4, 7, 14, 13 };RBTree<int, int> t1;for (auto e : a){if (e == 10){int i = 0;}// 1、先看是插入谁导致出现的问题// 2、打条件断点,画出插入前的树// 3、单步跟踪,对比图一一分析细节原因t1.Insert({e,e});std::cout << "Insert:" << e << "->" << t1.IsBalance() << std::endl;}t1.InOrder();std::cout << t1.IsBalance() << std::endl;
}//测试红黑树对百万数据处理所需时间
void TestRBTree2()
{const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);//cout << v.back() << endl;}size_t begin2 = clock();RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));//cout << "Insert:" << e << "->" << t.IsBalance() << endl;}size_t end2 = clock();std::cout << t.IsBalance() << std::endl;
}
~over~
相关文章:

C++的红黑树
目录 基本概念 插入结点的颜色 判断性质是否破坏 调整方式 u为g的右孩子 u存在且为红 u存在且为黑 u不存在 结论 红黑树结点定义 代码实现 基本概念 1、红黑树是一种特殊的二叉搜索树,每个结点会增加一个存储位表示结点的颜色(红或黑&#x…...

Keras深度学习框架第二十九讲:在自定义训练循环中应用KerasTuner超参数优化
1、简介 在KerasTuner中,HyperModel类提供了一种方便的方式来在可重用对象中定义搜索空间。你可以通过重写HyperModel.build()方法来定义和进行模型的超参数调优。为了对训练过程进行超参数调优(例如,通过选择适当的批处理大小、训练轮数或数…...

手机App收集个人信息,用户是否有权拒绝?
其实过度收集个人信息这件事,在APP上随处可见,泛滥成灾。 前两天有个不疼不痒的小软件“小鸡词典”,因为收集个人信息受到了处罚。 小鸡词典因划分为工具类APP过度收集隐私(手机号、地理位置定位)、不同意政策不能用…...

云下到云上,丽迅物流如何实现数据库降本50% | OceanBase案例
在2024年3月20日的首场OceanBase数据库城市行活动中,专注于物流及供应链解决方案的丽迅物流的架构师阳磊,围绕“OB Cloud在丽迅物流的实践”这一主题,进行了精彩的演讲。本文为此次演讲的内容回顾。 在丽迅物流(Lesoon Logistics…...

STM32无源蜂鸣器播放音乐
开发板:野火霸天虎V2 单片机:STM32F407ZGT6 开发软件:MDKSTM32CubeMX 文章目录 前言一、找一篇音乐的简谱二、确定音调三、确定节拍四、使用STM32CubeMX生成初始化代码五、代码分析 前言 本实验使用的是低电平触发的无源蜂鸣器 无源蜂鸣器是…...

【云原生】kubernetes中的认证、权限设置---RBAC授权原理分析与应用实战
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

【Python设计模式04】策略模式
策略模式(Strategy Pattern)是一种行为型设计模式,它定义了一系列算法,并将每个算法封装起来,使它们可以互相替换。策略模式让算法的变化不会影响使用算法的客户端,使得算法可以独立于客户端的变化而变化。…...

私域用户画像分析:你必须知道的3个关键点!
在互联网时代的变革中,私域流量成为越来越多企业的关注焦点。而了解私域用户画像是建立精准营销策略的关键一步。 今天,就给大家分享私域用户画像分析的三个关键点,让大家都能更好地进行用户画像分析。 1、市场需求 理解市场需求是把握用户…...
【MATLAB源码-第74期】基于matlab的OFDM-IM索引调制系统不同频偏误码率对比,对比OFDM系统。
操作环境: MATLAB 2022a 1、算法描述 OFDM-IM索引调制技术是一种新型的无线通信技术,它将正交频分复用(OFDM)和索引调制(IM)相结合,以提高频谱效率和系统容量。OFDM-IM索引调制技术的基本思想…...

优于其他超导量子比特数千倍!猫态量子比特实现超过十秒的受控比特翻转时间
内容来源:量子前哨(ID:Qforepost) 文丨娴睿/慕一 排版丨沛贤 深度好文:2000字丨8分钟阅读 摘要:量子计算公司Alice & Bob和QUANTIC团队(国立巴黎高等矿业学院PSL分校、巴黎高等师范学院和…...
QtXlsx库编译使用
文章目录 一、前言二、Windows编译使用2.1 用法①:QtXlsx作为Qt的附加模块2.1.1 检验是否安装Perl2.1.2 下载并解压QtXlsx源码2.1.3 MinGW 64-bit安装模块2.1.4 测试 2.2 用法②:直接使用源码 三、Linus编译使用3.1、安装Qt5开发软件包:qtbas…...

LeetCode题练习与总结:二叉树的层序遍历Ⅱ--107
一、题目描述 给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历) 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[…...
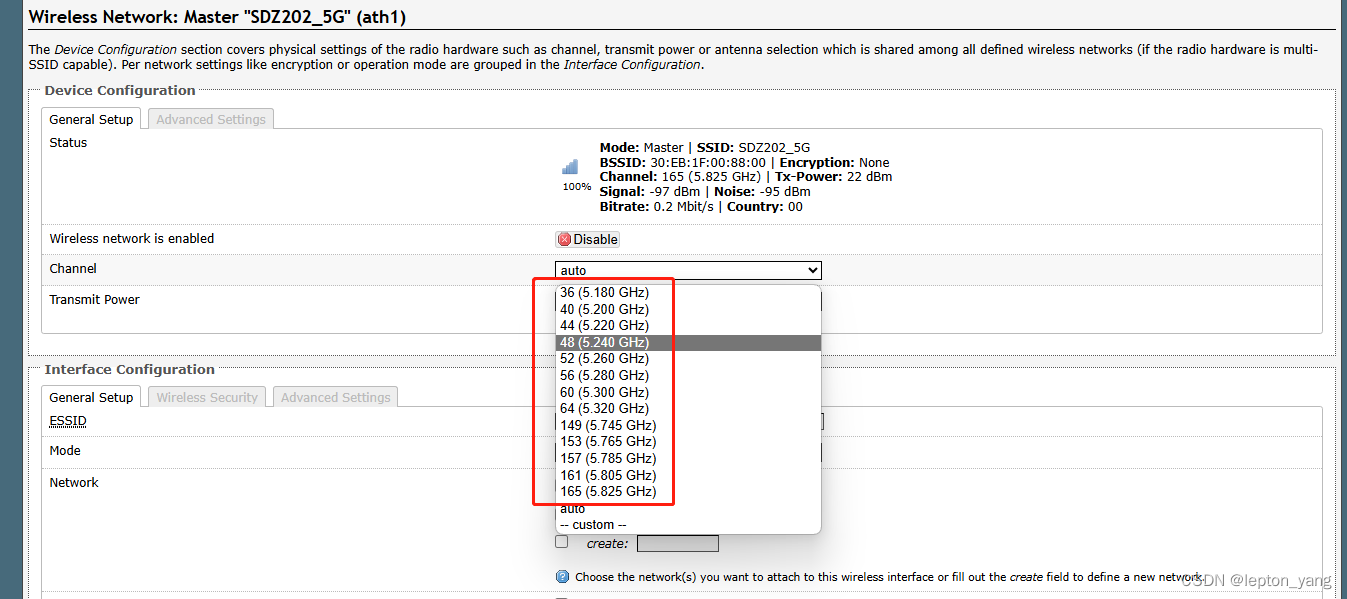
WIFI国家码设置的影响
记录下工作中关于国家码设置对WIFI的影响,以SKYLAB的SKW99和SDZ202模组为例进行说明。对应到日常,就是我们经常提及手机是“美版”“港版”等,它们的wifi国家码是不同的,各版本在wifi使用中遇到的各种情况与下面所述是吻合的。 现…...

2024年软考高项-信息系统管理师介绍-备考-考试内容-通过攻略
介绍 以下是计算机软件考试的资格设置,本文说的是高级资格中的信息系统项目管理师(简称"高项"),是比较热门和好考的选择,与中级的"系统集成项目管理工程师"有大部分的知识重叠交叉,中级考了"系统集成项…...

Python知识点复习
文章目录 Input & OutputVariables & Data typesPython字符串重复(字符串乘法)字符串和数字连接在一起print时,要强制类型转换int为str用input()得到的用户输入,是str类型,如果要以int形式计算的话,…...
GeoScene产品学习视频收集
1、易智瑞运营的极思课堂https://www.geosceneonline.cn/learn/library 2、历年易智瑞技术公开课视频资料 链接:技术公开课-易智瑞信息技术有限公司,GIS/地理信息系统,空间分析-制图-位置智能-地图 3、一些关于GeoScene系列产品和技术操作的视…...

51单片机的最小系统详解
51单片机的最小系统详解 1. 引言 在嵌入式系统中,51单片机被广泛应用于各种小型控制器和嵌入式开发板中。相信很多人都接触过51单片机,但是对于51单片机的最小系统却了解得不够深入。本文将从振荡电路、电源模块、复位电路、LED指示灯和调试接口五个方面详细介绍51单片机的…...

路径规划搜路算法有哪些?
路径规划搜索算法是帮助移动机器人或自动化系统在环境中从起点导航至终点的计算方法。以下是一些常见的路径规划搜索算法: Dijkstra算法:一种经典的最短路径搜索算法,适用于没有负权边的图。 A*算法:一种启发式搜索算法ÿ…...

Hadoop学习之hdfs的操作
Hadoop学习之hdfs的操作 1.将HDFS中的文件复制到本地 package com.shujia.hdfs;import org.apache.hadoop.conf.Configuration; import org.apache.hadoop.fs.FileSystem; import org.apache.hadoop.fs.Path; import org.junit.After; import org.junit.Before; import org.j…...

DBAPI怎么进行数据格式转换
DBAPI如何进行数据格式的转换 假设现在有个API,根据学生id查询学生信息,访问API查看数据格式如下 {"data":[{"name":"Michale","phone_number":null,"id":77,"age":55}],"msg"…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...