Leetcode 2028
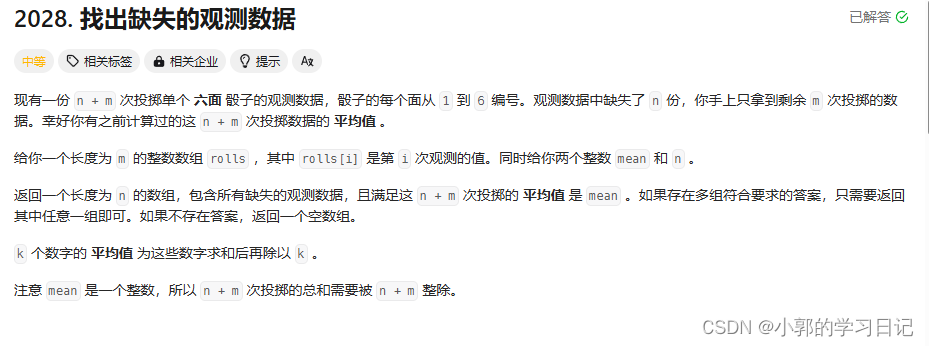

思路:1-6之间的的n个数组合起来要变成sum_t = mean*(rolls.size()+n) - sum(rolls) ;
那么可以先假设每个数都是sum_t / n 其中这个数必须要在1 - 6 之间否者无法分配。
然后可以得出n * (sum_t / n ) <= sum ; 需要对余数mod进行调整,为了减少调整的次数,每次尽量向上调整;最终调整完之后 mod 必须为0;
code:
class Solution {
public:vector<int> missingRolls(vector<int>& rolls, int mean, int n) {int len = rolls.size();int sum = (n + len) * mean;for(int i = 0 ; i < len; i++){sum -= rolls[i];}//从1-6找出n个数,求和等于sumif(sum / n > 6 || sum / n < 1)return {};//为答案数组分配结果, n * (sum / n) <= sum , vector<int> ans(n, sum / n);int mod = sum % n; //多余的部分,对答案进行调整,如果ans[i]小于6就可以进行一次调整,直到消除这个modint i = 0;while(mod && i < n){if(ans[i] < 6){if(6 - ans[i] >= mod){ans[i] += mod;mod = 0;}else{mod -= (6 - ans[i]);ans[i] = 6;}}i++;}if(mod != 0)return {};return ans;}
};相关文章:

Leetcode 2028
思路:1-6之间的的n个数组合起来要变成sum_t mean*(rolls.size()n) - sum(rolls) ; 那么可以先假设每个数都是sum_t / n 其中这个数必须要在1 - 6 之间否者无法分配。 然后可以得出n * (sum_t / n ) < sum ; 需要对余数mod进行调整,为了减少调整的次…...
Angular(1):使用Angular CLI创建空项目
要创建一个空的 Angular 项目,可以使用 Angular CLI(命令行界面)。以下是使用 Angular CLI 创建一个新项目的步骤: 1、安装 Angular CLI: 打开你的命令行界面(在 Windows 上是 CMD、PowerShell 或 Git Bas…...
算法原题)
字节跳动(校招)算法原题
大模型"价格战"越演越烈 昨天的 文章 提到,自从 5 月 15 号,字节跳动发布了击穿行业底价的豆包大模型后,各大厂家纷纷跟进降价,而且都不是普通降价,要么降价 90% 以上,要么直接免费。 今天是豆包…...

前端面试题日常练-day39 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末。 1. 哪个jQuery方法用于设置元素的HTML内容? a) .html() b) .text() c) .val() d) .append() 2. 在jQuery中,以下哪个方法用于隐藏或显示一个元素? a) .toggle…...
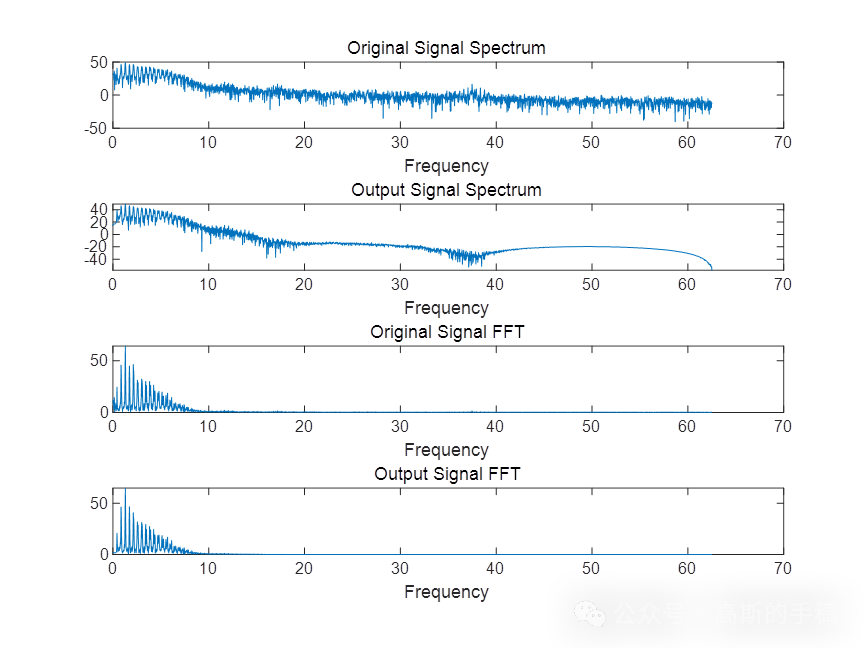
心电信号降噪方法(滤波器/移动平均/小波等,MATLAB环境)
对于一个正常的、完整的心动周期,对应的心电图波形如下图所示,各个波形都对应着心脏兴奋活动的生理过程,包含P波,PR段,QRS波群,ST段,T波,U波。 (1)P波心电图中…...

Kubernetes 文档 / 概念 / 工作负载 / 管理工作负载
Kubernetes 文档 / 概念 / 工作负载 / 管理工作负载 此文档从 Kubernetes 官网摘录 中文地址 英文地址 你已经部署了你的应用并且通过 Service 将其暴露出来。现在要做什么? Kubernetes 提供了一系列的工具帮助你管理应用的部署,包括扩缩和更新。 组织…...

【第6章】SpringBoot整合Mybatis
文章目录 前言一、准备1. 版本要求2.安装3. 建表语句 二、案例1. mapper2.实体类3.测试类4.扫描5. 配置6. mapper.xml7.输出 总结 前言 MyBatis-Spring-Boot-Starter 可以帮助你更快地在 Spring Boot 之上构建 MyBatis 应用。 一、准备 1. 版本要求 MyBatis-Spring-Boot-Sta…...

vim常用指令——001
vim常用指令 Vim的命令模式常用操作一、定位移动光标二、行的基本操作【复制、粘贴、删除】三、查找、替换四、分屏命令 总结给大家总结下四个运行模式: Vim的命令模式常用操作 一、定位移动光标 按h:将光标向左移动一个字符,等同于方向键左…...
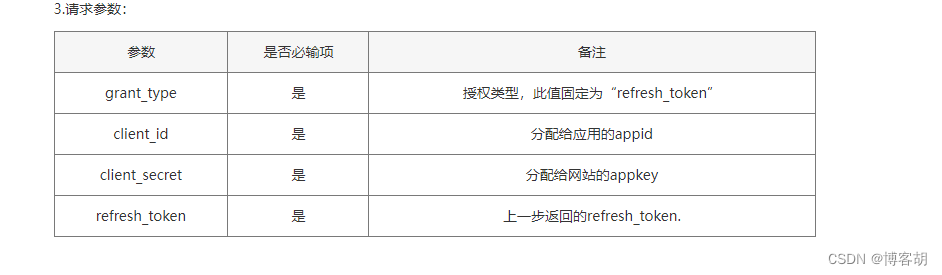
java 对接农行支付相关业务(二)
文章目录 农行掌银集成第三方APP1:掌银支付对接快e通的流程1.1 在农行网站上注册我们的app信息([网址](https://openbank.abchina.com/Portal/index/index.html))1.2:java整合农行的jar包依赖1.3:把相关配置信息整合到项目中1.4:前端获取授权码信息1.5:后端根据授权码信…...
超频是什么意思?超频的好处和坏处
你是否曾经听说过超频?在电脑爱好者的圈子里,这个词似乎非常熟悉,但对很多普通用户来说,它可能还是一个神秘而陌生的存在。 电脑超频是什么意思 电脑超频(Overclocking),顾名思义,是…...

【cocos creator】进度条控制脚本,支持节点进度条,图片进度条,进度条组件,和进度文字展示
进度条控制脚本,支持节点进度条,图片进度条,进度条组件,和进度文字展示 const { ccclass, property, menu } cc._decorator;let text_type cc.Enum({"20%": 0,"1/5": 1,"差值": 2,"自定义…...

Bean的一些属性信息总结
我们知道,在Spring中,一个Bean可以理解为一个对象,但是二者之间肯定是有区别的,比如一个Bean可以实例化成很多个对象、Bean中可以带有某些描述信息。 学习Bean,能更好地使用Bean。 1、Spring两个核心概念的由来【可忽…...

CentOS 7 安装 Minio
获取MinIO安装包 下载地址如下:下载地址通过以下命令可直接将安装包下载至服务器 wget https://dl.min.io/server/minio/release/linux-amd64/archive/minio-20230809233022.0.0.x86_64.rpm安装MinIO rpm -ivh minio-20230809233022.0.0.x86_64.rpm集成Systemd …...
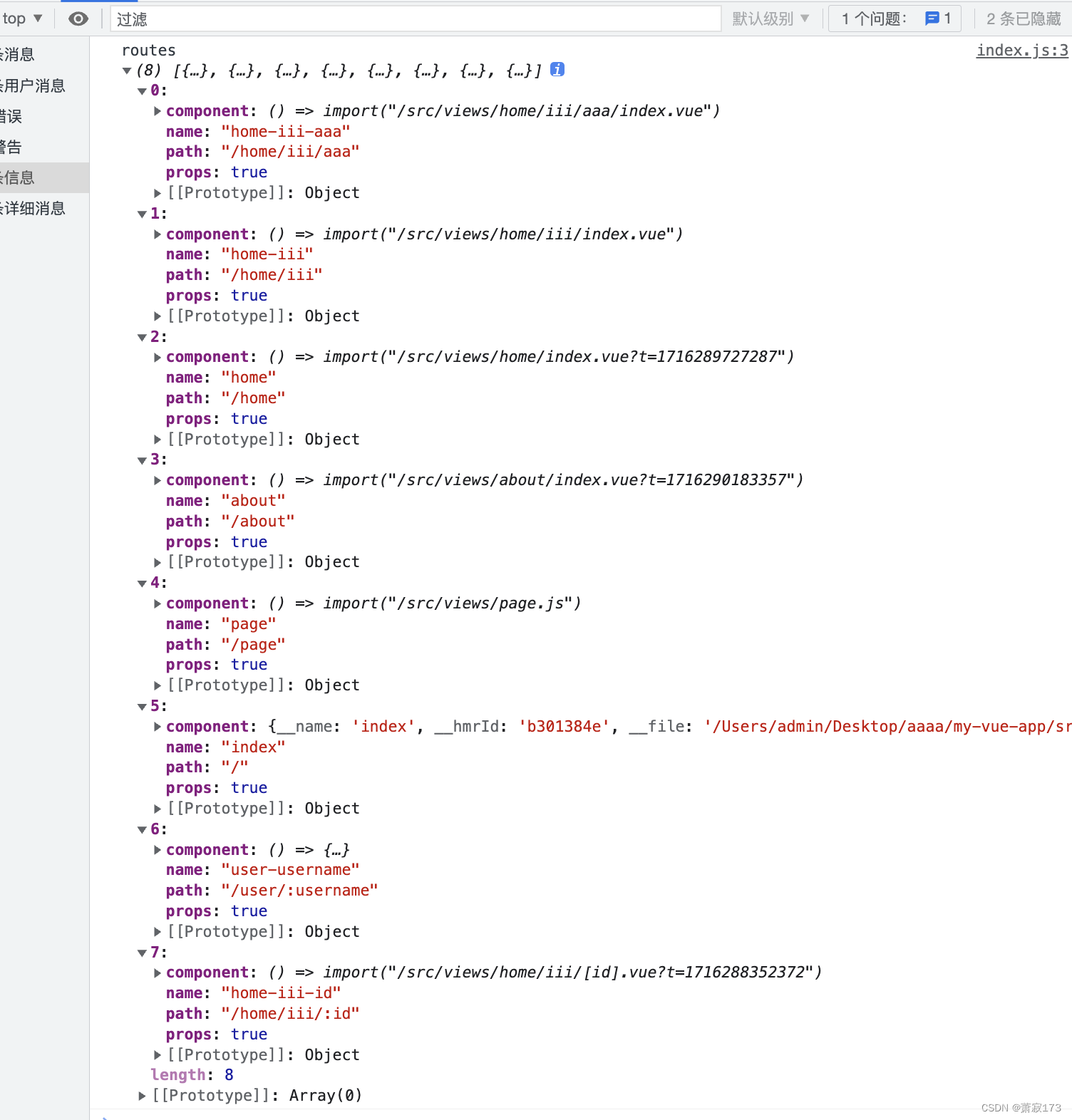
vue3和vite实现vue-router4版本路由的配置以及自动生成路由配置
这个是普通的手动路由配置:https://blog.csdn.net/weixin_68658847/article/details/130071101 自动路由配置 创建项目 npm create vitelatest my-vue-app -- --template vue // 或者 yarn create vite my-vue-app --template vue// 安装路由 yarn add vue-route…...

Flutter 中的 CupertinoDatePicker 小部件:全面指南
Flutter 中的 CupertinoDatePicker 小部件:全面指南 在 Flutter 中,CupertinoDatePicker 是 Cupertino 组件库的一部分,它提供了一个 iOS 风格的日期选择器。这个选择器允许用户选择日期和时间,非常适合需要符合 iOS 设计指南的应…...

用 Python 编写自动发送每日电子邮件报告的脚本
第一步:安装必要的库 你需要安装 smtplib(Python 自带),但你需要安装 schedule 和 email 库。你可以使用以下命令安装这些库: pip install schedule第二步:编写发送邮件的脚本 这里是一个完整的 Python …...

IT人的拖延——渴望成功与害怕成功的矛盾
很多人都以为,害怕失败是拖延的主要诱因,但其实“害怕成功”也是拖延的主要诱因之一。要说这个原因,我们不得不提起Bible中的一个人“约拿”,让我们先来看看他的故事带给我们什么启示。 约拿情结简介 约拿是Bible中的一名先知&a…...

【全开源】场馆预定系统源码(ThinkPHP+FastAdmin+UniApp)
一款基于ThinkPHPFastAdminUniApp开发的多场馆场地预定小程序,提供运动场馆运营解决方案,适用于体育馆、羽毛球馆、兵乒球馆、篮球馆、网球馆等场馆。 场馆预定系统源码:打造高效便捷的预定体验 一、引言:数字化预定时代的来临 …...
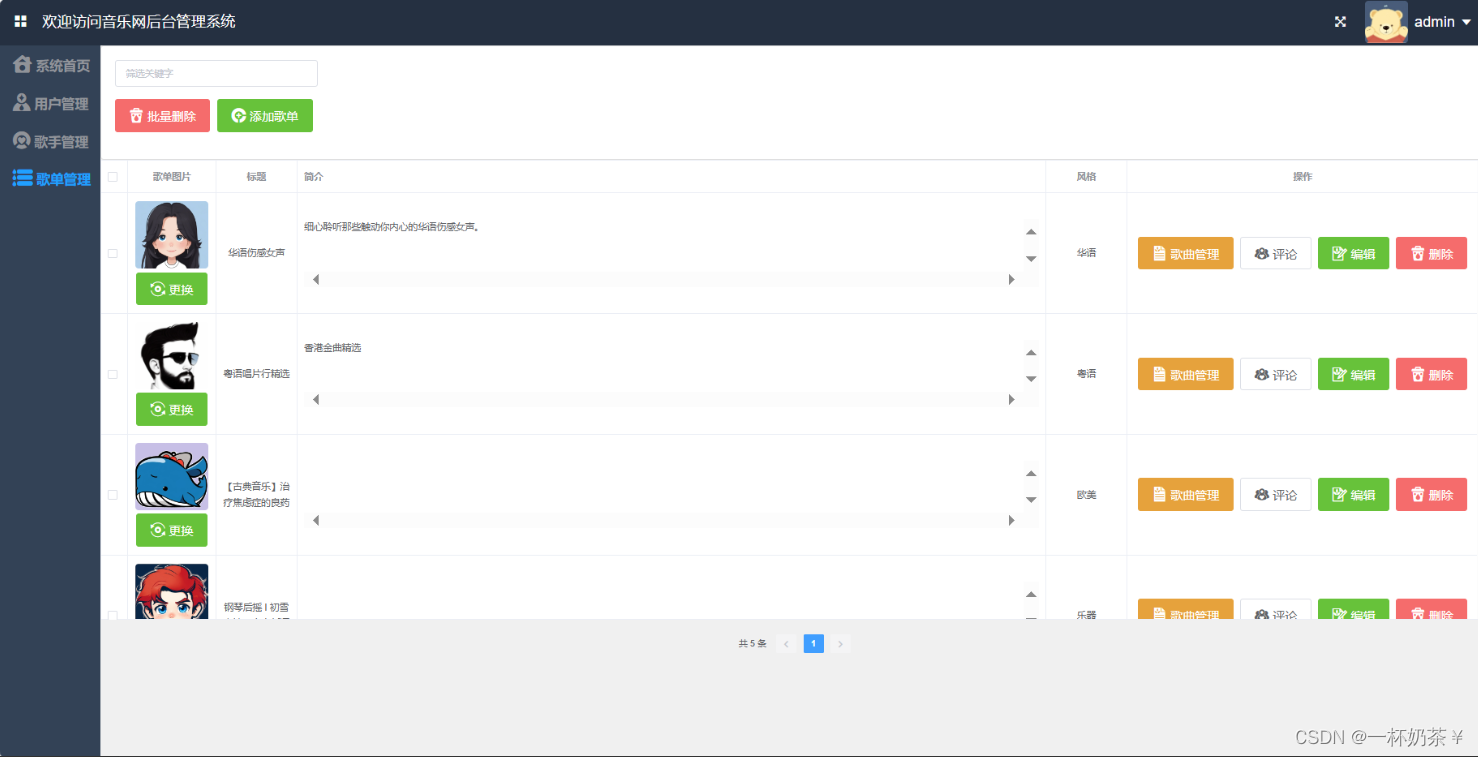
音乐系统java在线音乐网站基于springboot+vue的音乐系统带万字文档
文章目录 音乐系统一、项目演示二、项目介绍三、万字项目文档四、部分功能截图五、部分代码展示六、底部获取项目源码和万字论文参考(9.9¥带走) 音乐系统 一、项目演示 在线音乐系统 二、项目介绍 基于springbootvue的前后端分离在线音乐系…...
)
Python—面向对象小解(1)
一、面向对象 面向对象编程(Object-Oriented Programming,简称 OOP)是一种程序设计范式,它通过使用“对象”和“类”来组织代码。Python 是一种面向对象的编程语言,支持 OOP 的核心概念。 面向过程:…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
