常见问题整理1
目录
偏差和方差
欠拟合underfitting
过拟合overfitting
梯度消失和梯度爆炸
归一化
偏差和方差
偏差:算法期望预测和真实预测之间的偏差程度。反应的是模型本身的拟合能力。
方差:度量了同等大小的训练集的变动导致学习性能的变化,刻画了数据扰动导致的影响。
欠拟合underfitting
解决措施:
1.添加其他特征项(增大数据量)
2.添加多项式特征(增加网络层数,用更加复杂得模型)
3.减少正则化参数
过拟合overfitting
解决措施:
1.重新清洗数据
2.增大数据的训练量
3.采用正则化方法
4.采用dropout方法
Vanilla dropout:训练时使用概率p丢弃某些神经元,测试时,让最后输出乘以(1-p)来保证期望一致。
Inverted dropout:训练时使用概率p丢弃某些神经元,同时对该层的输出除以(1-p),这样的话就不需要再测试阶段引入了。
dropout有什么优点?有什么缺点?
优点:阻止某些特征的协同作用,减小方差,防止过拟合,增强鲁棒性。因为如果模型对某些特征过拟合的话,训练的时候通过dropout使得这些容易拟合的特征出现的概率降低,减小因这个输入变化带来的对模型的影响
缺点:会改变某些特征的分布,比如性别特征编码为{男->0,女->1},当以概率p将女随机变为0的话,在一定程度上增加了男得概率(0.5+0.5*p),这样得话就改变了性别特征得分布,最后测试阶段再通过乘以(1-p)并不能恢复原始数据分布;这个得解决方法是:上面这个例子应该从编码得角度解决,比如{男->1,女->2,未知->0}。
5.提前终止训练
6.减少网络层数,使用简单得模型
梯度消失和梯度爆炸
原理:
梯度消失:当网络层数很深时,如果梯度小于1,则会使得经过多层后向反馈时得梯度累乘远远小于1;
梯度爆炸:与梯度消失相反,当网络层数很深时,如果梯度大于1,则会使得经过多层后向反馈后得梯度累乘远远大于1;
解决措施:
1.激活函数得选择(使用Relu代替sigmoid,tanh等)
2.预训练+微调
3.使用batch normalization
公式:normalization(归一化)+scale-shift(反归一化)
gamma*(x-E[x])/(sqrt(VAR[x]+e))+beta,其中E[x]为mini-batch mean, VAR[x]为mini-batch variance
gamma(初始化为1)和beta(初始化为0)是可学习参数
为什么BN有效果?
1)因为BN主要是将映射后数据进行归一化,这样对于sigmoid函数或tanh函数来说,能够使得数据分布在梯度较大得区域,同时加速收敛。
2)由于BN中计算得是mini-batch mean和mini-batch variance,所以引入了一些noise,有一定正则作用
mini-batch mean和mini-batch variance会带来noise,那如何缓解呢?
训练过程中可以利用指数加权移动平均来累计mean和variance,这个得mean和variance接近all-batch
为什么BN归一化后还要有scale-shift操作?
这是利用神经网络自己去学习 归一化有没有效果,如果没有效果,则使用scale-shift操作来抵消归一化得作用。
BN改变了数据分布,为什么效果反而会更好?
1)虽然会改变数据分布,但是数据之间得关联性是不会变得。
2)由于有目标函数在,所以神经网络自己会朝着分布最优得方向去学习。
BN用在什么地方?
根据它起到得效果可知,一般用在全连接层+BN+激活函数
对于什么激活函数,BN效果更明显?
对于sigmoihe激活函数或者tanh激活函数,BN效果会好一些
BN中在训练和测试时怎么用?
训练中使用得是:计算每个mini-batch得数据
测试中使用得是:在训练过程中,通过指数加权移动平局来统计均值和方差,将这个值用于测试阶段计算。
BN缺点
1)小样本时,效果不好,均值和方差是有偏得
2)在RNN中效果通常不好--将不同batch得数据进行归一化,不符合句子内的语义更强的特点
BN和Dropout
Dropout为了平衡训练和测试的差异,会通过随机失活的概率来对神经元进行放缩,进而会改变其方差。如果再加一层BN,又将方差拉回至(0-1)分布,进而产生方差冲突。
处理方法:1.将dropout放在BN后;2.使用高斯dropout。
4.使用残差网络结构
5.使用LSTM网络
为什么LSTM比RNN更能解决梯度消失的问题?
因为在RNN中,BPTT的梯度是累乘形式,而RNN的输出中采用了tanh激活函数,所以会出现梯度消失问题;而LSTM的梯度除了累乘形式,还有累加形式,所以不容易出现梯度消失。
LSTM中用sigmoid激活函数,而不用ReLU激活函数的原因?
因为在LSTM中,忘记门和更新门是起筛选作用,所以需要0~1之间的至作为概率来进行筛选。
6.梯度剪切、权重正则
7.Layer normalization
公式:normalization(归一化)+scale-shift(反归一化)
gamma*(x-E[x])/(sqrt(VAR[x]+e))+beta,其中E[x]为mini-batch mean, VAR[x]为mini-batch variance
不需要额外维护一个对训练样本均值方差的统计,每次只需要在句子范围内计算即可
gamma(初始化为1)和beta(初始化为0)是可学习参数
归一化
机器学习为什么对数据进行归一化?
归一化的目的:
1.处理不同规模和量纲的数据,将其缩放到相同的数据区间和范围,以减少规模、特征、分布差异对模型的影响。
2.归一化加速GD求解最优解的速度。比如收敛路径呈Z字型,导致收敛太慢;
3.归一化可以提高精度。
机器学习什么情况下对数据进行归一化?
1.使用了梯度下降算法,如LR,SVM等。
2.计算样本点距离时,如KNN、K-Means等。
.....
机器学习什么情况下不需要归一化?
1.概率模型(决策树)不需要归一化
决策树不需要归一化:因为决策树分裂时是通过统计的方式寻找最优分裂点,并不是直接对数值进行拟合。
如何应用到训练集、测试集和验证集中?
由于测试集是未知的,所以测试集的归一化的均值和方差应该来源于训练集。验证集同理。
常用的归一化方法及适用情景
2.max-min法:容易受极端值的影响,一定程度上会破坏原有的数据结构;
3.z-score法:会改变原有数据的分布,不适合对稀疏数据做处理,不适合根据变量差异程度的聚类分析;

4.非线性归一化:log,exp,tanh,sigmoid等,取决于输入数据范围以及期望的输出范围。
5.length-one归一化:x/||x||这种处理用在不考虑向量大小而需要考虑向量方向的问题中,比如在一些文本情感的分类中,我们可能并不需要知道情感表达的强弱,而只要知道情感的类型,比如开心,生气等等。将特征转换为单位向量形式,可以剔除特征的强度的影响。
6.RobustScaler:适用于存在离群点的数据。
上述方法分析:在分类中,聚类算法,数据符合正态分布中,需要使用距离来度量相似性或者使用PCA降维时,z-score表现得较好。在不涉及距离测量,协方差计算,数据不太符合正态分布时,可以使用第一种方法或其他方法。
LR归一化问题,什么情况下可以不归一化,什么情况下必须归一化,为什么?
当数据分布比较集中时,可以不归一化
当数据分布比较分散时,需要归一化
相关文章:

常见问题整理1
目录 偏差和方差 欠拟合underfitting 过拟合overfitting 梯度消失和梯度爆炸 归一化 偏差和方差 偏差:算法期望预测和真实预测之间的偏差程度。反应的是模型本身的拟合能力。 方差:度量了同等大小的训练集的变动导致学习性能的变化,刻画…...
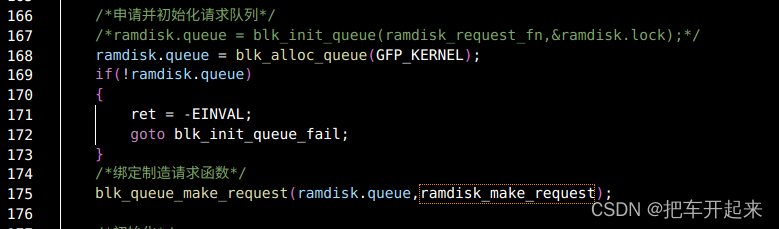
体验Linux 块设备驱动实验(模拟块)
目录 一、块设备 二、块设备驱动框架 1、块设备的注册和注销 2、gendisk 结构体 3、block_device_operations 结构体 4、块设备 I/O 请求过程 ①、请求队列 request_queue ②、bio 结构 三、编写驱动之请求队列 1、修改makefile 2、基本的驱动框架编辑 3、添加头文…...
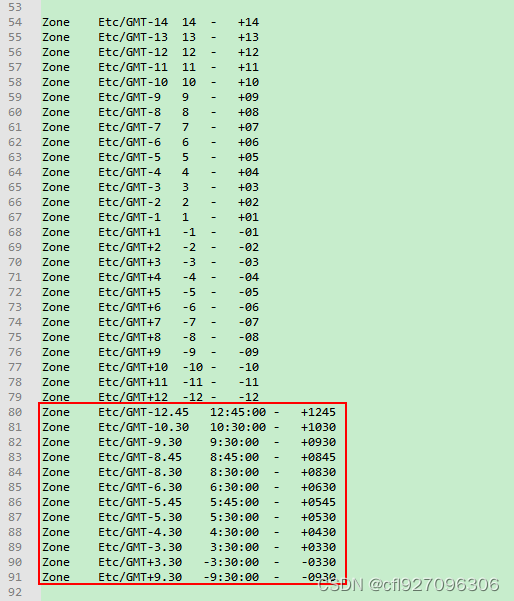
一文搞懂Linux时区设置、自定义时区文件
概念介绍 常说的 Linux 系统时钟有两个 一个是硬件时钟(RTC),即BIOS时间,一般保存的是 GMT0 时间,没时区、夏令时的概念 一个是当地时钟(LTC),即我们日常经常看到的时间࿰…...
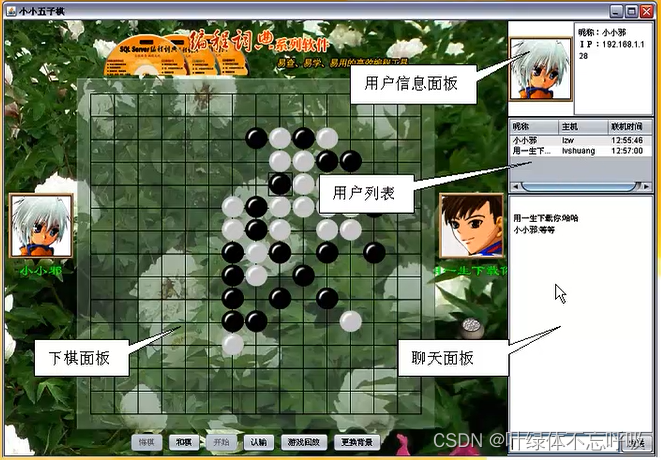
Java实例实验项目大全源码企业通讯打印系统计划酒店图书学生管理进销存商城门户网站五子棋
wx供重浩:创享日记 对话框发送:java实例 获取完整源码源文件视频讲解文档资料等 文章目录1、企业通讯2、快递打印系统3、开发计划管理系统4、酒店管理系统5、图书馆管理系统6、学生成绩管理系统7、进销存管理系统8、神奇Book——图书商城9、企业门户网站…...
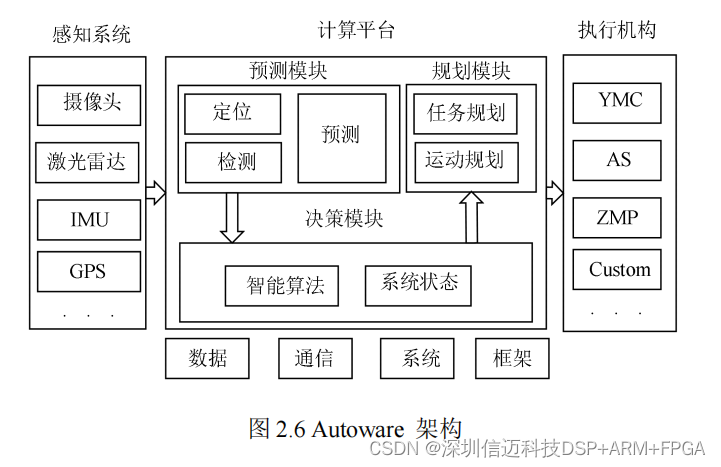
基于nvidia xavier智能车辆自动驾驶域控制器设计与实现-百度Apollo架构(二)
智能车辆操作系统 智能车辆操作系统是智能车辆系统的重要组成部分。现代汽车软件组件通常首 先由不同的供应商开发,然后在有限的资源下由制造商进行集成[42]。智能车辆操作 系统需要采用模块化和分层化设计思想来兼容传感器、分布式通信和自动驾驶通用 框架等模块&a…...
 网课笔记总结)
考研408 王道计算机考研 (初试/复试) 网课笔记总结
计算机初试、复试笔记总结(导航栏)📝 一、初试 408 408 - 1. 数据结构与算法 数据结构与算法 笔记导航🚥🚥🚥 🥬 第一章 绪论(无)🥕 第二章 线性表🥪 第三章 栈和队列&…...
[Java·算法·中等]LeetCode34. 在排序数组中查找元素的第一个和最后一个位置
每天一题,防止痴呆题目示例分析思路1题解1👉️ 力扣原文 题目 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1,…...
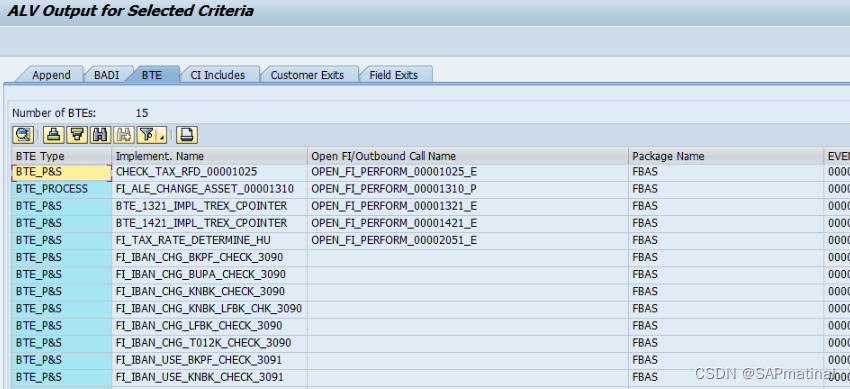
SAP BTEs的简介及实现
一、认识BTE BTE(Business Transaction Event)也称之为“业务交易事件”,一般的增强(Tcode:SMOD|CMOD)依旧使用ABAP进行二次开发,然而BTE则提供了RFC调用其它产品的可能(Tcode:FIBF)。BTE的设计思路更加简单,和BADI有点类似。在标准程序中留有…...

如何利用海外主机服务提高网站速度?
网站速度是任何在线业务成功的关键。快速的网站速度可以让用户更快地访问您的网站,增加页面浏览量。对于拥有全球用户的网站而言,选择一个海外主机服务商是提高网站速度的有效方法之一。下面是一些利用海外主机服务(如美国主机、香港主机)提高网站速度的…...

【SpringMVC】 一文掌握 》》》 @RequestMapping注解
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ RequestMapping注解一、SpringMVC环境准备1.相…...
高三应该怎么复习
高三是学生们备战高考的重要一年,正确有序的复习可以有效地提高复习效率,下面是一些高效复习的方法和建议:1. 制定合理的学习计划和目标高三的学生要制定合理的学习计划和目标,适当的计划和目标可以使学习更有针对性和效率。建议根…...
如何通过C++ 将数据写入 Excel 工作表
直观的界面、出色的计算功能和图表工具,使Excel成为了最流行的个人计算机数据处理软件。在独立的数据包含的信息量太少,而过多的数据又难以理清头绪时,制作成表格是数据管理的最有效手段之一。这样不仅可以方便整理数据,还可以方便…...

Kalman Filter in SLAM (6) ——Error-state Kalman Filter (EsKF, 误差状态卡尔曼滤波)
文章目录0.前言1. IMU的误差状态空间方程2. 误差状态观测方程3. 误差状态卡尔曼滤波4. 误差状态卡尔曼滤波方程细节问题0.前言 这里先说一句:什么误差状态卡尔曼?完全就是在扯淡! 回想上面我们推导的IMU的误差状态空间方程,其实…...
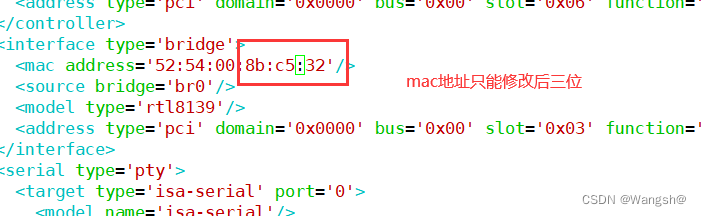
centos7部署KVM虚拟化
目录 centos7部署KVM虚拟化平台 1、新建一台虚拟机 2、系统内的操作 1、修改主机名 2、挂载镜像光盘 3、ssh优化 4、设置本地yum仓库 5、关闭防火墙,selinux 3、安装KVM 4、设置KVM网络 5、KVM部署与管理 6、使用虚拟系统管理器管理虚拟机 创建存储池 …...

【华为机试真题详解 Python实现】最小施肥机能效【2023 Q1 | 100分】
文章目录 前言题目描述输入描述输出描述示例 1输入:输出:示例 2输入:输出:题目解析参考代码暴力解法二分法前言 《华为机试真题详解》专栏含牛客网华为专栏、华为面经试题、华为OD机试真题。 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可…...
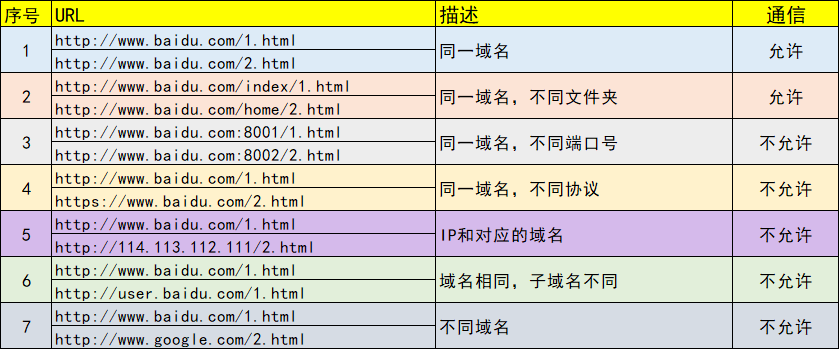
SpringBoot - 什么是跨域?如何解决跨域?
什么是跨域? 在浏览器上当前访问的网站,向另一个网站发送请求,用于获取数据的过程就是跨域请求。 跨域,是浏览器的同源策略决定的,是一个重要的浏览器安全策略,用于限制一个 origin 的文档或者它加载的脚本…...
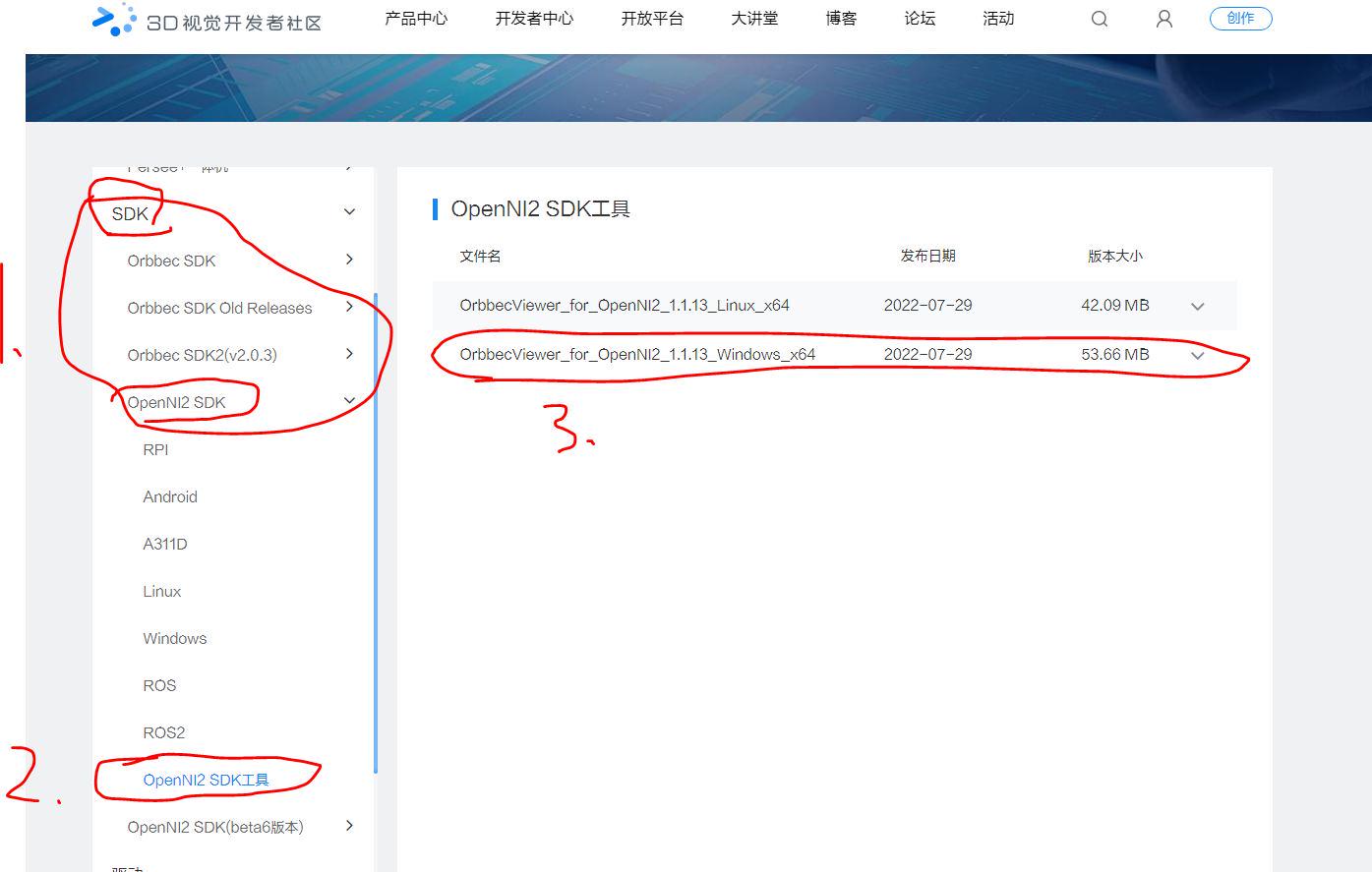
Astra pro相机使用说明
奥比中光的Astra pro这款相机,目前官网已经搜不到相关信息,应该是停产了。但是很多机器人设备上或者淘宝上还能买到。使用起来经常会出现不同的问题。问题1: 这款相机据网友描述,就是乐视相机LeTMC-520,换了外壳&#…...

扬帆优配|数字经济刮起“东风”,龙头晋级7连板
今日两市共40只涨停股,主要集中于数字经济、6G板块,上一个交易日涨停股为29股;除掉18只ST股及3只一字板新股,共19股涨停。另外,4股封板未遂,整体封板率为83%。 6股封单金额超亿元 从收盘涨停板封单量来看&…...

Day911.DTO和DO为什么要互转 -SpringBoot与K8s云原生微服务实践
DTO和DO为什么要互转 Hi,我是阿昌,今天学习记录的是关于DTO和DO为什么要互转的内容。 一、什么是DTO DTO ,数据传输对象,全称 (Data transfer object),用于网络之间传输通讯的对象模型&#x…...

查找、排序、二叉树的算法,统统记录于此。
文章目录一、查找1. 无序表的顺序查找2. 折半查找3. 分块查找4. 二叉排序树BST5. 哈希表查找二、排序1. 不带哨兵的直接插入排序2. 带哨兵的直接插入排序3. 带哨兵、折半查找的直接插入排序4. 希尔排序5. 冒泡排序6. 快速排序7. 选择排序8. 堆排序9. 归并排序二叉树1. 递归先序…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
