二分查找算法详讲(三种版本写法)原创
介绍:
二分查找算法(Binary Search)是一种在有序数组中查找目标元素的算法。
它的基本思想是通过将目标元素与数组的中间元素进行比较,从而将搜索范围缩小一半。
- 如果目标元素等于中间元素,则搜索结束;
- 如果目标元素小于中间元素,则继续在左半部分查找;
- 如果目标元素大于中间元素,则在右半部分查找。
通过不断地将搜索范围缩小一半,最终可以找到目标元素或确定目标元素不存在。
接下来通过例题介绍二分的不同写法
例题:
输入一个整数 n, 接下来一行输入 n 个整数(保证整数序列有序), 最后输入一个整数 m, 查找 m 在序列中的起始下标和结束下标
示例1:
输入:
5
1 2 2 4 5
2
输出:
1 2
解释:
2 在序列中的起始和结束位置是下标 1 和 2
代码讲解:
二分代码按照退出条件分为
- while (l <= r)
- while (l < r)
代码中的所有 l 和 r 都是序列的左右闭区间
代码中的所有 l + r >> 1 和 l + r + 1 >> 1 分别相当于 (l + r) / 2 和 (l + r + 1) / 2。>>是按位右移, 整数向右位移一位相当于除2
代码中的所有 x, 都是目标值, 也就是要查找的值; 所有的 idx, 是答案, 也就是要查找数的起始下标或结束下标
先讲第一种: while (l <= r), 在l > r时退出
// 查找起始下标
int l = 0, r = n - 1, idx = 0;
while (l <= r)
{int mid = l + r >> 1; // 一分为3, [l, mid), [mid, mid], (mid, r]if (a[mid] < x) l = mid + 1; // 如果当前中间值比 x 小, 需要去序列的右区间, 因为mid位置的数比 x 小, 那么左边的区间(l, mid]的所有数都比 x 小else if (a[mid] > x) r = mid - 1; // 同上else if (a[mid] == x) // 等于答案时{idx = mid;r = mid - 1; // 我们要找的时起始的下标, 虽然此时a[mid] == x, 但是mid的左边可能还有等于x的值, 所以我们要继续往左区间去找}
}// 查找结束下标(代码中只有注释的地方和上面的代码不一样)
int l = 0, r = n - 1, idx = 0;
while (l <= r)
{int mid = l + r >> 1; // 一分为3, [l, mid), [mid, mid], (mid, r]if (a[mid] < x) l = mid + 1; else if (a[mid] > x) r = mid - 1; else if (a[mid] == x) {idx = mid;l = mid + 1; // 我们要找的时结束的下标, 虽然此时a[mid] == x, 但是mid的右边可能还有等于x的值, 所以我们要继续往右区间去找}
}
观察上面代码我们可以把a[mid] == x的情况跟其他两种情况合并
// 查找起始下标
int l = 0, r = n - 1, idx = 0;
while (l <= r)
{int mid = l + r >> 1; // 一分为3, [l, mid), [mid, mid], (mid, r]if (a[mid] < x) l = mid + 1; else if (a[mid] >= x){idx = mid;r = mid - 1; // 继续往左区间找}
}// 查找结束下标
int l = 0, r = n - 1, idx = 0;
while (l <= r)
{int mid = l + r >> 1;if (a[mid] <= x){idx = mid;l = mid + 1; // 继续往右区间找}else if (a[mid] > x) r = mid - 1;
}
下面讲第二种: while (l < r) 在l == r时退出
大家可以发现这种写法不需要 idx 这个变量来记录最终查找的x的起始下标或结束下标了, 因为最后l就是对应的起始下标或结束下标。(r等于l, 所以用r也行)
查找起始下标
int l = 0, r = n - 1;
while (l < r)
{int mid = l + r >> 1; // 区间分成了两个 [l, mid] 和 (mid, r]if (a[mid] < x) l = mid + 1;// 当a[mid] == x的时候, r一直往左, 所以当有多个相同的x的话, 会查找到第一个else if (a[mid] >= x) r = mid; // 因为a[mid]可能 == x, 因为mid也可能满足条件, 所以区间变成[l, mid]
}查找结束下标
int l = 0, r = n - 1, idx = 0;
while (l < r)
{ int mid = l + r + 1 >> 1; // 区间分成了两个 [l, mid) 和 [mid, r]if (a[mid] > x) r = mid - 1;// 当a[mid] == x的时候, l一直往右, 所以当有多个相同的x的话, 会查找到最后一个else if (a[mid] <= x) l = mid; // 因为a[mid]可能 == x, 因为mid也可能满足条件, 所以区间变成[mid, r]
}
接下来讲一下第二种查找结束下标的时候 为什么是 mid = l + r + 1 >> 1,而不是 mid = l + r >> 1;
c++默认向0取整, 对于正整数你可以说是向下取整, 也就是 5 / 2 = 2,
当出现 l = r - 1 的时候, 此时 mid = (l + r) / 2 向下取整后等于 r - 1 , 如果此时进入了a[mid] <= x的分支, 那么 l = mid = r - 1, 这时会发现 l 没有发生变化, 那么就会一直陷入死循环
先更到这里, 后面再补充
觉得写的不错的话, 点个赞吧
相关文章:
原创)
二分查找算法详讲(三种版本写法)原创
介绍: 二分查找算法(Binary Search)是一种在有序数组中查找目标元素的算法。 它的基本思想是通过将目标元素与数组的中间元素进行比较,从而将搜索范围缩小一半。 如果目标元素等于中间元素,则搜索结束;如果目标元素小…...
之commit之前自动执行脚本)
Git钩子(Hooks)之commit之前自动执行脚本
介绍 官方文档: 英文:https://git-scm.com/book/en/v2/Customizing-Git-Git-Hooks中文:https://git-scm.com/book/zh/v2/自定义-Git-Git-钩子 下面只复制了pre-commit部分文档,其他详见官方文档。 Git Hooks Like many other…...

nano机器人2:机械臂的视觉抓取
前言 参考链接: 【机械臂入门教程】机械臂视觉抓取从理论到实战 GRCNN 通过神经网络,先进行模型训练,在进行模型评估。 机械臂逆运动学求解 所有串联型6自由度机械臂均是可解的,但这种解通常只能通过数值解法得到,计算难度大&am…...

技术速递|宣布 Java on Azure 开发工具支持 Java on Azure Container Apps
作者:Jialuo Gan 排版:Alan Wang 在 Microsoft Build 2024 期间宣布,Azure Container Apps 现在可为 Java 开发人员提供丰富的操作功能。(详细内容请参见本博客)。 我们很高兴地与大家分享,Azure Toolkit for Intelli…...
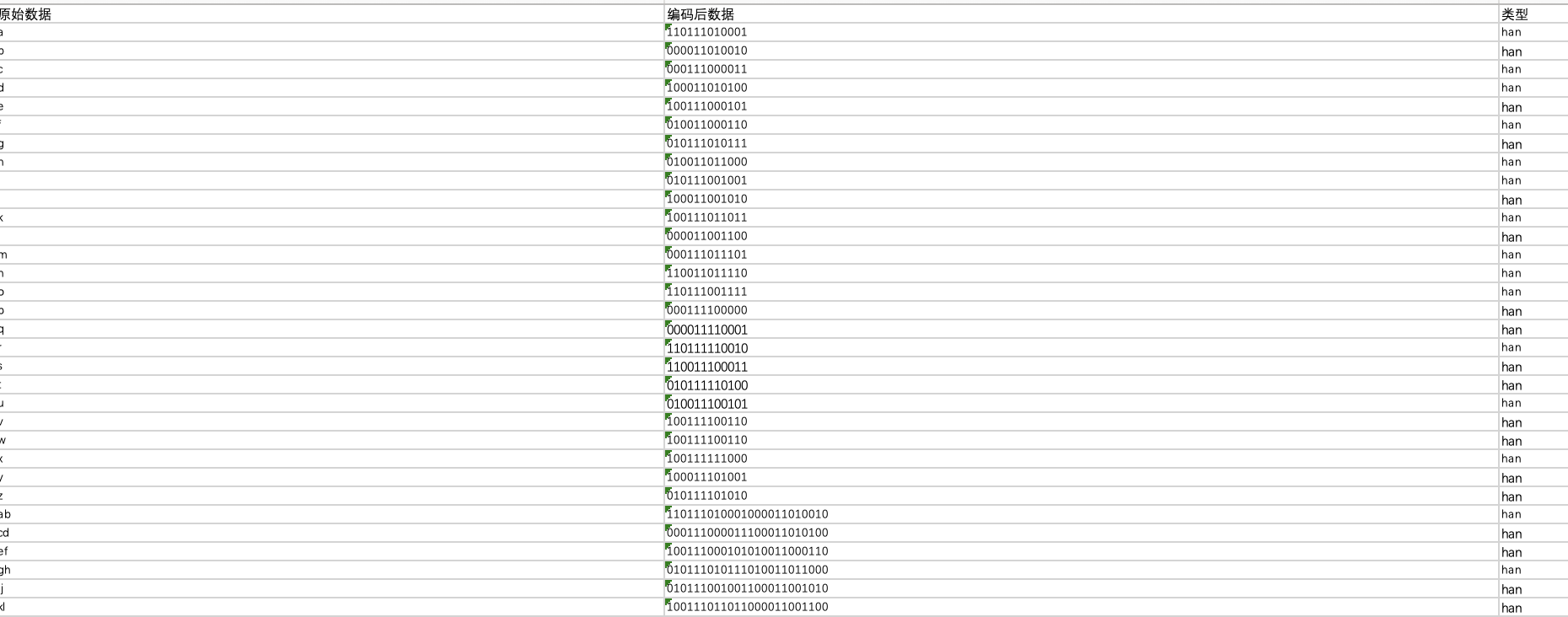
随机森林算法实现分类
随机森林算法实现对编码后二进制数据的识别 1.直接先上代码! import numpy as np import pandas as pd from sklearn.model_selection import train_test_split, GridSearchCV from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import …...

Ubuntu卸载软件
在删除这些目录之前,你必须确定一个非常重要的事情:确认没有任何服务正在使用这些版本的 PHP。如果你删除了正在使用的 PHP 版本的扩展目录,那么依赖于这个版本的 PHP 的网站或服务可能会停止工作。 如果你确定某个版本的 PHP 没有在使用中&…...

网络工程师:网络可靠性技术
一、可靠性 平均故障间隔时间MTBF(Mean Time Between Failure)和平均修复时间MTTR(Mean Time to Repair)这两个指标来评价系统的可靠性。 1、平均故障间隔时间MTBF MTBF是指一个系统无故障运行平均时间,通常以小时为单位。MTBF越大可靠性越高。 2、平均修复时间MTTR…...

科技引领未来:高速公路可视化
高速公路可视化监控系统利用实时视频、传感器数据和大数据分析,通过图扑 HT 可视化展示交通流量、车速、事故和路况信息。交通管理人员可以实时监控、快速响应突发事件,并优化交通信号和指挥方案。这一系统不仅提高了道路安全性和车辆通行效率࿰…...

Golang发送POST请求并传递JSON数据
客户端 package mainimport ("c02_get_param/common""fmt""zdpgo_resty" )func main() {// Create a Resty Clientclient : zdpgo_resty.New()// 设置字符串resp, err : client.R().SetHeader("Content-Type", "application/jso…...

C++实现生产者消费者模型
生产者-消费者模型是一种典型的多线程并发模式,常用于在一个共享缓冲区中协调生产者和消费者之间的数据传递。在C中,我们可以使用标准库中的线程、互斥量和条件变量来实现该模型。以下是一个简单的生产者-消费者模型的实现示例: #include &l…...

【Mac】MWeb Pro(好用的markdown编辑器) v4.5.9中文版安装教程
软件介绍 MWeb Pro for Mac是一款Mac上的Markdown编辑器软件,它支持实时预览,语法高亮,自动保存和备份等功能,并且有多种主题和样式可供选择。此外,MWeb还支持多种导出格式,包括HTML、PDF、Word、ePub等&a…...

C++ | Leetcode C++题解之第118题杨辉三角
题目: 题解: class Solution { public:vector<vector<int>> generate(int numRows) {vector<vector<int>> ret(numRows);for (int i 0; i < numRows; i) {ret[i].resize(i 1);ret[i][0] ret[i][i] 1;for (int j 1; j &…...

3D透视图转的时候模型闪动怎么解决?---模大狮模型网
在3D建模与渲染的世界中,透视图是我们观察和操作模型的重要窗口。然而,有时候在旋转透视图时,模型会出现闪动的现象,这不仅影响了我们的工作效率,还可能对最终的渲染效果产生负面影响。本文将探讨这一问题的成因&#…...
如何创建一个vue项目?详细教程,如何创建第一个vue项目?
已经安装node.js在自己找的到的地方新建一个文件夹用于存放项目,记住文件夹的存放路径,以我为例,我的文件夹路径为D:\tydic 打开cmd命令窗口,进入刚刚的新建文件夹 切换硬盘: D: 进入文件夹:cd tydic 使…...

AWS迁移与传输之Migration Hub
AWS Migration Hub是一种集中化的迁移管理服务,可帮助企业规划、跟踪和管理在亚马逊云中进行的各种迁移活动。包括应用程序迁移、数据库迁移、服务器迁移等。 AWS Migration Hub (Migration Hub) 提供一个位置来跟踪使用多个 AWS 工具和合作伙伴解决方案的迁移任务…...

网络渗透思考
1. windows登录的明文密码,存储过程是怎么样的,密文存在哪个文件下,该文件是否可以打开,并且查看到密文 windows的明文密码:是通过LSA(Local Security Authority)进行存储加密的 存储过程:当用户输入密码之…...

2.8万字总结:金融核心系统数据库升级路径与场景实践
OceanBase CEO 杨冰 谈及数字化转型,如果说过去还只是头部金融机构带动效应下的“选择题”。那么现在,我相信数字化转型已经成为不论大、中、小型金融机构的“必答题”。 本文为OceanBase最新发布的《万字总结:金融核心系统数据库升级路径…...
Linux:进程控制(二.详细讲解进程程序替换)
上次讲了:Linux:进程地址空间、进程控制(一.进程创建、进程终止、进程等待) 文章目录 1.进程程序替换1.1概念1.2原理1.3使用一个exec 系列函数execl()函数结论与细节 2.多进程时的程序替换3.其他几个exec系…...
Elasticsearch8.13.4版本的Docker启动关闭HTTPS
博主环境是: 开发环境:SpringbootElasticSearch客户端对应的starter 2.6.3版本 maven配置 <!-- ElasticSearch --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elas…...
- ION简化版本)
linux 之dma_buf (8)- ION简化版本
一、前言 我们学习了如何使用 alloc_page() 方式来分配内存,但是该驱动只能分配1个PAGE_SIZE。本篇我们将在上一篇的基础上,实现一个简化版的ION驱动,以此来实现任意 size 大小的内存分配。 二、准备 为了和 kernel 标准 ion 驱动兼容&…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
