数据结构——图
一 图论基本概念

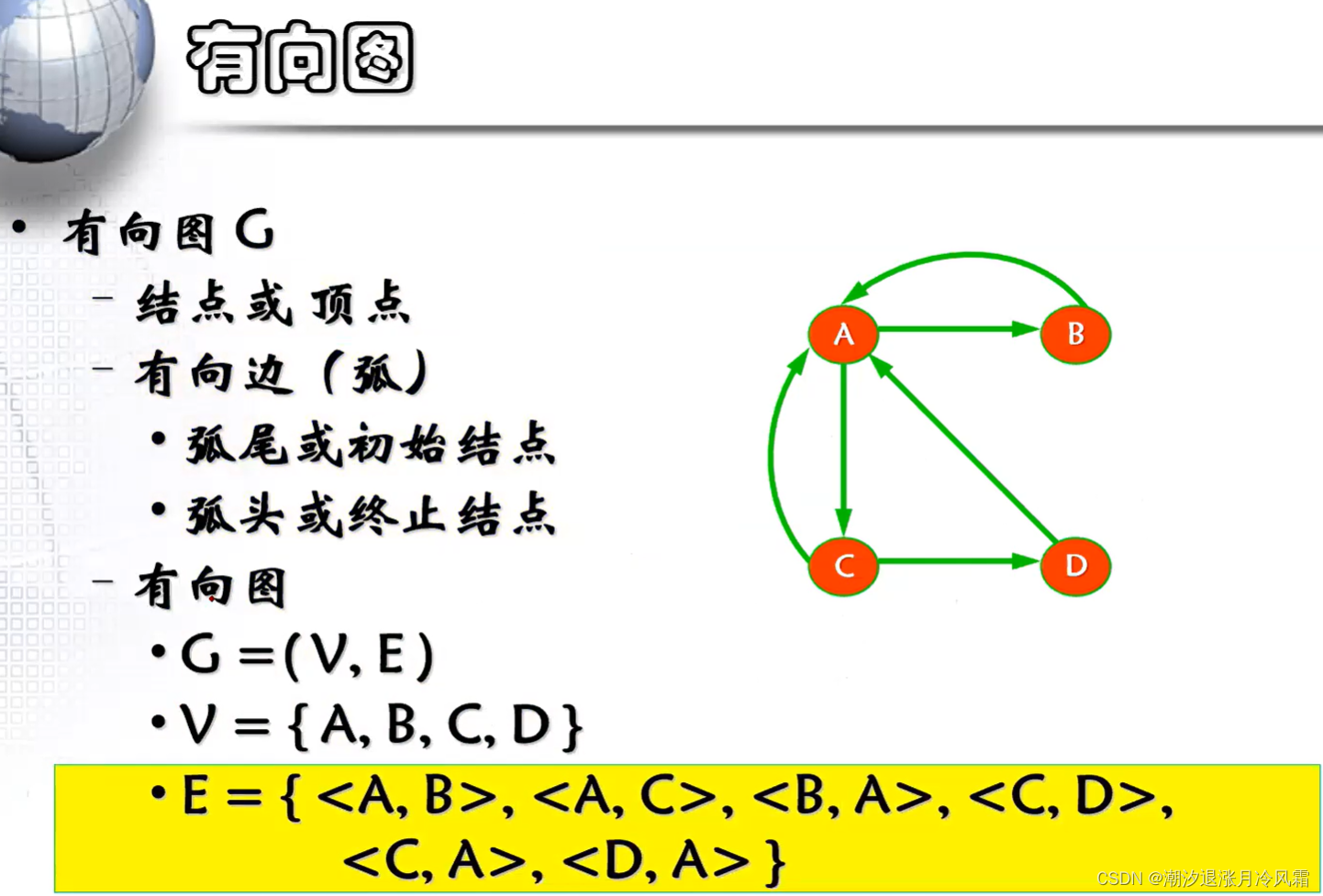
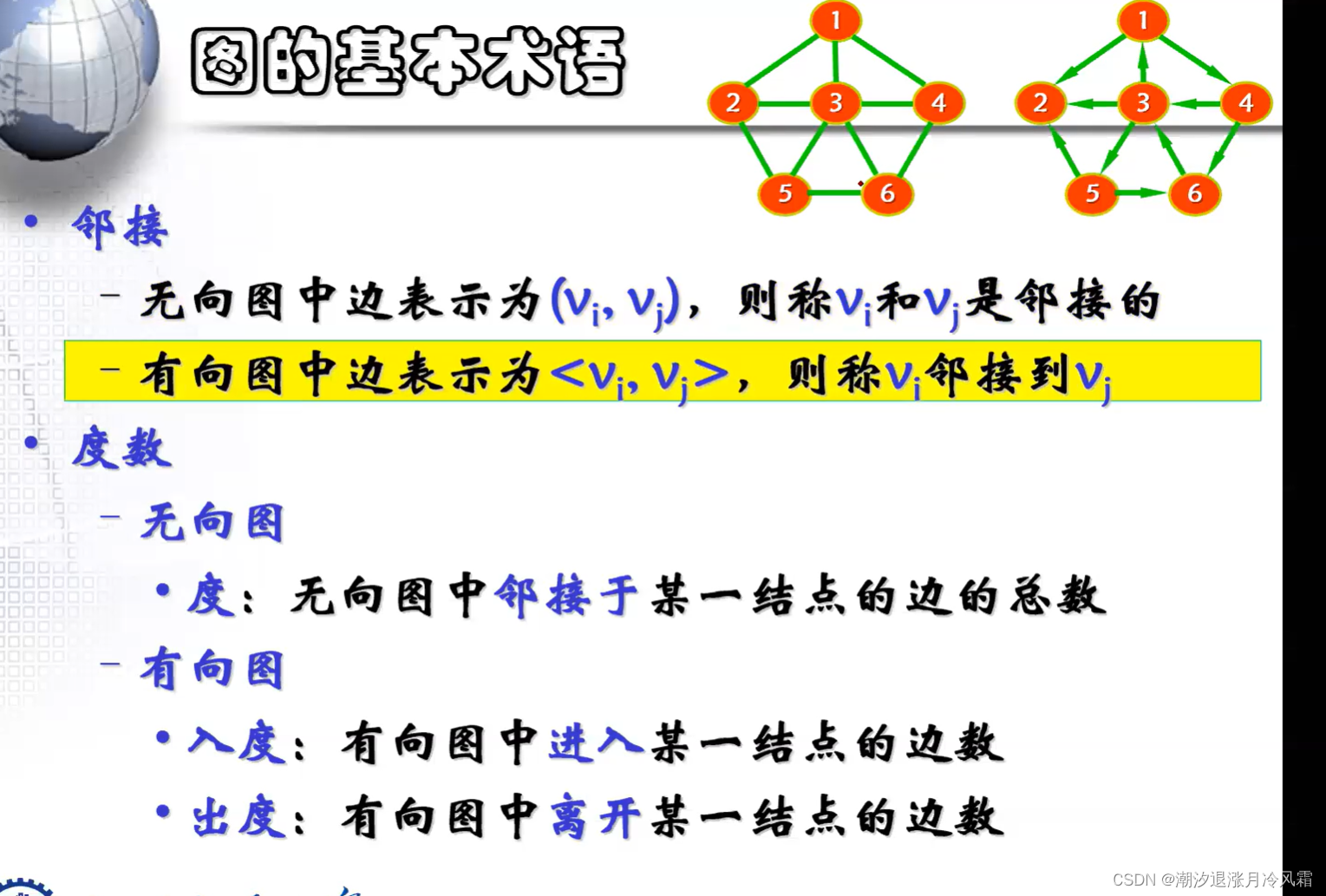


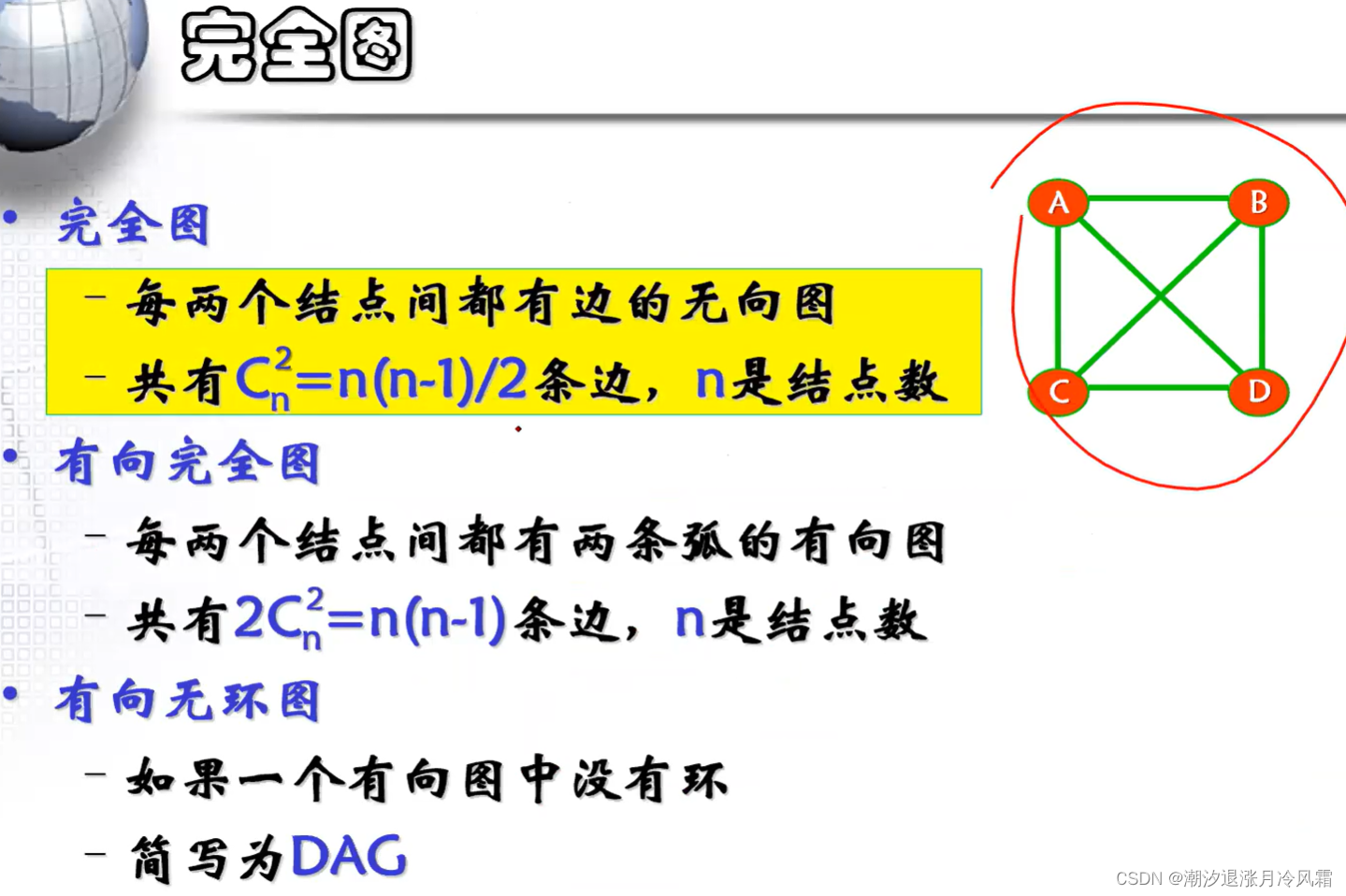
Directed Acyclic Graph (DAG)
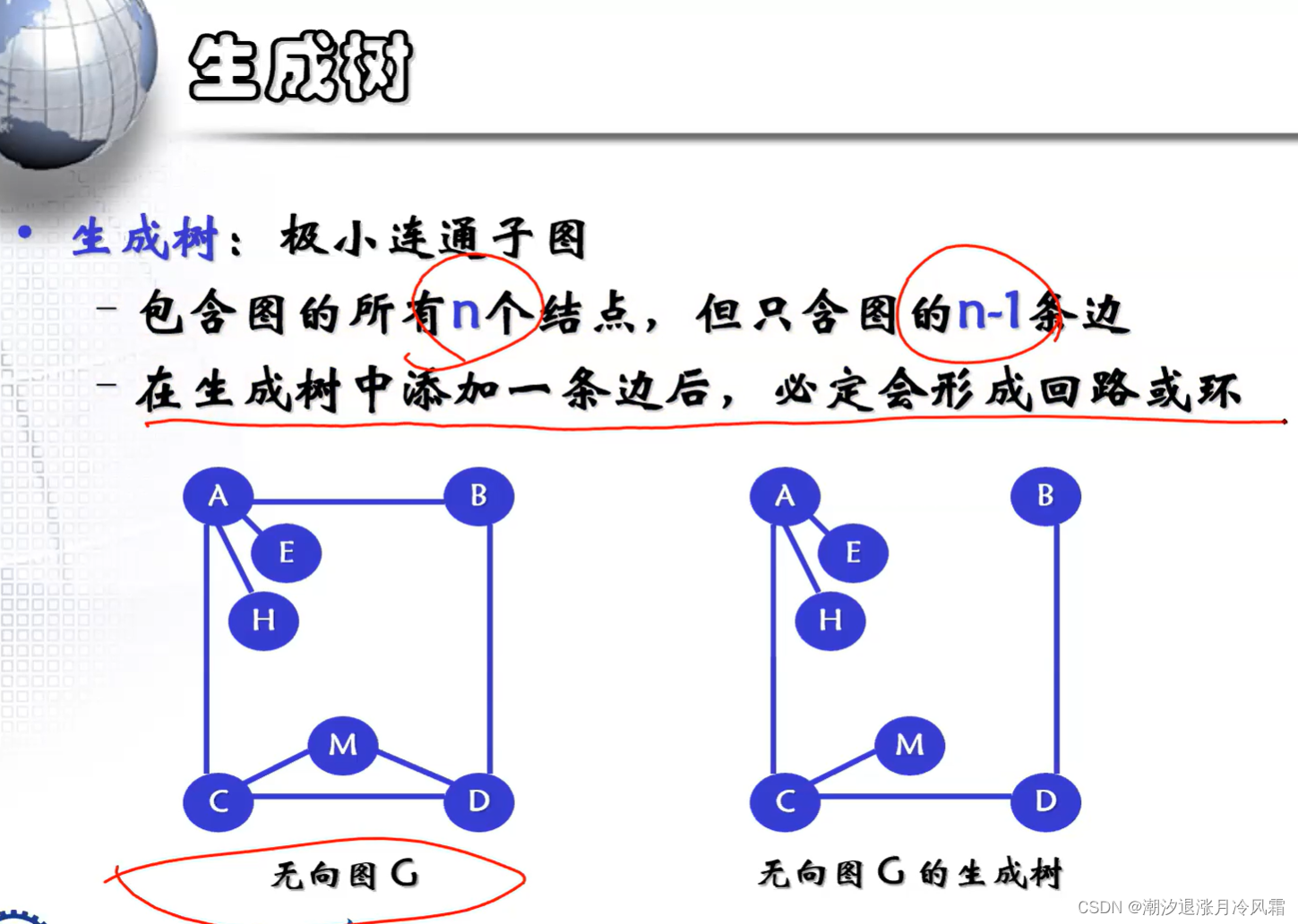
二 图的存储
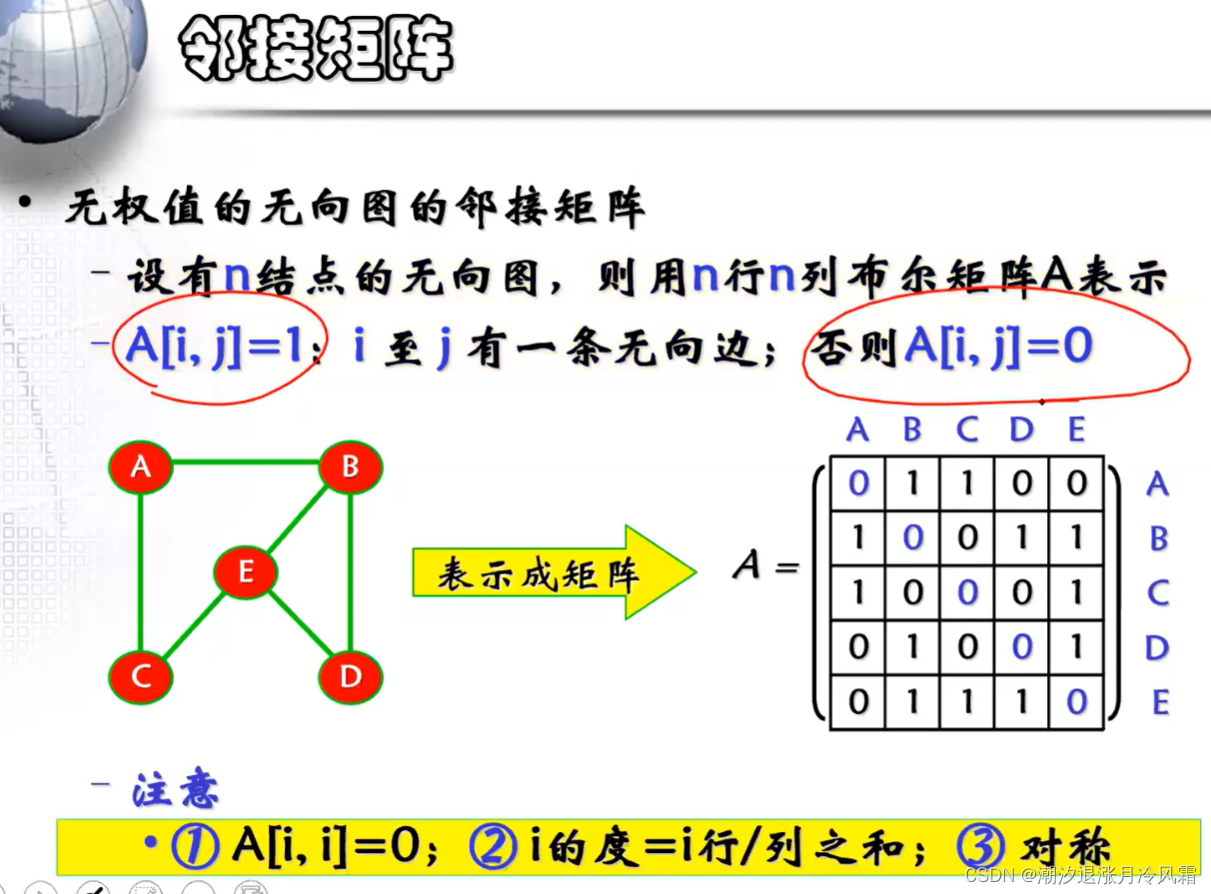
①邻接矩阵(适用于稠密图)
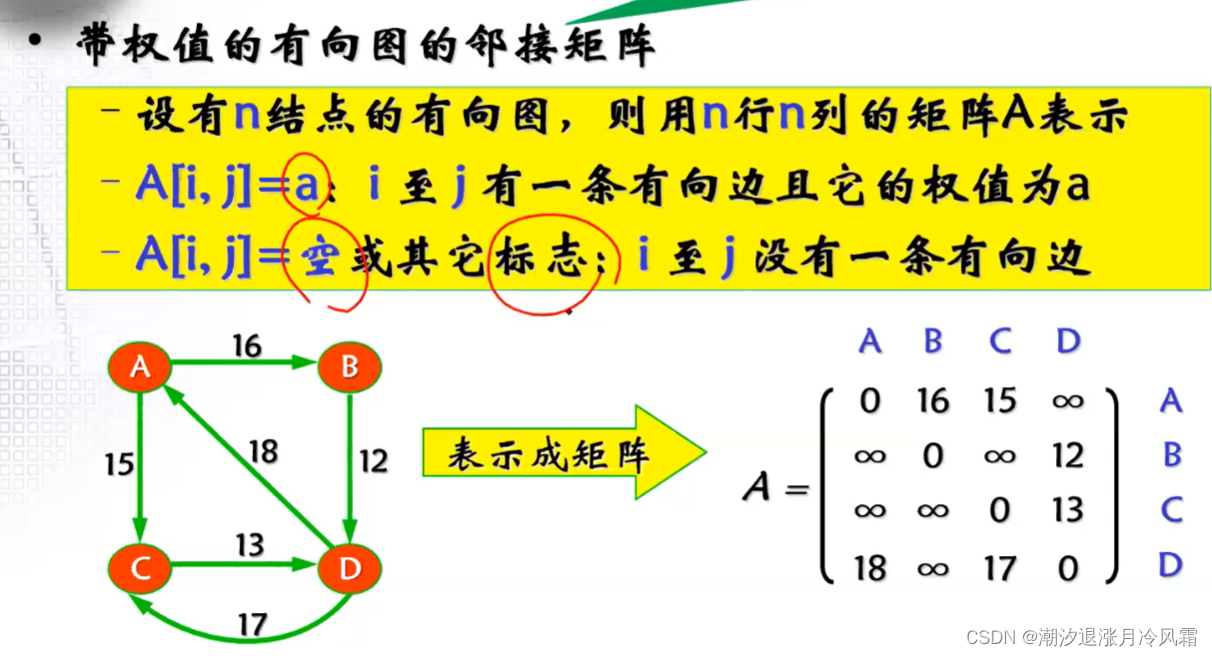
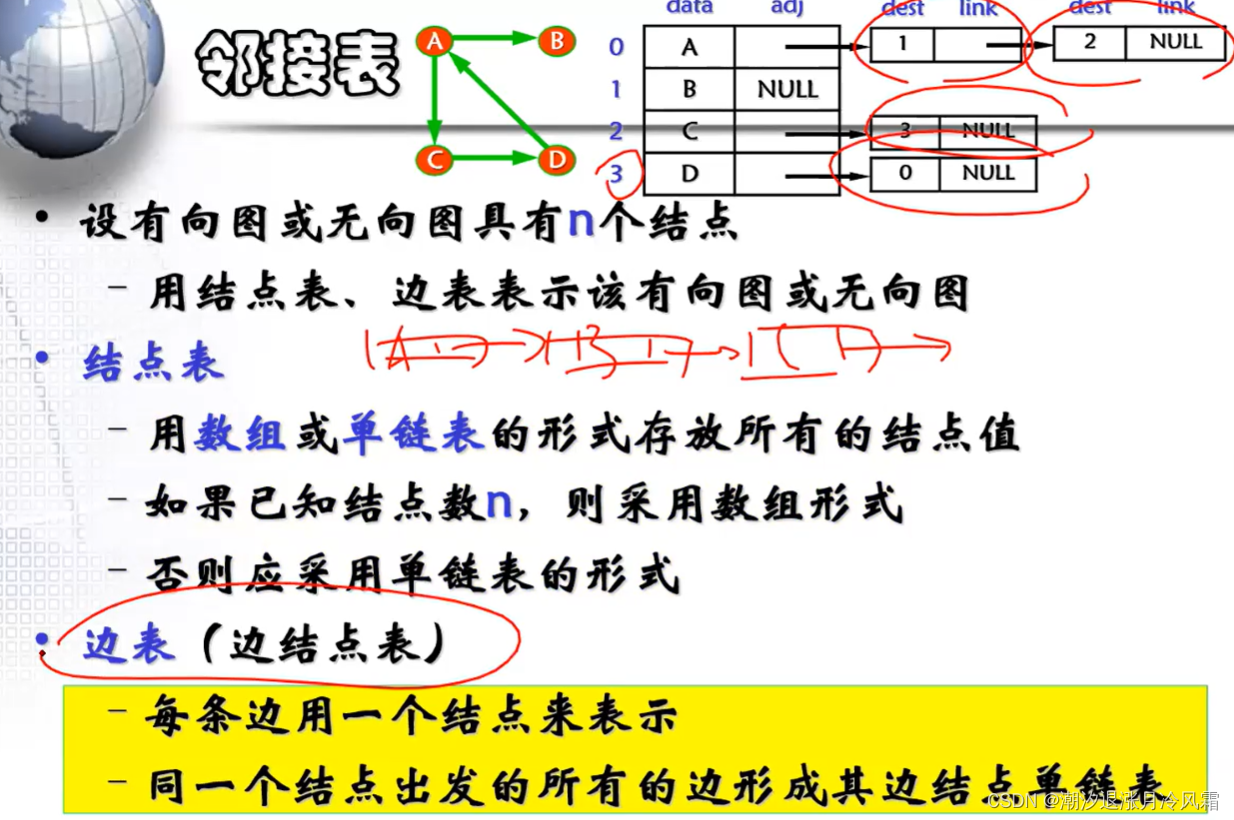
②邻接表(适用于稀疏图)
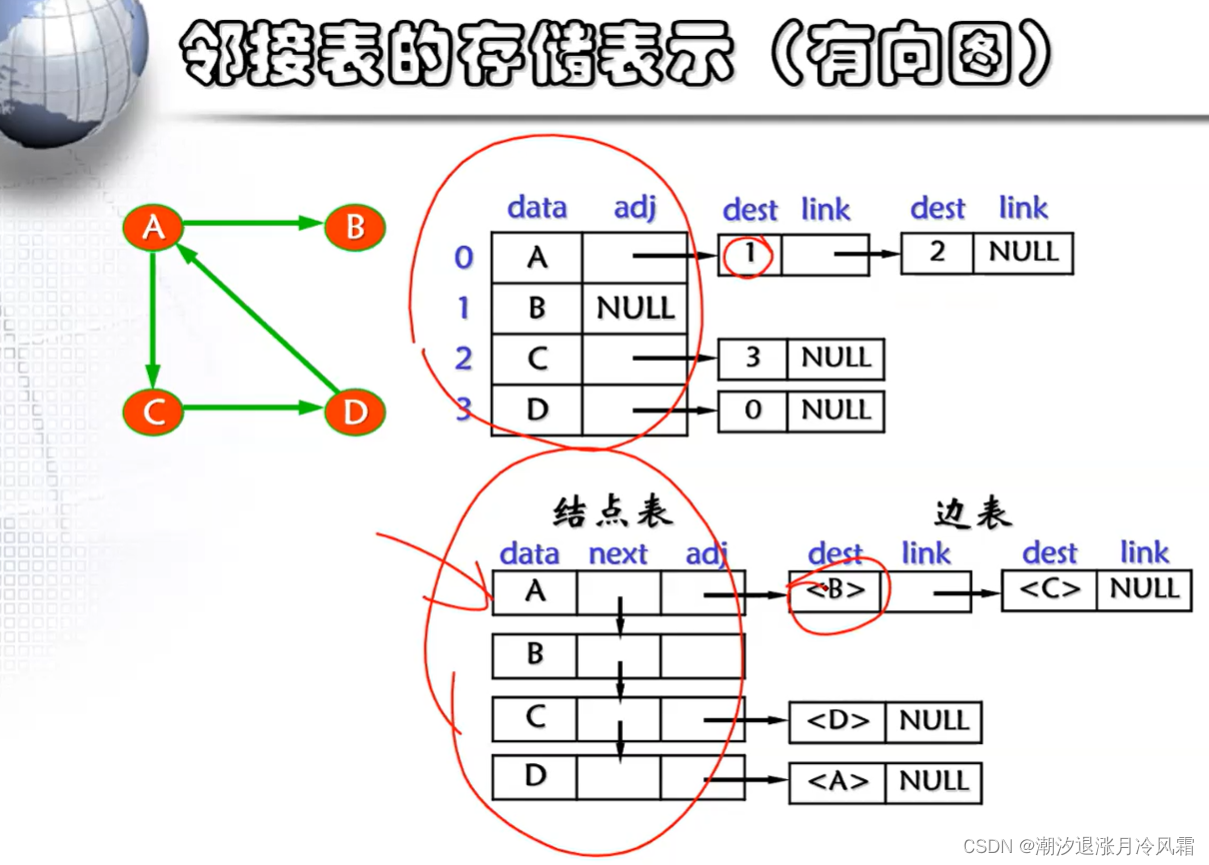

三、图的遍历
①深度优先搜索
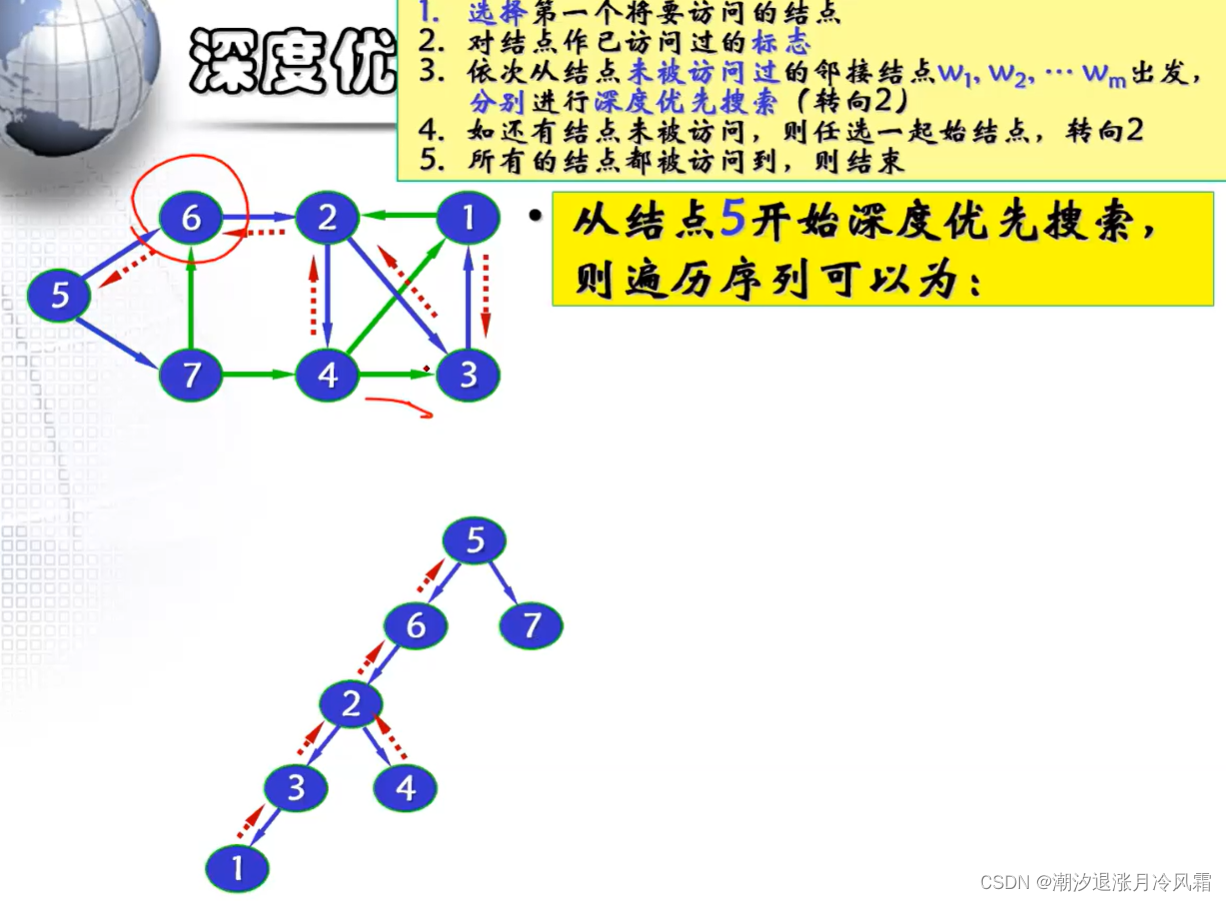
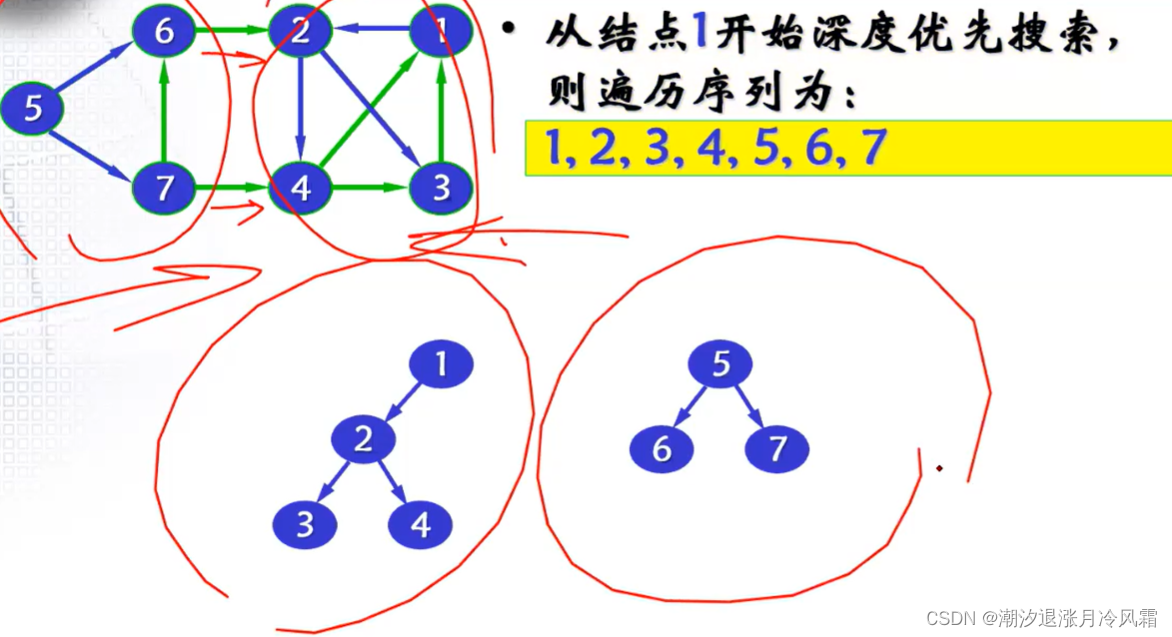
//(基于邻接表实现,以有向图为例)
//DFS:Depth First Search 深度优先搜索
//1、访问起始顶点 2、访问一个未访问过的邻接顶点 3、若所有邻接顶点都已被访问,则回溯 4、所有顶点都被访问,遍历结束
void dfs(int start, bool visited[])
{//访问起始结点cout << verList[start].ver << '\t';visited[start] = true;//找到顶点表中该顶点对应的链表edgeNode* node = verList[start].head;while (node){if (!visited[node]) dfs(visited[node],visited); //访问未访问过的邻接结点node = node->next; //跳过已访问的结点}//当所有邻接结点都已被访问,则回溯
} //递归函数结束时,生成一棵深度优先搜索树void dfs()
{//访问标志数组初始化bool* visited=new bool[Vers]; //Vers:顶点数量for (int i = 0; i < Vers; i++)Vers[i] = false;for (int i = 0; i < Vers; i++){if (visited[i] == true) continue; //寻找下一个树遍历的起始结点dfs(i, visited);} //生成深度优先搜索森林(起点选择不同,生成结果不同,有些情况能只生成一棵树)
}DFS将所有边和顶点遍历一次,若采用邻接数组,时间复杂度为O(V²),若采用邻接矩阵,时间复杂度为O(V+E)。
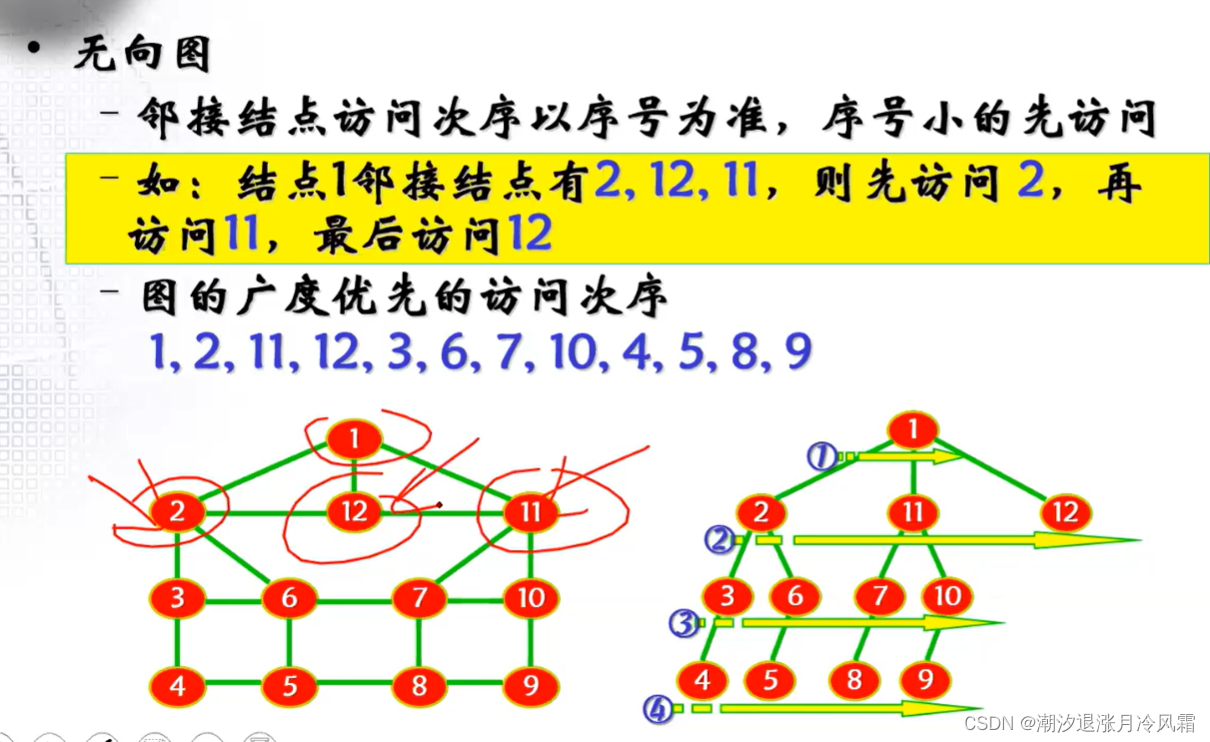
②广度优先搜索
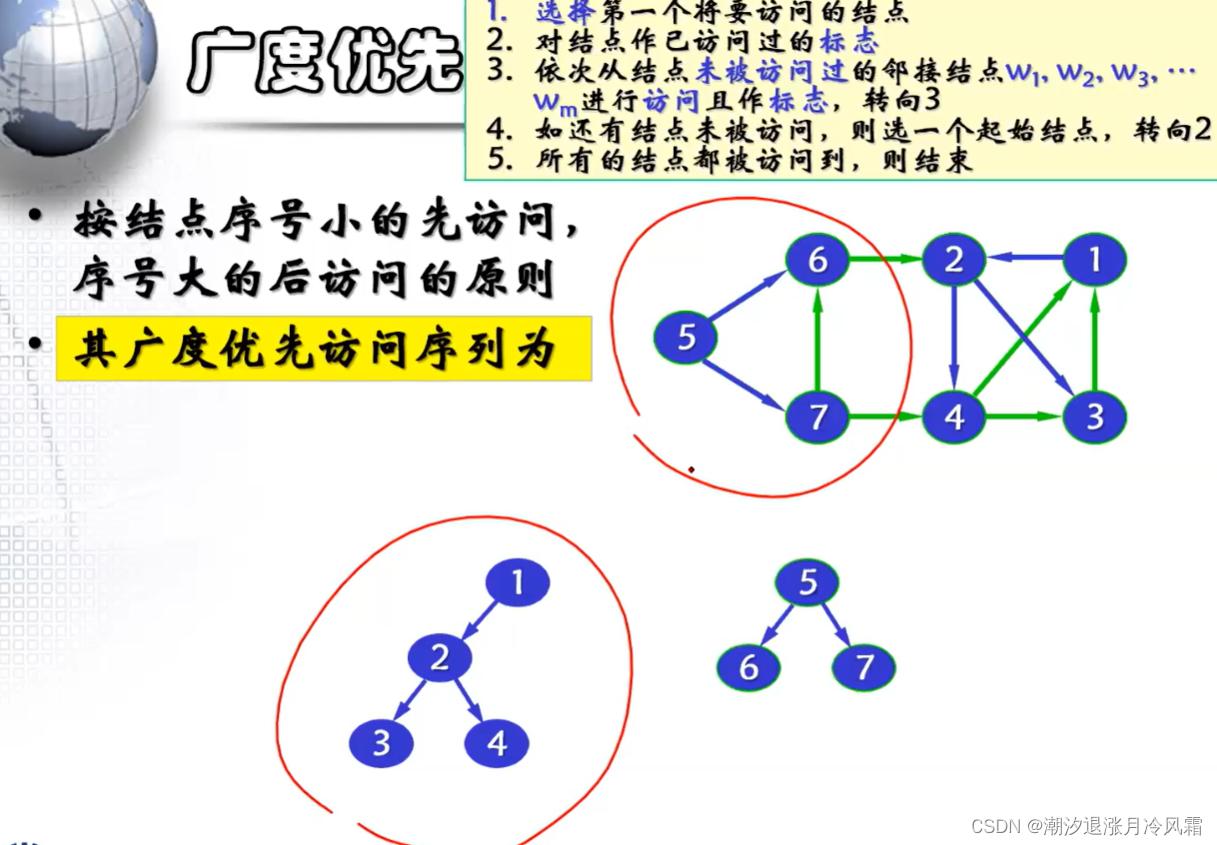

//BFS:Breadth First Search 广度优先搜索
//1、访问起始顶点 2、依次访问起始顶点的所有未访问的邻接结点 3、所有顶点都被访问,遍历结束
void bfs()
{queue<int> q;bool* visited = new bool[Vers];for (int i = 0; i < Vers; i++)visited[i] = false;for (int i = 0; i < Vers; i++){if (visited[Vers] == true) continue; ///寻找一棵新的搜索树的起始结点q.push(i); //结点入队,开始一棵搜索树的生成while (!q.empty()){int currentNode = q.front();q.pop();if (visited[currentNode]) continue; //这里需要注意,比如1的邻接结点2、3入队,而3邻接于2,在访问3的过程中已访问了2,所以2出队时无需再次访问cout << verList[currentNode].ver << '\t'; //访问当前结点visited[currentNode] = true;//找到顶点表中该顶点对应的链表edgeNode* node = verList[currentNode].head;//将未访问的邻接顶点入队while (node){if (!visited[node->end]) q.push(node->end); //将未访问的邻接顶点入队node = node->next;} }}
}
可用优先级队列实现。
BFS将所有边和顶点遍历一次,若采用邻接数组,时间复杂度为O(V²),若采用邻接矩阵,时间复杂度为O(V+E)。
四、图的应用
1、欧拉路径(一笔画问题)
欧拉路径:在图中找到一条路径经过每一条边,且每条边只经过一次
欧拉回路:起点和终点相同的欧拉路径
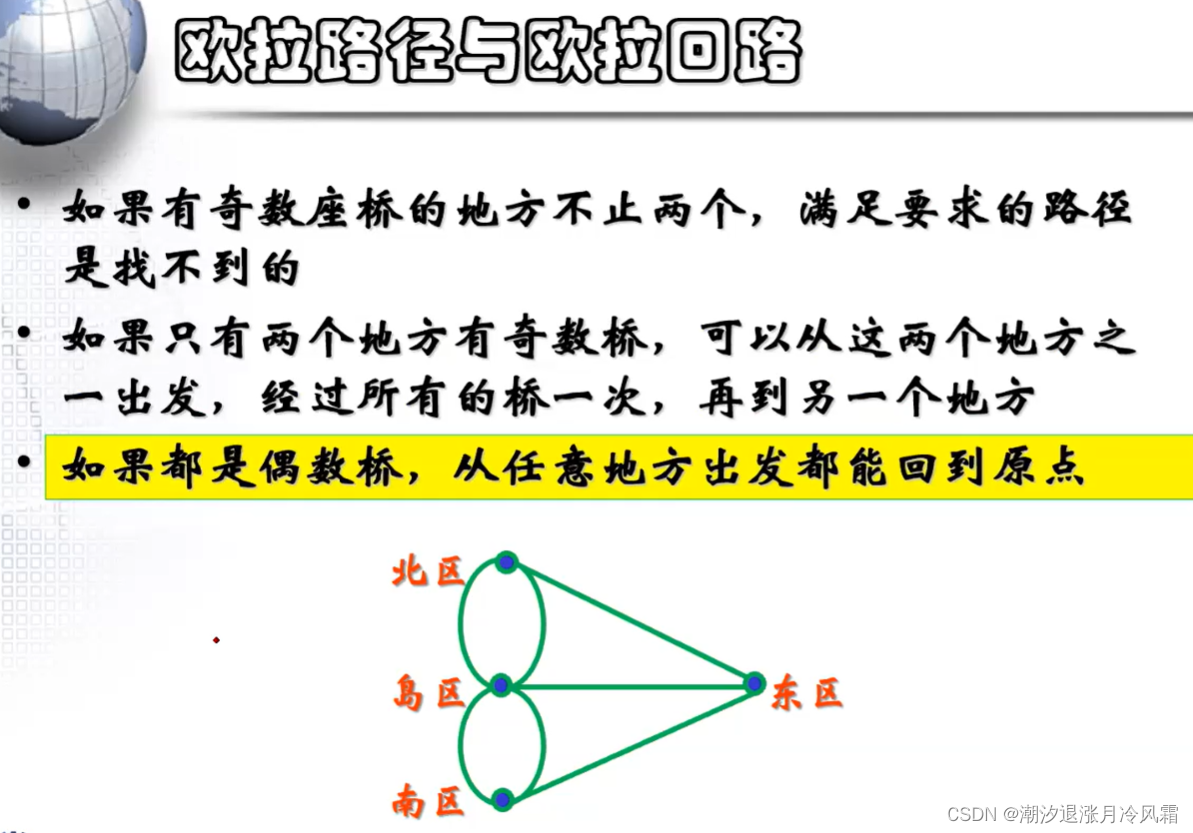
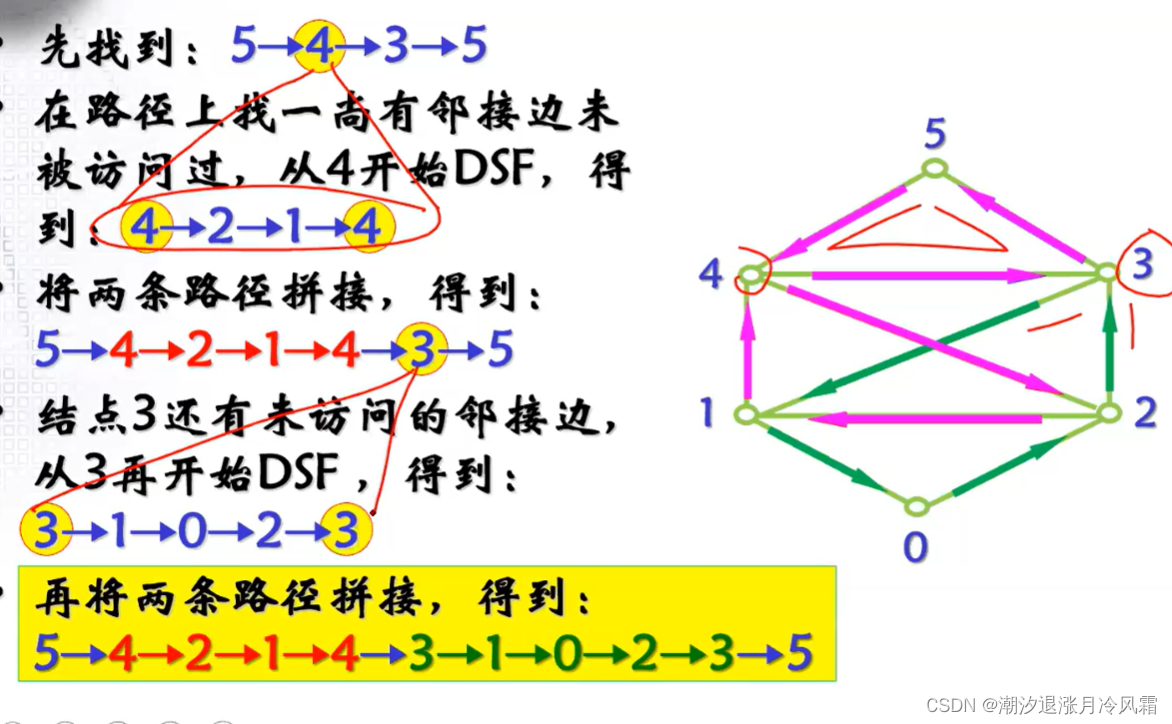
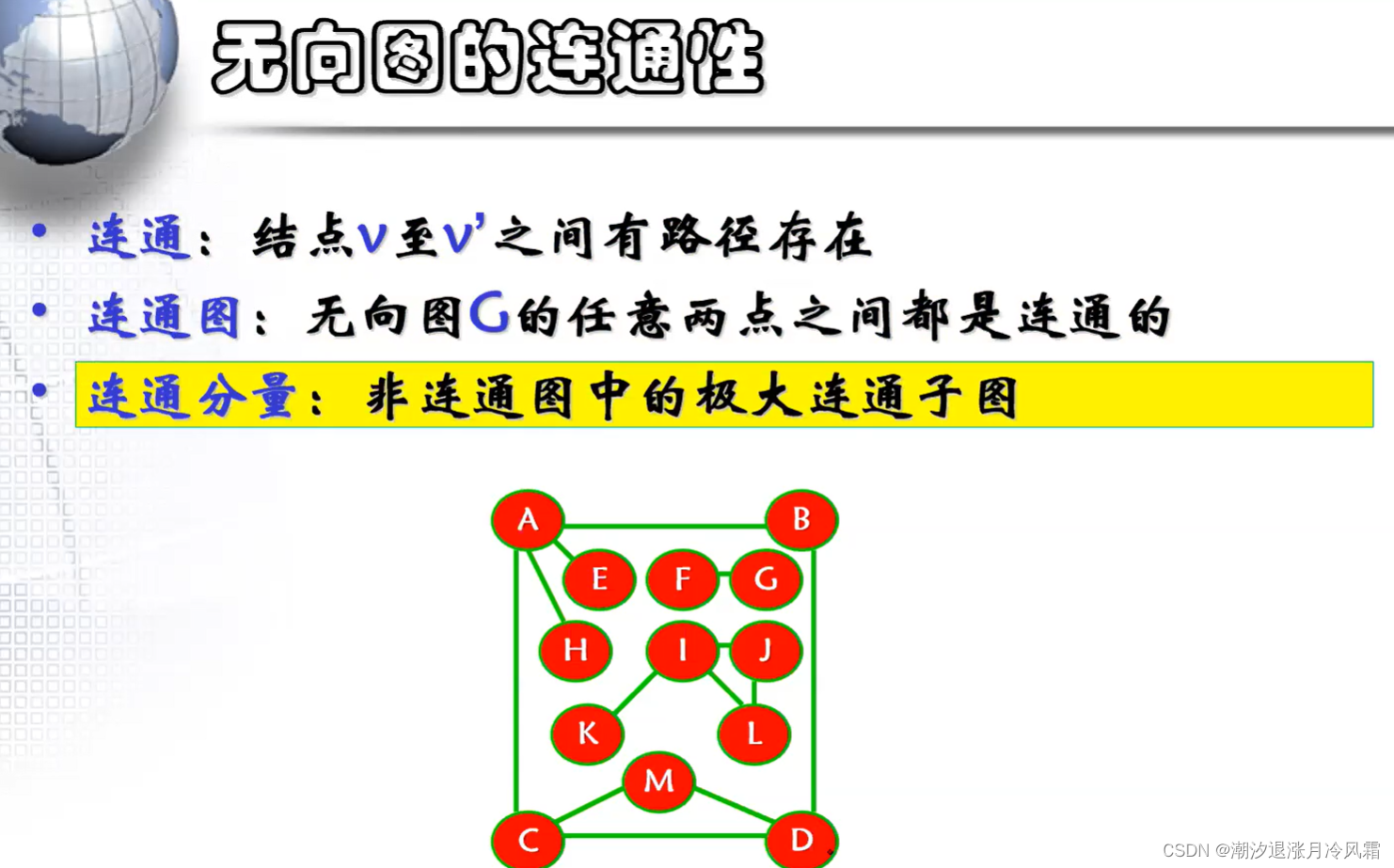
2、图的连通性
①无向图的连通性

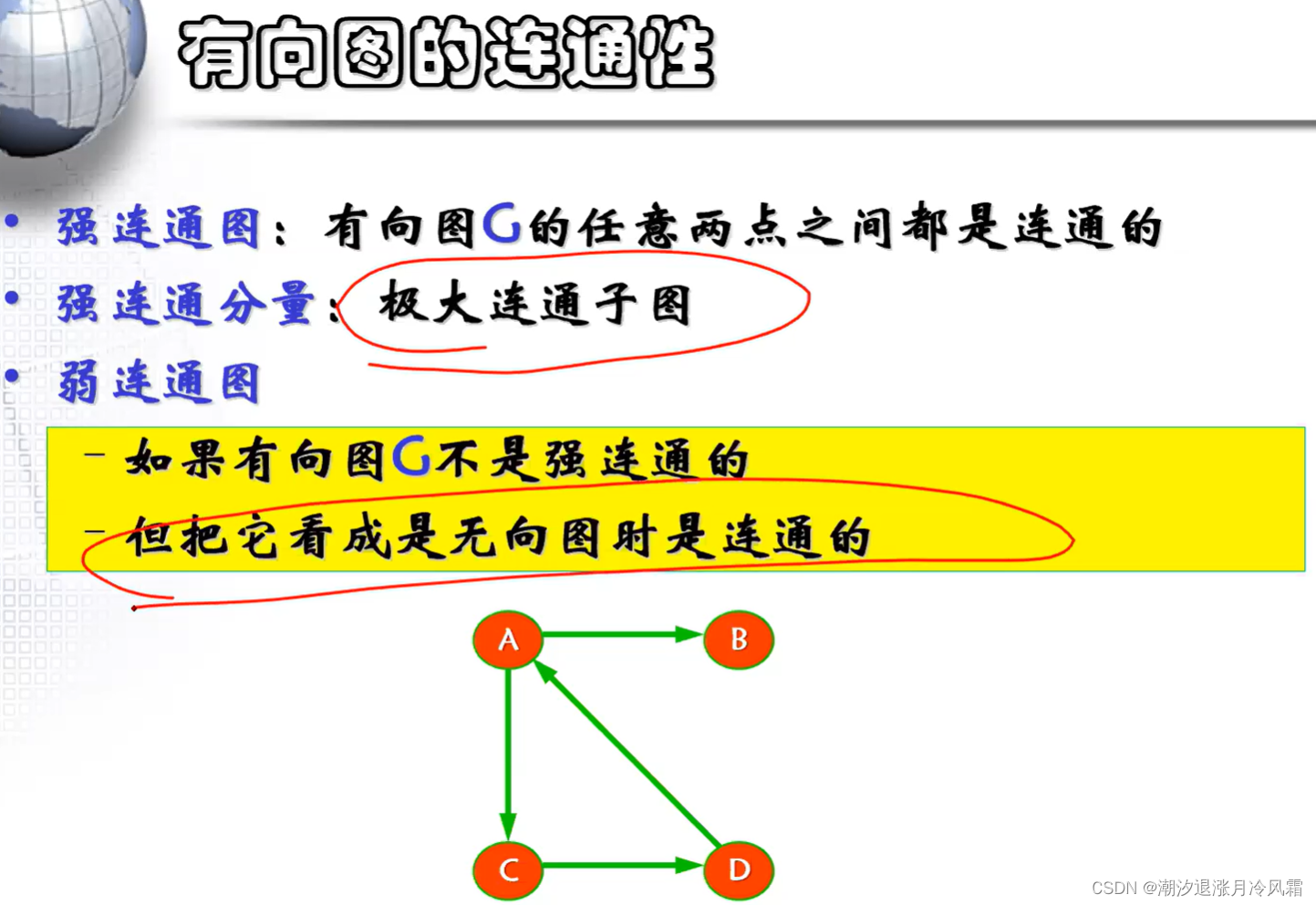
②有向图的连通性(Kosaraju算法)

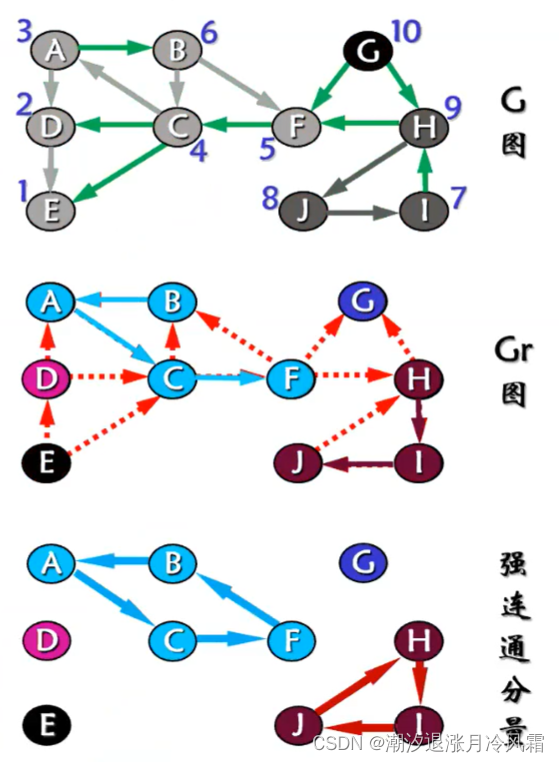
G图和Gr图分别进行一次dfs,时间复杂度为O(V+E)
3、拓扑排序
能进行拓扑排序的图是有向无环图(DAG),顶点表示活动的图称为AOV网((activity on the vertex)
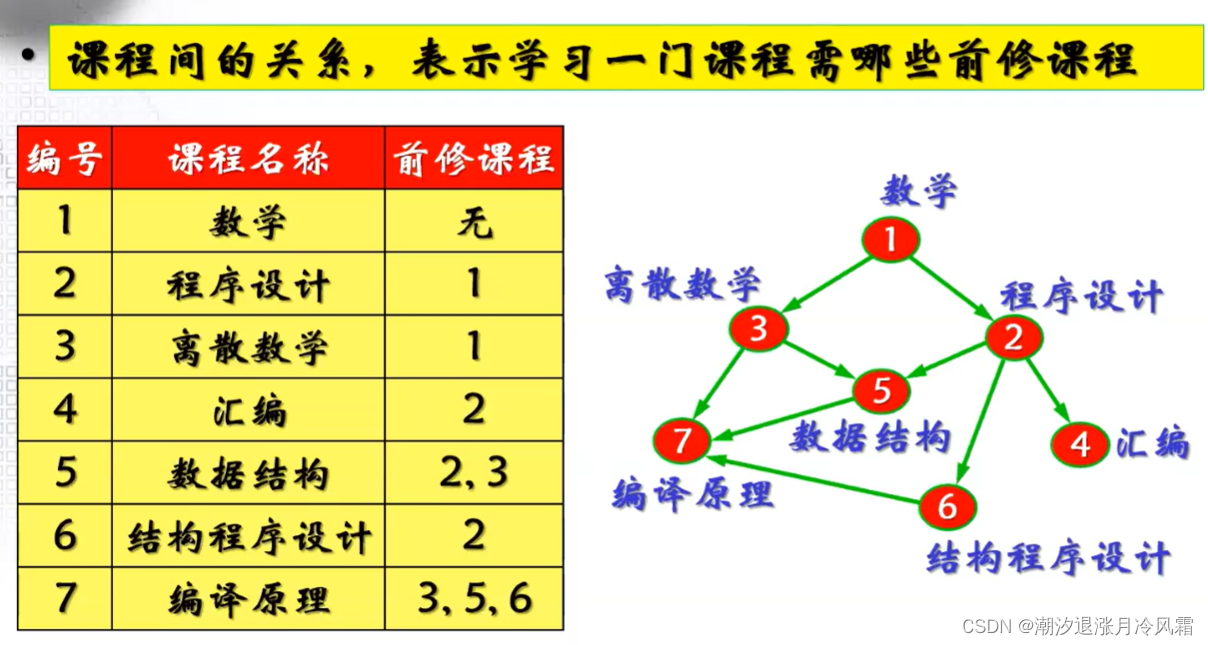
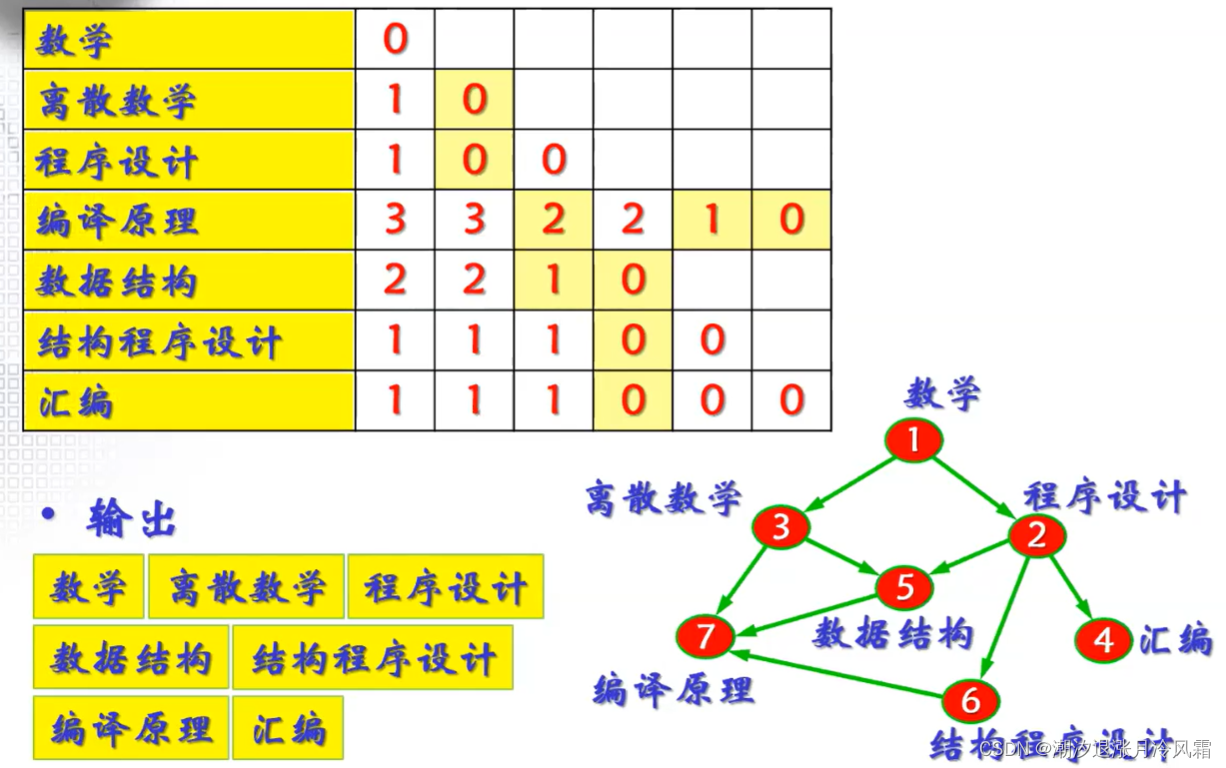


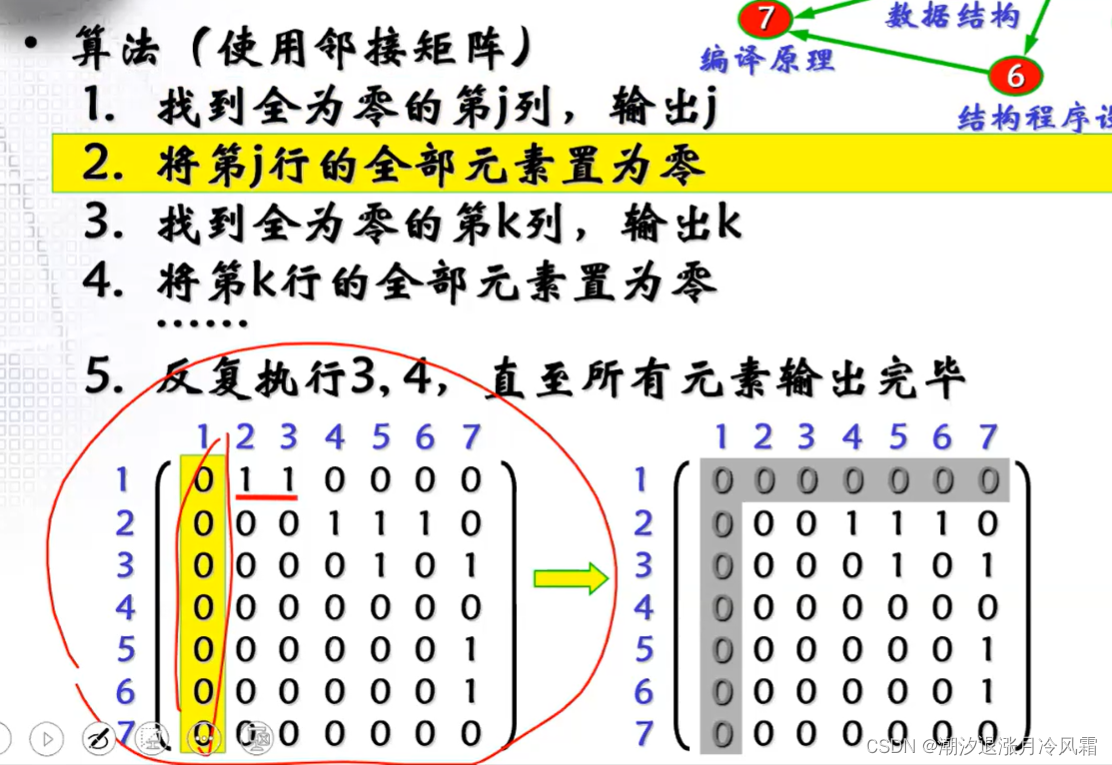
4、关键路径
AOE(activity on the edge)网是另一种有向无环图,有向边的权值表示活动的持续时间,弧尾表示活动的起点,弧头表示活动的终点,边的方向表示事件发生的先后顺序。可以用AOE网表示一项工程,如下图A为工程的源点,G为工程的收点。关键路径具有从源点到收点的最长路径长度,其上的活动称为关键活动。
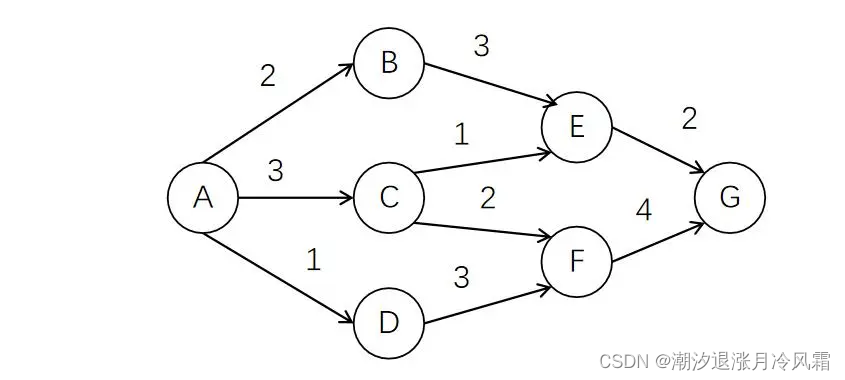
顶点x的最早发生时间为ee(x),最晚发生时间为le(x),定义le(x)-ee(x)=△e(x)为时间余量,满足△e(x)=0的顶点x为关键活动,找到所有时间余量为0的顶点即找到了关键路径。
算法实现:
①进行拓扑排序
②按照拓扑序列,正向遍历每一个顶点x,计算最早发生时间ee(x):
所有顶点的ee初始化为0,假设边<u,v>的长度为Luv,对于每一个顶点u,检查其后继顶点v,若ee(u)+Luv>ee(v),更新ee(v)=ee(u)+Luv 。ee(G)即为工程的最短完成时间,即关键路径的长度Len.
③按照拓扑序列,逆向遍历每一个顶点x,计算最晚发生时间le(x):
所有顶点的le初始化为Len,假设边<u,v>的长度为Luv,对于每一个顶点u,检查其后继顶点v,若le(v)-Luv<le(u),更新le(u)=le(v)-Luv 。
④计算△e(x)=le(x)-ee(x),输出△e(x)=0的顶点即为关键活动,构成一条关键路径。
5、最小生成树
最小生成树:边的权值之和最小的生成树
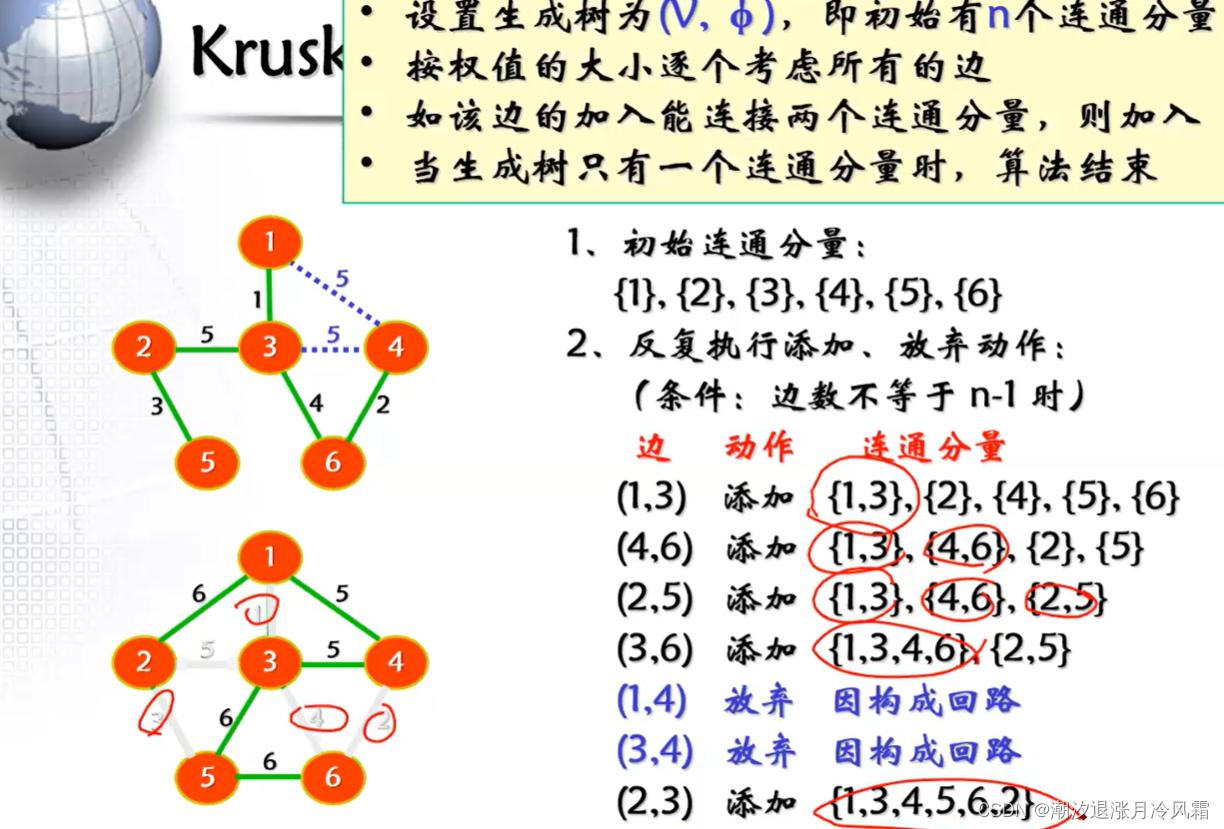
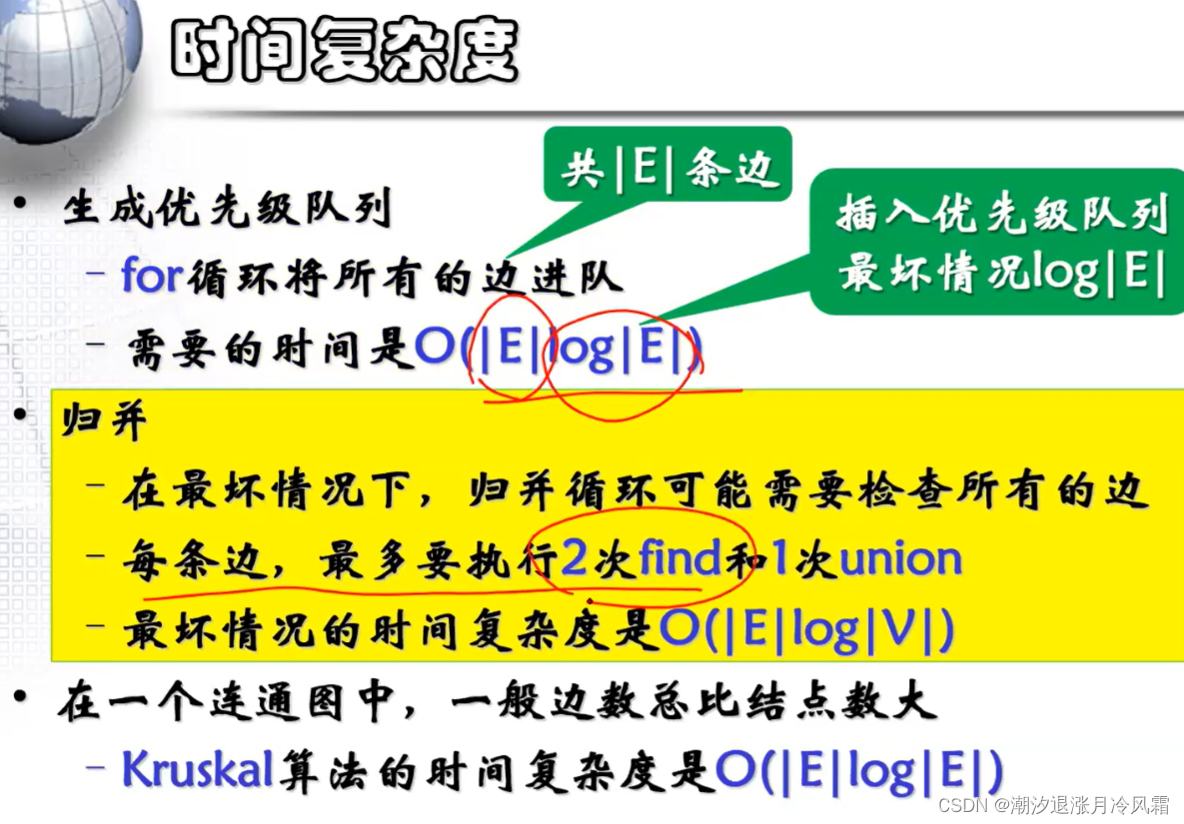
①Kruskal算法
[选择边][优先级队列+并查集]



②Prim算法
[选择点]


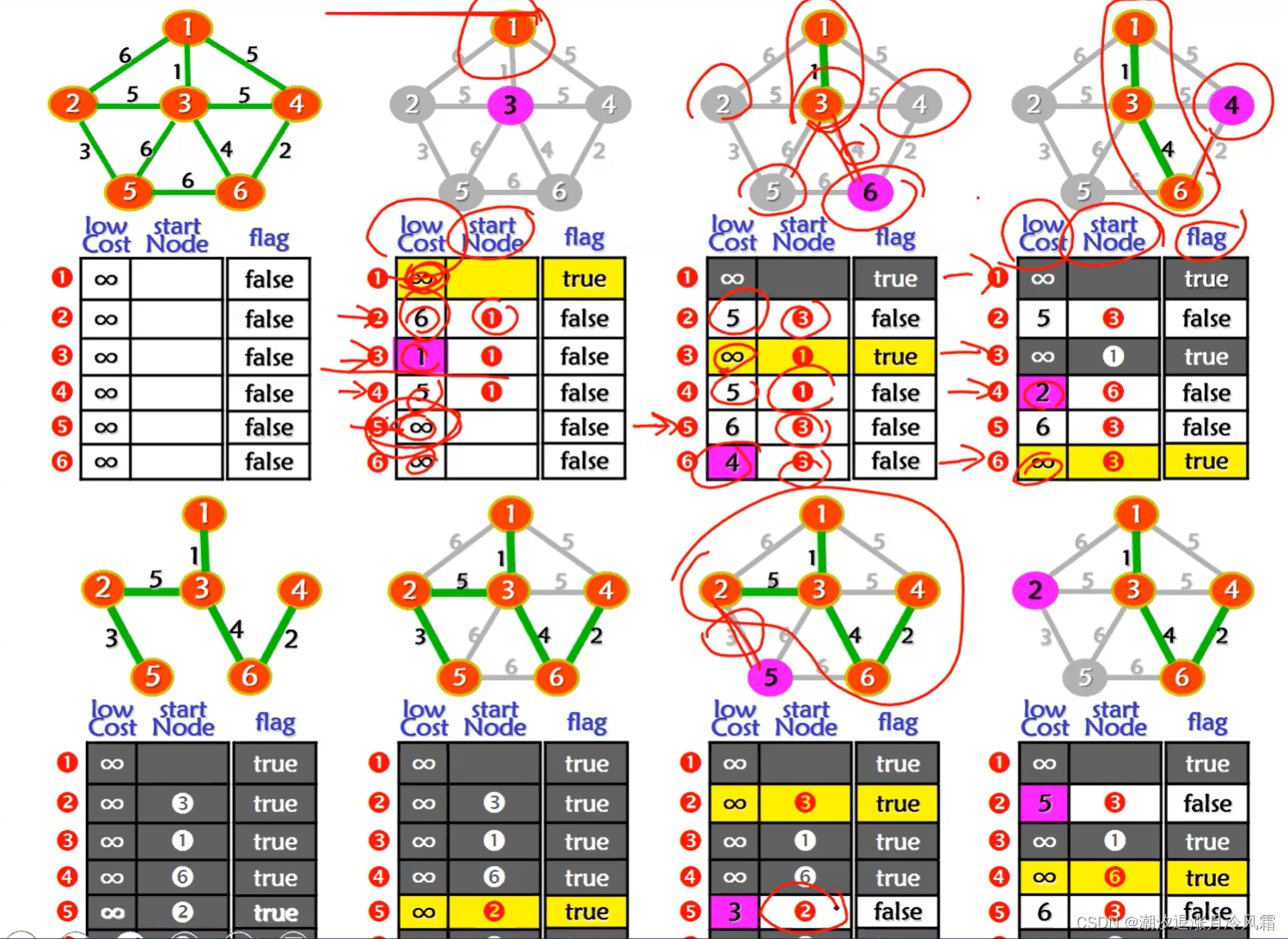


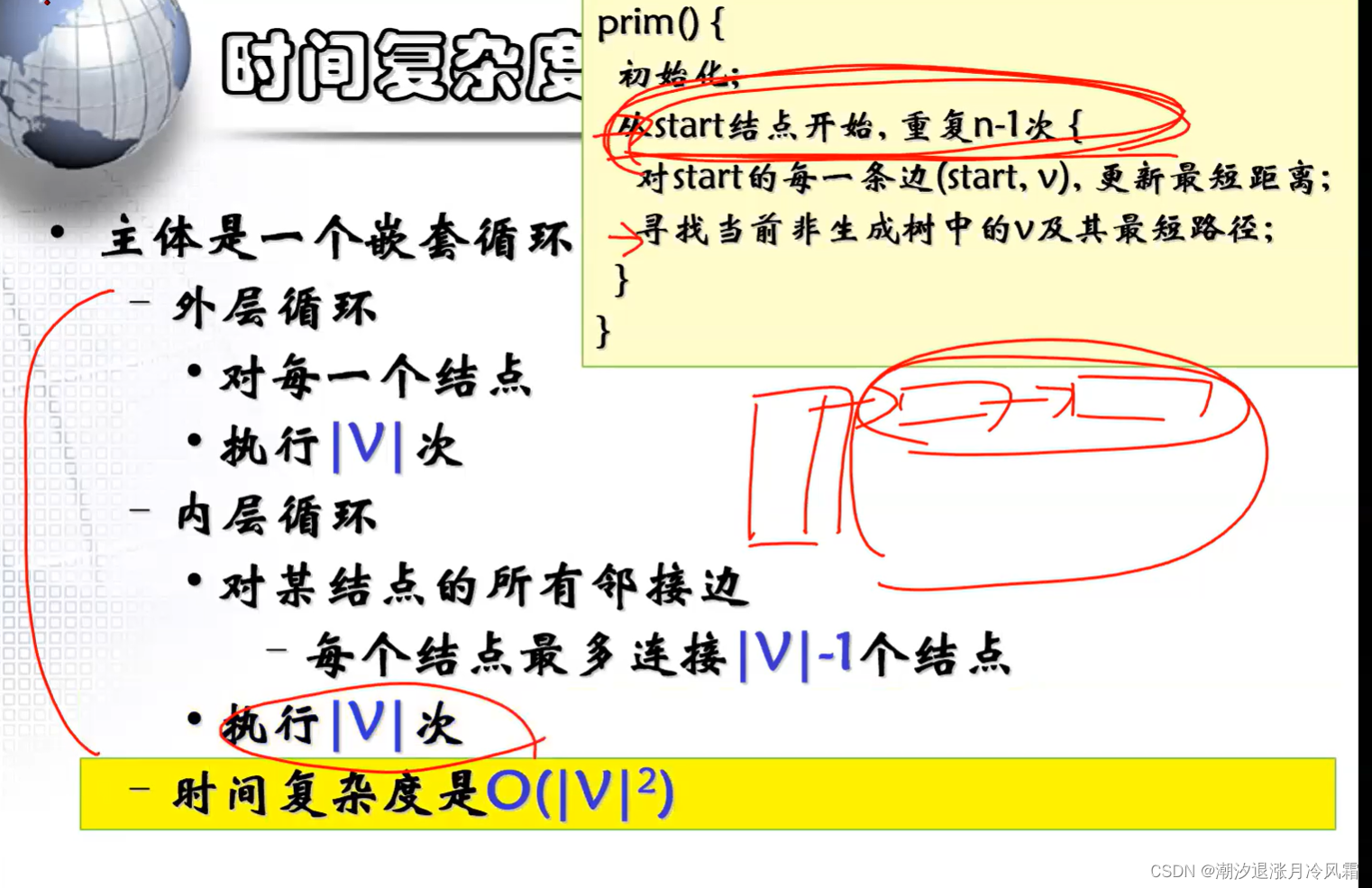

最小生成树不一定唯一,当所有边的权值不同时,最小生成树唯一。
6、最短路径
相关文章:

数据结构——图
一 图论基本概念 Directed Acyclic Graph (DAG) 二 图的存储 ①邻接矩阵(适用于稠密图) ②邻接表(适用于稀疏图) 三、图的遍历 ①深度优先搜索 //(基于邻接表实现,以有向图为例) //DFS:Depth First Search 深度优先搜索 //1、访问起始顶点 …...
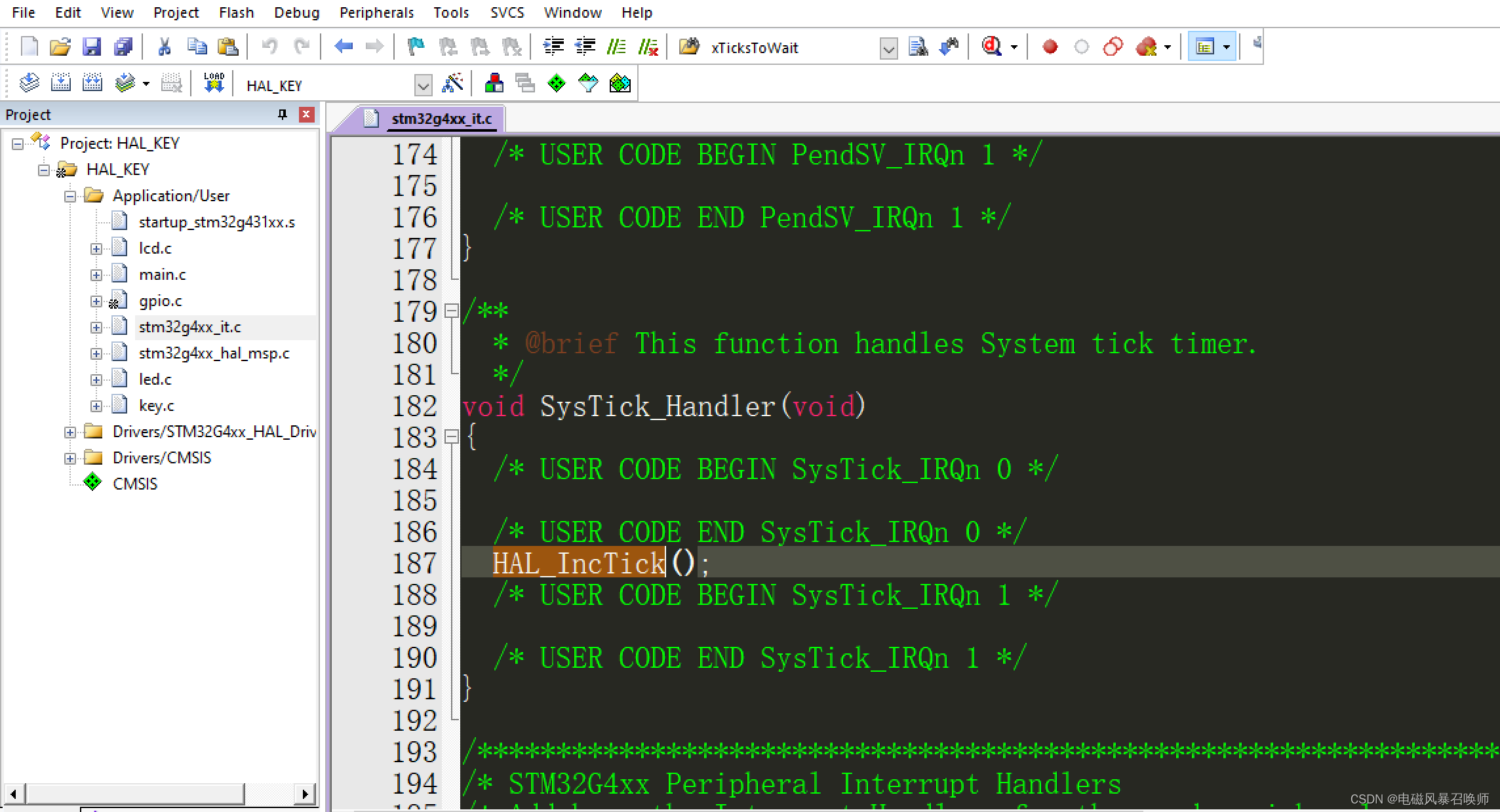
蓝桥杯—SysTick中断精准定时实现闪烁灯
在嵌入式系统中,SysTick_Handler 是一个中断服务例程(Interrupt Service Routine, ISR),用于处理 SysTick 定时器的中断。SysTick 定时器通常用于提供一个周期性的定时中断,可以用来实现延时或者周期性任务。 SysTick…...

ML307R OpenCPU UDP使用
一、UDP通信流程 二、示例 三、UDP通信代码 一、UDP通信流程 ML307R UDP 是使用LWIP的标准的通信,具体UDP流程可以自行百度 二、示例 实验目的:实现把接收的数据再发送到服务端 测试网址:UDP电脑端测试网址 因为是4G,所以必须用外网的 /* 测试前请先补充如下参数 */…...

pod详解
目录 pod pod基本介绍 k8s集群中pod两种使用方式 pause容器使得Pod中所有容器共享两种资源:网络和存储 kubernetes中的pause容器主要为每个容器提供以下功能 k8s设计这样的pod概念和特殊组成结构有什么用意 pod分类 pod容器的分类 基础容器(infr…...

免费插件集-illustrator插件-Ai插件-文本对象分行
文章目录 1.介绍2.安装3.通过窗口>扩展>知了插件4.功能解释5.总结 1.介绍 本文介绍一款免费插件,加强illustrator使用人员工作效率,进行文本对象分行。首先从下载网址下载这款插件 https://download.csdn.net/download/m0_67316550/87890501&…...
)
web学习笔记(五十九)
目录 1.style样式 1.1作用域 scoped 1.2 less和 sass 1.3 less和 sass两者的区别 2. 计算属性computed 3. 响应式基础reactive() 4. 什么是MVVM? 1.style样式 1.1作用域 scoped scoped表示样式作用域,把内部的样式仅限于当前组件模板生效,其…...
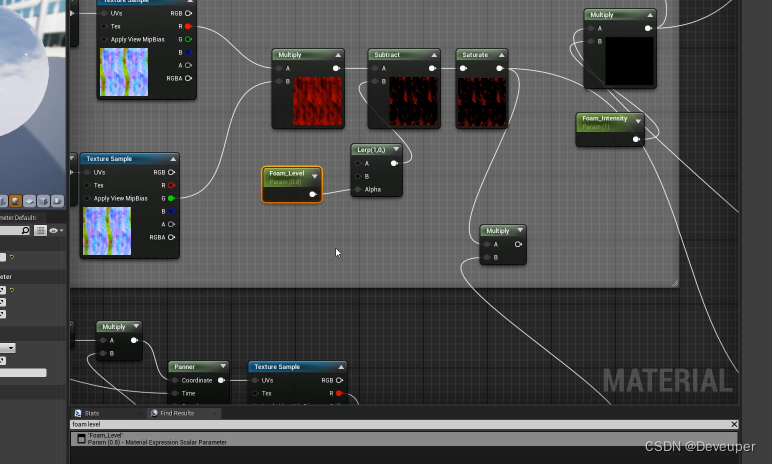
UE5 UE4 快速定位节点位置
在材质面板中,找到之前写的一个节点,想要修改,但是当时写的比较多,想要快速定位到节点位置. 在面板下方的 Find Results面板中,输入所需节点,找结果后双击,就定位到该节点处。 同理,…...
go routing 之 gorilla/mux
1. 背景 继续学习 go 2. 关于 routing 的学习 上一篇 go 用的库是:net/http ,这次我们使用官方的库 github.com/gorilla/mux 来实现 routing。 3. demo示例 package mainimport ("fmt""net/http""github.com/gorilla/mux&…...

新火种AI|警钟长鸣!教唆自杀,威胁人类,破坏生态,AI的“反攻”值得深思...
作者:小岩 编辑:彩云 在昨天的文章中,我们提到了谷歌的AI Overview竟然教唆情绪低迷的网友“从金门大桥跳下去”。很多人觉得,这只是AI 模型的一次错误判断,不会有人真的会因此而照做。但现实就是比小说电影中的桥段…...
AAA实验配置
一、实验目的 掌握AAA本地认证的配置方法 掌握AAA本地授权的配置方法 掌握AAA维护的方法 1.搭建实验拓扑图 2.完成基础配置: 3.使用ping命令测试两台设备的连通性: 二、配置AAA 1.打开R1:配置AAA方案 这两个方框内的可以改名,…...
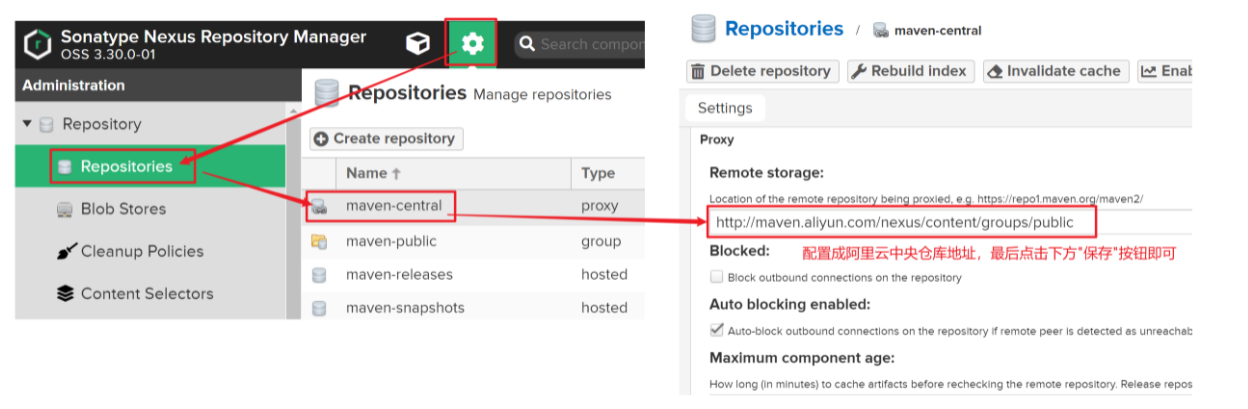
Maven高级详解
文章目录 一、分模块开发与设计分模块开发的意义模块拆分原则 分模块开发(模块拆分)创建Maven模块书写模块代码通过maven指令安装模块到本地仓库(install指令) 二、依赖管理依赖传递可选依赖排除依赖可选依赖和排除依赖的区别 三、聚合与继承聚合工程聚合工程开发创建Maven模块…...

C++的算法:模拟算法
模拟算法是一种基于事物运动变化过程的模型,通过计算机程序来模拟实际系统行为或过程的方法。在C++中,模拟算法常用于解决复杂系统或过程的建模与仿真问题。本文将介绍模拟算法的实现思路及实际应用,并通过具体的实例来展示如何在C++中实现模拟算法。 一、模拟算法的实现思…...

Spring boot集成easy excel
Spring boot集成easy excel 一 查看官网 easyexcel官方网站地址为easyexcel官网,官网的信息比较齐全,可以查看官网使用easyexcel的功能。 二 引入依赖 使用easyexcel,首先要引入easyexcel的maven依赖,具体的版本根据你的需求去…...
【开发 | 环境配置】解决 VSCode 编写 eBPF 程序找不到头文件
问题描述: 在使用 vscode 编写 eBPF 程序时,如果不做一些头文件定位的操作,默认情况下头文件总是带有“红色下划线”,并且大部分的变量不会有提示与补全。 在编写代码文件较小时(或者功能需求小时)并不会…...

View->Bitmap缩放到自定义ViewGroup的任意区域
Bitmap缩放和平移 加载一张Bitmap可能为宽高相同的正方形,也可能为宽高不同的矩形缩放方向可以为中心缩放,左上角缩放,右上角缩放,左下角缩放,右下角缩放Bitmap中心缩放,包含了缩放和平移两个操作…...

十种常用数据分析方法
描述性统计分析(Descriptive Statistics) 使用场景:用来总结数据的基本特征,如平均值、中位数、标准差等。 优势:简单易懂,快速总结数据。 劣势:无法深入挖掘数据的潜在关系。 模拟数据及示例…...
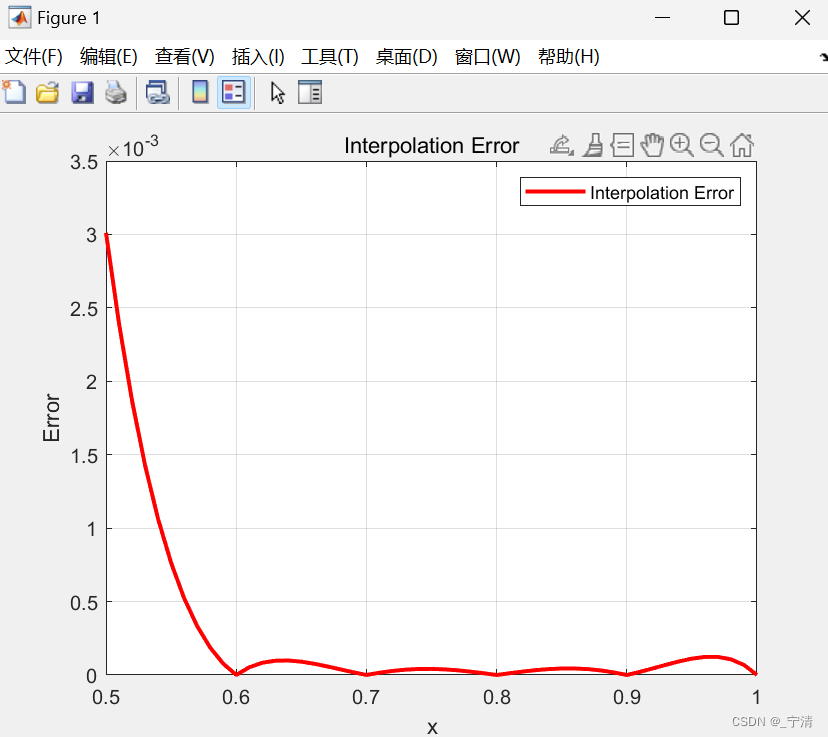
拉格朗日插值及牛顿差商方法的实现(Matlab)
一、问题描述 拉格朗日插值及牛顿差商方法的实现。 二、实验目的 掌握拉格朗日插值和牛顿差商方法的原理,能够编写代码实现两种方法;能够分析多项式插值中的误差。 三、实验内容及要求 利用拉格朗日插值及牛顿差商方法估计1980 年的人口,并…...

【InternLM实战营第二期笔记】02:大模型全链路开源体系与趣味demo
文章目录 00 环境设置01 部署一个 chat 小模型作业一 02 Lagent 运行 InternLM2-chat-7B运行一个工具调用解方程 03 浦语灵笔2进阶作业 第二节课程视频与文档: https://www.bilibili.com/video/BV1AH4y1H78d/ https://github.com/InternLM/Tutorial/blob/camp2/hell…...
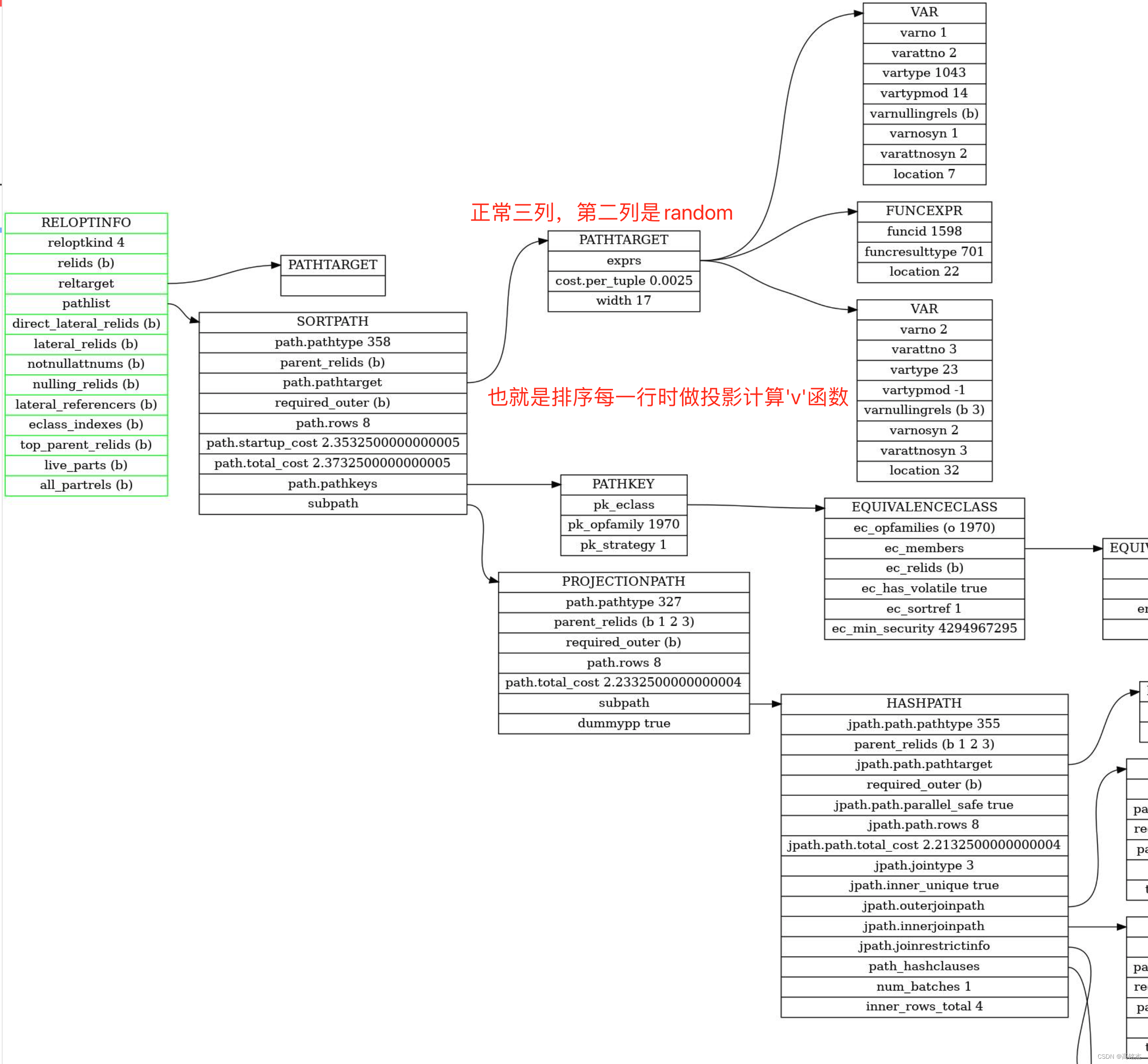
Postgresql源码(134)优化器针对volatile函数的排序优化分析
相关 《Postgresql源码(133)优化器动态规划生成连接路径的实例分析》 上一篇对路径的生成进行了分析,通过make_one_rel最终拿到了一个带着路径的RelOptInfo。本篇针对带volatile函数的排序场景继续分析subquery_planner的后续流程。 subquer…...

DES加密算法笔记
【DES加密算法|密码学|信息安全】https://www.bilibili.com/video/BV1KQ4y127AT?vd_source7ad69e0c2be65c96d9584e19b0202113 根据此视频学习 DES是对称密码中的分组加密算法 (分组加密对应流加密算法) 流加密算法就是一个字节一个字节加密 分组加…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...