LeetCode583:两个字符串的删除操作
题目描述
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。

代码
解法1
/*dp[i][j]:以i-1为结尾的wrod1中有以j-1为尾的word2的个数为了让word1和word2相同,最少操作次数为dp[i][j]递推公式:当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1]; 当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);初始化:dp[i][0] = i, 表示word1不为空,word2为空,需要删除i个元素dp[0][j] = j, 表示word1为空,word2不为空,需要删除j个元素递推公式for(int i=1;i<=word1.size();i++)for(int j=1;j<=word2.size();j++)*/
class Solution {
public:int minDistance(string word1, string word2) {int m = word1.size();int n = word2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (int i = 0; i <= m; i++) dp[i][0] = i;for (int j = 1; j <= n; j++) dp[0][j] = j;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];else dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}return dp[m][n];}
};
解法2:利用最长公共子序列
/*使用最长公共子序列:求出最长公共子序列,然后使用两个字符串分别减去公共就可计算出每个字符串删除的元素return (word1.size()-dp[m][n]) + (word2.size()-dp[m][n])
*/class Solution {
public:int minDistance(string word1, string word2) {int m = word1.size();int n = word2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1[i-1] == word2[j-1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}return (m - dp[m][n]) + (n - dp[m][n]);}
};
相关文章:

LeetCode583:两个字符串的删除操作
题目描述 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 代码 解法1 /*dp[i][j]:以i-1为结尾的wrod1中有以j-1为尾的word2的个数为了让word1和word2相同,最少操作…...
LLama学习记录
学习前: 五大问题: 为什么SwiGLU激活函数能够提升模型性能?RoPE位置编码是什么?怎么用的?还有哪些位置编码方式?GQA(Grouped-Query Attention, GQA)分组查询注意力机制是什么&…...
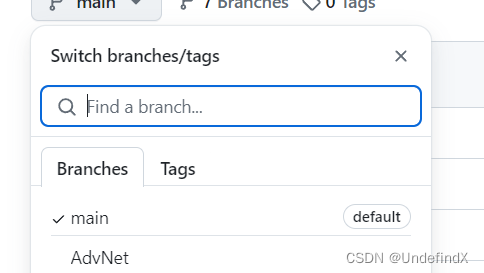
如何克隆非默认分支
直接git clone下来的我们知道是默认分支,那如何克隆其他分支呢: 比如这个,我们想克隆AdvNet。 我们可以在本地文件夹打开Git Bash 依次输入: git clone --branch AdvNet https://github.com/wgcban/SemiCD.git cd SemiCD git b…...

数据结构——图
一 图论基本概念 Directed Acyclic Graph (DAG) 二 图的存储 ①邻接矩阵(适用于稠密图) ②邻接表(适用于稀疏图) 三、图的遍历 ①深度优先搜索 //(基于邻接表实现,以有向图为例) //DFS:Depth First Search 深度优先搜索 //1、访问起始顶点 …...
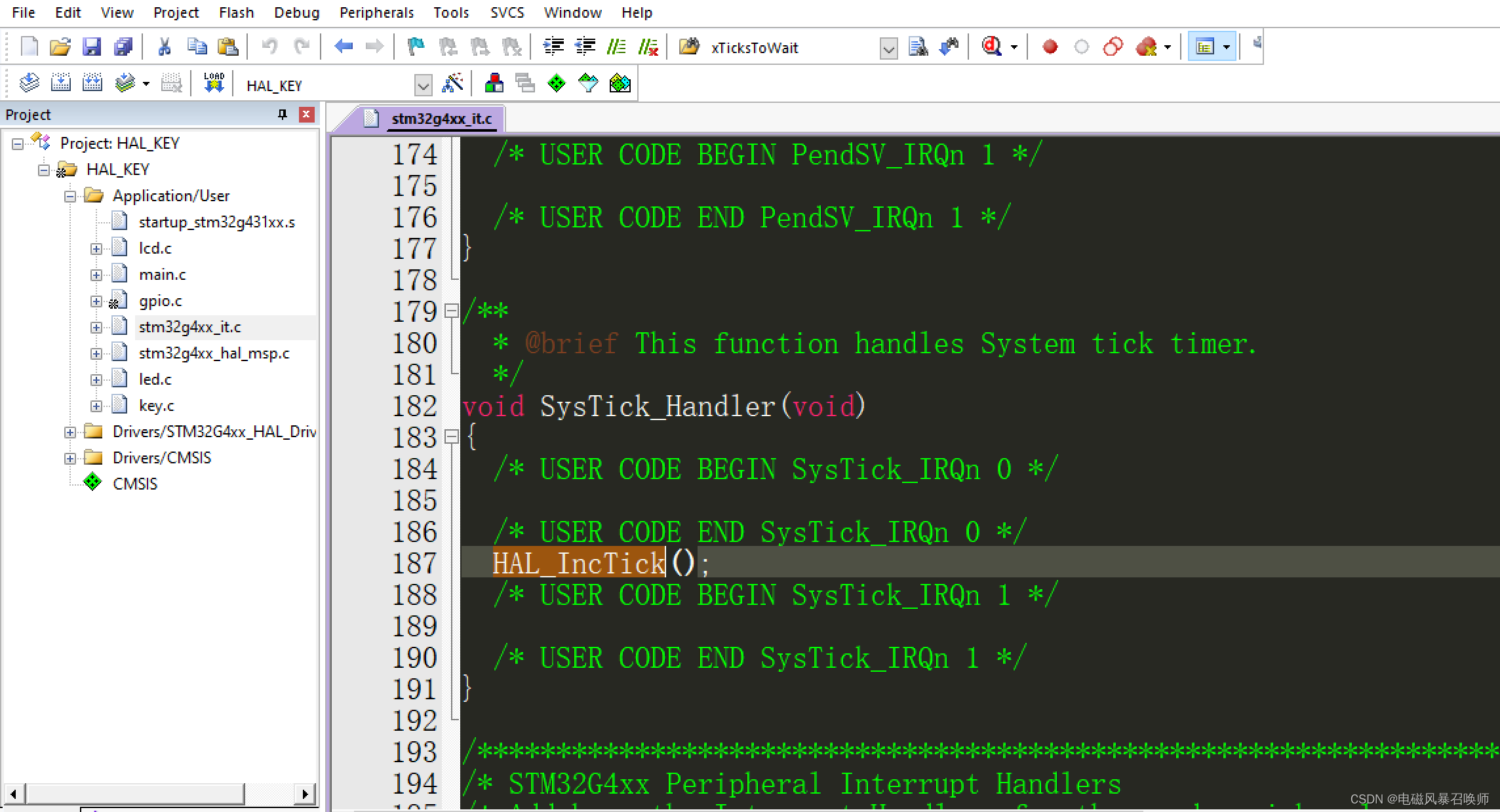
蓝桥杯—SysTick中断精准定时实现闪烁灯
在嵌入式系统中,SysTick_Handler 是一个中断服务例程(Interrupt Service Routine, ISR),用于处理 SysTick 定时器的中断。SysTick 定时器通常用于提供一个周期性的定时中断,可以用来实现延时或者周期性任务。 SysTick…...

ML307R OpenCPU UDP使用
一、UDP通信流程 二、示例 三、UDP通信代码 一、UDP通信流程 ML307R UDP 是使用LWIP的标准的通信,具体UDP流程可以自行百度 二、示例 实验目的:实现把接收的数据再发送到服务端 测试网址:UDP电脑端测试网址 因为是4G,所以必须用外网的 /* 测试前请先补充如下参数 */…...

pod详解
目录 pod pod基本介绍 k8s集群中pod两种使用方式 pause容器使得Pod中所有容器共享两种资源:网络和存储 kubernetes中的pause容器主要为每个容器提供以下功能 k8s设计这样的pod概念和特殊组成结构有什么用意 pod分类 pod容器的分类 基础容器(infr…...

免费插件集-illustrator插件-Ai插件-文本对象分行
文章目录 1.介绍2.安装3.通过窗口>扩展>知了插件4.功能解释5.总结 1.介绍 本文介绍一款免费插件,加强illustrator使用人员工作效率,进行文本对象分行。首先从下载网址下载这款插件 https://download.csdn.net/download/m0_67316550/87890501&…...
)
web学习笔记(五十九)
目录 1.style样式 1.1作用域 scoped 1.2 less和 sass 1.3 less和 sass两者的区别 2. 计算属性computed 3. 响应式基础reactive() 4. 什么是MVVM? 1.style样式 1.1作用域 scoped scoped表示样式作用域,把内部的样式仅限于当前组件模板生效,其…...
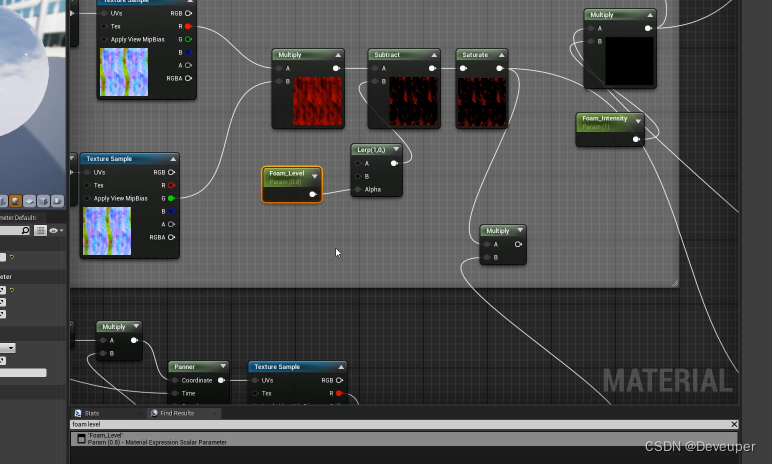
UE5 UE4 快速定位节点位置
在材质面板中,找到之前写的一个节点,想要修改,但是当时写的比较多,想要快速定位到节点位置. 在面板下方的 Find Results面板中,输入所需节点,找结果后双击,就定位到该节点处。 同理,…...
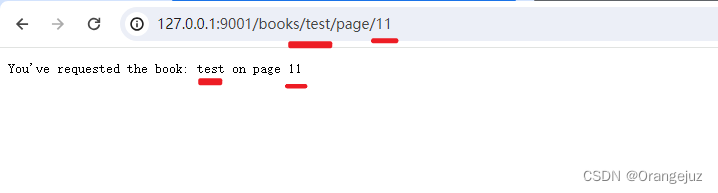
go routing 之 gorilla/mux
1. 背景 继续学习 go 2. 关于 routing 的学习 上一篇 go 用的库是:net/http ,这次我们使用官方的库 github.com/gorilla/mux 来实现 routing。 3. demo示例 package mainimport ("fmt""net/http""github.com/gorilla/mux&…...

新火种AI|警钟长鸣!教唆自杀,威胁人类,破坏生态,AI的“反攻”值得深思...
作者:小岩 编辑:彩云 在昨天的文章中,我们提到了谷歌的AI Overview竟然教唆情绪低迷的网友“从金门大桥跳下去”。很多人觉得,这只是AI 模型的一次错误判断,不会有人真的会因此而照做。但现实就是比小说电影中的桥段…...
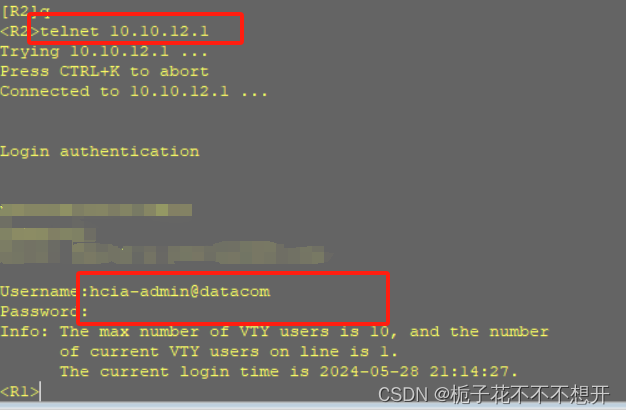
AAA实验配置
一、实验目的 掌握AAA本地认证的配置方法 掌握AAA本地授权的配置方法 掌握AAA维护的方法 1.搭建实验拓扑图 2.完成基础配置: 3.使用ping命令测试两台设备的连通性: 二、配置AAA 1.打开R1:配置AAA方案 这两个方框内的可以改名,…...
Maven高级详解
文章目录 一、分模块开发与设计分模块开发的意义模块拆分原则 分模块开发(模块拆分)创建Maven模块书写模块代码通过maven指令安装模块到本地仓库(install指令) 二、依赖管理依赖传递可选依赖排除依赖可选依赖和排除依赖的区别 三、聚合与继承聚合工程聚合工程开发创建Maven模块…...

C++的算法:模拟算法
模拟算法是一种基于事物运动变化过程的模型,通过计算机程序来模拟实际系统行为或过程的方法。在C++中,模拟算法常用于解决复杂系统或过程的建模与仿真问题。本文将介绍模拟算法的实现思路及实际应用,并通过具体的实例来展示如何在C++中实现模拟算法。 一、模拟算法的实现思…...

Spring boot集成easy excel
Spring boot集成easy excel 一 查看官网 easyexcel官方网站地址为easyexcel官网,官网的信息比较齐全,可以查看官网使用easyexcel的功能。 二 引入依赖 使用easyexcel,首先要引入easyexcel的maven依赖,具体的版本根据你的需求去…...
【开发 | 环境配置】解决 VSCode 编写 eBPF 程序找不到头文件
问题描述: 在使用 vscode 编写 eBPF 程序时,如果不做一些头文件定位的操作,默认情况下头文件总是带有“红色下划线”,并且大部分的变量不会有提示与补全。 在编写代码文件较小时(或者功能需求小时)并不会…...

View->Bitmap缩放到自定义ViewGroup的任意区域
Bitmap缩放和平移 加载一张Bitmap可能为宽高相同的正方形,也可能为宽高不同的矩形缩放方向可以为中心缩放,左上角缩放,右上角缩放,左下角缩放,右下角缩放Bitmap中心缩放,包含了缩放和平移两个操作…...

十种常用数据分析方法
描述性统计分析(Descriptive Statistics) 使用场景:用来总结数据的基本特征,如平均值、中位数、标准差等。 优势:简单易懂,快速总结数据。 劣势:无法深入挖掘数据的潜在关系。 模拟数据及示例…...
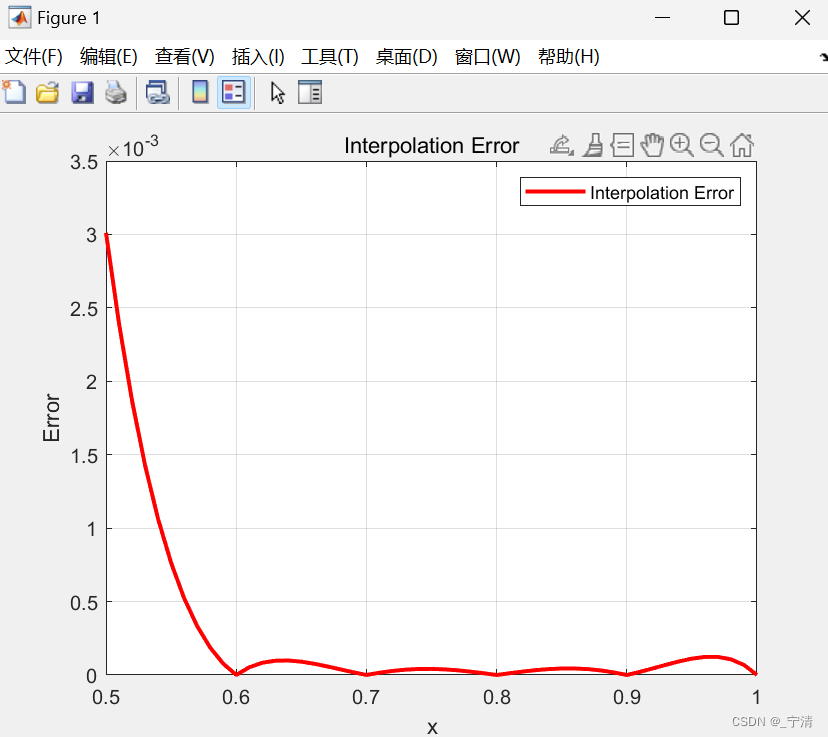
拉格朗日插值及牛顿差商方法的实现(Matlab)
一、问题描述 拉格朗日插值及牛顿差商方法的实现。 二、实验目的 掌握拉格朗日插值和牛顿差商方法的原理,能够编写代码实现两种方法;能够分析多项式插值中的误差。 三、实验内容及要求 利用拉格朗日插值及牛顿差商方法估计1980 年的人口,并…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
