MATLAB分类与判别模型算法：基于Fisher算法的分类程序【含Matlab源码 MX_002期】

算法思路介绍：

费舍尔线性判别分析（Fisher's Linear Discriminant Analysis，简称 LDA），用于将两个类别的数据点进行二分类。以下是代码的整体思路：

1. 生成数据：

   • 使用 randn 函数生成随机数，构建两个类别的合成数据点。
   • 第一个类别的数据点分布在以 (2,2) 为中心的正态分布中。
   • 第二个类别的数据点分布在以 (-2,-2) 为中心的正态分布中。

2. 计算类别均值和散布矩阵：

   • 计算每个类别的数据点的均值（类别中心）。
   • 计算每个类别的散布矩阵（类别内离散度矩阵）。

3. 计算费舍尔线性判别：

   • 计算费舍尔判别向量 W，它是使类间散布与类内散布的比值最大化的向量。
   • 计算类内散布矩阵的总和 Sw。
   • 利用线性代数中的求逆和乘法，计算出判别向量 W。

4. 生成测试样本 (x)：

        使用 randn 函数生成一个随机测试样本。

5. 对测试样本进行分类：

         将测试样本投影到判别向量 W 上，并与预先设定的阈值比较以进行分类。

6. 绘图：

   • 绘制两个类别的数据点，以红色和蓝色表示。
   • 标记测试样本点，并根据分类结果用不同的颜色表示。
   • 绘制费舍尔判别线，表示分类的决策边界。
   • 绘制判别线上的阈值点。
   • 绘制测试样本在判别线上的投影点，并画出测试样本与其投影点之间的连线。

通过这些步骤，代码能够实现费舍尔线性判别分析，并对新的测试样本进行分类和可视化。

部分代码：

m1=mean(X(1:N,:));
m2=mean(X(N+1:2*N,:));
S1=0;S2=0;
for i=1:NS1=S1+(X(i,:)-m1)*(X(i,:)-m1)';
end
for i=N+1:2*NS1=S1+(X(i,:)-m1)*(X(i,:)-m1)';
end
Sw=S1+S2;
W=inv(Sw)*(m1-m2);
W=W./norm(W)
% ====================================================================
x=randn(1,2);%待判样本
y0=W*(m1+m2)'/2;
if W*x'>y0disp('待判样本属于第一类')hold on,plot(x(1),x(2),'r+','MarkerSize',10,'LineWidth',2)
elsedisp('待判样本属于第二类')hold on,plot(x(1),x(2),'b+','MarkerSize',10,'LineWidth',2)
end
legend('Cluster 1','Cluster 2','x','Location','NW')
% =================画投影直线=====================
X1=-8:0.05:8;
X2=(W(2)/W(1))*X1-6;
hold on,plot(X1,X2,'k','LineWidth',2);
% ================求投影直线上的阈值点============
x0=W(1)*(y0)/W(2);
y0=W(2)^2*y0-6*W(1)^2+W(1)*W(2)*x0;
x0=(y0+6)*W(1)/W(2);
hold on,plot(x0,y0,'ro','MarkerSize',10);
% =============求待判样本在投影直线上的投影点==============
y1=W(1)^2*x(1)+6*W(1)*W(2)+W(1)*W(2)*x(2);
y2=W(2)/W(1)*y1-6;
hold on,plot(y1,y2,'r.','MarkerSize',30);
hold on,plot([x(1) y1],[x(2) y2],'g','LineWidth',2);

结果展示：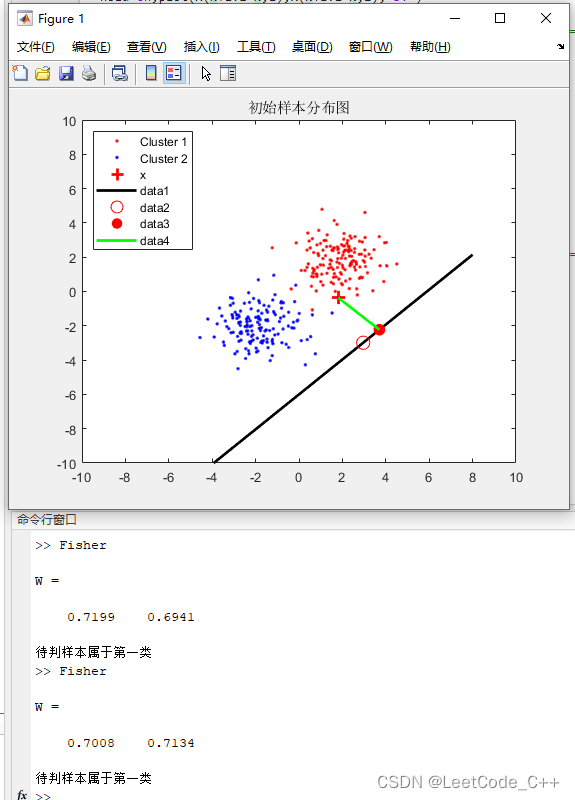

获取代码：MATLAB分类与判别模型算法：基于Fisher算法的分类程序